【最优化】凸函数的驻点是全局最优点
由small_q创建,最终由small_q 被浏览 141 用户
定理
首先我们来看定理:设f(x): Rn→R 为可微凸函数,如果 x∗∈R是驻点,那么 x∗ 为f的最优点(global.opt)。
换句话说就是,如果函数是凸函数,那么该函数的驻点就是全局最优点。
下面来证明一下:
要判断一个点是全局最小值的话,比如 x∗ 是全局最小值,那么该函数的其他任意点都会比驻点的函数值大,满足: ∀x,f(x)≥f(x∗)。
也就是说,我们来证明上面这个公式成立即可。
证明
由凸函数的一阶特征可得下面结论:【最优化】凸函数及它的一阶特征
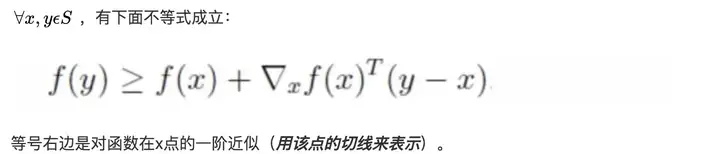
其中我们将令上述的 y=x,x=x∗ ,又因为 x∗ 是驻点,则 x∗ 的一阶导数为0.
推导
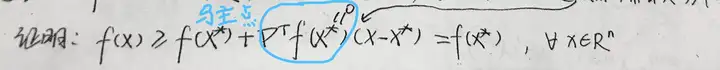
所以我们推出了对于任意的x,都满足 ∀x,f(x)≥f(x∗) ,则证明了凸函数的驻点是全局最优点