【最优化】凸函数及它的一阶特征
由small_q创建,最终由qxiao 被浏览 170 用户
什么是凸函数

直观的,图1是一维凸函数的示例。一维情况下,不严格的说,凸函数是弦在上的函数或者是曲线向上包(这些都是不严谨的说法)。
注意:在不同的教科书和资料中,对凸函数的定义有可能是相反的,在机器学习领域,一般都使用这个定义。
凸函数的一阶特征
设 SϵRn 为非空开凸集, f 满足一阶连续可导,并且是S上的凸函数,则满足下面充要条件:
∀x,yϵS ,有下面不等式成立:
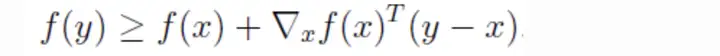
等号右边是对函数在x点的一阶近似(用该点的切线来表示)。
凸函数的一阶特征的几何意义
一阶条件的意义是,对于函数在定义域的任意取值,函数的值都大于或者等于对函数在这点的一阶近似。用图来说明就是下方图:
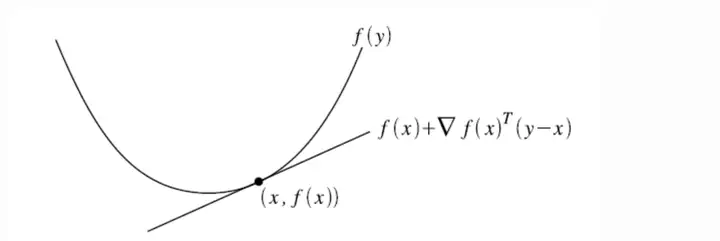
比如说,在下方的无论是A点还是B点,还是这个函数上的任意一点,函数的值都大于或者等于函数在这点的一阶近似(切线近似)
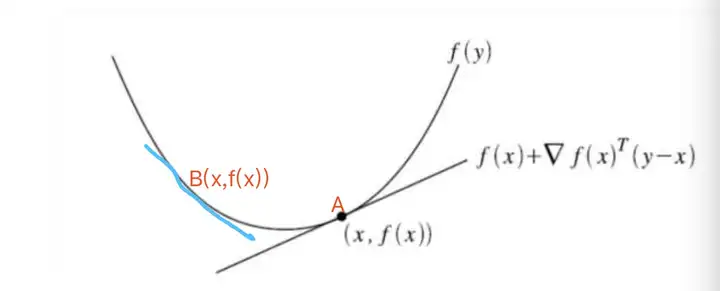
这也就是凸函数的一阶特征的几何意义。
通过图可以很清楚地理解这个充要条件,但是,具体在应用中,我们不可能对每一个点都去计算函数的一阶导数,因此后面会说道利用凸函数的二阶特征来进行判断一个函数是否是一个凸函数。
凸函数的一阶特征的证明
好了,其实到第三部分,就已经对凸函数的一阶特征就做了详细的介绍了,这里再对它进行证明(下面来自德川的课堂笔记,我做了一点注解):
