什么是无监督学习(机器学习)
由qxiao创建,最终由qxiao 被浏览 259 用户
什么是无监督学习?
顾名思义,“无监督”学习发生在没有监督者或老师并且学习者自己学习的情况下。
例如,考虑一个第一次看到并品尝到苹果的孩子。她记录了水果的颜色、质地、味道和气味。下次她看到一个苹果时,她就知道这个苹果和之前的苹果是相似的物体,因为它们具有非常相似的特征。她知道这和橙子很不一样。但是,她仍然不知道它在人类语言中的名称是什么,即“苹果”,因为不知道这个标签。
这种不存在标签(在没有老师的情况下)但学习者仍然可以自己学习模式的学习称为无监督学习。

在机器学习算法的上下文中,当算法从没有任何相关响应的普通示例中学习并自行确定数据模式时,就会发生无监督学习。
在下一节中,我们将讨论这种类型的学习与机器学习中其他类型的流行学习算法(即监督学习算法)有何不同。
监督学习与无监督学习
顾名思义,监督学习中的学习是在监督下进行的,即当算法从训练数据中预测样本的值时,它会被告知预测是否正确。
这是可能的,因为我们将正确的值存储为“标签”/“目标变量”,这些值与输入数据一起传递给算法。常见的监督学习任务是分类和回归。
在分类任务中,标签是样本所属的正确类别,而在回归中,因变量 (Y) 的实际值用作比较预测的基准。然后,该算法可以调整其参数以实现更高的预测准确度。
因此,监督学习的主要目标是建立一个稳健的预测模型。
另一方面,在无监督学习中,我们只传递输入数据,没有标签。无监督模型试图找到数据中的底层或隐藏结构或分布,以便更多地了解数据。
换句话说,无监督学习是我们只有输入数据而没有相应的输出变量,主要目标是从输入数据本身中学习更多或发现新的见解。
无监督算法的一个常见示例是聚类算法,它根据机器检测到的模式对数据进行分组。
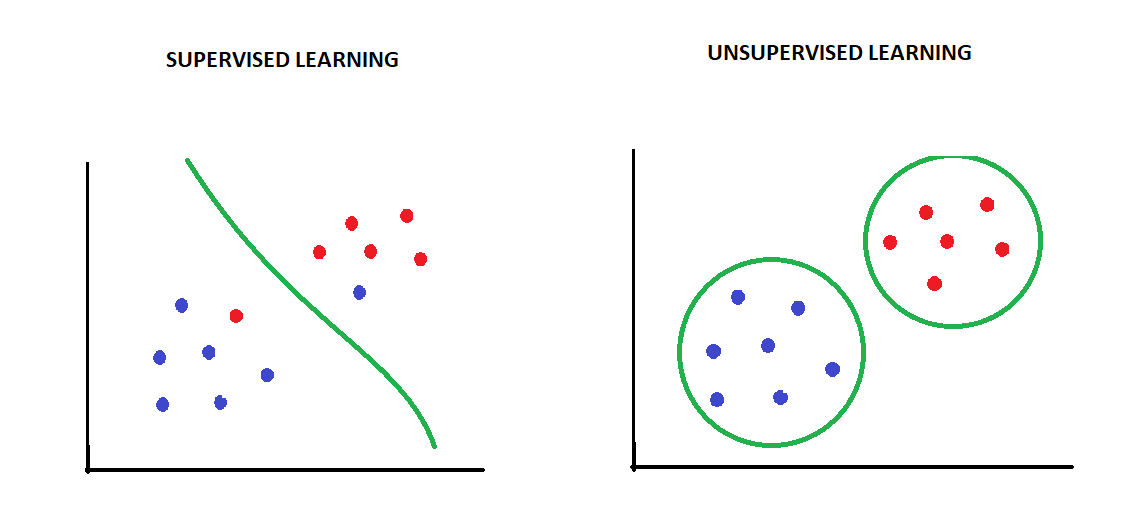
例如,让我们考虑一个基于两个输入特征 X1 和 X2 的数据点的情况。
- 如果我们希望我们的算法将数据分类/分类为两个已知类别,我们将使用监督分类算法。
- 另一方面,如果我们希望算法告诉我们数据的结构,我们将使用无监督聚类算法。
我们什么时候使用无监督算法?
在以下条件下使用无监督学习:
- 我们没有输出/目标数据。
- 我们并不完全知道我们在寻找什么,并希望机器发现数据中的模式/洞察力。然后,机器发现的见解可用于解决各种挑战。
- 我们只想从数据中过滤掉基本信息(与原始数据相比具有较低的维度),并仅使用它来训练监督学习模型。
在接下来的两节中,我们将研究两种流行的无监督算法,即聚类和降维,它们在这些情况下对我们有帮助。
聚类算法
聚类的概念
聚类是无监督学习领域中最流行的任务之一。在这里,基本假设是相似的数据点往往属于相似的组(称为集群),这取决于它们与局部质心的距离。
因此,不是在查看数据之前定义组,聚类允许我们找到和分析有机形成的组,即基于数据本身。
有不同的聚类算法,如 K-means 聚类、层次聚类、DBSCAN、OPTICS 等,它们根据自己对数据点之间相似性的定义对数据进行分组。
在下一小节中,我们将看一个 K-means 聚类的示例,它是一种广泛使用的聚类算法。它创建了“K”个类似的数据点集群。
K-means 聚类算法
当我们有未标记的数据(即没有定义的类别或组的数据)时,使用 K-means 聚类。该算法在数据中查找组/簇,组数由变量“k”(因此得名)表示。
该算法迭代地工作以根据所提供特征的相似性将每个观察分配给 k 个组之一。
K-means 算法的输入是数据/特征(Xis)和“K”的值(要形成的簇数)。
步骤可以概括为:
- 该算法从随机选择“K”个数据点作为“质心”开始,其中每个质心定义一个集群。
- 在此步骤中,将每个数据点分配给由质心定义的集群,以使该数据点与集群质心之间的距离最小。
- 在这一步中,通过取上一步中分配给该集群的所有数据点的平均值来重新计算质心。
该算法在步骤 (ii) 和 (iii) 之间迭代,直到满足停止标准,例如达到预定义的最大迭代次数或数据点停止更改集群。
使用 Python 代码进行交易或投资的 K-means 聚类示例
通常,交易者和投资者希望根据某些特征的相似性对股票进行分组。
例如,希望交易配对交易策略的交易者同时持有两只相似股票的多头和空头头寸,理想情况下希望扫描所有股票并找到在行业方面彼此相似的股票,部门、市值、波动性或任何其他特征。
现在考虑一个场景,交易者根据两个特征对 12 家美国公司的股票进行分组/聚类:
- 股本回报率 (ROE) = 净收入/股东权益总额,以及
- 股票的贝塔
投资者和交易者使用 ROE 来衡量公司相对于股东权益的盈利能力。当然,高 ROE 更适合投资一家公司。另一方面,Beta 代表股票相对于整体市场的波动性(以标准普尔 500 或道琼斯指数等指数为代表)。
手动检查每一个库存然后形成组是一个乏味且耗时的过程。相反,可以使用聚类算法(例如 k-means 聚类算法)根据给定的一组特征对股票进行分组/聚类。
下面,我们实现了一个 K-means 算法,用于在 Python 中对这些股票进行聚类。我们首先使用以下命令导入必要的库并获取所需的数据:
下载:ADBE
下载:AEP
下载:CSCO
下载:EXC
下载:FB
下载:GOOGL
下载:INTC
下载:LNT
下载:微软
下载:STLD
下载:TMUS
下载:XEL
如下所示,获取了所有 14 个代码的数据,因此 bad_tickers 列表为空:
[]
现在让我们看看我们的数据:
如上所示,我们已经成功下载了 12 只股票的数据。
我们现在将创建原始数据的副本(df)并使用它。第一步是对数据进行预处理,以便将其提供给 k-means 聚类算法。这涉及将数据转换为 NumPy 数组格式并对其进行缩放。
缩放相当于从该列中的每个数据点减去列平均值并除以列标准偏差。
对于缩放,我们使用 scikit-learn 库的 StandardScaler 类,如下所示:
[[ 1.48101786 0.53827712]
[-1.02433415 -1.29230095]
[0.25330094 0.40752155]
[-1.25368786 -0.82158087]
[0.58249097 1.45356616]
[-0.36055752 0.72133493]
[0.79700415 -0.37701191]
[-0.93933836 -1.08309203]
[ 1.80211305 0.11985928]
[0.46916325 1.92428624]
[-0.7733942 -0.42931414]
[-1.03377812 -1.16154537]]
下一步是从 scikit learn 导入“KMeans”类,并拟合一个模型,其中超参数“K”的值(在 scikit learn 中称为 n_clusters)设置为 2(随机选择),我们将预处理数据拟合到该模型中。 df_values':
而已!'km_model' 现在已经训练好了,我们可以提取它分配给每只股票的集群,如下所示:
现在我们已经分配了集群,我们将使用 matplotlib 和 seaborn 库将它们可视化,如下所示:
我们可以清楚地看到 K-means 算法分配给数据点的两个集群之间的差异。集群 1 主要由所有公用事业公司组成,与集群 0 中的高增长科技公司相比,这些公用事业公司的 ROE 和贝塔值较低。
虽然我们没有告诉 K-means 算法这些股票所属的行业,但它是能够在数据本身中发现该结构。这就是无监督学习的力量和吸引力。
接下来出现的问题是如何在拟合模型之前确定超参数 K 的值?
我们在拟合模型时随机传递了超参数 K = 2 的值。这样做的一种方法是检查模型的“惯性”,它表示群集中的点与其质心的距离。
随着越来越多的集群被添加,惯性不断减少,形成了所谓的“弯头曲线”。我们选择 k 的值,超过该值我们看不到惯性值有多大好处(即减少)。
下面我们绘制了具有不同“K”值的 K 均值模型的惯性值:
我们可以看到,在 k=3 之后,惯性值显示出边际递减,k=3(三个集群)的 k-means 模型最适合这项任务。
降维
降维的概念
维度灾难是数据科学家和量化专家面临的一个常见问题,这意味着使用过多的特征可能会不必要地增加 ML 模型的存储空间和处理时间。因此,我们总是寻求在不丢失太多信息的情况下在较低维度上获得有用的数据表示。
这是通过使用降维技术来实现的,这是无监督学习的另一个流行用例。
降维将导致在速度和内存使用方面的高性能,但会丢失一些信息。我们需要确保收益超过丢失该信息的成本。
在下一节中,我们将介绍 PCA,它是最流行的无监督降维技术。
主要成分分析
减少数据维度的一种直观方法是将数据点投影到较低的子空间,如下图所示,我们将点从 3-D 空间(三个特征 x1、x2 和 x3)投影到 2 -D 子空间(只有 x1 和 x2):
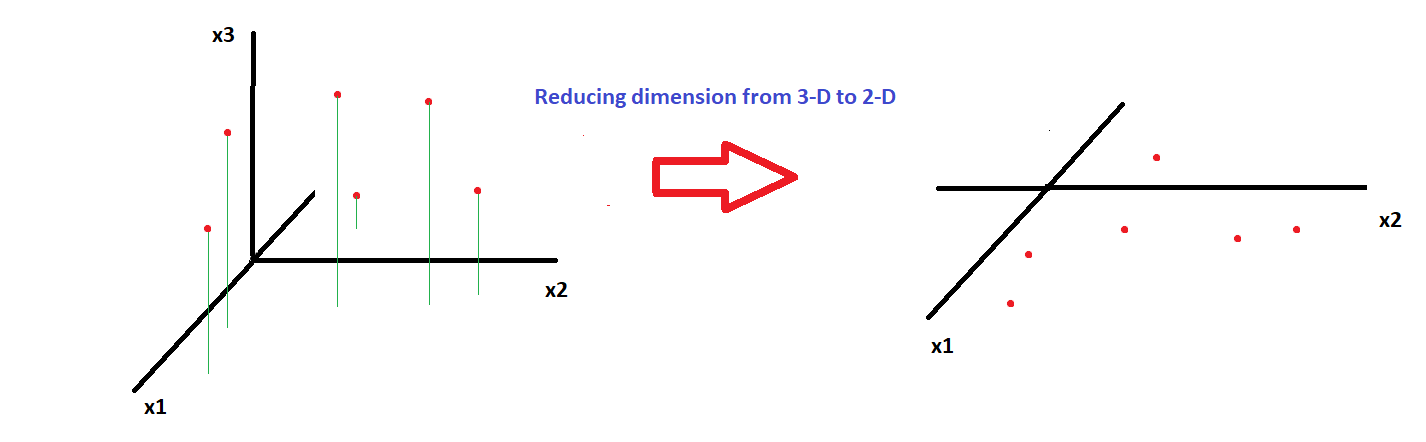
主成分分析 (PCA) 使用相同的方法;然而,在 PCA 中,我们找到了解释数据最大变化的新坐标。这是通过以下方式实现的:
- 首先意味着使数据居中,即使每列的平均值为0,然后
- 找到以均值为中心的变量的协方差矩阵(C) 的特征分解。方阵(协方差矩阵总是方阵)的特征分解由下式给出:
C = V.Λ.V T
这里“V”表示包含特征向量(协方差矩阵 C)的矩阵,它表示我们的新坐标或主成分,Λ 是包含 C 的特征值的对角矩阵。
Λ 中的每个对角线值都是一个特征值,表示相应主成分解释的方差。此过程确保生成的新坐标/特征/主要组件旨在捕获数据中的最大变化并且彼此正交(垂直)(即,我们的新特征彼此不相关)。
下一步是我们根据预先确定的截止值选择前几个主成分(依次解释最大变化)。
例如,如果我们一开始有五个特征,我们最终也会有五个主成分,但我们决定只保留前三个,因为它们解释了数据中 90% 的变化。这实际上意味着我们将特征空间的维度从 5 减少到 3,而不会丢失太多信息。
在下一小节中,我们将看一个在交易中实施 PCA 的示例。
使用 Python 代码进行交易或投资的 PCA 示例
假设在一家自营贸易公司工作的量化研究员 Jim 正在寻求开发一个有监督的 ML 模型来预测整个市场的方向。他决定使用一篮子 7 只科技股的过去一天的回报(假设它们与前面示例中属于集群 0 的股票相同)作为模型的特征。
为了更有效地利用资源,Jim 想要在将特征输入到他的监督模型之前减少他的特征空间的维度。
*什么可以帮助他在这里快速探索减少手头数据维度的可能性? *是的,你是对的,它是 PCA!
下面我们将展示 Jim 如何使用 Python 中的 scikit learn 包进行 PCA。
但首先,我们导入必要的库并获取数据,如下所示:
['ADBE'、'CSCO'、'FB'、'GOOGL'、'INTC'、'MSFT'、'STLD']
下面,我们绘制股票的累积回报来衡量表现以及数据的变化:
PCA 的第一步是对数据进行均值中心化。但是,我们将使用 scikit-learn 库中的 PCA 类,它会自动缩放数据(意味着居中),因此无需手动进行(如果您使用其他包,那么您可能有自己通过矩阵运算或使用 sklearn. 进行预处理,如聚类示例中所做的那样)。
我们将根据 scikit learn 库的要求将数据简单地转换为 NumPy 数组格式,导入 PCA 类并创建一个名为“模型”的实例,我们将在其中拟合原始数据 X:
PCA(n_components=7)
模型“n_components”的超参数表示新坐标/主成分空间的维度。
首先,我们将模型初始化为超参数“n_components”的值设置为 7,这与 X 中的原始特征数量相同(因为我们有 7 个股票)。
我们可以使用以下命令访问主成分矩阵/特征向量矩阵:
数组([[ 0.43250364, 0.26595616, 0.43994419, 0.39167868, 0.39734818,
0.37164424, 0.31502354],
[ 0.31078208,-0.1784099,0.31343949,0.10492004,-0.16196493,
0.17032255,-0.84088612],
[ 0.07033748,-0.13062127,0.35532243,0.14605034,-0.83342892,
0.01607169, 0.3681629],
[-0.32754799, -0.62923875, 0.52613624, 0.06641712, 0.34086264,
-0.30207809, 0.09001009],
[ 0.23384309,-0.65419348,-0.5269365,0.33600016,0.0217246,
0.32947421, 0.13328505],
[-0.58953337,0.22761183,-0.08110947,0.7444334,-0.0673928,
0.05821513,-0.178753],
[-0.44931934,-0.06824695,0.14453582,-0.37783656,-0.00877099,
0.79335935, 0.01753355]])
上面的主成分已经自动按照它们解释的方差顺序排列(从高到低)。所以现在,我们实际上可以提取并绘制每个主成分捕获的方差百分比,如下所示:
数组([0.51, 0.21, 0.12, 0.06, 0.05, 0.03, 0.02])
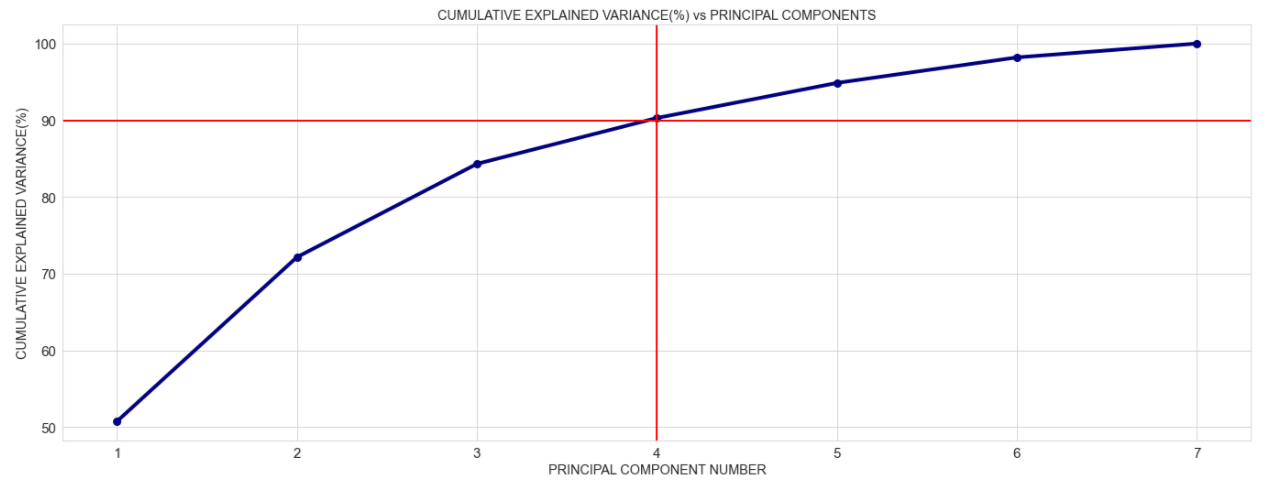
接下来,我们将解释的累积方差可视化:
我们可以在上面看到前 4 个主成分解释了几乎 90% 的方差!
这意味着 Jim 只能使用具有 4 个主成分的 PCA 模型,以不解释数据中 10% 的方差为代价将维度从 7 减少到 4。听起来很划算!
下面,我们用 'n_components' = 4 拟合一个新的 PCA 模型,并将其称为 'model_2':
我们现在可以访问主成分和连续主成分解释的变异百分比:
数组([[ 0.43250364, 0.26595616, 0.43994419, 0.39167868, 0.39734818,
0.37164424, 0.31502354],
[ 0.31078208,-0.1784099,0.31343949,0.10492004,-0.16196493,
0.17032255,-0.84088612],
[ 0.07033748,-0.13062127,0.35532243,0.14605034,-0.83342892,
0.01607169, 0.3681629],
[-0.32754799, -0.62923875, 0.52613624, 0.06641712, 0.34086264,
-0.30207809, 0.09001009]])
数组([0.5074455,0.21408255,0.12162805,0.05979477])
最后,我们可以访问我们的新特征(Z),它对应于投影在主成分空间中的原始数据 X:
数组([[-1.12727573e-01,-6.67038416e-03,-1.48430796e-03,
1.14035934e-03],
[ 2.97074556e-02、1.50265487e-02、-5.93081631e-02、
-2.99243627e-02],
[-5.47331714e-02,-4.75781399e-03,-1.65305232e-02,
7.99569198e-03],
...,
[-1.09056976e-02,-8.34552109e-05,1.17423510e-02,
-2.00353992e-03],
[-4.17360862e-03、2.44548028e-03、1.19544647e-02、
1.89425233e-02],
[ 3.66918890e-02、1.94108416e-02、1.62907120e-02、
4.10635097e-02]])
让我们看一下原始数据和降维数据的形状:
(272, 7)
(272, 4)
查看原始数据的形状和新的降维数据,我们可以看到像 PCA 这样的无监督学习算法如何帮助我们更有效地利用资源并创建新特征来构建简约的监督模型。
这就是吉姆想要的!他现在可以愉快地继续使用这些新功能构建他的监督模型。
其他类型的无监督算法
在前两节中,我们讨论了两种最流行的无监督算法类型,即聚类和降维算法。除此之外,还有其他类型的无监督学习算法,用于特定目的。
一个有用的实现是潜在变量建模。潜在变量是不能直接观察到但对其他一些观察到的变量有影响的变量。
无监督学习可用于了解观察变量中的结构和模式,从而对潜在变量进行建模。一个很好的例子是隐马尔可夫模型,它可以用来检测金融市场背景下的市场制度。
无监督学习的另一个常见用例是关联规则学习。这里的目的是挖掘大量数据并发现特征之间的有用关系。
例如,超市公司可以部署这种类型的分析来分析顾客的购物篮,看看哪些商品可能会一起购买。该公司可以将这些物品彼此相邻放置(例如,将黄油和奶酪放在面包区旁边)以提高销售量。
无监督学习的挑战
尽管我们已经看到无监督学习如何帮助我们学习输入数据中的模式,但它也有其自身的挑战:
- 由于无监督学习中没有标签/目标变量,因此没有像我们在监督学习算法中那样计算模型性能的固定方法。
- 用户通常必须花费大量时间来解释输出。例如,从 PCA 获得的新特性需要在业务上下文中进行解释,而这本身就需要时间。
这就是为什么无监督学习经常与监督学习结合使用的原因。
结论
在本博客的过程中,我们看到了无监督学习算法如何不仅为我们提供对输入数据的洞察,而且还为有监督的机器学习算法提供了新的有用输入。
\