量化交易之时间序列数据的分析和预测

由small_q创建，最终由qxiao更新于2024-06-11 02:46 被浏览 395 用户

什么是时间序列和时间序列分析

时间序列是随时间推移的一系列观察结果，用于所描述现象随时间变化的情况。这类数据反映了某一事物、现象等随时间的变化状态或程度。比如以下都是时间序列数据的例子“

• 过去 5 年的每日股价
• 过去 90 天的 1 分钟股价数据
• 一家公司过去 10 年的季度收入
• 一家汽车制造商过去 3 年的月度汽车销量
• 一个州过去 50 年的年失业率

来到时间序列分析，它只是意味着识别那些有助于分析时间序列数据的方法。

由于预测股票市场的未来股票价格对投资者至关重要，时间序列及其相关概念具有组织数据以进行准确预测的卓越品质。在本文中，让我们阅读时间序列的重要性、分析和预测。

时间序列分析的主要目的是开发能够最好地捕捉或描述时间序列或数据集的模型。此外，这有助于了解数据集的根本原因，以帮助您创建有意义且准确的预测。

此外，我们将在未来看到几种类型的时间序列。

时间序列的类型

现在让我们看看数据集可以属于的时间序列类型：

• 单变量和多变量
• \

单变量和多变量

单变量时间序列是指单个变量随时间变化的一组观察值。这里要注意的重要一点是，这种类型总是将时间作为隐式变量。而且，如果数据点是等距的，则不需要明确给出时间变量。此类型可帮助您确定因变量（价格值）在时间方面的差异，即自变量。

例如，A公司过去两年的股票价格数据，每年每个月的股票价格都会被提及。在这里，让我们假设 12 月和 1 月的股票价格处于特定范围内。

现在，每当我们需要预测未来的股价时，我们都会查看过去的数据。这将告诉我们，明年和随后的几年，12 月和 1 月的股票价格可能处于该特定范围内。而且，基于此，您也许可以做出交易决定。

通过这种方式，您可以提取过去多年的数据，并找出依赖于时间的变量在这些年中的表现，从而正确预测未来。

在这个例子中，我们只使用了一个变量，即“股票价格”，它取决于时间。

伟大的！更进一步，还有另一种类型，称为多变量。现在让我们看看什么是多元时间序列。

多变量时间序列是指多个变量而不是一个变量随时间变化的一组观察值。在这种类型中，每个变量不仅取决于一种类型的等距数据，而且还取决于除此之外的其他变量。

例如，同一家公司 A 的股票价格不仅取决于每年每个月设定的时间，还取决于时尚趋势、场合等其他变量。

现在，这样一个依赖于许多其他变量的变量（股票价格）如何帮助您预测未来的股票价格？

为此，您必须考虑观察到的变量所依赖的每个变量，并且基于该研究，您还可以预测未来的股票价格。

让我们继续看看平稳和非平稳时间序列。

平稳和非平稳时间序列

平稳时间序列

定义一个平稳时间序列，它是一个均值和方差随时间保持不变的序列。换句话说，它的属性不依赖于观察系列的时间。因此，时间序列是一个没有趋势的平坦序列，随时间变化恒定，均值恒定，自相关恒定且没有季节性。这使得平稳时间序列易于预测。

非平稳

非平稳时间序列是指均值或方差或两者都随时间不恒定的序列。

有不同的测试可用于检查给定的时间序列是否是平稳的：

• 自相关函数 (ACF) 测试
• 偏自相关函数 (PACF) 检验

自相关函数 (ACF) 测试 – 自相关函数检查时间序列的两个不同数据点之间的相关性，这些数据点之间用滞后“h”分隔。例如，ACF 将检查点 #1 和 #2、#2 和 #3 等之间的相关性。类似地，对于滞后 3，ACF 函数将检查点 #1 和 #4、#2 和 #5、# 3和#6等。

自相关函数测试主要用于两个原因：

• 用于检测数据中的非随机性和
• 用于识别特定数据集的适当时间序列模型。

因此，自相关函数测试对于提供准确的结果很重要。

ACF 的 Python 代码-

运行上面的 python 代码后，您将获得前 20 个滞后的自相关的 2D 图：

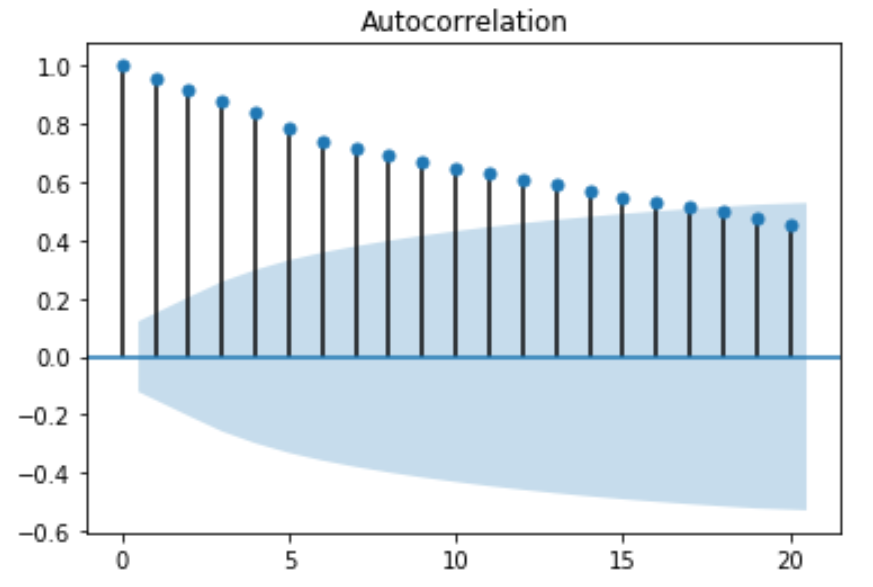
偏自相关函数 (PACF) – 在某些情况下，较小滞后的自相关效应将对较长滞后的自相关估计产生影响。例如，强滞后一号可能导致与滞后三号的自相关。偏自相关函数 (PACF) 从较长滞后的相关估计中消除较短滞后自相关的影响。

PACF 的 Python 代码-

运行上面的代码会为前 20 个滞后带来具有部分自相关的数据的 2D 表示：

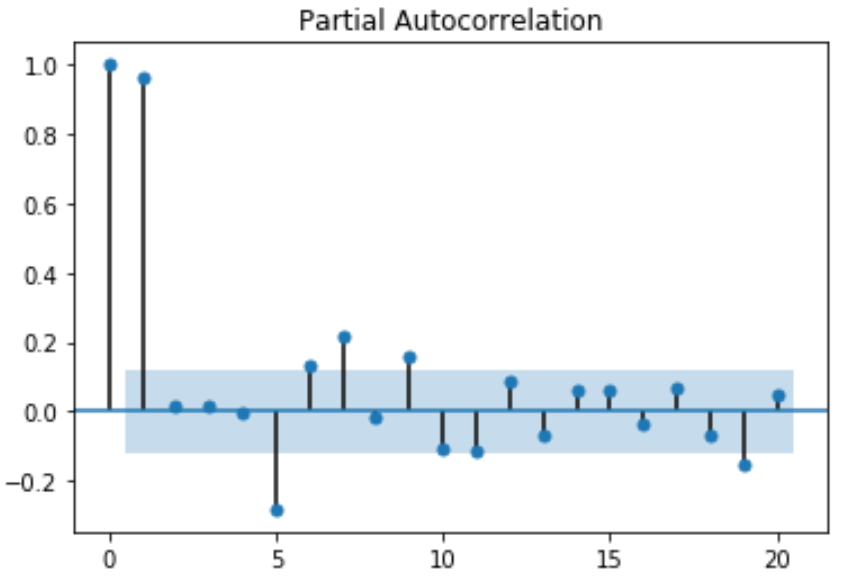
ACF 和 PACF 的值在正负一之间变化。当值接近正负一时，表明相关性强。此外，需要注意的是，如果时间序列是平稳的，则 ACF 会相对较快地下降到零。而非平稳时间序列的 ACF 将缓慢下降。此外，通过 ACF 图，我们可以得出结论，给定的时间序列是非平稳的。

现在好了！让我们探索一下 ACF 和 PACF 之间的一些区别，以便于理解：

好吧！让我们进一步了解时间序列分析的组成部分，这些组成部分对于理解时间序列中的不同点是不可或缺的。

时间序列分析的组成部分是什么？

基本上，时间序列分析采用时间序列的整个数据集，可以分为三个部分。这些组件根据每个值的性质将整个数据集划分为不同的类别。因此，时间序列的三个组成部分被隔离为：

• 趋势 - 给定时间序列中增加或减少值的连续性。
• 季节性 - 给定时间序列中特定时间段（日、周、月等）的重复周期。
• 不规则或随机不规则（噪声） - 给定时间序列中值的随机不规则。

这里要注意的另一个有趣的点是，将时间序列分离为所有这些组件也称为分解。正如我们所提到的，时间序列可能包括季节性成分或不规则成分。因此，当时间序列发生分离时，各种模式被清晰地分离出来，这有助于根据每个类别进行分析。

现在，既然我们知道时间序列分析的组成部分是什么以及为什么分解时间序列很重要，我们也必须了解“如何”分解它们。

组件的结构或分解

根据时间序列的性质，它可以表示为加法或乘法，其中每个观察都表示为分量的总和或乘积。在季节变化的基础上，让我们学习分解时间序列的两种结构：

• 加法分解——如果季节性变化随时间相对恒定，我们可以使用加法结构分解给定的时间序列。加性结构如下 -

Xt（值）= 趋势 + 随机 + 季节性

• 乘法分解——如果季节性变化随时间增加，我们可以使用乘法结构分解时间序列。乘法结构如下 -

Xt（值）= 趋势 * 随机 * 季节性

这些结构根据季节变化的性质，使数据的各个组成部分被视为一个整体（加法或乘法）。之所以如此，是因为趋势中的数据取决于季节性数据的变动。整个数据是整个系列的更好表示，有助于准确预测。

继续，让我们了解有关时间序列的更多信息，看看它如何帮助预测变量（价格、百分比、金额等）

什么是时间序列预测？

顾名思义，时间序列预测意味着预测那些以时间为成分的变量。在将它用于任何涉及机器学习的任务时，这是一个重要的标准。例如，在使用机器学习预测股票价格时，时间序列分析对于分析不同时间点不同股票价格背后的因素以预测未来价格非常有帮助。

另一个有趣的观察是时间序列预测可用于任何行业来预测变量的未来值。例如，根据当前数据值预测明年 12 月份某些日子的温度。

现在预测涉及从过去时间序列数据的分析中提取的一些数学和统计测试，以预测未来数据。此外，准确预测未来数据集的测试被认为是合适的测试。因此，有一种称为格兰杰因果关系检验的检验来确定过去数据在预测未来值方面的有效性。

格兰杰因果检验

格兰杰因果关系检验可帮助您确定一个时间序列是否可用于预测未来的另一个时间序列。它只是提到如果 X 导致 Y 或 X 是 Y 背后的促成因素，那么基于 X 和 Y 过去值的预测将优于仅基于 Y 过去值的预测。

此外，需要注意的是，这是时间序列数据中最古老的因果关系概念。例如，它基于以下假设：

U - 是宇宙中的所有信息

Y - 需要用宇宙中的所有信息减去来自 X 的信息来预测，所以它将是 U\X。

X- 这个时间序列在过去导致了 Y。

但是由于我们在之前的时间序列中有关于 Y 值的信息，所以我们不包括确定 Y 的 X 的时间序列。

主要概念是丢弃 X 并表明它降低了 Y 的可预测性，因为 X 包含一些关于 Y 的独特且重要的信息。因此，我们说 X-Granger 导致了 Y。

借助方差，我们说：

σ²(Yᵢ|𝒰ᵢ) < σ²(Yᵢ|𝒰ᵢ\𝒳ᵢ)

在上面的等式中，X 和 Y 是平稳随机（随机）过程。

𝒰ᵢ =(U ᵢ₋₁ ,…,U ᵢ₋∞) - 直到时间 i 的宇宙信息。

𝒳ᵢ=(Xᵢ₋₁,…,Xᵢ₋ ∞) - 直到时间 i 的 X 中的信息。

σ²(Yᵢ|𝒰ᵢ) - 在时间 i 使用 Ui 预测 Yi 的方差。

σ²(Yᵢ|𝒰ᵢ\𝒳ᵢ) - 使用 Ui （时间 i ）中除 Xi 之外的所有信息预测 Yi 的方差。

现在，相应地，如果 σ²(Yᵢ|𝒰ᵢ) < σ²(Yᵢ|𝒰ᵢ\𝒳ᵢ) 那么很明显 X Granger 导致 Y 或 X=>Y。

因此，格兰杰因果检验提到时间序列中一个变量的预测取决于其在先前时间序列中的所有贡献因素。

现在让我们转到简单线性预测模型，了解该模型如何帮助预测单个变量或保持时间序列作为组件的任意数量的变量。

简单的线性预测模型

我们将讨论一个简单的线性预测模型，假设时间序列是平稳的并且没有季节性。这里的基本假设是时间序列遵循线性趋势。该模型可以表示为：

预测 (t) = a + b X t

这里的“a”是时间序列在 Y 轴上的截距，“b”是斜率。现在让我们看看 a 和 b 的计算。考虑时间序列“t”的值为 D(t) 的时间序列。

在这个等式中，“n”是样本量。我们可以通过使用上述模型计算 D(t) 的预测值并将这些值与实际观察值进行比较来验证我们的模型。我们可以计算平均误差，它是预测 D(t) 和实际 D(t) 之间差异的平均值。

在我们的股票数据中，D(t) 是 MRF 的调整后收盘价。我们现在将使用 python 计算 a、b、预测值及其误差的值。

请注意，我们正在获取从 2012 年 1 月 1 日到 2017 年 12 月 31 日的“MRF”股票的历史数据

上面的代码给出了如图所示的输出。

线性趋势的斜率（b）为：41.174491162345355

截距（a）为：1269.3446503776584

我们现在可以通过计算预测值和计算 Python 中的平均误差来检查模型的有效性。

输出如图所示：

平均误差为：8.916373244192283e-12

这是否意味着我们的数据没有季节性？请在评论中告诉我。

接下来，让我们看看如何在 Python 中导入、计算和绘制时间序列数据。

如何在 Python 中导入、计算和绘制时间序列数据以进行预测？

我们的主要重点是生成静态预测模型。我们还将通过计算平均误差来检查预测模型的有效性。但是，在继续构建模型之前，我们将简要介绍时间序列的其他一些基本参数，例如移动平均线、趋势、季节性等。

导入数据

我们在本文开头已经导入了必要的库，正如我们在上面看到的，我们将使用 MRF 过去五年的“调整价格”。

我们可以使用我们已经导入的matplotlib库绘制调整后的价格与时间的关系。

stock['Adj Close'].plot(figsize=(10,10),grid =True)

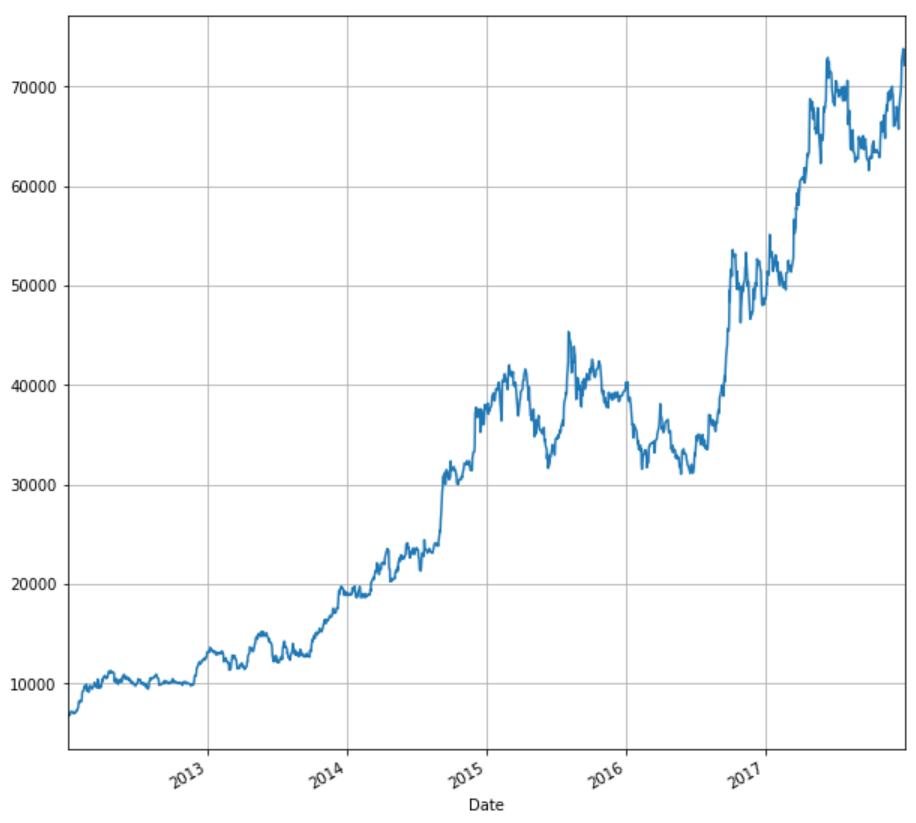
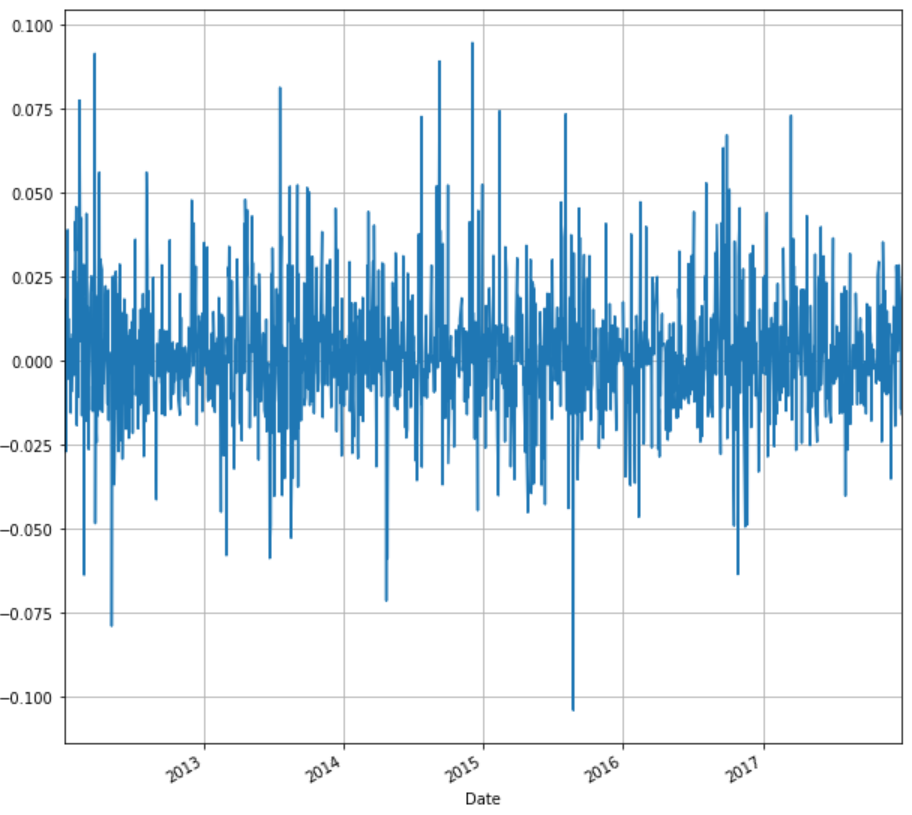
使用时间序列，我们可以计算每日收益并绘制收益与时间的关系图。我们将根据调整后的股票收盘价计算每日收益，并将其存储在列名“ret”下的同一数据框“stock”中。我们还将绘制每日回报与时间的关系。

stock['ret'] = stock['Adj Close'].pct_change()
stock['ret'].plot(figsize=(10,10),grid=True)

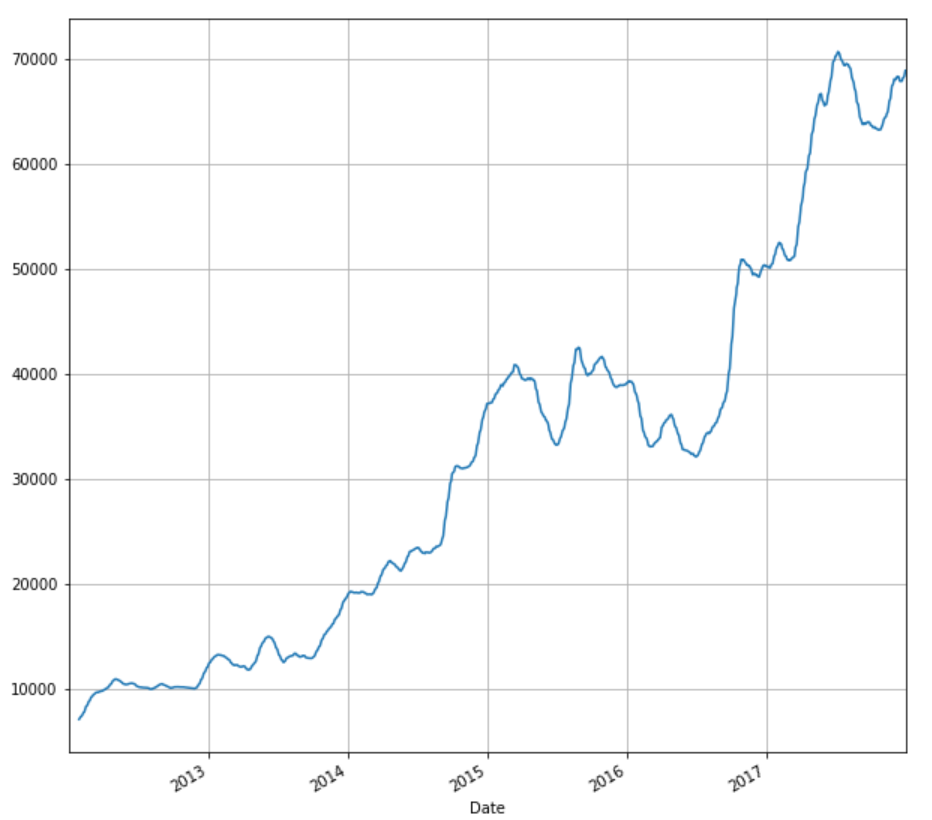
与收益类似，我们可以计算和绘制调整后收盘价的移动平均线。移动平均线是技术分析中广泛使用的一个非常重要的指标。出于说明目的，我们将计算 20 天移动平均线。

stock['20d'] = stock['Adj Close'].rolling(window=20, center=False).mean()
库存['20d'].plot(figsize=(10,10),grid=True)

现在，让我们看看如何在 Python 中使用日期时间数据。

时间序列分析：在 Python 中处理日期时间数据

由于交易者处理大量历史数据，并且需要进行分析和分析，因此日期时间数据很重要。这些工具用于在进行所需分析之前准备数据。我们将主要关注如何处理时间序列的日期和频率。此外，我们将讨论时间序列上的索引、切片和切片操作。对于这个博客，我们将广泛使用“日期时间”库。

让我们从在 python 程序中导入这个库开始：

# 导入需要的模块
从日期时间导入日期时间
从日期时间导入时间增量

因此，这里先讨论基本工具，以使概念更清晰。

首先，让我们将当前日期和时间保存在变量“current_time”中。下面的代码将执行相同的操作。

# 打印当前日期和时间
current_time = datetime.now()
当前时间

datetime.datetime(2020, 2, 22, 1, 18, 57, 478280)

当然，根据您运行代码的时间，输出会发生变化。我们可以使用 datetime 计算两个日期之间的差异。

# 计算两个日期之间的差异（14/02/2018 和 01/01/2018 09:15AM）
delta = datetime(2018,2,14)-datetime(2018,1,1,9,15)
三角洲

输出：datetime.timedelta(43, 53100)

我们可以使用以下方法将输出转换为天或秒：

# 将输出转换为天数
delta.days

输出：43

如果我们想把它转换成秒，我们可以使用下面的代码。

# 将输出转换为秒
增量秒

输出：53100

如果我们想改变日期，我们可以使用我们已经导入的 timedelta 模块。

# 使用 timedelta 移动日期
my_date = datetime(2018,2,10)

# 将日期移动 10 天
my_date + timedelta(10)

输出：datetime.datetime(2018, 2, 20, 0, 0)

我们还可以使用 timedelta 函数的倍数。

# 使用timedelta函数的倍数
my_date - 2*timedelta(10)

输出：datetime.datetime(2018, 1, 21, 0, 0)

我们已经看到 datetime 模块的 'datetime' 和 'timedelta' 数据类型。让我们简要介绍一下在分析时间序列时非常有用的主要数据类型。

我们可以将日期时间格式转换为字符串并将其保存在字符串变量下，让我们看看如何。

字符串和日期时间之间的转换

正如我们提到的日期时间格式的转换，也可以反过来，将表示日期的字符串转换为日期时间数据类型。

输出：

'2018-02-14 00:00:00'

datetime.datetime(2018, 2, 14, 0, 0)

我们也可以使用 pandas 来处理日期。让我们首先导入熊猫。

输出：

DatetimeIndex(['2018-01-14', '2018-02-14'], dtype='datetime64[ns]', freq=None)

在 pandas 中，时间上的缺失时间或 NA 值表示为 NaT（不是时间）。

现在让我们了解时间序列的提前索引和切片。

时间序列的索引和切片

要了解时间序列上的各种操作，让我们使用随机数创建一个时间序列。

输出：

2011-01-02 1.380330

2011-01-05 -0.765646

2011-01-07 0.983679

2011-01-08 0.338122

2011-01-10 -0.919227

2011-01-12 0.577716

这个时间序列的元素可以像任何其他熊猫系列一样使用如图所示的索引来调用。ts['01/02/2011'] 或 ts['20110102'] 将给出相同的输出 1.380330。

切片也类似于我们对其他熊猫系列的切片。

# 对时间序列进行切片
ts[日期时间（2011,1,7）：]

输出：

2011-01-07 0.983679

2011-01-08 0.338122

2011-01-10 -0.919227

2011-01-12 0.577716

现在，让我们看看如果您的时间序列包含重复的索引会发生什么。

时间序列中的重复索引

有时您的时间序列可能包含重复的索引。让我们考虑下面的时间序列。

输出：

2018-01-01 2.081558

2018-01-02 -0.887678

2018-01-02 1.150759

2018-01-02 -1.068980

2018-01-03 0.53671

在上面的时间序列中，我们可以看到“2018-01-02”重复了三次。我们可以使用“index”函数的“is_unique”属性来检查这一点。

dup_ts.index.is_unique

输出：假

我们可以使用“groupby”功能聚合具有相同索引的记录。

分组=dup_ts.groupby(级别=0)

我们现在可以根据我们的要求使用这些记录的均值、计数或总和。

grouped.mean()

输出：

2018-01-01 2.081558

2018-01-02 -0.268633

2018-01-03 0.536711

分组计数（）

输出：

2018-01-01 1

2018-01-02 3

2018-01-03 1

分组.sum()

输出：

2018-01-01 2.081558

2018-01-02 -0.805899

2018-01-03 0.536711

另外，让我们看看如何移动时间序列的索引。

数据转移

在这里，我们将了解如何使用“移位”函数来移动时间序列的索引。

# 移动时间序列
ts.shift(2)

输出：

2011-01-02 南

2011-01-05 南

2011-01-07 -0.079783

2011-01-08 1.286886

2011-01-10 0.961793

2011-01-12 2.532836

在预测时间序列时，还有另一个概念称为时间序列分析中的均值回归。

时间序列分析中的均值回归

时间序列分析包括分析时间序列数据以尝试提取有用的统计数据并识别数据特征的技术。时间序列预测是使用数学模型根据时间序列数据中先前观察到的值来预测未来值。

现在让我们看一下下图，它代表了铝期货在 93 个交易日内的每日收盘价，这是一个时间序列。

现在，均值回归交易意味着什么？

了解时间序列这个非常重要的概念，均值回归是一个重要的内容。好吧，均值回归交易是另一个重要理论，它表明价格、回报或各种经济指标会随着时间的推移趋向于历史平均值或平均值。这一理论导致了许多交易策略，其中涉及购买或出售一种金融工具，其近期表现与历史平均水平有很大差异，没有任何明显的原因。

例如，假设黄金价格平均每天上涨 10 卢比，而在没有任何重大消息或因素的情况下，一天黄金价格上涨 40 卢比，那么根据均值回归原理，我们可以预期未来几天黄金将下跌，因此黄金价格的平均变化保持不变。在这种情况下，平均修正主义者会卖出黄金，推测未来几天价格会下跌。因此，通过购买他之前卖出的相同数量的黄金来获利，现在价格更低。

下面绘制了一个均值回归时间序列，以便于理解。在这里，黑色水平线代表平均值，蓝色曲线是趋向于回归平均值的时间序列。

此外，重要的是要注意，随机变量的集合被定义为随机或随机过程。如果随机过程的均值和方差随时间保持不变，则称该随机过程是平稳的。此外，平稳时间序列本质上会回归均值，即它会趋向于返回其均值，并且围绕均值的波动幅度将大致相等。此外，由于其有限的常数方差，平稳时间序列不会偏离其均值太远。

而相反，非平稳时间序列将具有时变方差或时变均值或两者兼有，并且不会倾向于恢复其均值。

在金融行业，交易者利用平稳时间序列，在证券价格大幅偏离其历史均值时下单，推测价格恢复至均值。

让我们还观察一下，在非平稳中，数据往往是不可预测的，无法建模或预测。通过对数据进行差分或去趋势，可以将非平稳时间序列转换为平稳时间序列。

在这里，可以通过差分（计算 Yt 和 Yt -1 之间的差异）将随机游走（对象的运动或变量的变化不遵循可辨别的模式或趋势）转换为平稳序列。

下面显示的是非平稳时间序列的图，其中蓝色曲线表示具有确定性趋势 (Yt = α + βt + εt)，红色曲线表示其去趋势的平稳时间序列 (Yt - βt = α + εt) .

继续前进，我们现在将看到基于均值回归的交易策略。

基于均值回归的交易策略

与均值回归交易相关的最简单的交易策略之一是找到指定时期内的平均价格，然后确定价格趋于回归均值的平均值附近的高低范围。当跨越这些范围时，将产生交易信号——在上方越过该范围时下达卖单，在下方越过该范围时下达买进指令。交易者采取逆势头寸，即与价格（或趋势）的走势相反，期望价格恢复到平均水平。

这种策略看起来好得令人难以置信，而且它面临着严重的障碍。移动平均线的回溯期可能包含一些不属于数据集特征的异常价格，这将导致移动平均线错误地反映证券的趋势或趋势的逆转。其次，根据交易者的统计分析，证券定价可能很明显，但他不能确定其他交易者是否进行了完全相同的分析。因为其他交易者不认为证券定价过高，他们会继续购买证券，这会推高价格。如果出现这种情况，这种策略将导致损失。

配对交易是另一种依赖均值回归交易原理的策略。确定了两种联合整合的证券，这些证券的价格之间的价差将是平稳的，因此本质上是均值回归。

配对交易的扩展版本称为统计套利，其中许多共同整合的配对被识别并根据每对的点差分成买入和卖出篮子。配对交易或 Stat Arb 模型的第一步是识别一对共同整合的证券。

用于检查一对证券之间的协整的常用测试之一是增广迪基-富勒测试（ADF 测试）。它测试时间序列样本中存在单位根的原假设。

具有单位根的时间序列，即 1 是序列特征方程的根，是非平稳的。增强的 Dickey-Fuller 统计量，也称为 t 统计量，是一个负数。负数越多，对在某个置信水平上存在单位根的原假设的拒绝就越强，这意味着时间序列是平稳的。t 统计量与临界值参数进行比较，如果 t 统计量小于临界值参数，则检验为正，拒绝原假设。

现在让我们看看协整检查 -ADF 测试。

协整检查 - ADF 测试

考虑下面显示的用于检查协整的 Python 代码：

你可以看到下面的输出：

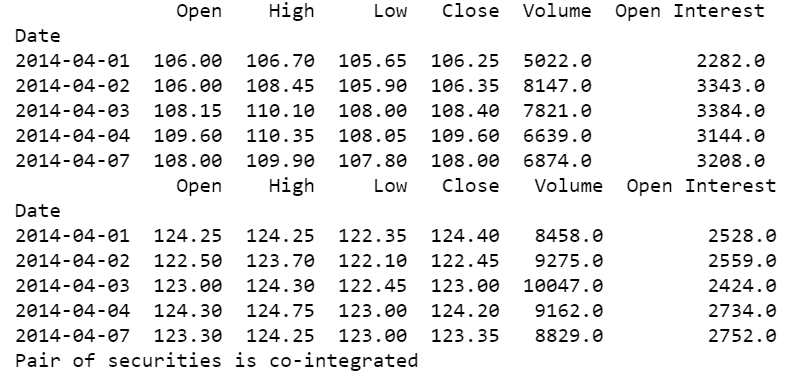
我们首先导入相关库，然后使用 quandl.get() 函数获取两种证券的财务数据。Quandl 通过导入 Quandl 库直接在 Python 中提供金融和经济数据。

在此示例中，我们从 MCX 获取了铝和铅期货的数据。然后我们使用 head() 函数打印提取数据的前五行，以便查看代码正在提取的数据。使用 statsmodels.api 库，我们计算商品对收盘价的普通最小二乘回归，并将回归结果存储在名为“result”的变量中。

接下来，使用 statsmodels.tsa.stattools 库，我们通过将回归的残差作为输入来运行 adfuller 测试，并将该计算的结果存储在数组“ct ”中。

该数组包含 t 统计量、p 值和临界值参数等值。在这里，我们认为显着性水平为 0.1（90% 置信水平）。“c t[0]” 携带 t 统计量，“c t[1]” 包含 p 值，“c t[4]” 存储包含不同置信水平的临界值参数的字典。

对于协整，我们考虑两个条件，首先我们检查 t-stat 是否小于临界值参数 (c t[0] <= c t[4]['10%'])，其次是否 p-值小于显着性水平 (c_t[1] <= 0.1)。如果这两个条件都为真，我们打印“证券对是协整的”，否则打印“证券对不是协整的”。

其他

所以总而言之，时间序列的分析和预测非常重要，它给我们带来了一个很好的结论，即它有助于预测股票价格。

结论

我们首先了解时间序列的含义，为什么在它的基础上进行分析和预测很重要，以及它是如何完成的。归根结底，它是预测变量的一个重要概念。这篇文章帮助了以下核心观点：

• 在分析时间序列时非常有用的基本功能。
• 不同类型的时间序列及其意义，用python计算和绘图
• 一个基于趋势预测时间序列的简单模型，假设时间序列没有季节性。
• 使用日期时间数据和均值回归

\