上周多数风格因子表现良好—因子周报20211205

由crisvalentine创建，最终由crisvalentine更新于2021-12-06 02:39 被浏览 31 用户

摘要

上周多数风格因子表现良好，财务质量、beta因子表现欠佳

上周多数风格因子表现良好，估值、盈利、小市值、反转、波动率、换手率与技术因子均呈现普遍的正收益。成长因子在中证500成分股票池中呈现一定的正收益，但在其余股票池中表现平庸。财务质量因子仅在中证500成分股票池中呈现小幅正收益，在其余股票池回撤；beta因子在全A股股票池呈现微弱的正收益，在其余股票池中回撤。

主动型量化基金近1个月表现弱于非量化基金

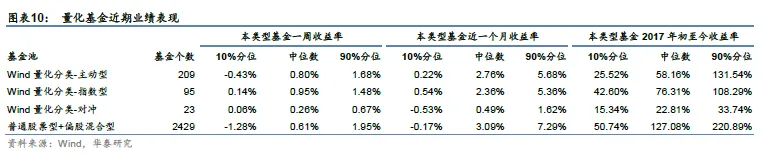
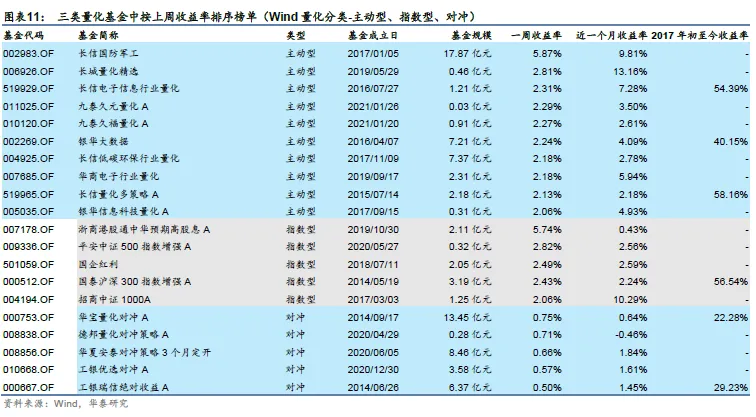
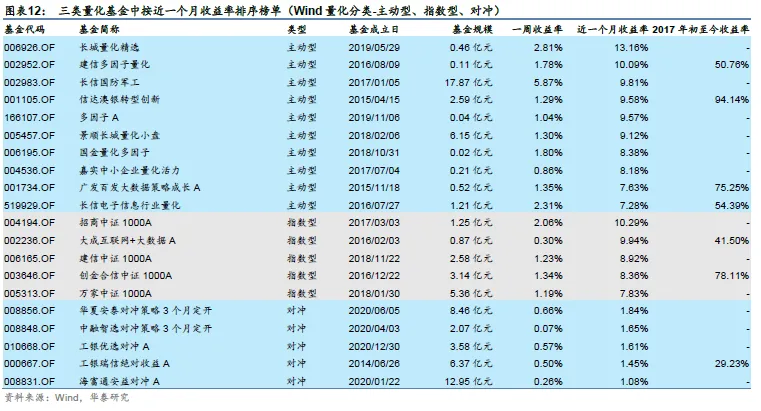
上周主动型、指数型、对冲三个类别的量化基金收益率中位数分别为0.80%、0.95%、0.26%，所有股票及偏股型公募基金收益率中位数为0.61%；近1个月主动型量化基金收益率中位数为2.76%，所有股票及偏股型公募基金收益率中位数为3.09%；主动型量化基金近1周表现强于非量化基金，近1个月表现弱于非量化基金。我们基于结合上期持仓的二次规划法、Lasso回归和逐步回归方法对偏股混合型基金仓位变化情况进行测算，三种方法均显示上周基金仓位预测值较前一周有所下降。

上周市场上行，表现最好的指数是上证综指

上周市场上行，上证综指一周涨幅1.22%相对较大，创业板指一周涨幅0.28%相对较小；观察市场重要规模指数发现，中证500指数一周涨幅1.14%相对较大，沪深300指数一周涨幅0.84%相对较小；上周表现最好的指数是上证综指。在30个中信一级行业中，上周有22个行业处于上涨状态；煤炭、建筑、国防军工行业表现相对较好，涨跌幅分别为8.64%、5.64%、4.54%；消费者服务、医药、传媒行业表现相对较差，涨跌幅分别为-2.61%、-1.83%、-1.40%；电力设备及新能源行业一周成交额领跑其它行业。

风险提示：风格因子的效果与宏观环境和大盘走势密切相关，历史结果不能预测未来；量化与非量化基金的业绩受到多种因素影响，包括环境、政策、基金管理人变化等，过去业绩好的基金不代表未来依然业绩好，投资需谨慎。本报告所采用的基金仓位测算方法仅基于日频基金净值数据和行业数据，没有利用基金报告中公布的重仓股、行业分布等信息，存在一定局限性，敬请注意。

上周市场行情回顾

上周（2021/11/29~2021/12/03）A股市场重要指数和一级行业指数涨跌幅如下所示。

{w:100} {w:100} 上周市场上行。在四个重要的板块指数（上证综指、深证成指、中小板指、创业板指）中，上证综指一周涨幅1.22%相对较大，创业板指一周涨幅0.28%相对较小；在五个重要的规模指数（中证全指、上证50、沪深300、中证500、中证1000）中，中证500指数一周涨幅1.14%相对较大，沪深300指数一周涨幅0.84%相对较小；上周表现最好的指数是上证综指。在30个中信一级行业中，上周有22个行业处于上涨状态；煤炭、建筑、国防军工行业表现相对较好，涨跌幅分别为8.64%、5.64%、4.54%；消费者服务、医药、传媒行业表现相对较差，涨跌幅分别为-2.61%、-1.83%、-1.40%；电力设备及新能源行业一周成交额领跑其它行业。

上周因子表现

我们针对估值、成长、盈利、财务质量、小市值、反转、波动率、换手率、beta、技术共十个风格因子，在沪深300成份股、中证500成份股、中证1000成份股、全A股市场四种股票池内计算行业中性及市值中性的Rank IC值、IC_IR比率，并展示在下面七个图表中。这一计算过程可以简要描述为：

计算附录一表格中所有细分因子的值；
对每个细分因子，用其自身作因变量，用对数总市值和30个一级行业哑变量作自变量进行OLS线性回归，取回归残差替代原始计算的因子值；
对新因子值用中位数法去极值，再标准化，然后将属于同一个风格大类（比如估值）的细分因子直接等权相加作为风格因子的值，与个股下期收益率计算Spearman秩相关系数，即得到该风格因子的Rank IC值；
上周、本月初至今（或指定月份的）Rank IC值分别是用前一周五、上个月（或指定月份前推一个月）的月底作为截面期计算因子值，经过前3步处理后与个股上周、本月初至今（或指定月份的）收益计算相关系数，指定时间区间内Rank IC均值是以自然月为频率计算的月度Rank IC的平均值（本月的Rank IC值即为本月初至今Rank IC值），IC_IR是月度Rank IC的均值除以标准差。

{w:100} {w:100} {w:100} {w:100} {w:100} {w:100} {w:100} 十个风格大类共包含34个细分因子，它们的详细计算方式参见附录一，风格因子合成与IC值计算方法参见附录二，细分因子IC值详表参见附录三。

上周量化基金表现

我们以Wind收集的量化概念类基金（包括主动型、指数型、对冲三个子类）为基础，针对以下几种情形进行调整：

同一只基金可能存在A类、C类或其它类别份额，不同类别份额可以各自对应于独立的基金代码，我们在统计时只考虑成立最久的那一个基金代码（若成立日相同则选A类份额）对应的业绩表现；
去除债券型基金、偏债混合型基金、封闭式基金、非主要投资于A股市场的基金，去除成立三个月之内的基金；
去除明显不是量化型的基金（主要通过基金经理背景、经历和其它信息综合判断）；
我们将所有开放式公募基金中普通股票型和偏股混合型合并作为参照组，因为基金数目众多，细微调整对分位数计算的影响较小，所以对参照组没有进行上述3条处理。

考虑到Wind收集的量化基金可能不全，所以此处讨论的量化基金可以认为是全市场量化基金的一个有代表性的子集。近期量化基金表现如下面图表所示。

首批指数增强型ETF成立

国内首批发行的三只指数增强型ETF于上周公告完成募集，包括两只沪深300指数增强型ETF与一只中证500指数增强型ETF。指数增强型ETF属于主动型ETF，其投资方式类似于一般意义上的主动型基金，以寻求取得超越市场的业绩表现为投资目标；相比场外指数增强型基金，指数增强型ETF交易更灵活，资金使用效率更高，跟踪误差限制更严格；此外，指数增强型ETF每日公布申购赎回清单，申购赎回清单在当日交易所开市前公告。三只指数增强型ETF的募集情况如下：

基金仓位测算观察

正文基于结合上期持仓的二次规划法、Lasso回归和逐步回归三种回归方法，对偏股混合型基金2018年初至今仓位变化情况进行了测算。这一计算过程可以简要描述为：

选取Wind分类下的偏股混合型基金，剔除沪港深基金等非完全投资于A股市场的基金，剔除数据方面有缺失值或存在疑问的基金，剔除2017年以后成立的基金，共保留480只偏股混合型基金。
以过去90个交易日基金的日频收益率作为因变量，30个中信一级行业指数日收益率作为自变量，样本按时间衰减赋权，通过不同的回归方式对各行业变量前的回归系数进行拟合，再求所有回归系数之和，即得基金仓位预测值。
对于结合上期持仓的二次规划法，我们对目标函数进行最优化求解，需要求解的目标向量为仓位向量。目标函数包含两项，第一项是基金日收益率预测值与真实值的均方误差，第二项是基金在各指数的预测仓位与上期真实仓位的误差平方和，λ是第二项损失项前的系数，此处将λ设为10。
对于Lasso回归，其基本原理是在普通最小二乘的损失函数基础上添加L1正则化项，使原本较为病态的回归问题可以正常求解。Lasso回归将某些行业前面的回归系数压缩成0，提取出一组“回归效果最好”的行业组作为解释变量组。Lasso回归具有一个可调参数λ，我们采用10折交叉验证从1e-3至1的范围内搜索最优λ值。
对于逐步回归，我们采用逐步进入方法，每次引入或剔除自变量，都对原模型和新模型进行F检验。如果新自变量的引入能够显著提升模型的解释能力，那么引入该自变量；如果原自变量的剔除不会显著降低模型的解释能力，那么剔除该自变量。直到不再有变量被选入或剔除为止。变量被保留的p值为0.05，被剔除的p值为0.1。

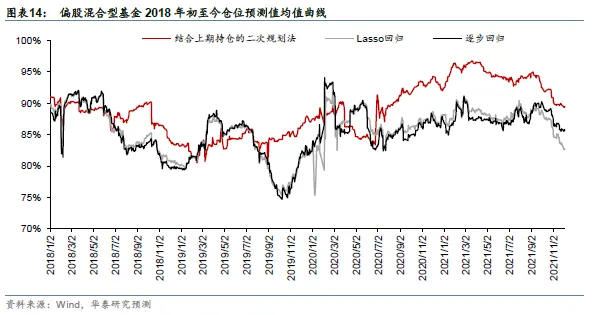
关于回归法进行基金仓位测算的具体方法，感兴趣的投资人可以参阅华泰金工研报《再探回归法测算基金持股仓位》（2018.12.24）了解更多详情。我们使用过去90个交易日的数据进行回归计算，按日滚动回归，得到偏股混合型基金仓位预测值均值变化曲线，如下图所示。结合上期持仓的二次规划法、Lasso回归和逐步回归方法均显示上周偏股混合型基金仓位预测值较前一周下降。

风险提示

风格因子的效果与宏观环境和大盘走势密切相关，历史结果不能预测未来。量化与非量化基金的业绩受到多种因素影响，包括环境、政策、基金管理人变化等，过去业绩好的基金不代表未来依然业绩好，投资需谨慎；基金业绩排名不构成对基金的投资建议。本报告所采用的基金仓位测算方法仅基于日频基金净值数据和行业数据，没有利用基金报告中公布的重仓股、行业分布等信息，存在一定测算误差，敬请注意；基金仓位测算结果不构成对择时的投资建议。

附录一：所有细分因子计算方法

{w:100} 上表第三列因子方向解释：取值为1代表因子值越大越好，-1代表因子值越小越好。当采用等权法合成风格因子时，需将因子值乘以因子方向之后再相加。