Word2Vec介绍:直观理解skip-gram模型
由iquant创建,最终由qxiao 被浏览 10 用户
什么是Skip-gram算法
Skip-gram算法就是在给出目标单词(中心单词)的情况下,预测它的上下文单词(除中心单词外窗口内的其他单词,这里的窗口大小是2,也就是左右各两个单词)。
以下图为例:


图中的love是目标单词,其他是上下文单词,那么我们就是求 、
、
、
。
目标是什么
理解了Skip-gram算法的定义,我们很容易得出:我们的目标是计算在给定单词的条件下,其他单词出现的概率!
问题来了,在实践中,怎么计算这个概率?
接下来让我们一步一步理解这个过程,首先从定义表示法开始。
定义表示法
one-hot向量
one-hot向量就是利用一个 向量来表示单词。
|V|是词汇表中单词的数量。
一个单词在英文词汇表中的索引位置是多少,那么相对应的那一行元素就是1,其他元素都是0。
还是以我们的例句"Do you love deep learning"为例。
love的one-hot向量就是:
由于我们只有5个单词,因此,ong-hot向量的行数是5,love是第3个单词,因此索引3位置的数是1。
我们用 来表示目标单词的one-hot向量。
词向量(word vector)
词向量就是用一组d维的向量代表单词,如下:
注意这是个d维的向量。
这里我们用 表示目标单词的词向量
单词矩阵(word matrix)
单词矩阵是所有单词的词向量的集合。
注意,我们这里要用到两个单词矩阵,一个是目标单词的词向量组成的矩阵,用 表示。
W的尺寸是 。
另外一个矩阵是由除目标单词外的其他单词的词向量的转置组成的矩阵,用 表示,尺寸是
,注意这里与上一个W的尺寸相反,至于为什么我们后面解释。
另外需要说明的是,由于每一个单词都有可能作为目标单词或其他单词,因此,实际上这两个矩阵是分别包含所有单词的词向量的。
单词相似度
我们先考虑这个问题:怎么表示两个单词之间的相似度?
一个简单方法就是:两个单词间的词向量求内积!
这里,我们用 代表目标单词的词向量,
代表除目标单词外窗口内第x个单词的词向量。
那么求内积: 就是两个单词的相似度。
因为两个单词的内积越大,说明两个单词的相似程度越高。
softmax函数
我们需要知道的是softmax函数就是能够把输入转换为概率分布,也就是说使输入的实数变成分数。除此之外的内容我们暂不讨论。
softmax函数的公式如下:


这里面的z就是我们的相似度
最后总结一下,为下一章节做准备:
表示目标单词的one-hot向量。
表示目标单词的词向量
表示除目标单词外第x个单词的词向量
表示目标单词矩阵
表示其他单词矩阵
词向量的维度是d
词汇表的维度是V
理解算法过程
求相似度 总共分几步?
第一步:求
,这里W是
的矩阵,
是
的矩阵,因此
是
的向量。
直观理解:矩阵与one-hot向量的内积,相当于把one-hot向量中索引为1在向量矩阵中对应的那一列提取出来。
第二步:求 组成的向量
这个向量就是 ,这里的
是
的矩阵,
是
的向量。因此
是
的向量。
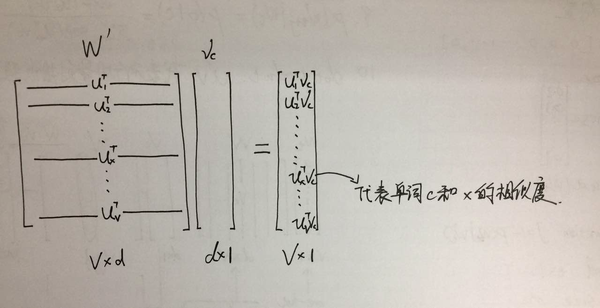
直观理解:下面要说的很重要!用 与
相乘,相当于
和词汇表中的所有词向量的转置都分别求内积,得到的结果组成了一个向量!
下图是直观描述。

第三步:求softmax
这步比较简单,把得到的相似度矩阵代入softmax公式,就得到了一个满足概率分布的矩阵。
至此,我们的目标已经实现:得到了一个向量。
向量中的数值代表在给定单词的条件下,其他单词出现的概率!大功告成!

