如何理解动量与反转?
由crisvalentine创建,最终由crisvalentine 被浏览 127 用户
报 告 摘 要
股票的近期回报可以预测未来风格因子的贝塔
我们发现动量和长期反转能够可以捕捉未来风险因子的贝塔,动量是未来一年市场资产定价因素(例如 Fama-French 五因子模型)的强大预测指标。中长期历史回报与未来贝塔值之间的联系表明,与动量和长期反转相关的溢价可能与条件风险敞口有关,动量捕捉到了随时间变化的风险补偿。
IPCA条件因子定价模型能够捕捉动量溢价
动量特征(过去12个月的回报)包含了股票潜在定价因子风险的时变暴露,因此直接对过去12个月的回报进行排序对未来回报并没有显著预测能力。因此控制这种随时间变化的风险敞口后才能够捕捉到动量溢价。作者提出基于IPCA捕捉潜在定价因子,并以时变的因子载荷对股票进行定价。作者对比了传统动量、IPCA潜在因子带时变载荷后动量、以及残差动量的效果,发现传统动量原始信号并没有收益预测能力,转为截面排序后有一定收益预测效果,而IPCA模型下预测模型非常显著,多空年化回报能够达到33.6%,而残差动量几乎没有预测能力。并且,在控制了IPCA模型的条件预期收益后,传统动量不再有预测能力。
文献来源
文献来源:Kelly, Bryan T., Tobias J. Moskowitz, and Seth Pruitt. "Understanding momentum and reversal." Journal of Financial Economics 140.3 (2021): 726-743.
文献亮点:作者提出了条件因子定价模型,其基于IPCA构建潜在定价因子,并动态估计其时变因子载荷,基于该模型可以显著解释相当大一部分动量和长期反转的回报,并可用于产生非常显著回报的收益预测。
引言
自 Jegadeesh 和 Titman (1993) 提出动量异象以来,动量异象一直是金融经济学中最受广泛研究的主题之一。它构成了整个资产管理行业使用策略的基础,也是大量共同基金和交易产品的基础。尽管它对金融业产生了广泛的影响,但动量仍然是一种较为神秘的异象。虽然从行为和理性上都已经提出了各种理论来解释动量,但没有一个被广泛接受。经验资产定价模型如 Fama 和 French (2015) 五因子模型无法解释动量异象,目前的研究也尚未找到风险暴露能够解释与近期股价相关的横截面回报溢价。因此,动量通常是市场是否有效的辩论核心。
本文的目的是通过条件经验资产定价模型的视角重新评估动量异象。有多少动量溢价可以用条件风险敞口来解释?我们的核心发现是,股票的条件风险溢价的变化通过不同的因子敞口从而与动量密切相关,这些因子敞口在动量风险溢价的变化中占主导地位。在我们的数据中,经典的动量策略(按过去t-2至t-12个月原始收益排序股票的前五分之一对冲后五分之一)产生了8.3%的显著年化收益。然而,当从我们的条件模型中剔除其他定价因素的敞口时,残差动量策略(对与条件因子无关的收益的残差成分进行排序)每年产生4.4%的边际显著收益。相反,根据来自条件模型的收益的预测成分对股票进行排序会产生三到四倍的动量收益。由此可见,我们条件模型中的因子很好地解释了大部分无条件动量效应。相对于静态Fama和French(2015)五因子模型,动量策略的年化alpha为9.2% (t-stat=3.0),而相对于我们的动态因子,它的alpha为负且不显著(alpha为-3.2%, t-stat=-1.2)。
通过仔细构建更准确地代表条件风险回报的因子,并适当指定这些因子的时变条件贝塔系数,我们发现动量异象收益对常见的风险敞口有大量暴露。虽然我们不是第一个尝试用条件风险模型作为对动量(Conrad和Kaul(1998);Jegadeesh和Titman(2002);Grundy和Martin(2001);Chordia和 Shivakumar(2002) )或长期反转(Kothari和Shanken(1992)),我们提取条件风险溢价的方法在解释这些过去的回报现象方面更加成功。我们探索并解释了我们的方法如何以及为什么会取得如此成功。
我们首先建立了动量可解释的必要条件,即动量可以捕捉因子风险敞口的因子定价模型。我们可以看到动量是未来一年市场回报本身以及其他流行资产定价因素(例如 Fama 和 French(2015)五因子模型)的强大预测指标。动量特征对未来贝塔的预测能力在统计上和经济上都很强。例如,市场贝塔系数的估计预测系数表明,当一只股票从动量特征的第10个百分点移动到第90个百分点时,其市场贝塔系数增加0.20。这是动量捕捉条件风险敞口的初步迹象。同样,长期反转,另一个历史回报特征,对贝塔系数有类似的预测能力,但短期反转对贝塔系数的预测能力要弱得多。中长期历史回报与未来贝塔值之间的联系表明,与动量和长期反转相关的溢价可能至少部分与条件风险敞口有关。然而,仅凭条件市场贝塔系数的增加幅度不足以解释高动量和低动量(或长期反转)股票之间的回报差异。因此,资本资产定价模型 (CAPM) 的有条件版本无法解释这些回报。
为了严格研究贝塔可预测性是否在数量上合理化了与价格趋势相关的平均回报模式,我们需要一个不仅仅包含市场因子的资产定价模型。为了研究这个想法,我们分析了一个通用的条件因子定价模型,形式为
虽然条件因子模型为动量和其他价格趋势模式提供了潜在的概念解释,但它们难以估计。一种估计方法是使用可观察因子并估计滚动贝塔系数。然而,可观察因子可能会被错误指定——特别是如果在它们最初被构建为用作无条件因子(例如,Fama-French 因子)时被重新解释为条件因子,并且滚动贝塔可能会遭受“陈旧偏差”,因为它们只是缓慢地纳入条件信息。另一种选择是根据较高频率(例如,每日)数据估算每月已实现的贝塔系数。但仅用每月 20 次的日度样本,已实现贝塔往往是嘈杂的,并且扩展到几个月会重新引入潜在的陈旧性。另外,这些都不能解决可观察因子中的错误指定问题。
我们的研究问题与有关动量和长期反转的文献中的四个前期研究最密切相关。首先,Conrad 和 Kaul(1998)认为股票预期收益的差异可以解释动量收益。Jegadeesh 和 Titman (2002) 反对这种解释,因为它基于无条件预期并没有足够的分散度来解释动量回报。此外,如上所述,基于无条件预期的解释不会导致动量策略所涉及的股票多空排序的变化,也无法解释长期反转的结果。另一方面,基于条件期望的解释可以并且确实解释了这些模式。
其次,Grundy 和 Martin (2001) 将收益分解为系统风险成分(捕获为暴露于 Fama 和 French三因子,1993)和特定于股票的残差,并且发现动量现象完全由残差收益的动量驱动。我们发现 Grundy 和 Martin (2001) 的结论很可能是由因子模型错误指定导致的,由于可观察因子的滚动窗口贝塔估计。使用具有缓慢移动的贝塔和错误因子的模型几乎可以确保残差继承了预期收益的重要变化,从而给人一种误导性的印象,即动量是异质收益的一个特征。相比之下,一旦我们考虑到潜在因素和条件贝塔动态,我们就会发现残差动量的微弱证据。我们论证并表明,正是这种经过改进的模型导致了与 Grundy 和 Martin (2001) 不同的结论。
第三,Chordia 和 Shivakumar (2002) 将股票收益分解为一个可通过宏观经济预测变量和不可预测的冲击进行预测的组成部分。他们得出结论,动量回报最好通过宏观经济变量预测的条件预期回报而不是残差来获得。他们推测可预测成分代表动态因素风险溢价(与 Grundy 和 Martin (2001)的结论相反)。然而,他们没有验证这个猜想。此外,预先设定的宏观因素也为错误指定提供了空间,可能无法捕捉有条件的风险敞口。我们的报告提供了动量回报和因子风险敞口之间的明确缺失联系。
历史回报预测贝塔
在本节中,我们展示了一个稳健的事实,即股票最近的历史回报可以预测其未来在总体风险因素上的贝塔系数。
数据
我们的数据集是在KPS中研究的数据集,由Freyberger(2020)中的股票收益和36个特征组成。该样本从1966年至2014年,将注意力限制在所有 36 个特征均未缺失的股票月度观察值上,最终包括12813只股票和1403544个股票月份观察值。为了处理异常值,对每个特征进行横截面排序,然后将这些排序除以该横截面中的股票数量,然后对它们进行横截面去均值,使其保持在[-0.5,0.5]区间内。
市场贝塔预测结果
我们首先检查与产生正异常回报的各种交易策略相关的特征,尤其是与历史回报相关的特征,是否对未来市场贝塔系数的变化具有可预测性。大量文献表明,这些特征产生了静态 CAPM 无法捕捉到的异常回报可预测性,这意味着与这些特征相关的无条件市场贝塔系数的变化不足以解释它们的回报。在许多情况下,基于这些特征的多头/空头投资组合的无条件市场贝塔系数接近于零。但是,如果风险敞口发生变化,这些特征可能与未来的贝塔系数相关,因此条件风险模型可能会更好地捕捉其回报。作为一个简单的起点,我们检查这些特征是否可以预测未来的市场贝塔系数,然后继续检查具有时变风险敞口的多因子模型。
我们使用在第 t 月内的每日回报数据构建股票级别的月度OLS市场回报的贝塔系数。我们还根据 t 至 t + 2 个月的每日数据构建季度贝塔系数,根据 t 至 t + 5 个月的每日数据构建半年度贝塔系数,以及根据 t 至 t + 11 个月的每日数据构建年度贝塔系数。然后,我们使用最近的股票动量探索已实现贝塔系数的可预测性。我们在股票月面板中对从 t-12 月到 t-2 月(Asness(1994),Fama French(1996) 的标准动量)的累积回报以及其他特征(按股票和按月对标准误差进行聚类)对 t 月到 t + h (h=0,2,5,11) 月的 beta 进行回归。
下图中的结果表明,股票动量是未来实现的市场贝塔系数的有力预测指标。1 个月已实现市场贝塔系数的预测系数为0.23 (t=11.88)。该系数意味着,当股票从第10动量百分位过渡到第90动量百分位时,其市场贝塔系数增加0.18 (0.23x0.8),或等效地,其市场风险溢价增加18%。根据3、6和12个月的未来每日回报计算的已实现贝塔系数的结果相似。
虽然市场贝塔可预测性很强,但动量股顶部和底部十分之一之间0.18 贝塔差异的经济幅度不足以解释其平均回报的差异。即使市场风险溢价为6%,0.18的 beta 差异也只能解释8%-9%动量溢价1.1个百分点左右。因此,只有随时间变化的市场贝塔系数的条件 CAPM 无法捕捉动量收益。出于这个原因,我们在下面探索了一个更丰富的条件多因子模型。
动量在预测未来实现的贝塔值方面并不是独一无二的。长期反转,另一个历史回报特征,基于之前三到五年的回报,也显著预测了未来的市场贝塔系数,尽管预测系数是动量的一半,如下图所示。许多其他常见的特征也显著预测了已实现的贝塔系数。自然,最强的贝塔预测器之一是过去实现的贝塔(市场贝塔),以及规模(市值)。然而,正如该图在多因子回归中显示的那样,即使考虑了这些特征,动量和长期反转特征对于预测市场贝塔值仍然非常重要。
最后,短期反转,另一个基于过去一个月回报的历史回报特征,是对未来市场贝塔系数具有统计显著性但在经济上很小的预测性特征。这种微弱的结果与短期反转与流动性影响(例如 Nagel(2012))的联系比时变风险更大是一致的。
多因子贝塔预测结果
由于我们将在下面考虑多因子模型,因此评估历史回报如何相对于通常用于代表总风险的其他因子预测贝塔值是有用的。下图报告了运行回归方程的结果。公式(2) 使用 Fama 和 French (2015) 中的因子 Small Minus Big (SMB)、High Minus Low (HML)、Robust Minus Weak (RMW) 和 Conservative Minus Aggressive (CMA) 的年度 Beta 值代替市场 Beta,其中贝塔值是以相同的方式使用每日回报计算的。除了 SMB 之外,动量显著预测 HML、RMW 和 CMA 中的每一个的 beta 敞口,即使在控制账面市值比、毛利润率和投资时也是如此,它们分别是HML、RMW 和 CMA 所基于的特征。长期反转还显示出对所有四个因子的未来贝塔系数的显著可预测性。最后,短期反转对未来贝塔系数的可预测性很小且微不足道,这与其对市场贝塔系数的缺乏可预测性及其主要是流动性驱动的现象一致。这些贝塔预测结果的结论是,许多“异常”特征,特别是那些基于历史回报(例如动量和长期反转)的特征,是未来已实现风险的有力指标,即使仅通过简单的视角来看待风险、一维 CAPM 或通过多因子模型,例如 Fama 和 French (2015) 五因子模型。因子贝塔值随时间变化显著,股票特征对于跟踪贝塔值变化似乎很有用。这一发现暗示了在风险和回报的动态条件模型中调和与股票特征相关的平均回报模式的途径,即那些基于历史回报的模式。我们接下来通过查看动态多因子模型来探索这条路线。
模型
我们为个股假设了一个条件因子定价模型,并研究该模型解释预期回报的动量和长期反转效应的可行性。条件通过因子载荷进入我们的模型,我们将其指定为股票特征的函数。随着股票的特征发生变化,其条件风险敞口也会发生变化,因此其模型隐含的预期收益也会发生变化。从模型的角度来看,股票表现的任何相对持久性——例如由动量策略捕获的——必须源自风险敞口的相对持久性。
主要的实证挑战是建立一个条件资产定价模型。我们使用股票特征作为工具来帮助识别股票难以衡量的动态因子敞口,我们探索了两种模型变体。第一种使用 IPCA,它将因子视为潜在因子,并估计与基于特征的风险敞口最相关的因子。第二个和更具限制性的模型依赖于可观察的预指定因子,例如 Fama-French因子。
IPCA
特征和载荷之间的 IPCA 映射提供了特征和因子 beta 之间的统计桥梁。公式 (1) 中所示模型的“受限”形式也强加了特征影响预期收益是因为它们决定了 beta。这种形式的模型将因子模型截距 (alpha) 设为零,强加了经济限制,即风险溢价仅反映对协方差风险敞口的补偿。在此限制下,如果模型代表因子风险,则该模型只能适应动量效应,定义为与此估计程序恢复的潜在因子的协方差。共同风险是否产生动量(和长期反转)是一个经验问题。如果由资产特定回报产生的异常 alpha能够更好地解释动量或其他过去的回报效应,则上述受限模型将不会产生动量,并且会被其他模型超越。我们在下文中研究这些测试结果。
工具化Fama-French模型
KPS 研究的最佳条件模型使用潜在因子模型。然而,他们还发现具有可观察因子的标准模型,例如Fama-French 五因子模型,当其载荷具有可观察特征时得到了显着改善。在 Fama-French 载荷规范中包含特征,将可观察因子模型置于与 IPCA 相同的信息基础上。
动量模型
条件模型是否能解释动量和反转
我们评估了 IPCA 在大量规范和数据集中解释动量的能力,包括样本内和样本外。 我们还研究了在使用 2-12 以外的一系列替代形式窗口时我们的发现有何不同,并发现我们基于模型的条件预期解释了大部分动量和长期反转现象。我们还发现短期反转是 IPCA 没有捕捉到的一种独特现象。
IPCA模型
下图展示了IPCA模型解释动量效应的实验结果。其中PanelA采用如下的面板回归模型来预测:
最后,我们考虑 IPCA 预测残差的动量。在单变量分析中,残差动量的预测能力弱于总回报动量的预测能力。排序信号的单变量斜率系数降至微不足道的 0.30 (t-stat=1.3),而Q5-Q1夏普比率降至微不足道的0.30(t-stat=1.9)。转到面板 B,我们发现我们的基于因子模型的策略比原始动量更有利可图,而残差动量策略产生的利润微乎其微。
单变量测试表明,该模型比简单的动量信号产生更有效的回报预测。对条件模型解释动量的能力的更直接测试是同时进行控制动量和基于模型的预期回报的联合预测回归。这些二元回归显示在面板 C 中。我们发现动量的预测效果主要包含在基于模型的预期回报中。控制条件模型,动量信号失去显著性,甚至切换方向。无论我们是比较原始动量信号还是横截面排序动量信号(第 1 和第 4 列),这一事实都成立。基于模型的预期回报似乎包含了动量信号提供的所有预测信息。这些结果表明,源自动态因子敞口的条件预期收益是动量体现的可预测性的主要原因。
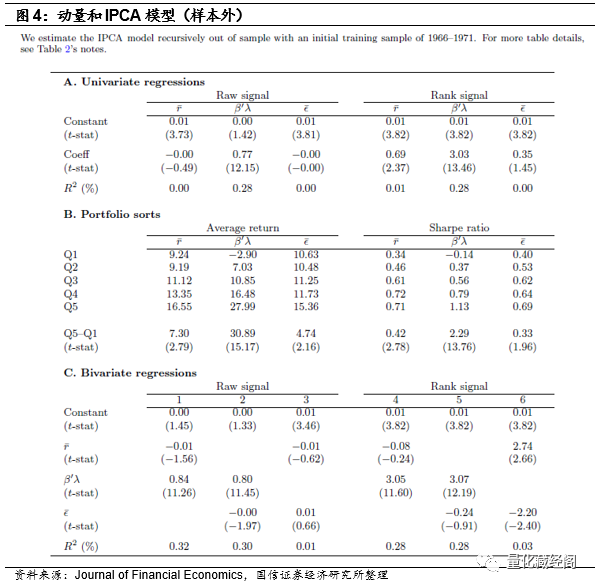
IPCA样本外
图 B 显示基于模型的预测的交易策略性能不是样本内过度拟合的产物。虽然样本外 Q5-Q1 年化平均回报率 30.9% 和夏普比率 2.29(分别与样本内 33.6% 和 2.39 相比)略有衰减,但它仍然是简单动量的四倍多。残差动量策略的年化夏普比率为0.33(t-stat=1.96),带来了略微显著的盈利能力。

 解释
解释
我们需要了解我们所说的 IPCA 模型“解释”动量的含义。我们的结果意味着动量特征(过去 12 个月的回报)反映了潜在因子风险的时变暴露,通过回报的协方差矩阵定义。对过去 12 个月的回报进行排序是对经济中定价因子的条件 Beta 敞口进行排序的一种嘈杂的衡量方法。因此,控制这种随时间变化的风险敞口的准确度量可以捕获大部分动量溢价。过去的回报是捕捉定价因素的协方差风险的一种简单的临时方法。从经济上讲,这些结果意味着过去的回报异象会受到定价因子的条件协方差的影响,但我们还不知道为什么这些因子被定价。换句话说,我们的模型使用已知与来自大量经验文献的平均回报相关的特征来构建潜在因子暴露,其动态恰好被简单的回报移动平均线合理地吸收。但是我们的框架(和文献)对于为什么这些特征与市场平均回报相关,或者它们代表什么经济风险或状态变量保持沉默。这个问题仍然难以捉摸,超出了本文的范围。
结论
股票动量、长期反转和其他预测未来回报的历史回报特征同样可以用来预测未来的贝塔值,表明这些特征捕捉到了随时间变化的风险补偿。我们用条件因子定价模型将这一论点形式化。我们基于IPCA并依靠可观察到的股票特征来估计潜在因子及其时变因子载荷。我们发现即使在短期范围内(一年),因子载荷也会发生显著变化,并且这种变化捕获了现有文献中常用因子模型所捕捉不到的显著条件风险溢价。我们对条件风险敞口的估计可以解释相当大一部分动量和长期反转的回报,并可用于产生非常显著的回报预测。