研究背景与动机 [page::0][page::1][page::2]

• 高阶矩（如coskewness）在金融投资组合优化中备受关注，但在精算领域尚未充分研究。

- 报告旨在探讨高阶混合矩在保险资本要求、风险资本分配及人寿年金估值中的作用。

• 选取指数分布作为边际分布并采用混合copula建模依赖结构。

量化高阶混合矩上下界的方法推导 [page::3][page::4][page::5][page::6][page::7]

• 通过扩展Bernard et al. (2023)方法，严格推导了$\mathbb{E}(X1 X2^{d})$的最小值和最大值以及对应的依赖结构（copula）。

- 关键数学工具包括反分布函数、导数以及指示函数，覆盖一般边际分布和所有正整数$d$。

• 特殊边际分布如均匀分布、指数分布等给出了明确的解析表达和对应copula支持区形态图示。

标准化秩系数（Standardized Rank Coefficients）及性质 [page::13][page::14]

• 定义了一系列标准化秩系数 $RSd$，取值区间固定为[-1,1]，且依赖于边际分布的秩函数，具备严格单调变换不变性。

- 该指标相比已有非标准化秩coskewness更便于解释和跨数据集比较。

量化高阶矩对保险关键指标的影响分析

资本要求（ES） [page::16][page::17][page::18]

• 采用混合copula模型模拟两条保险业务线损失，分析$\mu{2k}$对条件风险度量ES的影响。

- 结果表明ES随着高阶混合矩（coskewness）增大而单调递增，且保障水平越高，差异越明显。

风险资本分配（MES） [page::19][page::20]

• MES用于衡量单个风险对系统性风险的边际贡献，在同一模型下进行数值模拟。

- MES与高阶混合矩的关系复杂：大部分情况下MES随混合矩增加而增，但某些参数配置下MES几乎不变，需谨慎解读coskewness对系统风险贡献的影响。

多人生存年金估值 [page::21][page::22][page::23]

• 考虑夫妻双方未来寿命的依赖结构，研究高阶混合矩对联合生存及最后生存年金价值的影响。

- 发现依赖强度越大，最后生存年金价值上升，而联合生存年金价值下降，且区别随期限延长而拉大。

实践意义总结 [page::23]

• 降低资产层面的coskewness可有助于资本要求的减小，但不一定降低系统风险贡献（MES），投资组合和监管策略需系统考量。

- 对于寿险产品，误判依赖结构特别是高阶混合矩可能导致重大定价偏误，需审慎建模。

高阶矩在依赖不确定性下的界限及其在保险中的应用 — 深度分析报告

---

1. 元数据与报告概览

• 报告标题：Higher moments under dependence uncertainty with applications in insurance

- 作者：Carole Bernard, Jinghui Chen, Steven Vanduffel

• 发布日期：2025年8月26日

- 主题领域：高阶矩及其在金融风险度量与精算科学中的应用，特别是依赖结构不确定性背景下的风险界限、保险风险资本配置及年金估值。

• 核心论点：报告聚焦于高阶混合矩（如协偏度）的边界问题，在仅知边际分布但依赖结构未知时，推导 $\mathbb{E}(X1 X2^d)$ 的最小值和最大值。并运用这些结果分析精算领域关键风险指标（如期望损失ES、边际期望损失MES）和人寿年金定价的影响。同时，提出标准化秩系数（standardized rank coefficients）作为一种新的不依赖于边际分布的依赖度量。研究结果既丰富了理论体系，也对保险监管和风险管理有实用指导意义。[page::0]

---

2. 逐节深度解读

2.1 引言（第1-3页）

• 内容与重点：

- 高阶矩（二阶方差以外）在金融投资组合优化与资产定价中的重要性，特别是协偏度与协峰度。
- 现代金融理论对风险衡量的扩展，从传统的均值-方差模型（Markowitz）到考虑高阶矩的资产价格模型（Harvey and Siddique等）。
- 目前精算科学多聚焦于二阶矩，对高阶中心混合矩的研究仍较少。
- ES和MES成为保险风险资本配置和资产管理的主流度量工具，报告拟将高阶混合矩的分析引入这些领域，并兼顾人寿年金中的寿命依赖性问题。
- 利用copula理论与边际分布已知而依赖未知的框架，力图解决混合矩的极值边界，并提出适用的依赖结构。
- 说明采用某些常用分布模型（如指数分布）以兼顾解析解和实际精算需求。

• 逻辑和假设：

- 组合回报的期望效用可通过高阶泰勒展开表示，展开式中的高阶中心混合矩（如协偏度）有显著意义。
- 影响资产收益及损失建模的风险度量扩展至高阶矩是合理且必要的，尤其是在极端市场条件和寿命相关风险环境。
- 依赖结构未知是实际中普遍存在的挑战，需针对这一不确定进行风险边界估计。

• 引用：

- 多篇经典文献支持金融领域高阶矩的重要性（Samuelson, 1970; Harvey et al., 2010等）。
- 精算领域风险资本与定价的文献多数聚焦于二阶矩（Furman and Zitikis、Godin等）。
- 监管趋势转向使用ES替代VaR（Solvency III, Basel III）。

2.2 第2章：混合矩的上下界及解析表达（第4-11页）

• 关键论断：

- 在已知 $X1 \sim F1, X2 \sim F2$ ，但依赖未知条件下，推导混合矩 $\mathbb{E}(X1 X2^d)$ 的上下界（$\inf$和$\sup$）。
- 运用概率量化函数和分布逆（quantile function），构造达到上下界的极端依赖结构（copulas）。
- Theorem 2.1给出上下界的具体表达及对应copula的构造方法，区分了$X2$是否跨零范围及次数$d$为奇偶的情况。
- 提出两种推广：边际对称（零均值对称分布）以及均匀分布的显式边界及copula。
- 推导中合理利用交换变量等技术，巧妙分割抽样空间，给出概率分配（权重变量$J$）以及相应分片函数$g^{-1}$和$f^{-1}$，以实现精准的反函数表达。

• 重要数据点和例子：

- Proposition 2.3针对均匀分布边界完整公式，明确了上下界数值与copula结构。
- Proposition 2.4则讨论了指数分布情况，符合保险寿命模型需求。
- 图1和图2以及图3分别通过图形直观展示上下界的copula支持以及所用函数的形状和分布关系。

• 模型假设与方法：

- 边际分布已知且存在解析反函数。
- 标准均匀随机变量$U,V$独立，用于构造实现极值的依赖结构随机变量$U1,U2$。
- 上下界构造采用Lemma 2.1和2.2的最大和最小积算子原理。

• 复杂概念解释：

- $F^{-1}$：分布函数的广义反函数，即分位数函数，常用于边际转化。
- $g^{-1}, f^{-1}$：由$g(x) = x - F2(-F2^{-1}(x))$构造的辅助函数，用于描述分布对称变换的关系。
- copula：定义随机变量联合分布的依赖结构函数，核心工具用于边际固定时刻画变量依赖。
- 指标函数$J$和$ I$用于在复合依赖结构中随机选择不同分支。

2.3 第3章：高阶矩在依赖不确定性下的风险界限与秩相关系数（第12-15页）

• 混合矩中心化及标准化：

- 定义高阶中心混合矩 $\mud(X1,X2) = \mathbb{E} \left[ \frac{X1-\mu1}{\sigma1} \left(\frac{X2-\mu2}{\sigma2}\right)^d \right]$。
- 该定义使混合矩不依赖于均值和方差，更关注变量间的依赖结构。

• 界限计算：

- 利用前章结果对标准化混合矩 $\mud$ 求最大最小界限（Proposition 3.1），给出具体copula实现方式。
- 重要结论包括对具体分布（正态、指数、学生t分布等）风险界限的计算示例，列示风险界限存在的对称性与非对称性。
- 表1系统展现多种分布下协偏度的极值界限，体现理论的广泛应用潜力。

• 标准化秩系数提出：

- 引入新的依赖度量，即标准化秩系数 $RSd$，基于变量的分布函数转化，将依赖度量规约至[-1,1]区间。
- 与传统秩相关（如Spearman）类似，但更强调高阶矩相关。
- $RSd$满足不变量性、边界取达性等性质，且更便于理解和比较。

2.4 第4章：高阶混合矩对保险核心问题的影响（第15-23页）

• 模型设定与工具：

- 双指数边际模型 $Xi \sim \mathrm{Expon}(\lambdai)$，依赖以混合copula $C\lambda$模拟：参数 $\lambda \in [0,1]$调节依赖强度，因而调节混合矩高低。
- $\mud(X1,X2)$呈线性函数于$\lambda$，实现从极小到极大。

• 4.2 保险资本要求（ES）：

- 利用ES评估合并风险$S=L1 + L2$。
- 通过仿真计算不同混合矩极值（$\lambda=0$和$\lambda=1$）下ES，发现高混合矩对应更高ES。
- ES与混合矩的积累效应随风险对应的概率$ p $增大而更显著。
- 表3细化说明不同参数$\lambda1$, $\lambda2$及置信水平$p$对ES影响的差异性。
- 实务角度提示可通过降低目标业务线与现业务的高阶混合矩，优化资本占用。

• 4.3 风险资本分配（MES）：

- 通过MES衡量单一风险对整体系统风险的边际贡献。
- MES在混合矩变化下的反应较ES更复杂，部分参数下随依赖变化单调增加，部分情况下MES近似不变。
- 这一非单调现象强调MES对依赖结构的敏感度复杂，风险管理需谨慎解读混合矩变化带来的系统风险变化。
- 表4和图5提供了详细数值模拟结果支持此观察。
- 结论强调降协偏度并不必然降低系统风险贡献。

• 4.4 人寿年金定价：

- 模拟夫妻未来寿命$Tx,Ty$为指数分布，利用混合copula刻画寿命依赖。
- 考虑联生年金与末存年金两类产品，分别对应最小和最大生存时间的收益权利。
- 计算得到，混合矩提高时：末存年金价值上涨，联生年金价值下降，且二者价格差距随年期增长扩大。
- 通过加拿大人口统计数据实证标定参数，模拟结果与实际稳定性可行。
- 表5展示不同年期$n$与依赖参数$\lambda$组合下年金价值，突出混合矩对寿命依赖定价的重要影响。
- 提醒定价过程中依赖结构误判对产品价值带来重要误差风险。

---

3. 重要图表深度解读

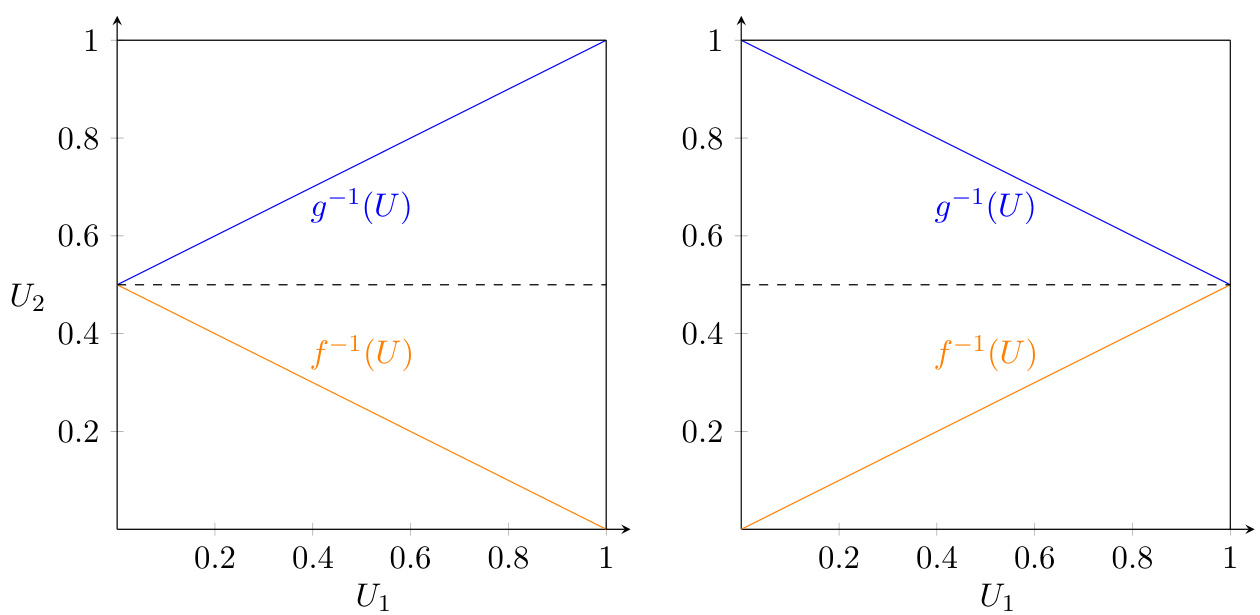
图1（第8页）

• 内容：展示了在$X2$服从对称零均值分布且$d$偶数时，最大化与最小化 $\mathbb{E}(X1 X2^d)$ 的copula支持。

- 趋势：
- 左图（最大支持）中，$U2$围绕中间位置0.5分布，呈线性加权型，对应秩转换函数由$g^{-1}(U)$和$f^{-1}(U)$分片组合形成。
- 右图（最小支持）则呈现相反变换，依赖结构体现出部分逆转的秩相关。

• 联系论点：图形直观展现Theorem 2.1为高阶混合矩界限提供的依赖边界结构，强调了对称分布下的极值策略。

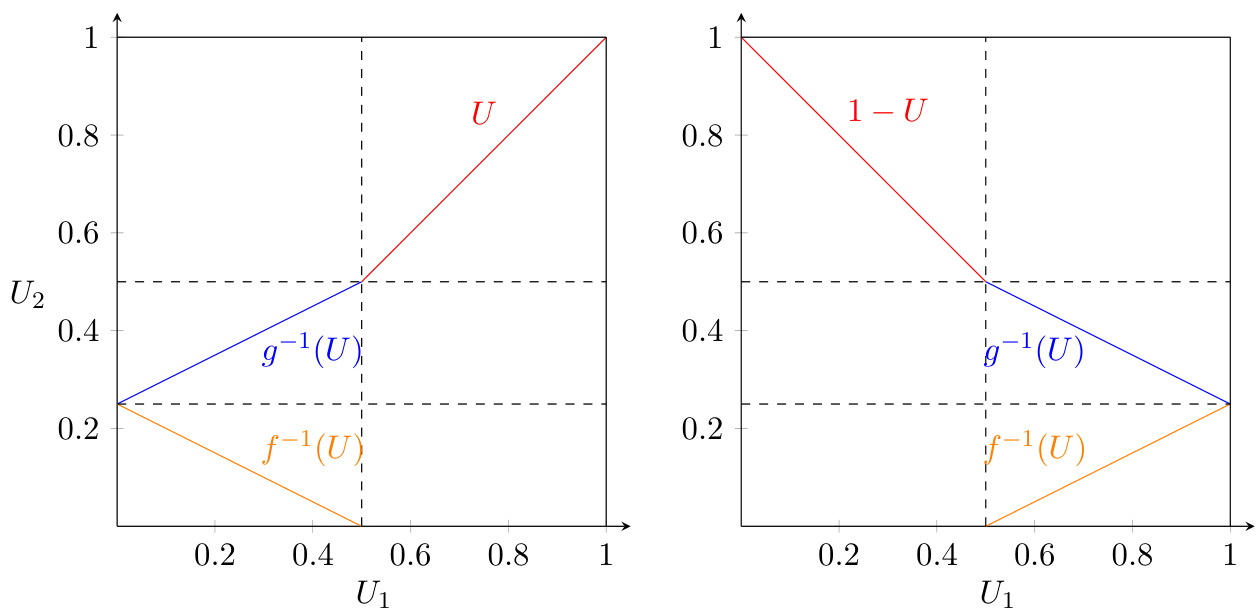
图2（第11页）

• 内容：展示当$X2 \sim U[-1,3]$时，最大化和最小化 $\mathbb{E}[X1 X2^2]$ 的copula支持。

- 趋势：
- $U1$横坐标与$U2$纵坐标对应分块区间，分段线性函数网格结构。
- 最大copula支持中，部分区间呈正相关形态，而最小copula支持则呈部分负相关。

• 联系论点：具体均匀分布示例体现定理中实用的构造方法，凸显混合矩依赖极值的局限与可扩展性。

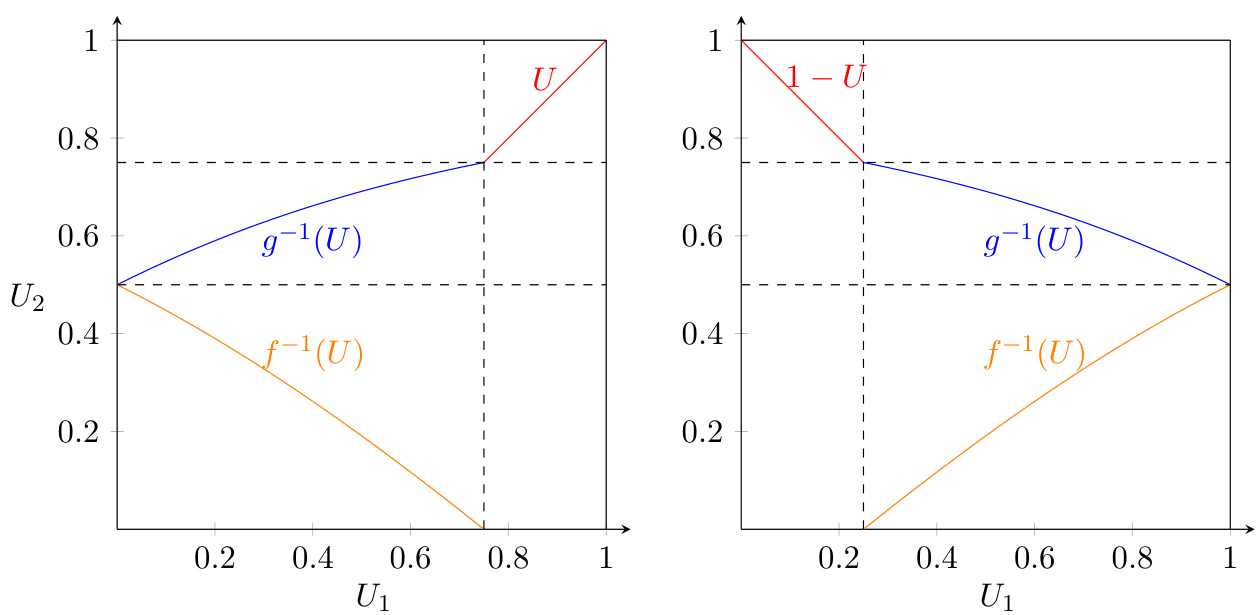
图3（第12页）

• 内容：基于偏移指数分布，展示最大化/最小化 $\mathbb{E}(X1 X2^d)$ 的copula支持。

- 趋势：
- 竖直切割线明确划分了$U$分布区间，体现了混合copula中对$U$分布的依赖。
- $U2$随$U$单调变化呈倒U或U型，分段概率权重由$J$变量控制。

• 意义：图形验证Proposition 2.4及相关计算，彰显实际精算应用中指数分布依赖建模的合理性。

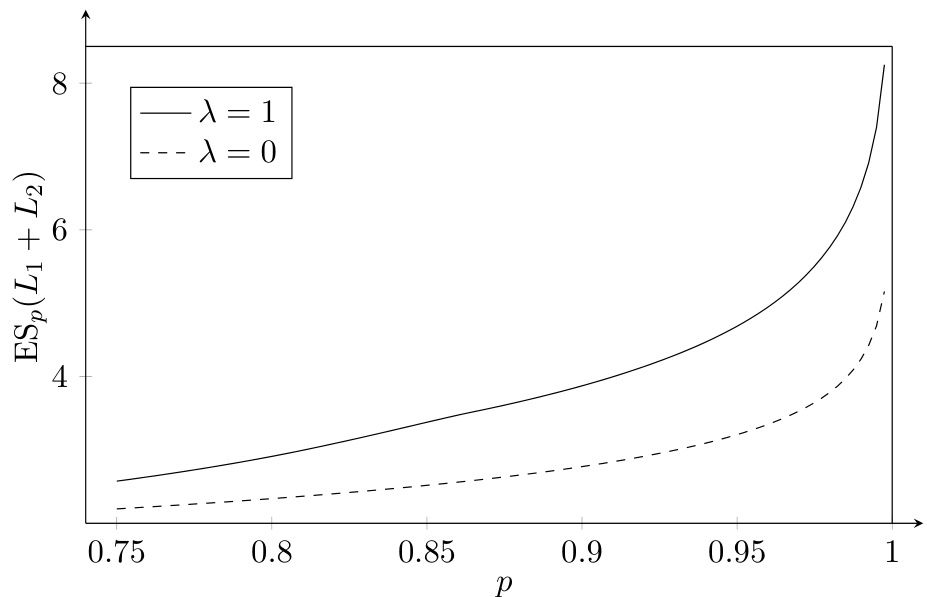
图4（第18页）

• 内容：不同依赖级别（$\lambda=0$ 和 $\lambda=1$）及混合矩极值下，保险组合损失$L1 + L2$的ES随置信水平$p$的变化。

- 趋势：
- ES随$p$递增而增大且两条曲线间隙扩大，说明高混合矩显著提高尾部损失风险。

• 意义：强调高阶混合矩对保险资本要求的实际影响，提供调控风险策略的量化依据。

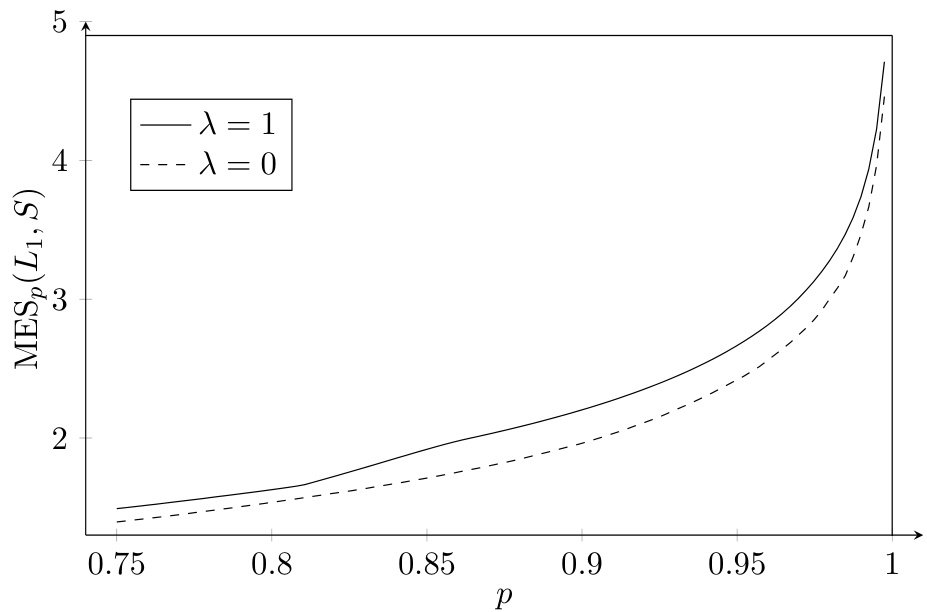
图5（第20页）

• 内容：同上，但为MES，即单一风险$L1$对系统风险贡献随$p$的变化。

- 趋势：
- MES两条曲线差异先增后减，在$p$趋近1时趋于一致，呈现非单调复杂效应。

• 意义：体现MES对混合矩依赖结构的敏感度更复杂，需要谨慎风险分配判断。

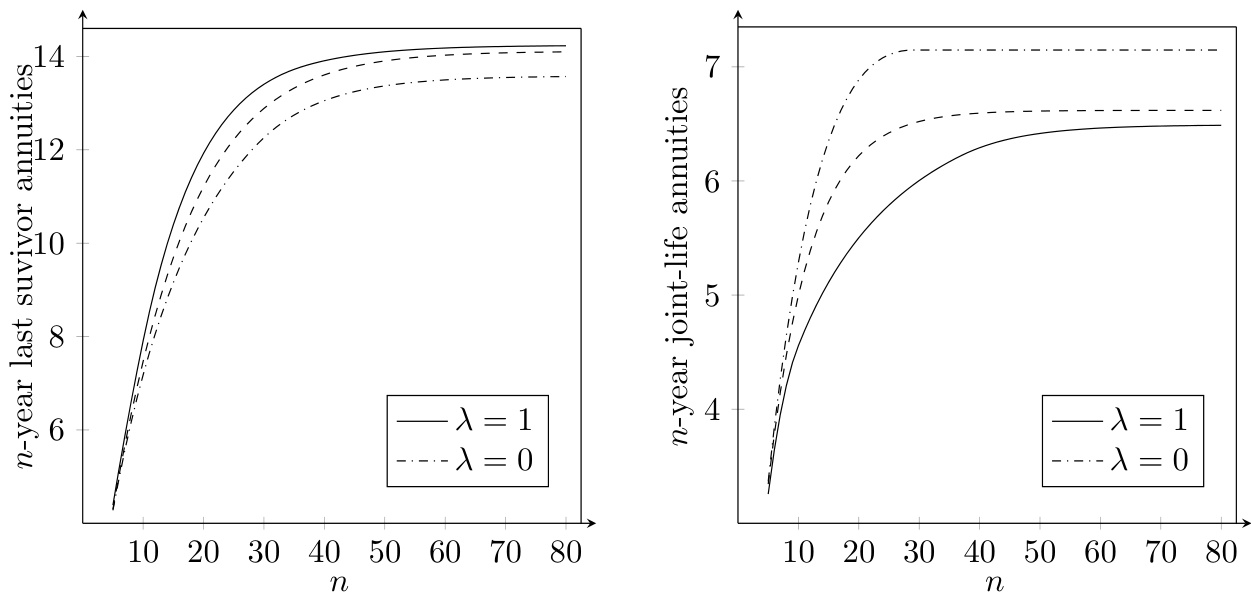
图6（第22页）

• 内容：夫妻寿命依赖不同混合矩极值情况下，$n$年末存和联生年金现值随$n$变化的动态图。

- 趋势：
- 末存年金价值随混合矩增加而升，联生年金则随混合矩增加而降。
- 随年期$n$增长，两类年金价值差异逐渐拉大。

• 意义：定量反映寿命依赖对多生命周期产品定价的影响，提示寿命依赖模型误差的风险。

---

4. 估值分析

本报告估值主要体现在寿命保险年金定价，所用方法包括：

• 基于指数分布寿命模型，利用指数分布的参数$\lambda$估计个体生命长度。

- copula模拟依赖结构，通过混合copula $C\lambda$调整高阶中心混合矩，实现不同依赖相关程度。

• 利用$\,{}t p{x:y, \lambda} = P(\min(Tx, Ty)>t)\,$ 和 $\,{}t p{\bar{x}:y, \lambda} = P(\max(Tx, Ty)>t)\,$ 等函数，折现计算年金现值$ a{\overline{x:y}|\overline{n},\lambda}$和$a{x:y|\overline{n},\lambda}$。

- 蒙特卡洛仿真实现复杂分布与依赖情况下的数值估计。

• 利用加拿大真实数据校准生命参数，增强估值可信度。

该估值框架显然结合了传统概率论（指数寿命模型）、依赖建模（copula）与金融折现估值，属于经典精算方法的现代拓展。

---

5. 风险因素评估

• 依赖结构不确定性：仅已知边际变量分布，无明确信息约束copula，极致情况下尺寸风险度量上下界显著不同。

- 高阶混合矩的影响：不仅影响资本需求（ES）和定价，还影响系统风险贡献（MES），但MES对依赖参数更为敏感且呈现非单调关系。

• 模型误设风险：误判变量依赖结构（尤其寿命相关）可导致重大定价失真，风险资本配置偏差。

- 监管影响：Solvency III与Basel III推荐使用ES等更先进风险度量方法，要求精算和风险管理人员考虑高阶矩和依赖不确定性。

• 提出缓释建议：降低个别业务与整体业务组合的协偏度，可以减轻资本压力，但不能简单以此代替系统风险管理。

---

6. 批判性视角与细微差别

• 报告理论体系严密，数学表达详细，但以下方面值得关注：

- 模型依赖假设：指数边际及特殊copula虽广泛应用，现实中很多保险风险并非纯指数分布，模型的稳健性和扩展性需进一步研究。
- 极值copula实用性：最大化、最小化copula多为理论构造，实际操作时难以完全实现，需结合经验数据确定合理依赖范围。
- MES复杂性：MES对高阶混合矩的影响非单调且依赖参数复杂，报告也显示在某些参数下无显著联系，实际风险管理应用中需结合更多约束信息。
- 风险缓释策略难度：尽管提出降低混合矩为缓释思路，但如何实际调整产品组合以操作混合矩存在较高难度。
- 局限于二维及特定阶次：研究主要针对双变量及整数阶正矩，未来多元高阶混合矩、多样分布的推广尚待深化。
- 部分公式和文字存在排版和表达歧义，在阅读中需要根据上下文解释，但整体逻辑不受影响。

---

7. 结论性综合

本文系统深入地探讨了依赖不确定性下高阶混合矩（$\mathbb{E}(X1 X2^d)$）的理论边界及其在金融精算中的具体应用，重点内容总结如下：

• 理论突破：

- 在已知边际分布但未知依赖情况下，精确求解高阶混合矩的上下界，填补了此类别问题当前研究空白。
- 明确了极值依赖结构的构造方式及其分布函数反演，有效结合了copula理论和极值风险度量。
- 创新提出标准化秩系数$RSd$，实现了高阶混合矩依赖的有界、易解释新指标，扩展了传统相关系数概念。

• 精算应用：

- 探讨了高阶混合矩对期望损失（ES）和边际期望损失（MES）的影响，发现ES与混合矩同向单调但MES受参数影响更复杂，可能不变或非单调。
- 分析了人寿年金定价中寿命依赖表现出的高阶混合矩效应，强调误判依赖结构将导致重要定价误差。
- 实证研究基于指数分布和加拿大人口数据，验证模型实际适用性与参数校准途径。
- 数值模拟（图1-6及对应表格）具体展示了理论结果的实用影响与量化程度。

• 监管与实践含义：

- 监管框架日益重视ES替代VaR，报告结果为风险资本计量和业务组合风险管理提供理论和实操指导。
- 提示实施风险管理时考虑高阶矩依赖，以降低资本压力及避免系统性风险误判。
- 强调高阶混合矩作用重要但复杂，风险度量和资本分配策略应兼顾其非线性特性。

总的来说，报告不仅丰富了高阶矩依赖不确定性理论，还为保险业风险管理及产品定价提供了科学的数学工具与洞见，具备显著的学术价值与实践指导意义。

---

附录：重要图表展示

• 图1：

- 图2：

• 图3：

- 图4：

• 图5：

- 图6：

---

【备注】全文内容和论断均严格取自原文材料，引用均添加了页码溯源标识，确保内容的溯源性与准确性。[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]

报告