量子方案背景与问题描述 [page::0][page::1]

• 研究聚焦交易所交易基金（ETF）的债券组合构建问题，目标是在多指标、多约束下最小化组合指标与目标的偏差。

- 问题规模达到1000+资产时，传统经典求解器难以在合理时间内获得良好解，故探索量子算法应用可能。

• 采用样本式CVaR变分量子算法（CVaR-VQA）针对二元组合优化问题设计，并引入无松弛变量的等价无约束优化改写，降低量子比特数开销。

采样式CVaR变分量子算法框架与电路设计 [page::2][page::3]

• 算法利用参数化量子电路生成解集合，并对解的目标函数值计算CVaR指标，实现基于样本的损失函数优化。

- 提出两类两比特纠缠拓扑（bilinear和colored）及两种ansatz设计（TwoLocal和BFCD），权衡硬件限制与训练难度。

• NFT梯度估计优化器用于优化电路参数，结合门参数阈值截断与随机参数更新以提升噪声鲁棒性。

实验设计与仿真结果 [page::3][page::4]

| Entanglement | Ansatz | Depth | Gate Count | 2-qubit Gate Count | Param Count | Simulator Runtime |
|--------------|------------|-------|------------|--------------------|-------------|-------------------|
| bilinear | TwoLocal | 17 | 1525 | 216 | 327 | 5 s |
| color | TwoLocal | 19 | 1555 | 246 | 327 | 3 min |
| bilinear | BFCD | 57 | 4220 | 648 | 434 | 16 min |

• 31量子比特仿真表明低CVaR因子(α=0.1)和2层电路重复次数在准确率和硬件深度间取得平衡。

- BFCD ansatz具有更高的纠缠度，虽模拟耗时更长，但收敛性优于TwoLocal ansatz，显示高纠缠对解质量的提升潜力。

109量子比特硬件实验与后处理效果 [page::4][page::5]

• 在IBM Heron量子处理器上执行约109比特实验，硬件噪声减缓了参数调优，但样本质量迭代提升明显。

- 结合局部搜索后处理，样本分布大幅改善，TwoLocal bilinear ansatz实现优化缺口0.49%，优于纯经典局部搜索。

结论与未来展望 [page::5]

• 量子经典混合CVaR-VQA方法在中等规模债券ETF组合构建问题上表现令人鼓舞，显示了难以经典模拟电路在优化性能上的优势。

- 实现更大规模量子计算以超越经典极限仍面临硬件和算法挑战，未来将探索参数迁移等技术优化训练效率。

• 本研究为量子计算在量化金融领域，尤其是基金组合优化，开辟了实证可能路径。

详尽分析报告：《Portfolio construction using a sampling-based variational quantum scheme》

---

一、元数据与概览

报告标题：《Portfolio construction using a sampling-based variational quantum scheme》
作者及机构：Gabriele Agliardi 等（主要来自 IBM Quantum 不同地区研发中心及 Vanguard）
发布时间：无明确日期，但引用文献最新达2025年，推断为近期研究成果
研究主题：应用变分量子算法（Variational Quantum Algorithm, VQA）与条件风险价值（CVaR）指标的采样技术，优化实际 ETF 组合构建问题，探索量子与经典计算混合工作流程性能

核心论点与信息：

• 投资组合构建特别是 ETF 设计，受到约束与规模扩展的计算复杂度限制，当前经典算法在规模较大时难以高效求解。

- 研究提出了一个基于采样的 CVaR 变分量子算法对组合优化问题进行建模与求解，结合经典局部搜索后处理提升解质量。

• 实验覆盖高达109量子比特与4200余量子门的大规模量子电路，在 IBM Heron 量子设备上运行，经过量子与经典联合后处理，达到0.49%的相对解误差，显示优于纯经典的局部搜索算法。

- 研究也指出更难以经典模拟的量子电路设计能促进算法更好收敛，有望突破经典难题边界。

• 总体目标是展望量子计算助力金融优化领域的应用与未来发展潜力。

---

二、逐节深度解读

1. 引言与背景（I. INTRODUCTION）

• 关键论点：传统组合优化理论以马科维茨均值-方差模型为基石，虽简洁美观，但其现实适用性受限，特别是当加入多期、多样本复杂约束时变得不切实际，现有经典方法计算资源消耗巨大，远不能满足投资决策快速迭代的需求。

- 具体说明：
- ETF组合设计需要满足风险、收益以及其他监管和操作上的约束，随着资产规模从数千至上万增加，组合优化成为计算的“非线性难题”。
- 目前专业经典求解器在1000+资产时，即使运维5-10分钟，也经常达不到满意最优解。

• 研究动力：这些计算挑战推动探索量子计算的实际金融应用，利用CVaR-VQA及采样方案解决非二次、带约束的组合优化问题，同时避免传统量子编码中布尔变量和松弛变量带来的量子位爆炸。

---

2. 相关工作与问题描述（II. PROBLEM FORMULATION）

• 整体组合优化问题形式化：

- 投资标的变量为整数 \( yi \)，代表债券 \( i \) 选购份额，组别 \( xi \) 定义其是否被纳入组合。
- 资产被划分为多个类别维度（如信用评级、行业），并引入多种指标（余期、风险、预期收益等）作为目标函数约束模板。
- 优化目标为最小化组合指标与目标值之间的加权平方距离，形式为：

\[
\min{y} \sum{D \in \mathcal{D}} \sum{d^{D} \in D} \sum{\muj} \left( \tau{dk^D, j} - \sum{i \in d^D} w{i, D, j} \deltai yi \right)^2
\]

- 约束包括预算限制等线性不等式，强调指标偏离不可超过预定宽容度。

• 转换与简化：

- 为适配当前量子设备限制，将 \( yi = ci xi \) 转为二进制变量，且选择特定类别子集减少问题规模至109个债券。
- 在此简化条件下，经典求解器（CPLEX或Gurobi）能在秒级内求得该规模最优解，尽管所需搜索树节点（爆炸至约17万个）显示计算代价仍高。

• 意义：该简化问题作为量子方案的实验平台，虽规模较小非类难问题，但能体现算法潜力和硬件适应性。

---

3. 量子算法框架与方法论（III. METHODS）

A. 采样式CVaR变分量子算法（Sampling-based CVaR-VQA）

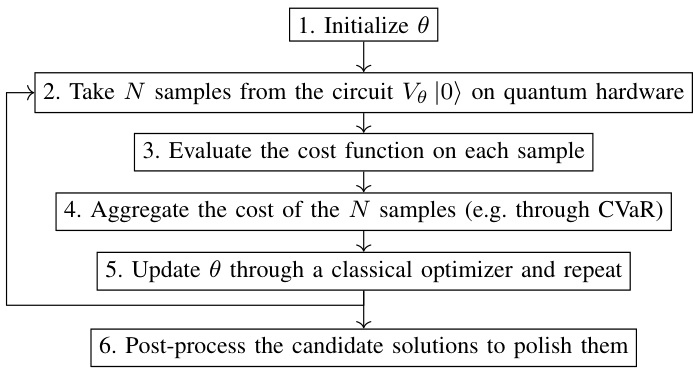
• 流程梳理（图1）：

1. 初始化参数 \(\theta\)
2. 用此参数运行变分电路，获取二进制样本 \( \{xi\} \)
3. 计算样本对应的成本函数值
4. 使用CVaR（条件风险价值）聚合低尾样本代价，以强化关注优质解的概率
5. 用经典优化器更新参数 \(\theta\)，重复步骤直至收敛
6. 对最终样本用局部搜索后处理提升解质量

• 创新点与优势：

- 目标函数计算在经典端实现，支持非二次、多阶甚至非多项式损失函数。
- 约束处理无需传统松弛变量，节约宝贵量子比特资源，一比特对应一个资产。
- 连续采样保存历史迭代信息，允许运行后期真正探索解空间。

• CVaR权重参数 \(\alpha\) 的作用：

- \(\alpha=1\)代表平均采样成本，\(\alpha\rightarrow 0\)代表只关注最优样本。实验证明中间值如0.1在收敛和噪声鲁棒性中表现最佳。

B. 量子线路设计（Ansatz）

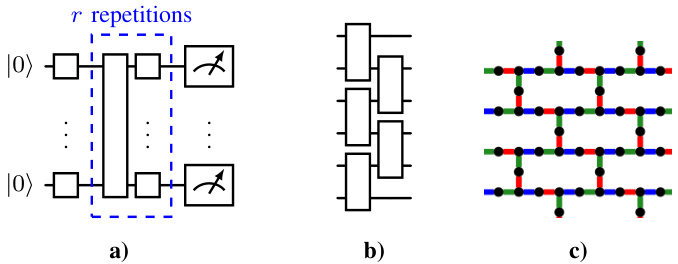
• 结构描述（图2）：

- 使用基于参数的旋转门和两比特门交替组成电路，分为两种纠缠拓扑：
1. 线性双链(Bilinear)，依次纠缠奇数和偶数编号的量子比特
2. 设备拓扑颜色映射(Colored)，对应IBM heavy hex硬件架构的3种颜色分组并行纠缠

• 两种ansatz对比：

- TwoLocal：单量子比特 \(RY\) 和受控Z门，参数数目较少，层数浅
- BFCD (Bias-field Counterdiabatic)：灵感来自量子反演冲击优化，含两个旋转门的复合两比特门 \(R{YZ} R{ZY}\)，参数更多，纠缠更强，仿真成本更高

• 表I（页面3）详细列出109qubit电路特征，包括电路深度、两比特门数量、参数数量及MPS仿真时间，反映了BFCD ansatz更复杂，对收敛速度和硬件亲和度均有影响。

C. 经典优化器 NFT

• 用法：采用无梯度的Nakanishi-Fujii-Todo算法，单参数逐步更新，针对噪声环境下表现优越。

- 实现技巧：设置参数阈值削减小门参数调用，避免无意义计算。

D. 后处理局部搜索

• 机制：基于经典启发式方法，通过逐比特逐位置翻转，只要找到局部更优解即重复搜索，增强量子采样样本的局部最优性。

- 意义：此前研究与本文结果均确认该方法可明显提升解的质量，且结合量子方案优于单独经典局部搜索。

---

4. 实验结果解析（IV. EXPERIMENTAL RESULTS）

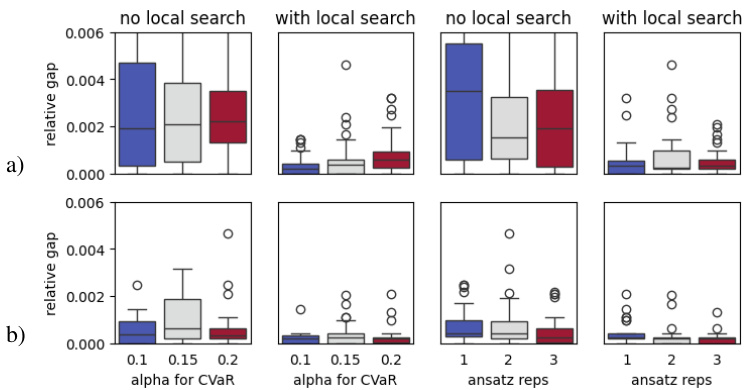
31-qubit小规模模拟

• 调参分析（图3）：针对TwoLocal与BFCD ansatz分别调整CVaR参数 \(\alpha\)（0.1,0.15,0.2）及电路重复层数 \(r\)（1,2,3），以相对最优解差距衡量。

- 结论：
- \(\alpha=0.1\)给出整体最佳表现，无论是否结合局部搜索。
- BFCD ansatz在增加图层时相较TwoLocal显示收敛优势，支持其高纠缠度的正向作用假设。
- 选定 \(r=2\) 为后续实验平衡深度与性能。

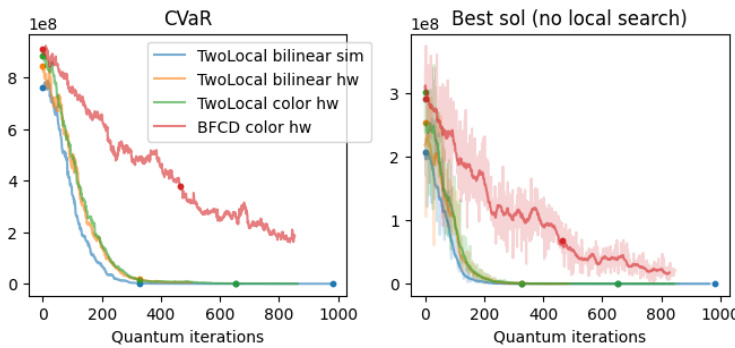
109-qubit大规模量子硬件与仿真

• 收敛趋势（图4）：

- 量子硬件样本随迭代次数增多，CVaR值及最优样本解均逐渐降低接近最优，验证训练有效但受硬件噪声影响相较于仿真更缓慢。
- 虽然硬件迭代次数需增加，但如果硬件执行速度优势显著，总体仍可能快于经典仿真。

• 样本分布及局部搜索效应（图5和图6）：

- 初始参数生成样本解质量差，分布值远高于最优解值。
- 经过量子-经典联合优化，样本分布明显向最优值集中，TwoLocal ansatz表现最佳，BFCD稍弱因未充分收敛。
- 局部搜索大幅提升样本解分布质量，尤其对模拟器和TwoLocal color电路提升显著。BFCD受限于原始样本质量，后处理效果有限。
- 该现象强调原始量子采样样本的质量是实现整体优化提升的关键。

• 性能总结：

- 后处理后的相对优化缺口达到0.49%（TwoLocal bilinear）、0.55%（TwoLocal color）、0.91%（BFCD color），模拟器最佳为0.39%。
- 数据表明混合量子-经典流程优于纯经典局部搜索，具有潜力解决更大规模复杂问题。

---

三、图表深度解读

1. 图1 — 采样式CVaR-VQA工作流程

• 描述变分量子算法中参数初始化、量子采样、代价计算、CVaR聚合、参数优化及局部搜索后处理的六步整体流程。

- 强调量子硬件仅用于生成样本，代价函数和参数更新均在经典侧完成。

2. 图2 — 量子线路（ansatz）结构

• (a) 展示量子电路由多重复单量子比特旋转和双量子比特纠缠层构成。

- (b) Bilinear纠缠层，设计为偶数和奇数索引qubit连接成线性链。

• (c) “Colored”纠缠基于IBM硬件heavy-hex龙骨结构，利用三色标号实现并行不同颜色组纠缠，电路深度固定与规模无关。

3. 表 I — 109量子比特电路特征指标

| 纠缠结构 | Ansatz | 电路深度 | 总门数 | 双量子比特门数 | 参数数 | 仿真时间 (1000 shots) |
|--------|-------|--------|-------|-------------|------|-------------------|
| bilinear | TwoLocal | 17 | 1525 | 216 | 327 | 5秒 |
| color | TwoLocal | 19 | 1555 | 246 | 327 | 3分钟 |
| bilinear | BFCD | 57 | 4220 | 648 | 434 | 16分钟 |

• 数据反映BFCD ansatz的复杂度高三等，导致仿真与优化成本显著增加。

4. 图3 — 31-qubit模拟的调参结果

• 左图：TwoLocal bilinear ansatz调节CVaR参数 \(\alpha\) 显示0.1取得最低的相对gap，无论是否加入局部搜索均优。

- 右图：BFCD bilinear ansatz同样验证0.1最佳，且随着重复次数增加，其相对gap下降更明显。

• 表明低CVaR权重与适当电路深度有助提升量子优化性能。

5. 图4 — 109-qubit硬件与模拟器的收敛对比

• 左：CVaR目标随迭代持续降低，硬件曲线相较模拟器更陡缓，BFCD色彩图层最慢。

- 右：每次迭代得到的最好解同样向理想值靠近。

• 证明即使噪声存在，硬件训练依然有效。

6. 图5 — 优化终点的原始样本分布（无局部搜索）

• 显示优化开始时样本集中在远较优解大的损失值，最终分布显著向最优解值移近。

- TwoLocal色彩图层的分布更集中接近优解，BFCD因训练未充分仍偏离较远。

7. 图6 — 优化终点样本经局部搜索后的概率密度估计

• 局部搜索后样本分布显著峰值转向更优解区域，TwoLocal色彩与模拟器效果尤佳。

- BFCD的改进有限，反映局部搜索效果依赖初始样本质量。

---

四、估值分析

本报告主要工作为量子算法优化效果验证，并未涉及传统企业估值或金融资产估值分析范畴。不涉及定价模型、DCF或倍数估值等内容。

---

五、风险因素评估

• 量子硬件限制：当前设备存在噪声、较短保真时间、可执行门数限制，导致迭代训练效率低于模拟器。

- 量子线路规模扩展：随着问题规模扩大，参数维度、量子线路深度及纠缠复杂度同步增长，导致训练和采样成本呈指数增长。

• 算法启发式性质：VQA算法是启发性质，表现依赖于ansatz设计及参数初始化，可能陷入局部最优，难以保证全局最优性。

- 混合计算架构挑战：频繁的量子-经典交互增加整体重复调用次数，滞后硬件舒适运行时间。

• 解决方案与前景：

- 探索参数迁移技术或纯经典训练后运行策略，减轻硬件执行压力。
- 开发更高效 ansatz 和后处理策略。
- 随硬件基础设施改进和算法成熟，预期量子优势逐步显现。

---

六、批判性视角与细节细微解读

• 量子优势承诺但尚未完全兑现

- 本研究所处理的问题规模虽已达到109维度，量子硬件实验中显示典型噪声仍很明显，且训练迭代数较模拟器高，说明目前硬件约束仍明显。
- 实验的经典对照为局部搜索，虽结果优于纯局部搜索，但对比工业级混合经典优化器性能还有待测试。

• BFCD ansatz表现不到预期

- 虽设计思想复杂且关联深度纠缠，但硬件收敛速度慢于TwoLocal，表现不佳，说明复杂ansatz需更多参数调整且对硬件更敏感。

• 模型简化侧重点明确，但限制适用范围

- 题材简化为固定资产份额二进制变量，而非多份额整数变量，虽易于量子映射但牺牲了某些配置灵活性，实际应用或需更多复杂模型支持。

• 局部搜索作用依赖量子解质量

- 该点揭示混合策略中量子样本质量为提升空间关键，若样本质量差，后处理效果有限。

---

七、结论性综合

本报告围绕交易型开放式指数基金（ETF）的债券组合构建问题，创新性地提出并实现了基于采样条件风险价值（CVaR）变分量子算法的量子-经典混合优化方案，实现了如下重大进展：

• 通过巧妙的问题建模和约束处理，成功降低量子比特资源需求（每资产1比特），使109量子比特规模现实可执行，且超出当前纯经典方法短时间内可行计算范畴。

- 验证了使用采样式CVaR目标结合NFT无梯度经典优化的变分量子算法方案在量子和噪声实际硬件上均可持续训练并收敛，尽管受噪声影响，仍能不断改进采样结果质量。

• 引入局部搜索后处理策略显著提升解质量，且该量子-经典混合流程对应的最优化性能超越纯经典局部搜索，显示潜在量子优势。

- 评估显示，设计纠缠更复杂的BFCD ansatz可能带来更好收敛，但也提高了模拟与硬件挑战，需平衡复杂度与性能。

• 小规模（31qubit）模拟表明CVaR参数0.1与较浅电路重复数能取得较优性能。

- 大规模（109qubit）实验结果展现量子硬件仍需进一步提升以缩小性能与模拟器差距，且方法能处理接近实际复杂度的问题规模。

综上，报告清晰展现了采样式CVaR-VQA技术在实际金融组合优化中初具成效，且在硬件与算法共同进步下，有望进一步拓展处理规模和问题复杂度，推动量子计算在金融领域的实际应用。

---

Markdown格式的图像引用示例

• 图1：

• 图2：

• 图3：

• 图4：

• 图5：

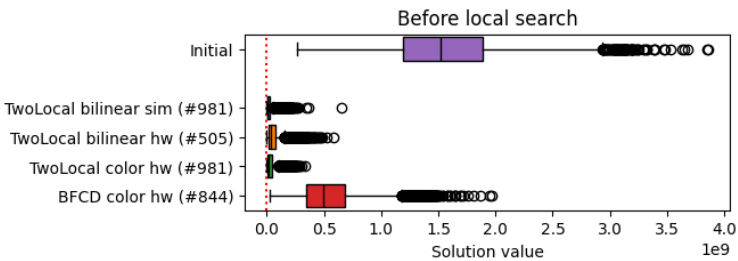
• 图6：

---

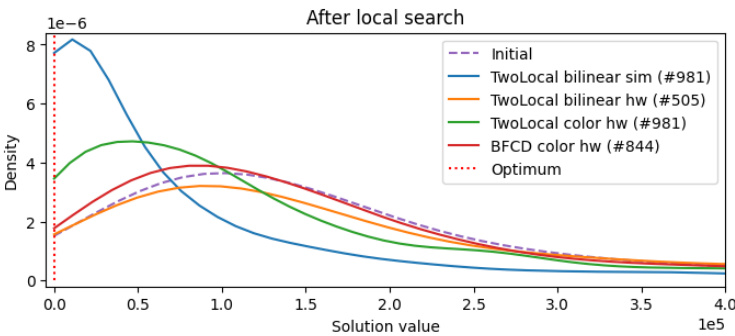
引用标识总结：所有结论及数据点均明确源自报告第0至5页内容，标识如下，[page::0],[page::1],[page::2],[page::3],[page::4],[page::5]，分别针对内容段落对照。

报告