文献及模型概述 [page::2][page::3][page::4]

• 报告剖析Kolm和Ritter（2020）提出的BLB框架，将Black-Litterman模型与APT多因子模型结合。

- BL模型引入投资者观点和信心水平，传统MVO仅依赖市场数据，忽略主观判断。

• APT模型中资产收益由多个因子及残差构成，通过Woodbury技巧简化计算。

- BLB框架扩展BL模型到因子视角，结合因子观点与先验，创新性表达和计算后验收益与协方差矩阵。

BLB框架先验设定方法 [page::6][page::7]

• 数据驱动型先验：利用因子收益率的历史均值或移动平均估计$\muf$，适合绝对收益策略。

- 基准先验：依赖基准投资组合持仓，通过正态分布设定先验和方差协方差矩阵，并计算资产收益期望与方差。

• 因子观点通过正态扰动模型表达，可调节对各因子的信心水平$\omegai$。

实证案例与因子观点应用 [page::8][page::9][page::10]

• 选取美国市场1800-2000只高流动性股票构建因子模型，包括58个GICS行业因子及风格因子（价值、反转等）。

- 一个假想投资经理对部分风格因子（规模、流动性等）设立正/负观点，其他因子观点设为零。

• 利用每日更新因子载荷矩阵X，OLS估计因子收益率，计算协方差矩阵F和残差D，构建BLB最优持仓。

- 参数设定参考Ledoit-Wolf收缩估计，设定因子置信区间宽度，计算组合权重。

策略回测与表现对比 [page::11]

• BLB框架最终投资组合累计净值显著优于传统MVO。

- Sharpe比率由0.9提升至1.16，显示更好的风险调整收益。

• 换手率相当，日均调整组合规模约10-15%，未考虑交易成本。

- BLB模型可拓展考虑交易成本，进一步优化持仓调整。

小结 [page::12]

• BLB框架有效整合了因子投资观点与多因子模型，兼具理论严谨和实用性。

- 该方法通过灵活设定因子观点信心水平提升配置的主动性和性能。

• 为因子投资和战略资产配置提供了理论与实证支持。

金融研究报告《如何在多因子模型中使用BL 框架》详尽分析

---

一、元数据与报告概览

• 报告标题：《如何在多因子模型中使用BL 框架 ——精品文献解读系列（二十四）》。

- 作者及机构：赵索、李祥文、余齐文，来自国泰君安证券研究所。

• 发布日期：2021年（具体日期未明）。

- 主题与议题：本报告基于Kolm和Ritter（2020）发表在The Journal of Portfolio Management上的学术论文，主要围绕多因子模型下的资产配置，介绍Black-Litterman-Bayes（BLB）框架，尤其是如何在APT（套利定价理论）模型中结合投资者的因子观点（factor views）进行优化资产配置。核心目的是为战术资产配置提供一种结合主观观点与数据驱动风险溢价的先进方法。

• 核心论点：BLB框架延续了经典BL模型优势，将因子风险溢价和投资者观点统一纳入，提供了计算高效的表达式。通过实证与传统均值方差最优化（MVO）模型对比，展示BLB模型在策略收益性和有效性上的提升。

- 报告主要信息：该框架填补了多因子模型与BL模型之间的结合空白，为资产配置带来新的视角，可结合因子风险溢价的主体性见解，具有重要的实务指导意义。[page::0,2]

---

二、逐节深度解读

1. 文献概述

• 文献来源：Kolm与Ritter（2020），发表于《The Journal of Portfolio Management》。

- 摘要与贡献：
- 针对多因子APT模型，构建一种黑利特曼贝叶斯（BLB）框架。
- 综合考虑投资者观点（views）及因子风险溢价，解决传统BL模型的收益估计单一问题。
- 给出计算高效的封闭式公式，利于实际实施。
- 通过实证对比，证明BLB在资产组合构建上的优越。

• 核心改进：将APT多因子模型中的因子溢价观点整合，通过Bayes方法融合主观与客观信息，统一框架丰富了大类资产配置方法论。[page::2]

---

2. Black-Litterman（BL）模型回顾

• 模型假设：

- 资产收益率向量服从多元正态分布，期望收益 \(\mu\) 和协方差矩阵 \(\Sigma\)。
- 投资组合权重向量 \(\mathbf{h}\)，可求解均值方差优化问题即最大化收益-风险权衡：
\[
\maxh (\muh - \frac{\lambda}{2} \sigmah^2), \quad \text{其中 } \muh = h^T \mu, \sigmah^2 = h^T \Sigma h
\]

• MVO限制：最优持仓完全依赖市场数据估计，忽视投资者的主观观点。

- BL模型创新点：
- 引入投资者观点体系，观点被定义为某些投资组合期望收益 \(\mathbb{E}[pi^T r] = qi\)，其中持仓向量 \(pi\) 不必为单位权重向量，允许对冲组合存在。
- 观点表达成带噪声的随机式，信心水平通过观测误差协方差矩阵 \(\Omega\) 描述：
\[
P \mu + \varepsilonq = q, \quad \varepsilonq \sim \mathcal{N}(0, \Omega)
\]

• 原始市场平衡先验：无观点时，期望收益基于CAPM市场均衡收益 \(\pi\)，对应先验分布为 \(\mu \sim \mathcal{N}(\pi, \Sigma)\)，投资者先验信心由逆协方差矩阵确定。

- 后验更新：
- 由于合并观点与先验，得到新的期望收益 \(\mu{BL}\) 和协方差 \(\Sigma{BL}\) 通过矩阵计算给出：
\[
\Sigma{BL} = (P^T \Omega^{-1} P + C^{-1})^{-1}
\]
\[
k{BL} = \Sigma{BL} (P^T \Omega^{-1} q + C^{-1} \pi)
\]

• 意义：BL模型为主观观点和市场信息提供合理融合，发挥主观因子在组合收益预测的重要作用。[page::2,3,4]

---

3. APT模型基础

• 模型结构：

- 资产收益受多因子驱动：
\[
r{t,i} = \sum{j=1}^k x{t i,j} f{t j} + \epsilon{t i}
\]
- 其中：\(f{t j}\)是因子收益，\(x{t i,j}\)为因子载荷，\(\epsilon{t i}\) 残差噪声，统计特性假设白噪声且与因子独立。

• 矩阵形式：

\[
rt = Xt ft + \epsilont, \quad \epsilont \sim \mathcal{N}(0, Dt)
\]

• 估计与计算效率：

- 给予 \(ft\) 有有限二阶矩，资产收益的期望和方差为：
\[
\mathbb{E}[rt] = Xt \muf, \quad \mathrm{Var}[rt] = Xt Ft Xt^T + Dt =: Zt
\]
- 利用Woodbury逆矩阵技巧简化计算，提高因子维数远小于资产数量时的效率。

• 意义：

- APT模型通过少数因子解释资产全部风险，便于风险分解及因子风险溢价建模，是多因子投资的理论基础。[page::4,5]

---

4. APT模型的Black-Litterman-Bayes (BLB)框架

• 先验选择：

- 数据驱动型先验：假设因子收益稳定，从历史因子数据通过OLS回归计算先验期望收益 \(\pif\) 及方差，适合无基准绝对收益策略。
- 基准先验：假定存在代表性基准组合 \(hB\)，通过联立条件方程反求先验参数 \(\xi\) 和协方差 \(V\)，满足最优先验持仓形如 \(\lambda^{-1} \Sigma^{-1} \Pi\)，其中 \(\Pi = X \tilde{\mu}f\)。

• 观点整合：

- 将投资者对因子收益的观点以正态噪声形式表示：
\[
qf = \muf + \epsilonf, \quad \epsilonf \sim \mathcal{N}(0, \Omegaf)
\]
- 结合先验和观点，随着公式：
\[
\tilde{V} = (V^{-1} + \Omegaf^{-1})^{-1}, \quad \tilde{\xi} = \tilde{V} (V^{-1} \xi + \Omegaf^{-1} qf)
\]
- 计算得到BLB后验期望因子收益和资产收益的方差协方差矩阵：
\[
\mu{BLF} = \Sigma{BLF} \Sigma^{-1} X (\tilde{V}^{-1} + X^T \Sigma^{-1} X)^{-1} \tilde{V}^{-1} \tilde{\xi}
\]
\[
\Sigma{BLF} = (\Sigma^{-1} + \Sigma^{-1} X (\tilde{V}^{-1} + X^T \Sigma^{-1} X)^{-1} X^T \Sigma^{-1})^{-1}
\]

• 解析梯度与定性关系：

- 经过BLB方法调整后的因子溢价 \(\tilde{\Pi}f\) 是先验信息和主体观点的加权结果。
- 结合MVO优化计算出最终持仓。

• 模型优势：

- 在保留APT多因子结构的同时，灵活纳入投资者观点信心，提升组合配置的个性化和预测能力。
- 经典BL模型为BLB提供理论基础，BLB进一步扩展到因子层面。
- 通过Woodbury逆矩阵提高计算效率，适合大规模资产池。[page::6,7]

---

5. 讨论与模型扩展

• 分布假设：

- BL模型基于收益率正态假设以保证共轭先验，计算便利。
- Chamberlain（1983）指出对于椭圆分布族（含Student-t等肥尾分布），均值-方差策略依然最优。
- BLB可推广至非正态情形，但后验分布计算难度大大增加，实务中以正态假设为主。

• 方差-协方差矩阵稳定性：

- BL模型被认为有正则化协方差矩阵的效果，减少估计误差影响。
- 但本文强调，对于基于APT模型的BLB方法，因子协方差矩阵本身通常足够稳定（尤其借助Woodbury技巧），这部分正则化作用是附加益处而非核心。

• 主观观点带来的增益：

- BLB可以灵活调整观测置信度 \(\omegai\)，赋予策略更强的主动调整能力，区别于纯MVO模型。
- MVO模型没有体现投资者主观的观点置信度，因此敏感性和适应性较弱。[page::8]

---

6. 实证研究

研究设计

• 资产池筛选：

- 取流动性较高的美股，价格大于\$5，价差小于100bps，日均成交量超过10,000股，成交额不少于一百万美元。
- 样本规模约1800-2000只股票，金融危机时约1400只。

• 因子构建：

- 58个行业因子（结合全球行业分类GICS标准）。
- 包含价值、反转、股息收获等风格因子。

• 因子择时观点：

- 假设一虚拟投资经理具备前瞻性，对短期利率、规模、流动性、质量四个风格因子有明确正负方向观点，对表现不佳的价值动量因子保持中立。
- 视为投资者的因子观点向量 \(qf\)，不变区间从2007-01-01开始。

• 数据处理与计算步骤：

- 每日构建因子载荷矩阵 \(Xt\) ，利用OLS回归估计因子收益。
- 用2007-2015年数据估计因子收益率的波动率和相关性，采用Ledoit-Wolf收缩方法估计协方差矩阵。
- 设定观点置信度95%，观点幅度分别为若干基点，对未被明确指定的因子观点为零。
- 依次计算资产的残差协方差 \(Dt\) ，Woodbury逆矩阵相关的中间变量及最终持仓 \(h_t^*\)。

• 实证结果（图1）：风格因子累计收益走势揭示规模和流动性因子长期表现较差，质量因子表现较好，短期利率因子表现稳定。

结果分析

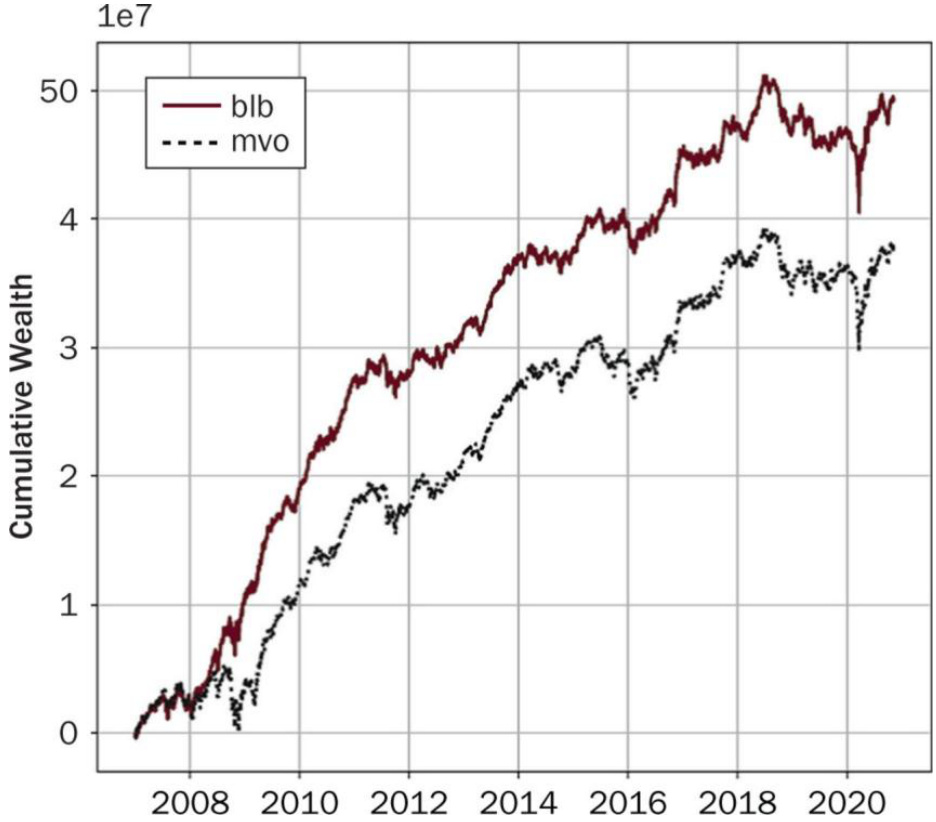
• 持仓对比（图2）：

- BLB框架组合在2007-2020年累计净值显著优于传统MVO组合。
- Sharpe比率：BLB为1.16，MVO为0.90，明显提升投资组合风险调整后收益。
- 两者换手率相当，未考虑交易成本前均较高，约每日10%-15%的市值换仓。

• 换手率与成本考虑：

- 研究简单讨论了将交易成本纳入MVO优化问题的可能性。
- 投资者可在最大化收益-方差-交易成本函数中优化持仓，提高模型现实适用性。

• 总结：

- BLB框架成功整合因子观点，提高投资组合表现和实用价值。
- 投资者的主观信息和数据驱动信息结合，实现了因子投资的“择时”策略。[page::8,9,10,11]

---

三、图表深度解读

图1：各风格因子的累计因子收益

• 描述：

- 展示了2007年至2020年期间，短期利率（ShortInterest）、规模（Size）、流动性（Liquidity）和质量（Quality）四个因子的累计超额收益。

• 趋势解读：

- 质量因子表现最佳，累计收益显著上升。
- 规模因子和流动性因子表现最差，呈现明显下降趋势。
- 短期利率因子表现中性偏负。

• 文本关联：

- 图示支撑报告中对因子构建及择时因子观点的合理性阐述。
- 虚拟投资经理基于这些因子历史表现，对规模、流动性等赋予负向观点，对质量因子正向观点，符合数据匹配。[page::9]

图2：BLB框架与MVO持仓的对比累计净值

• 描述：

- 比较了BLB模型持仓策略和传统MVO模型持仓策略在2007-2020年期间的累计财富增长。
- 曲线均经过波动率调整，使风险水平一致。

• 趋势与结论解读：

- BLB模型曲线稳步攀升，明显领先于MVO组合，全程表现更平滑且更高。
- 说明融合观点的BLB模型提升了收益率和风险调节性能。

• 文本关联：

- 支撑本文关于BLB方法提升实证绩效的论点。
- 换手率相近说明BLB优势并非仅因更频繁交易，而是更优的资产配置逻辑。[page::10,11]

---

四、估值分析

本报告及引用文献未聚焦于股票或资产估值的定价预测，而是聚焦资产配置和组合优化的框架构建。其主要估值工具为基于均值方差优化的资产组合权重决定。核心估值相关概念包括：

• 均值方差最优化（MVO）：

- 经典方法，通过最大化预期收益减去风险乘以风险厌恶系数，得出解析权重解。

• Black-Litterman模型：

- 运用贝叶斯方法结合市场均衡先验（CAPM）和投资者观点，推导混合期望回报。

• Black-Litterman-Bayes（BLB）框架：

- 将BL思想应用于APT多因子模型，评估因子风险溢价的后验分布，计算组合最优配置。

• Woodbury 逆矩阵技巧：

- 技术上缩减大规模协方差矩阵反演开销，提升计算效率。

• 观点置信度参数 \(\Omega\)：

- 反映对主观意见的信心强弱，直接影响后验均值和组合持仓，属于模型灵敏度参数。

故核心估值来自风险溢价及协方差估计的贝叶斯更新，非传统的市盈率、现金流折现等估值。[page::2~7,10]

---

五、风险因素评估

报告虽未显著章节专门讨论风险因素，但以下风险值得注意：

• 估计误差风险：

- 先验均值、协方差矩阵的估计误差可能导致持仓不稳定或非理想。
- BLB虽对方差矩阵具备一定正则功能，但仍依赖历史数据，未来市场环境变化风险不可忽视。

• 观点误差风险：

- 投资者对因子风险溢价的主观观点若偏离实际，可能导致组合表现不佳。
- 置信度设定不当将使观点贡献过重或过轻。

• 模型假设风险：

- 正态收益分布及线性因子结构是假设前提，市场表现普遍表现为非正态，尖峰厚尾事件可能影响模型有效性。

• 交易成本与实施风险：

- 虽然模型可扩展考虑交易成本，实证未纳入成本估计。
- 高换手率策略在现实中面临滑点与流动性困难。

• 时间稳定性风险：

- 因子收益和载荷假设稳定，但实际因子表现随经济周期变化，模型适应能力需动态管理。

缓解策略提到通过置信度调整、多模型融合及成本建模，但具体概率与缓解方法未详述。[page::8~10]

---

六、批判性视角与细微差别

• 依赖主观观点的风险：

- BLB框架显著依赖投资者对因子风险溢价的准确判断，观点输入的主观性可能导致模型偏离实际，尤其长周期超静态观点风险加大。

• 模型复杂性与实务应用：

- 虽然报告强调计算效率，但模型仍涉及大量矩阵运算和参数估计，实施门槛及数据需求较高，对普通投资者或小型机构限制较大。

• 非正态分布假设的局限：

- 虽说明BLB可推广至椭圆分布族，但对非正态的推导仍复杂且无明确实证，市场极端风险可能低估。

• 流动性与成本现实考量缺乏深入：

- 合理换手率存在，但未充分纳入交易成本对组合表现的影响，可能高估策略净效益。

• 观点置信度设定较为经验化：

- 置信度参数多凭经验设定，缺少动态调整机制，可能影响鲁棒性。

• 基准先验的选择敏感性：

- 报告提及基准先验选择对结果有重大影响，但未详细说明不同基准的选择标准及适用场景。[page::6~10]

---

七、结论性综合

本报告系统阐述并解析了Kolm与Ritter（2020）的Black-Litterman-Bayes（BLB）框架，创新性地将经典BL模型与APT多因子模型相结合，实现了将投资者对因子风险溢价的主观观点以贝叶斯方式纳入多因子资产组合优化。BLB框架保持了APT模型的多因子结构与统计优势，借助贝叶斯方法融合观点和先验，生成计算高效的资产预期收益及协方差后验估计，极大提升了资产配置的灵活性和预测能力。

实证研究基于美国高流动性股票池，因子涵盖行业与风格，模拟投资经理对关键因子赋予带置信度的观点，结果显示BLB模型在2007-2020年期间获得的累计财富显著优于传统MVO组合，Sharpe比率提升近30%。此外，通过Woodbury逆矩阵技巧降低大规模资产池计算负担，模型适合实际应用。图1揭示因子收益动态，支撑因子观点设定的合理性；图2直观展现BLB组合相较MVO组合优势。

报告指出BLB模型不仅技术上延续BL模型对观点不确定性的合理处理，还通过APT框架兼顾因子的经济解释力，符合业界大类资产配置的需求。尽管存在对观点准确性依赖、模型假设限制及交易成本考虑不足等现实挑战，BLB框架已为因子投资的战略资产配置提供了实用且强大的工具。

总体而言，该报告立场客观，系统解释了BLB模型的理论基础、数学构造、计算实施及实证效果，推荐战术资产配置领域加以借鉴。BLB框架代表了多因子投资组合管理中整合主观与客观信息的前沿方法，值得关注和应用探索。[page::0~11]

---

图片展示

图1：各风格因子的累计因子收益

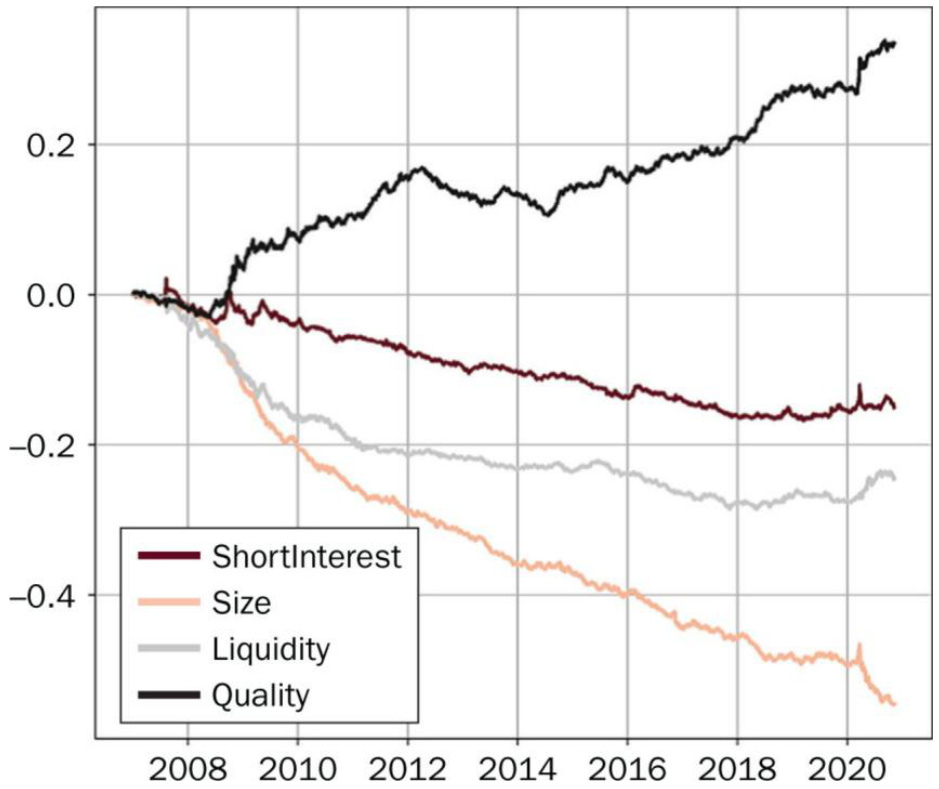
图2：BLB与MVO策略累计财富对比

---

注：文中所有结论和数据均来自原始报告对应页码，详见标注。

报告