目标型均场博弈模型构建与解法 [page::4][page::6]

• 代理人状态动力学为受控布朗运动，代价函数含控制成本和与$\alpha$-分位数目标的二次偏差。

- 通过随机极大值原理导出最优控制，构造前向-后向ODE（FBODE）刻画均场一致性条件，存在唯一解保证ε-纳什均衡。

• 最优策略为状态线性反馈，状态服从高斯分布，均场分位数由均值和方差闭式表达。

阈值型均场博弈模型及数值求解方案 [page::13][page::14][page::15]

• 终端代价为超出分位数阈值以下状态的二次惩罚，无解析解。

- 固定$\alpha$-quantile后通过FBSDE求解最佳响应，迭代求解均场一致性，即分位数自洽方程。

• 提出收敛判定的数值迭代方案（图1）辅助确定均场分位数。

早期风投应用及数值实验分析 [page::15][page::16][page::17][page::18][page::19][page::20]

• 设定创业公司市场价值动态模型，考察不同分位数（如0.95）下的竞争结果和均衡行为。

- 阈值型模型下，创业公司市场价值分布随时间集中向终端分位数，努力值随短板增大和时间推移上升。

• 目标型模型表现出与阈值型模型高度相似的分布演化和分位数动态，但创业公司策略更趋向精确达成目标值，避免超过目标。

- 对有限玩家（$N=1000$）模拟显示经验分布和分位数良好逼近理论极限分布与分位数。

• 数值结果支持目标型模型可作为阈值型模型的有效近似。

理论贡献与模型优势 [page::2][page::10][page::20]

• 首次提出基于排名分位数的均场博弈模型，建立解析和数值两种处理框架。

- 证明目标型模型符合ε-纳什均衡性质，给出唯一解存在性。

• 结合风险投资场景，揭示动态竞争中分位数阈值设定对选拔结果与参与者行为的影响。

目标型模型 FBODE 结构 [page::6]

• 包含反馈系数$\etat,\pit$及辅助变量$\phi_t^\alpha$，描述状态均值、方差和分位数演化。

- 反馈策略结合自身状态与全局分位数，凸显均场交互特征。

• 解析性质显著提升计算效率。

阈值型模型数值迭代流程图 [page::15]

• 初始猜测分布$\mu$，计算对应分位数$q^\alpha$。

- 解决控制问题得到最优策略及状态分布$\mathcal{L}(x^*)$。

• 迭代更新分布直至收敛判定。

分位数水平对竞争激烈度的影响 [page::18][page::19]

• 随$\alpha$提升，终端分位数显著上升，竞争加剧。

- 低分位数对应目标较低，分布变化不剧烈甚至下降。

• 这表明风投设定更高选拔标准可提升获投企业平均市场表现。

实证中有限启发式样本表现与理论趋近 [page::17][page::20]

• 经验分布与理论极限分布高度一致，个体轨迹区分明确。

- 经验分位数集中分布于极限分位数附近，误差随样本量增大收敛，符合理论ε-纳什均衡误差界。

目标型模型下，状态与努力策略关系 [page::19]

• 努力与起始状态正相关，持续向目标值调整，避免超越目标。

- 与阈值型策略相比，表现出更为平滑的控制路径。

结论与实际意义 [page::20]

• 目标型提供可解析、计算高效且实际相符解，阈值型更符合实际激励结构。

- 两种模型终端分位数及分布近似一致，可互为替代。

• 该模型框架适用于分析排名竞争型动态投资与选拔问题，具推广价值。

金融科研报告详尽分析报告——《Ranking Quantilized Mean-Field Games with an Application to Early-Stage Venture Investments》

---

1. 元数据与概览

• 报告标题：《Ranking Quantilized Mean-Field Games with an Application to Early-Stage Venture Investments》

- 作者：Rinel Foguen Tchuendom, Dena Firoozi, Michèle Breton

• 机构：HEC Montréal（决策科学系）、多伦多大学（统计科学系）

- 发布时间：（未明确标注具体日期，基于引用及内容推断接近2024年）

• 研究主题：提出并分析含有分位数（quantile）作为核心耦合机制的均场博弈（Mean-Field Games, MFG）模型，定义两种分位数排名博弈的数学形式（目标基和阈值基），并将其应用于早期创业投资领域，模拟创业公司在风险投资基金支持下的动态竞赛行为。

核心论点：

• 引入一类基于样本$\alpha$-分位数的排名均场博弈，模型中代理人的表现依赖于其终端状态相对于总体$\alpha$-分位数的程度。

- 提出两种博弈模型：（1）目标基模型，代理人力图达到恰好等于该分位数的目标值；（2）阈值基模型，代理人力图终端状态至少达到该阈值。

• 全面分析目标基模型的解析解及其$\epsilon$-纳什均衡性质；阈值基模型则通过数值方法解决。

- 应用模型复现风险投资中创业公司竞争排名的实际场景，以期为风险投资组合选择提供理论依据。

主要贡献在于拓展分位数均场博弈理论，并首次提出使用此方法研究创业投资竞赛问题，展示模型在金融决策中的潜力[page::0,1,2]。

---

2. 章节深度解读

2.1 介绍与背景（Section 1）

• 介绍均场博弈的基本理论背景，解释其为建模大规模交互代理人的有效框架，强调以代表代理人对整体表现的影响进行描述。

- 指出传统MFG多基于均值而非分位数依赖，近期研究开始涉及分位数，但现有文献多限于特定动态过程，本文提出的分位数MFG模型更广泛，具备新的数学和应用问题[page::0,1]。

2.2 排名分位数均场博弈模型（Section 2）

• 描述了包含$N$个齐次代理人的有限时间竞赛框架，代理人最终状态的性能排名通过样本$\alpha$-分位数定义阈值，只有终端状态达到该阈值或以上方成功。

- 该阈值为内生产生，挑战在于它是随机且不可预知的，导致博弈耦合复杂。

• 两类具体模型：

- 目标基：终端状态应恰为$\alpha$-分位数，拥有分析可解性。
- 阈值基：终端状态至少达到该阈值，更符合实际，但解更困难，需借助数值解法。

• 目标基模型均场极限引入概率分布$\mu$的定义和$\alpha$-分位值函数$Q(\alpha,\mu)$，转为含有确定性分位值的单个代表代理人问题[page::2,3,4]。

2.3 目标基模型数学分析（Section 2.1）

• 代理人状态动态为线性扩散过程：

$$ d xt^i = (\gammat + b ut^i) dt + \sigma d wt^i $$

其中，$ut^i$指某代理的努力控制，$\gammat$为外部资金支援，$b$为效率，$wt^i$为个体随机扰动。

• 成本函数为：

$$ Ji^{[N]}(u^i,...,\alpha) = \mathbb{E}\left[\int0^T \frac{r}{2} (ut^i)^2 dt + \frac{\lambda}{2} (xT^i - qT^{\alpha,[N]})^2 \right] $$

终端成本为距离分位值的平方，模型体现努力付出有成本且代理尽量精确达成目标。

• 解决步骤：

- 无限大群体极限下代表代理问题，将经验分位数$q^{\alpha,[N]}$替换为确定分位数函数$\bar{q}^\alpha$。
- 固定分位过程$qt^\alpha$，通过随机控制求解最优策略。
- 利用分布确定性，建立自洽条件$\bar{q}t^\alpha = Q(\alpha, \mathcal{L}(xt^\star))$，形成一组前向-后向常微分方程（FBODEs），求解确定性分位数轨迹。

• 解析结果：

- 通过最大值原理和猜想法解出伴随过程$yt = \etat xt^\star + \thetat^\alpha$，$\etat,\thetat^\alpha$满足特定边值问题。
- 优化控制以$ut^\star = -\frac{b}{r} yt$形式显式给出。
- 目标分位数满足由均值和方差决定的普通微分方程，体现了代理协作对排名阈值的影响。

• 证明了策略集对有限$N$构成$\epsilon$-纳什均衡，误差随$N$递减速度约为$\mathcal{O}(1/\sqrt{N})$，误差具体依赖于分位级别$\alpha$和分布密度$p(T,\bar{q}T^\alpha)$[page::4~10]。

2.4 阈值基模型数学分析（Section 2.2）

• 代理人需终端状态不低于阈值$qT^{\alpha,[N]}$，对应终端损失函数为

$$ g(xT^i, qT^{\alpha,[N]}) = \frac{\lambda}{2}(xT^i - qT^{\alpha,[N]})^2 \mathbf{1}{\{xT^i < qT^{\alpha,[N]}\}} $$

• 控制问题变得不连续且非凸，特别是指标函数使得后向方程终条件不光滑，难以解出闭式解。

- 同样通过固定分位过程$qt^\alpha$简化问题，运用随机最大原则和FBSDEs表征最优策略，控制表达式涉及条件概率和期望，反映代理对失败概率和失落程度的反应。

• 自洽条件$qt^\alpha = Q(\alpha, \mathcal{L}(xt^\star))$，搜索固定点的求解因分位数函数的不规则性成为理论难点。

- 因此采用图1中所示迭代数值方案，先猜测分布$\mu$，计算分位值，求解控制问题，反复迭代直至收敛，完成整个均场均衡计算[page::13~15]。

2.5 早期创业投资应用（Section 3）

• 创业公司的市场价值$\{xt^i\}$被视为代理人状态，风险投资作为协调方给予确定资金流$\gammat$支持。

- 投资决策依赖于创业公司表现排名，风险投资仅进一步支持排名前$(1-\alpha)$比例的公司。

• 采用前述两种均场博弈模型模拟创业公司间资助竞争，提供策略和市场价值演变的动态解释。

- 数值实验参数固定为$T=1$，初值$\xi \sim \mathcal{N}(0,0.25)$，努力效率$b=0.5$，努力成本权重$r=0.5$，终端惩罚$\lambda=1$。

• 阈值基模型数值结果展示：

- 市场价值分布随时间向高分位数逼近，凸显顶端创业公司努力拉开差距。
- 随时间推进，分布方差减小，表现出群体努力收敛趋势。
- 策略呈现出随着离阈值越远，代理人励精图治的加码效应；超过阈值则努力趋于零。
- 高分位数$\alpha$（如0.95）带来更高的选拔门槛和更激烈竞争，低分位数动态趋于平稳。

• 有限$N=1000$时，经验分布和分位数近似极限分布和分位数，验证均场方法可行性。

- 目标基模型数值表现与阈值基相似，唯一差异为策略平滑性及超过目标时策略延续性，体现了对超额完成的罚则机制。

• 两模型选拔分位数及分布极为接近，目标基模型可作为阈值基的良好近似，且计算效率更高[page::15~20]。

---

3. 图表和图像深度解读

3.1 图1：阈值基模型数值方案流程图（page 15）

• 描述：该流程图简洁明了地呈现了迭代计算过程：初猜分布$\mu$，计算$\alpha$-分位数$q^\alpha$，解决随机控制问题得最优策略$(x^\star, u^\star)$，求最终状态分布$\mathcal{L}(x^\star)$，与初猜$\mu$比较逼近收敛。

- 意义：说明了阈值基模型因其数学难度必须通过数值迭代获得均衡分位数，确保模型的实际可操作性。

• 图示辅助理解：使抽象均场方程得到直观呈现，并为后续数值实验奠定基础。

3.2 图2：阈值基模型$\alpha=0.95$时的动态表现（page 17）

• (a) 分布时序演化：三条高斯类曲线随时间向右移动，并收敛于终端阈值，反映创业公司市场价值步步逼近并竞逐该阈值。

- (b) 分位数趋势：$\bar{q}^\alpha$显著上升，展示竞争中市场价值门槛逐步提升。

• (c) 策略立体图：越低于阈值，且时间越接近终点，努力值越大；超过阈值后努力立即减少至零。

- 含义：直观显示企业保持临界努力避免失败，且竞争动力随临近终点递增。

3.3 图3：不同$\alpha$下分位数时序变化（page 18）

• 三维曲面图：显示分位值$\bar{q}^\alpha$随$\alpha$和时间增加，表明高分位水平对应更高的竞争门槛和更明显的市场价值提升。

- 洞察：定量反映设置更高选拔比例会推高整体表现标准，优化风险投资组合品质。

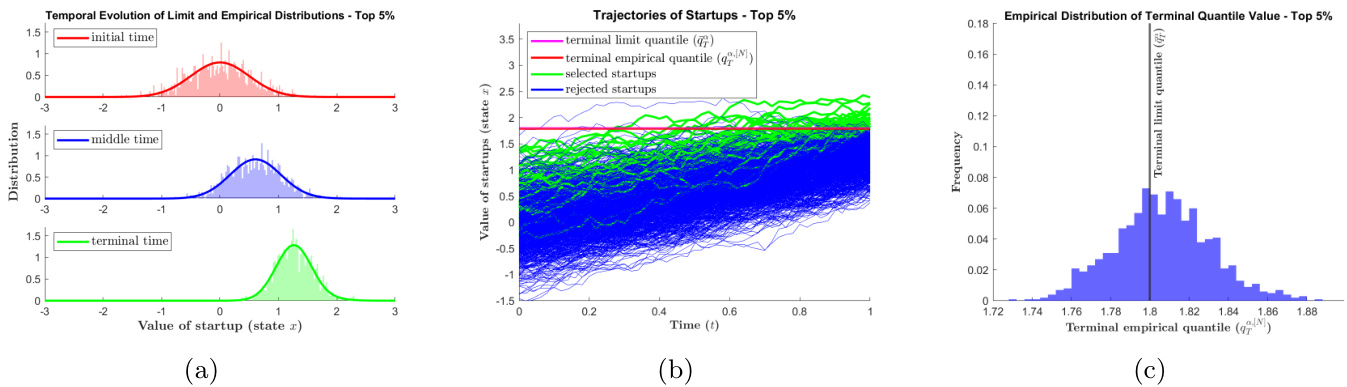
3.4 图4：有限$N=1000$个创业公司阈值基模型模拟（page 18）

• (a) 分布曲线与柱状拟合：极限分布曲线良好拟合真实模拟数据直方图，验证均场极限的现实适用性。

- (b) 轨迹图：清晰区分绿色（成功）与蓝色（失败）创业公司，展示在竞争中动态调整提出努力的过程。

• (c) 经验分位数直方图：集中分布在极限分位数附近，样本量越大，经验分位数对极限分位数的估计越精准，呼应理论纳什误差结果。

3.5 图5-7：目标基模型在不同场景下对应图示（page 19-20）

• 理论和数值表现均与阈值基类似，但多个图表显示目标基策略更平滑且对超额完成有惩罚，导致市场价值分布更加集中。

- 经验分位数与极限分位数吻合度更高，说明其作为阈值基的近似具备良好数学和数值稳定性。

---

4. 估值分析

本报告核心涉及的数学工具与估值体系并非直接金融资产估值，而是对创业公司市场价值演变和竞争策略形成的动态系统建模：

• 利用均场博弈（MFG）理论将多人动态竞赛转化为无限代理极限下单代理问题，通过控制理论和随机微分方程描述投资成果（市场价值）和策略演化。

- 适用的估值指标为模型稳定时的$\alpha$-分位数阈值$\bar{q}t^\alpha$，作为选拔创业公司的标准或风险投资策略目标。

• 两种模型中：

- 目标基模型对应控制问题中存在解析式反馈控制策略，终端状态通过均值和方差动态调整得到，便于计算衡量投资组合的价值演变。
- 阈值基模型通过数值迭代确定最优控制及分布，计算精细但无闭式表达。

• 报告中无现金流折现或传统资产估值因子，估值分析更多侧重策略合理性及其对创业公司和风险投资基金风险收益关系的解释。

---

5. 风险因素评估

报告主要风险点体现在建模及实用层面：

• 模型假设风险：

- 同质代理假设简化现实多样化创业公司，但可能忽略了异质性对竞争结果的影响。
- 使用Wiener过程模拟市场价值随机性简单，未涵盖跳跃风险等异常事件。

• 数学难题：

- 阈值基模型存在理论上未解的固定点唯一性和稳定性问题，影响均衡策略的确定性和可靠性。

• 数值近似误差：

- 数值解法依赖迭代收敛和样本容量，有限$N$下存在估计误差和离散影响。

• 实际应用局限：

- 创业公司市场价值受多因素叠加影响，模型中的策略控制变量未必全面。
- 初创投资领域非纯博弈性，还涉及外部环境、行业趋势、监管政策变动等实际不可控风险。

报告并未明确提出缓解上述风险的具体方案，预留进一步数学研究与扩展考察空间[page::13,14,20]。

---

6. 批判性视角与细微差别

• 假设限制：

- 报告假设市场价值动态和努力效率为线性关系，可能弱化非线性创新机会和规模效应。
- 分布和策略的正态性假设在创业领域可能不准确，因为创业表现往往截尾严重，存在重尾分布。

• 模型差异解释：

- 目标基模型封闭解优势明显，但其对超额表现施加惩罚，现实中创业公司可能追求超额回报，此假设略显理想化。

• 理论开放性：

- 阈值基模型的数学未定性使得其均衡策略和纳什误差表现未完全确定，需后续研究完善。

• 实验结果之间的细微差别：

- 虽两模型输出接近，但付出的努力策略存在差异：目标基持续调整，而阈值基努力中断，更贴合经济直觉。

• 文献回顾局限：

- 报告对创业投资的量化文献提及有限，建议未来更密切结合实际融资数据和市场表现。

整体来看，作者客观呈现模型优势同时坦诚存在的学术与实务难题，为后续科研发展奠定基础[page::2,14,20]。

---

7. 结论性综合

本文通过引入排名分位数概念，丰富了均场博弈理论，区分了目标基和阈值基两种分位数排名博弈：

• 目标基模型具有强大数学解析性质，提出的FBODE系统确保了均衡策略的存在性、唯一性和纳什近似性质，便于快速计算。代理人努力控制具体且光滑，贴近期望达到确切目标的创业行为。

- 阈值基模型更直观符合实际竞赛规则（达到或超过门槛即可），但数学复杂度高且均衡策略无解析解，需数值迭代，策略呈现截断性质，表现更具现实感。

• 两模型在创业投资应用中均表现出相似的市场价值分布和分位数阈值，目标基模型可作为阈值基的有效近似，大幅提升计算效率且维持理论精度。

- 数值实验全面展示了不同分位水平下创业公司市场价值的时序演进，揭示了竞赛激烈度和策略调整规律，对风险投资决策具有重要启发。

• 论文绘制的迭代算法框架及随机控制模型为相关复杂金融问题建模和求解提供了新思路。

- 研究开辟了基于排名分位数的均场博弈在金融投资领域的新应用路径，强调必要的理论与数值方法创新以促成实际落地。

总之，本报告从数学理论到数值实现，再到创业投资的具体应用，构筑起一个系统且具有创新性和实用潜力的分位数均场博弈研究框架，其贡献和深度对金融工程和风险投资管理学科均有较大价值[page::0~21]。

---

附：关键公式与符号说明

| 符号 | 说明 |
|-------|--------|
| $xt^i$ | 代理$i$在时间$t$的状态（创业公司市场价值） |
| $ut^i$ | 代理$i$在时间$t$的控制（努力水平） |
| $\gammat$ | 协调者（风险投资）提供的确定性支援资金 |
| $b$ | 努力效率系数 |
| $\sigma$ | 随机波动率 |
| $qT^{\alpha,[N]}$ | $N$代理终端状态的样本$\alpha$-分位数（排名阈值） |
| $\bar{q}t^{\alpha}$ | 极限分位数，$N \to \infty$时的确定性阈值 |
| $Ji$ | 代理$i$的成本函数，包含努力成本与终端目标偏差成本 |
| $\epsilon$-纳什均衡 | 在有限玩家游戏中，策略组近似纳什均衡，偏差可容忍小量$\epsilon$ |

---

图片示例

图2示例：阈值模型下创业公司竞争情形逐渐演化



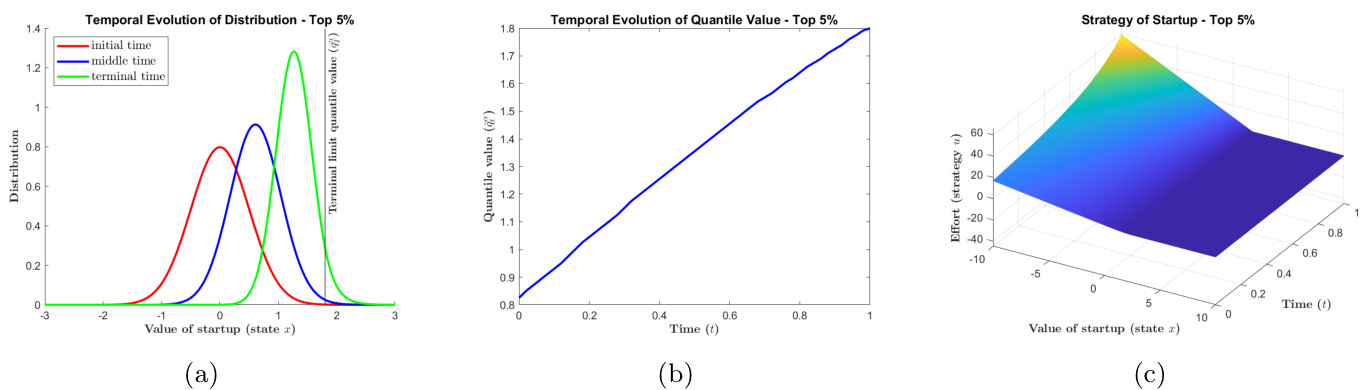
图4示例：有限样本创业公司市场价值和分位数动态



---

（全文基于报告原文第0至21页内容综合解读）

报告