• 研究基于S&P500 2019-2024年股票数据，构建以股票为节点、收益率相关矩阵阈值化生成的金融市场网络。网络呈现典型无标度特征，存在72个Louvain社区，部分社区与传统行业划分不完全一致，体现市场深层结构[page::1][page::2][page::3]

• 网络节点的度、特征向量中心性、聚类系数等指标揭示关键影响股票及其潜在风险传染性，聚类高的网络结构提升系统稳健性，有助于优化投资组合的风险控制[page::4]
• 应用随机矩阵理论（MP分布）将收益率关联矩阵特征值分解为市场模式和噪声模式，其中最大12个特征值对应集体市场模式，由具高特征向量中心性和PageRank的关键节点驱动。

- 12个关键市场模式股票主要来自金融、工业、信息技术三大行业。
- 以这12只股票构建市场模式相关矩阵，其他特征值构成噪声相关矩阵[page::5][page::6]

• 通过引入基于几何布朗运动（GBM）的相关随机游走模型，实现对市场模式和噪声模式收益率相关矩阵的模拟。模型中相关性由Louvain社区标签及网络聚类系数决定，同时引入个别市场模式主导的相关性权重。

- 使用Wasserstein距离优化模拟权重，市场模式权重约74%，噪声部分绝大多数由纯GBM解释，支持噪声中仍存在低强度相关[page::7][page::8]

• 模拟结果与真实数据在收益率相关矩阵的分布及特征值谱上高度一致，证明简单GBM结合网络信息即可有效重现复杂金融市场相关结构。

相关权重结果总结：
| 权重类型 | 比例 | 含义 |
|---------|-----|------|
| $wL$（社区相关） | 0.26-0.20 | 体现集群内的相关性影响 |
| $wM$（市场相关） | 0.62-0.74 | 体现主要市场主导股票相关性 |
| $w_N$（噪声） | 0.03-0.18 | 主要为无相关性噪声成分[page::10]

• 利用模拟市场模式GBM生成的协方差矩阵，结合Markowitz均值-方差优化模型，构造基于非历史真实数据的投资组合。

- 研究不同再平衡周期对组合表现影响，发现以约84天（252/3日）为最佳，模拟模型在中短期表现优于基准历史模型。
- 模拟模型比基准模型在部分时间段累计收益最高提升达50%，证明去噪后的网络驱动相关矩阵更适合短期组合管理[page::11]

• 结论强调结合复杂网络方法识别集体市场模式及关键信股票，有助于揭示股票间深层关联，提升建模精度与投资组合回报。未来研究可拓展至更复杂时变波动模型如Heston及GARCH模型以模拟市场动态[page::12][page::13]

报告详尽分析：从复杂网络分析推断金融股票收益率的相关性

---

1. 元数据与报告概览

标题：Inferring financial stock returns correlation from complex network analysis
作者：Ixandra Achitouv
机构：法国国家科学研究中心（CNRS），复杂系统研究所ISC-PIF
时间：文中数据截至2024年1月，具体发布日期未知
主题：运用复杂网络分析与随机矩阵理论（Random Matrix Theory, RMT）结合模拟几何布朗运动（GBM）模型，解析股票收益率相关性结构，探讨其对投资组合优化的应用。

报告核心论点：

• 股票收益率相关矩阵中的“市场模式”和“噪声模式”可通过RMT区分，但对集体现象的单纯RMT解释较为有限。

- 结合复杂网络分析方法，利用股票之间的网络特性（如节点的度、中心性、聚类系数及Louvain社区检测）能更深入理解相关矩阵中的集体现象。

• 基于此网络特性构建的相关模型能有效模拟真实数据的相关性结构，且能通过模拟市场随机游走改进投资组合的构建，提升短期投资回报率约50%。

作者强调，将网络科学与传统金融时间序列方法结合，为理解和应用股票相关性提供新视角，特别是在投资组合优化方面有明显实用价值 [page::0,1,6,11].

---

2. 逐节深度解读

2.1 摘要与引言

报告开篇介绍了利用随机矩阵理论（RMT）区分金融资产收益相关矩阵中的信号与噪声的理论基础，特别突出最大特征值（市场模式）和其他特征值含义的难以直观解释。作者提出用复杂网络理论分析集体现象，结合相关矩阵与网络构造理解股票间相互影响的机制，指向系统性风险评估和投资组合优化应用，体现跨学科研究的创新性[page::0].

2.2 网络构建（章节2）

数据集与过滤：

• 选取S&P 500指数成分股，剔除区间内缺失的股票，最终485只股票，时间跨度从2019年1月1日至2024年1月1日，共1258个交易日。

- 11个行业板块进行类别标注，方便后续对行业聚类和区分的分析[page::1].

相关矩阵及邻接矩阵构造：

• 计算股票对数收益率的相关系数矩阵。

- 采用过滤阈值方法，将相关系数大于阈值（$\rhoc=0.9$）的边视为存在连接，否则置零，得出加权邻接矩阵。此高阈值导致网络呈幂律分布形态，形成典型“无标度网络”，即少数核心节点连接众多节点，大部分节点连接较少[page::1].

2.3 网络分析（章节2.3-2.4）

定义并计算：

• 节点度（Degree）

- 特征向量中心性（Eigenvector Centrality）：反映节点对整体网络影响力。高中心性节点连接许多重要节点，具系统性风险放大效应。

• 局部聚类系数（Clustering coefficient）：节点邻居间连接密度，用于衡量局部连接冗余和网络的抗损伤能力。

利用ForceAtlas2算法作网络可视化，节点大小依据度大小，颜色对应行业。观察到部分行业如公用事业、能源、信息技术、医疗保健等形成较明显的簇状聚类，而金融、工业品、消费品等行业较为分散。使用Louvain算法识别出72个社区，其中15个社区含多只股票，显示网络结构与传统行业分类有所不同。
网络底部图表表明度分布呈无标度幂律分布，特征向量中心性分布右偏，聚类系数以0.4附近为均值且带有尾部分布。高聚类系数通常对应网络鲁棒性，可以为投资组合设计提供启示。报告强调以网络中心性替代传统标准差作为风险度量指标对提升投资组合效果的潜力[page::2,3,4].

2.4 RMT与股票收益率相关矩阵的模型构建（章节3）

经典RMT分析：

• 运用马尔琴科-帕斯图分布（Marchenko–Pastur，MP分布）描述理论上随机相关矩阵的特征值分布，用以判别数据中的“噪声”与“信号”。

- 实际数据中最大特征值显著超出MP分布上限，对应市场模式，反映整个市场的集体运动。

• MP分布匹配部分特征值的分布，但实验数据的连续谱与MP理想曲线存在较大差异，表明噪声中存在一定相关结构（例如波动率相关性），引出区分噪声内部结构的必要性[page::4].

引入相关几何布朗运动（GBM）模拟股票价格：

• 基于历史数据计算个股初始价格$S0$，漂移$\mu$，波动率$\sigma$。

- 相关结构通过引入两个参数：相关系数$c{eff}$和随机游走的固定种子$si$，生成部分共享随机成分的相关随机游走。

• 通过调节$c{eff}$和种子实现股票间自定义相关结构的模拟，从而捕捉“市场模式”和“噪声模式”的相关性特征[page::5,6].

“市场模式”提取与模拟：

• 选取排名前3%且PageRank最高的股票节点计为最具影响力的股票，数量$n{market}=12$，分别来自金融、工业、信息技术三大行业。

- 这12只股票对应的特征值共占有很大权重，选定为市场模式，其他归为“噪声模式”。

• 对市场模式相关矩阵进行特征分解，恢复仅含市场模式信息的相关矩阵并归一化形成$C^{Market}$。

- 模拟时引入两种相关机制：（1）基于Louvain社区的相关性，种子对应社区编号，权重为节点聚类系数；（2）基于市场模式影响，种子固定，权重为对应节点与市场模式股票最大相关性。

• 以加权组合方式生成模拟市场随机游走$St$，参数通过最小化 Wasserstein距离（衡量分布差异）调优[page::6,7].

“噪声模式”提取与模拟：

• 对剩余特征值对应空间提取噪声相关矩阵，定义纯GBM（无相关，$c{eff}=0$）与社区相关GBM的加权组合生成模拟噪声随机游走。

- 权重同样通过Wasserstein距离优化确定[page::7,8].

生成总相关矩阵模型：

• 最终将市场模式、噪声模式和社区结构的随机游走按权重组合，生成完整模拟相关矩阵$C^{GBM}$，实现对整体相关性结构的拟合。

- 实验证明使用社区聚类优于单纯用行业分类，更好体现市场相关性特征[page::8].

---

3. 重要图表解读

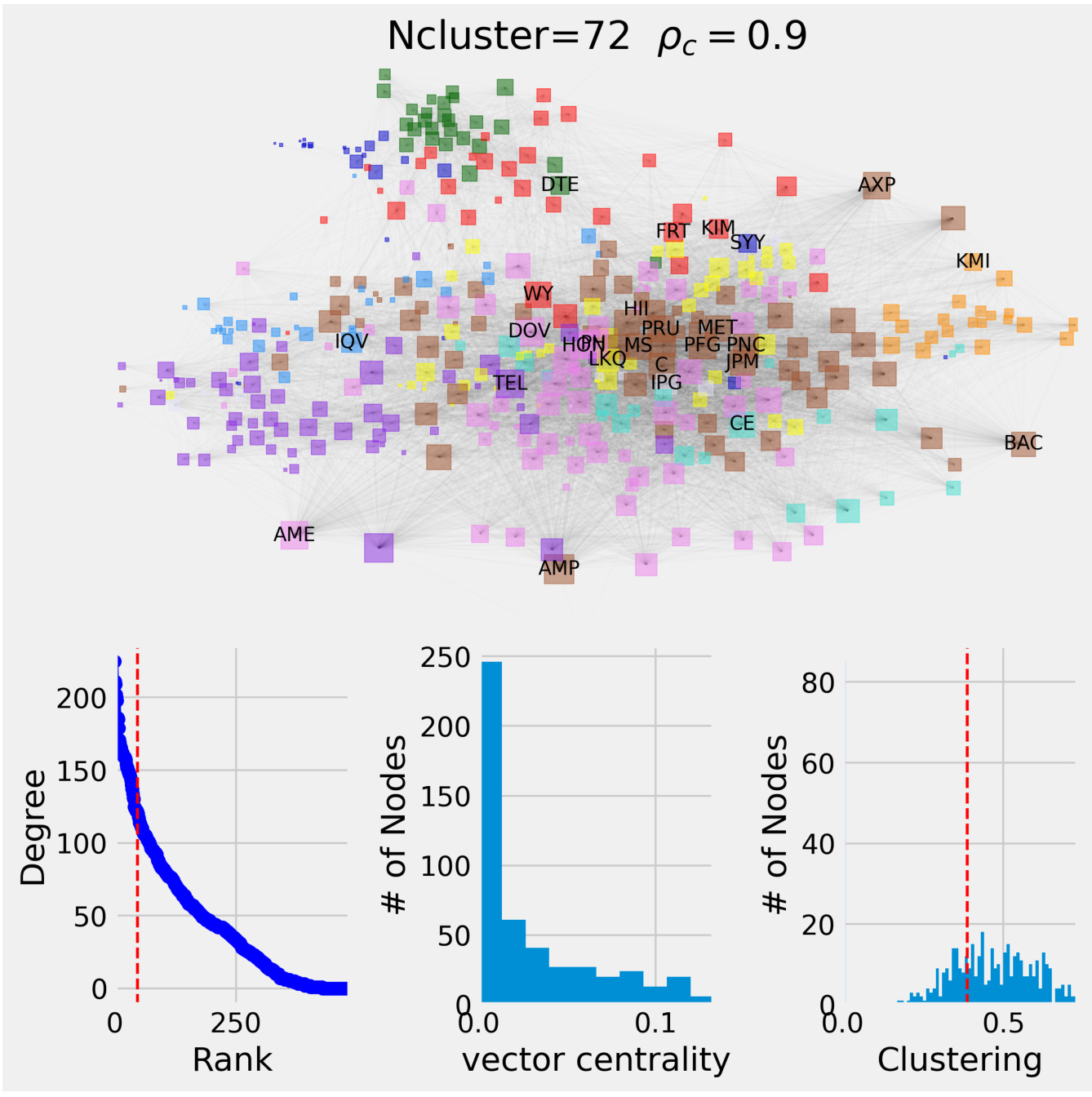
3.1 图1（页面2）股票网络结构与分布特征图

• 内容描述：

顶部为股票网络图，不同颜色表示11个行业板块，节点大小对应度。底部三个直方图依次为：节点度分布、特征向量中心性分布及聚类系数分布。红色竖线为对应均值。

• 数据趋势与解读：

度分布呈明显幂律下降，体现无标度网络特性，即少数股票扮演“枢纽”角色，是系统风险放大的关键点。
特征向量中心性分布高度右偏，表明部分节点极具市场影响力。
聚类系数分布显示较高的局部网络紧密性，意味着股票间局部关联强，形成社区。
不同行业聚集现象明显，如公用事业及能源板块集群较紧密，而金融、消费品较散。

• 文本联系：

网络结构支持股票间存在明显的社区效应和市场集体运动，且高中心性节点可能是市场波动的“引爆点”，值得关注投资组合风险[page::2,3,4].

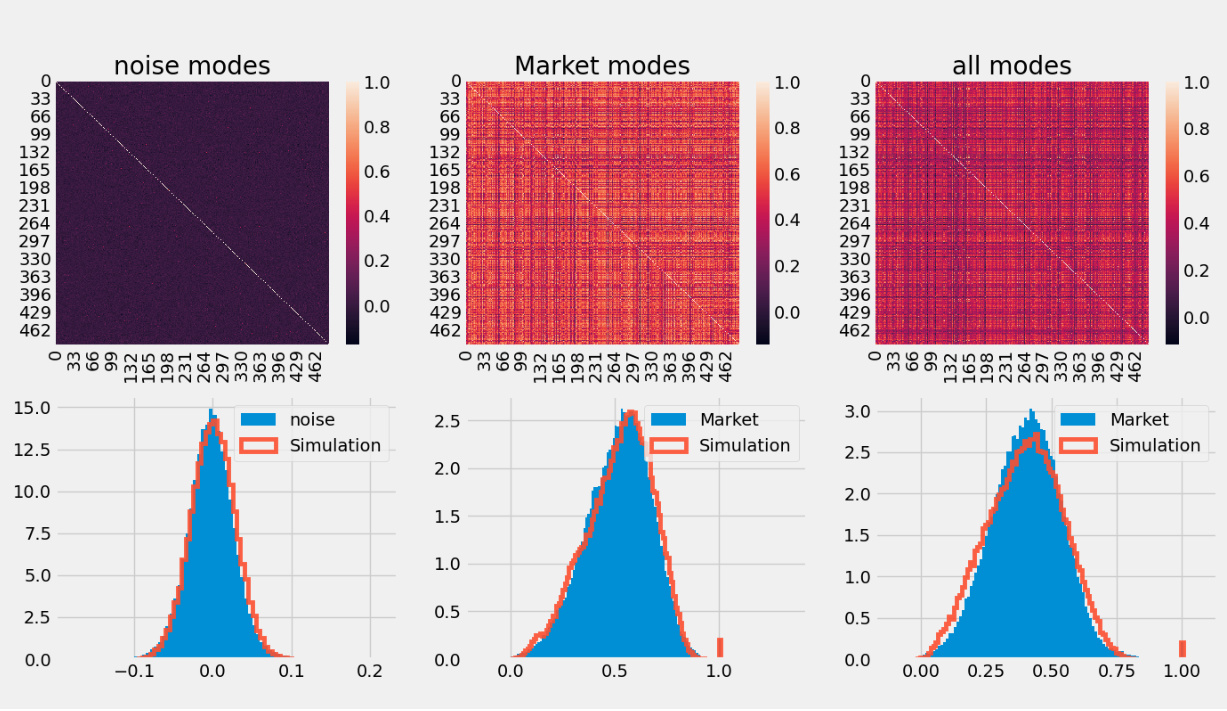
3.2 图2（页面9）数据与模拟的相关矩阵和相关值分布

• 内容描述：

上半部分展示分解后的三种相关矩阵热图：噪声模式、市场模式、全相关模式。
下半部分为对应数据（蓝色）与模型（红色）相关系数分布的直方图对比。

• 数据趋势与解读：

噪声模式相关系数近似服从以0为中心的正态分布，标准差约0.05，模拟与数据高度吻合。
市场模式相关系数明显偏离0，均值约0.52，对应强烈的市场集体现象，模型能较好复制该特征。
总相关矩阵的分布表现介于两者之间，模拟重建的相关结构贴合真实数据。

• 文本联系：

模拟GBM方法能够以简单模型捕捉相关矩阵的主要统计特征，包括噪声与信号分布，支撑后续基于该模型的投资组合构建[page::8,9,10].

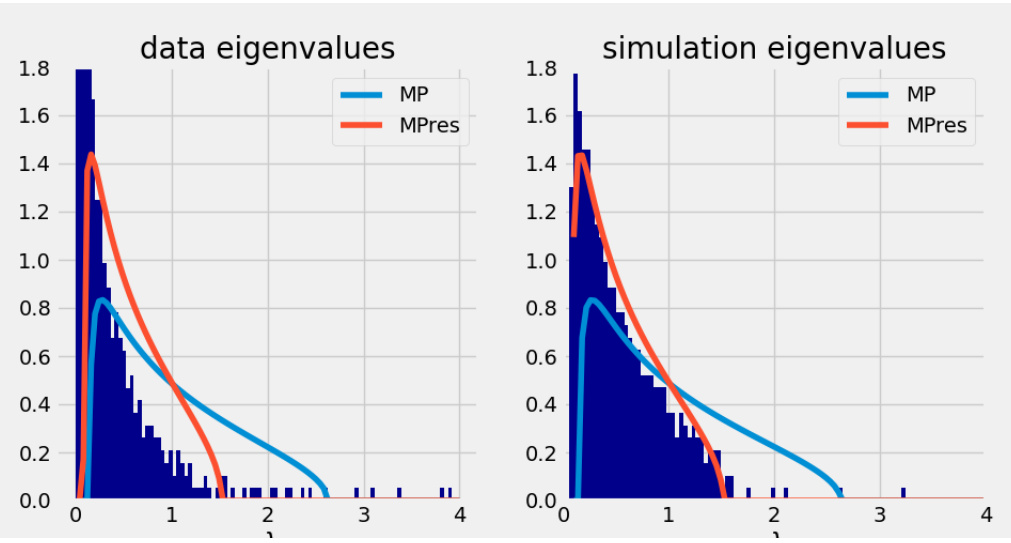
3.3 图3（页面9）特征值分布与MP分布对比

• 内容描述：

左右两图分别展示真实数据和模拟数据的特征值分布直方图，叠加了未经缩放和经过调整的MP理论曲线。

• 数据趋势与解读：

最大特征值均显著超出MP理论上限（约203），对应市场模式，模拟复制表现良好。
连续谱内部特征值分布不完全符合MP曲线，表现为较低的“凹度”，表明存在非纯随机结构，暗示简单GBM未捕获波动率相关性。
模型在整体趋势和极端特征值预测上具有较好拟合效果，这验证了其有效性。

• 文本联系：

证实了复杂网络模型引入的相关性对于解释实证特征值分布不可或缺，也说明简单模型虽然有局限，但能突出主导相关行为[page::9,10].

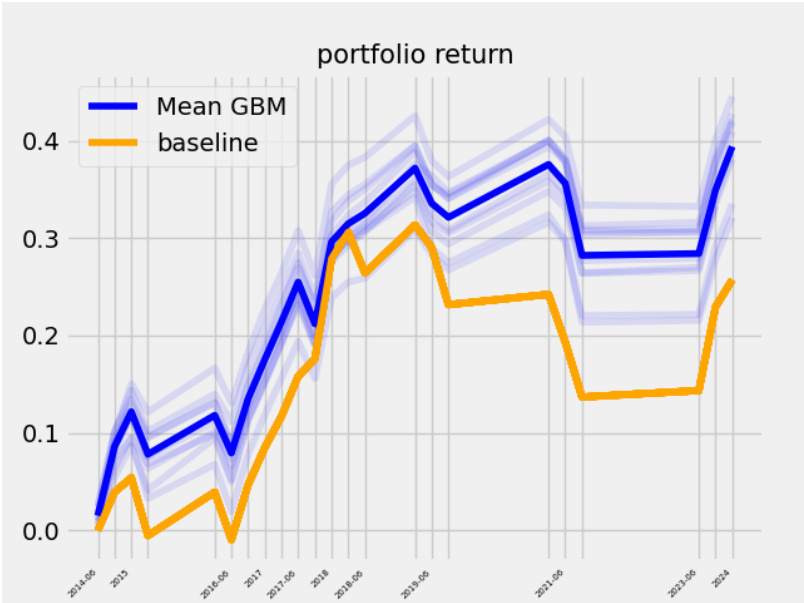
3.4 图4（页面12）基于模拟市场GBM与历史数据的投资组合收益比较

• 内容描述：

展示不同时间段内基于传统历史均值-方差模型（橙色曲线）和模拟市场相关随机游走（蓝色曲线）的累计最优投资组合收益。

• 数据趋势与解读：

模拟方法在大多数短期重新平衡周期（≤84天）表现优于传统模型，累计收益最高时可提升至50%。
长周期下传统模型表现更优，原因在于GBM模拟期望收益与真实未来收益差距增大。
曲线中蓝色带显示10次模拟的波动范围，表明结果稳健且波动可控。

• 文本联系：

实证证明基于市场模式和网络特性的模拟GBM走势提供更有效的风险调整投资组合策略，尤其适合中短期投资规划，验证了复杂网络在资产管理中的实际价值[page::11,12].



---

4. 估值分析

报告不涉及传统的市场估值方法如DCF或P/E估值，而是聚焦于金融资产相关关系的数学模型构建和投资组合优化中的风险-收益结构。其对估值的贡献表现在：

• 通过区分市场模式和噪声对股票相关性结构的解析，帮助改进资产协同风险的评估。

- 利用模拟相关性矩阵替代历史相关矩阵，以更准确捕捉潜在的市场风险，并优化资产权重分配。

• 投资组合优化基于Markowitz平均方差框架，但输入改用模拟GBM输出的协方差矩阵，体现一种创新的估值方法论在投资组合构建中的应用。

具体的投资组合权重通过二次规划问题求解，考虑预测收益和协方差矩阵，采用最大Sharpe比率作为目标函数，权重下限约束保证持仓多样性[page::10,11].

---

5. 风险因素评估

报告隐含识别和间接评估了多个风险因素：

• 系统性风险： 通过网络分析确定的高中心性节点，因其连接广泛，导致市场冲击易于传播和放大，增强系统风险传导。

- 模型风险： 基于GBM的假设具有局限，如固定波动率和漂移，忽略波动率集群和非正态收益分布，长期预测稳定性受限。

• 数据风险： 取样窗口及股票数据完整性决定模拟精度，部分数据缺失处理可能影响结果。

- 重新平衡频率风险： 投资组合表现对重新平衡周期极其敏感，过短或过长周期均可能降低优化效果。

• 噪声解释风险： 噪声模式并非完全随机，可能含有波动率相关等结构性信息，简单处理可能误判真实风险。

缓解措施方面，作者通过优化权重$wL, wM, wN$并使模型在分布拟合上最小化Wasserstein距离，大幅提高模型匹配度，间接降低模型偏差和噪声误判风险。但未见风险发生概率明确量化[page::4,8,10].

---

6. 审慎视角与细微差别

• 模型简化假设限制： 采用经典GBM模型无法捕捉现实市场中的波动率波动、跳跃过程和极端尾部风险，模型虽然能还原部分数据统计特征，但深层风险隐患可能被忽视。

- 社区划分与行业分类不完全吻合： 报告指出基于复杂网络的社区结构与传统行业分类存在明显差异，显示市场行为超越单一行业划分，这对行业投资策略提出挑战。

• Louvain社区参数敏感性： 社区划分对算法参数敏感，稍有调整可能影响划分结果，进而影响模拟权重和投资组合优化的可靠性。

- 权重统一假设： 模型中模拟相关游走的权重（如$wL, wM, wN$）对所有股票均相同，这在现实中可能过于简化，不同股票受市场影响和社区影响程度差异较大。

• 时间窗口选择及滚动推断： 不同时间尺度的表现差异显著，最优重平衡周期为84天，对投资策略稳定性影响大。

- 文中未深入探讨投资组合回测的交易成本和市场摩擦，实际应用时需考虑。

总体来看，报告基于实证与模拟取得有力结果，但结果对参数选取和模型简化依赖较强，未来增强模型复杂度及风险识别能力有助提升结果稳健性[page::4,6,11,12].

---

7. 结论性综合

本报告通过结合随机矩阵理论与复杂网络科学方法，解析了美国标普500股票收益率的相关结构，取得以下关键发现：

• 股票收益相关矩阵可分解为代表市场集体行为的“市场模式”与接近噪声的“噪声模式”，明显区分了信号与噪声结构。

- 基于股票间复杂网络属性（度、特征向量中心性、聚类系数、Louvain社区划分）构建的相关性模拟，能够较好重现真实数据的统计特征，包括相关系数分布、特征值谱分布和网络结构。

• 通过用定制的相关GBM模型模拟股票价格路径，构造出的投资组合优于传统历史均值-方差模型，在短至中期频率重新平衡条件下能提升最高达50%的累计收益率，显示网络驱动的相关结构提取具备实证投资价值。

- 相关性中的复杂社区结构比传统行业划分更好捕捉市场动态，显示系统性风险和集体现象的多层次特点。

• 模型虽然依赖GBM简化假设，未涵盖波动率聚类和跳跃等现实特征，但已证明基础模型结合复杂网络分析可显著提升对金融市场内在相关性的理解和投资策略设计。

- 作者指出未来可进一步采用更复杂的随机过程模型（如Heston或GARCH模型）改进模拟效果，提升预测能力和风险评估[page::0-4,6-10,11-13].

综上，Ixandra Achitouv的工作有效将复杂网络科学引入金融关联结构分析领域，不仅扩展了对市场集体现象的理解，也为投资组合优化提供了创新方法，推动了金融市场系统风险和资产管理的理论与实践发展。

---

以上分析紧密结合报告内容及页面标注，力求全面、细致解释所有重要论点、数据与图表，具备充分的技术深度和金融专业性。

报告