• 研究背景与问题定义 [page::0][page::1]

- 合并旨在产生协同效应，即合并后企业股权价值的正向变化。
- 经典LG-Y模型确定了股票换股比例的议价区间（BR），基于股权价值的确定性比较。

• LG-Y模型的确定性框架及扩展 [page::1][page::2]

- 交换比率 $r$ 的界定基于公司股权价值和股票数量。
- 存在仅基于股权价值的议价区间 $B\mathcal{R}{\mu}(\mu{M})=[\underline{r}\mu, \overline{r}\mu]$，协同效应越大，区间越宽。

• 风险维度的引入及随机扩展 [page::3][page::4]

- 将股价视为随机变量，定义风险测度 $\varphii$，引入风险调整后的绩效指标 $\lambdai = pi/\varphii$。
- 针对风险定义相应的议价区间 $B\mathcal{R}\rho(\rhoM)=[\underline{r}\rho, \overline{r}\rho]$，需满足风险优势条件。

• 结合预期价值和风险的双维议价及一致区间 [page::4]

- 定义了对股东双方均增加预期财富且减少整体风险的交换比率一致区间 $\mathcal{C R}A$ 和 $\mathcal{C R}B$。
- 该条件依托协同效应的大小 $s$ 与风险降低幅度 $v$，界定股东接受合并的必要阈值。

• Kulpa的区间图示法及二维解读 [page::5][page::6]

- 利用Kulpa方法将区间映射为二维平面上的点，交换比区间转化为中点与半径坐标$(x,y)$。
- 预期财富区间和风险区间分别对应两条超曲线 $\gamma(\muM)$ 和 $\delta(\rhoM)$，定义可接受交换比的轨迹。

• 不同情形的图示与区域划分 [page::7][page::11]

- 论文详细划分4种主要情况（两致区域和两一致区域）以解析股东对交换比率的接受区间。

• 图示区间为空的情况及其经济含义 [page::13]

- 若协同效应或风险收益不足，交换比率一致区间为空，合并难达成共识。

• 数学推导与超曲线性质 [page::14][page::15]

- 交换比率区间对应超曲线的具体代数方程和几何特征，阐释图示数学原理。

• 结论 [page::12]

- 引入风险度量后，股东对交换比率的态度出现正交互性，资金价值提升同时伴随风险加剧。
- Kulpa图示方法便于理解双维风险与价值影响下的谈判空间。
- 本框架为合并股权交换比率的风险调整分析提供理论基础，未来可结合期望效用等方法拓展。[page::0][page::3][page::4][page::6][page::12]

详细分析报告：Displaying risk in mergers: a diagrammatic approach for exchange ratio determination

---

一、元数据与报告概览

• 报告标题：《Displaying risk in mergers: a diagrammatic approach for exchange ratio determination》

- 作者：Alessandra Mainini, Enrico Moretto (通讯作者), Daniela Visetti

• 机构：Università Cattolica del Sacro Cuore (意大利皮亚琴察), Università di Milano-Bicocca (意大利米兰)

- 时间：文章内容没有明确显示具体发表时间，但参考文献近至2023年，且致谢中提及2022年的事件，推测为2022年至2023年间发表。

• 主题领域：并购交易中交换比率的风险调整确定，特别在股票换股协议下，基于风险衡量的交换比率讨价还价区域（Bargaining Region，BR）确定。

- 报告核心论点：
- 在考虑不确定性和风险的环境中，为并购中的股票换股制定交换比率设定上下界以保障双方股东利益。
- 利用Kulpa提出的区间图示法，将二维区间映射为平面点，解决双维（价值和风险）讨价还价区间难以直观展示的问题。
- 该方法将传统确定性模型推广至随机情境，引入风险量度构建更现实的讨价还价区域。
- 并明确了有风险调整条件下，双方股东对接受交换比率的期望和风险承受产生不同影响，形成复杂的讨价还价局面。

• 发表目标：为学术界提供在随机风险因素参与并购交换比率确定的新理论框架，补充传统确定性模型的不足，同时利用图示法提升解析和理解能力。

---

二、逐节深度解读

2.1 报告引言与文献回顾（第0-1页）

• 报告首先概述了并购作为研究主题的重要性与已有丰富文献（King et al., Risberg et al.等），并提出并购的核心动机是“协同效应”（synergy），即合并后公司的股权价值行为优于合并前两家公司各自股权的简单加总。

- 明确聚焦于股票换股协议中“交换比率”(exchange ratio, ER) 的确定问题，即合并后目标公司股东用多少母公司股票换取自己公司股票，换股比例的合理确定直接关系到各方股东价值收益。

• 文献回顾中指出，传统LG-Y模型（Larson & Gonedes，Yagil）在确定性框架下，给出了讨价还价区域(BR)的明确区间，但未涉及风险和随机环境。

- 近期部分研究（Moretto & Rossi等）引入风险调整，但未给出讨价还价区间而只给出唯一风险调整的ER。

• 本文立足于股票换股协议，目标是扩展LG-Y框架至随机风险环境，明确两个集团股东的合理ER上下界，进而定义更严谨的讨价还价区域。

- 引入Kulpa提出的区间图示法，将二维风险和期望价值约束的复杂区间映射到二维平面点，解决传统纯数值区间难以直观展示问题。

• 结构布局简单明了：第二章阐述理论框架，第三章展示Kulpa图示法应用及金融意义，第四章总结[page::0,1]

2.2 确定性基准模型：LG-Y 设定（第1-2页）

• 定义三家公司的股价、股票数量、股权价值：$pi, Ni, \mui = pi \cdot Ni$，$i=A,B,M$。

- 合并股票数量关系：$NM = NA + r NB$，其中$r$是交换比率。

• 合并带来正协同时满足：$\muM \geq \muA + \muB$。

- 核心关键比率$r = pB / pA$ ，衡量B相对A股票价值。

• 通过股价不减原则，对双方股东设置价值收益保持条件，推导出交换比率上下界：

- 股东A接受的最大ER：
$$
r \leq r \frac{\muM - \muA}{\muB} = \overline{r}\mu(\muM)
$$
- 股东B接受的最小ER：
$$
r \geq r \frac{\muA}{\muM - \muB} = \underline{r}\mu(\muM)
$$

• 结合条件$\muM \geq \muA + \muB$，两个边界合法且满足$\underline{r}\mu \leq \overline{r}\mu$，定义价值得到改善的讨价还价区域$B\mathcal{R}\mu(\muM)=[\underline{r}\mu, \overline{r}\mu]$。

- 若无协同效应$\muM = \muA + \muB$，讨价还价区间退化为单点$r$。

• 通过图1（见图）可视化该讨价还价区间，明示不同联动价值条件下交换比率区间变化。

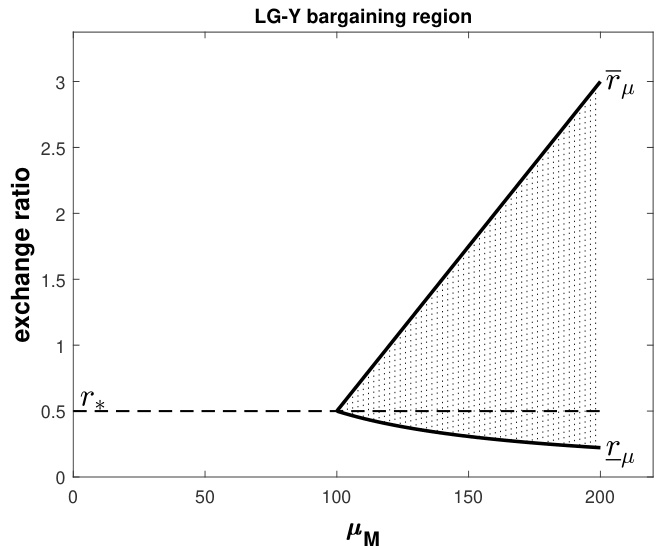
• 该段明确LG-Y模型的局限，仅以期望股权价值为目标，未考虑风险因素[page::1,2]

2.3 风险度量引入及随机环境扩展（第2-4页）

• 引入价格随机变量$\tilde{p}i$，不依赖特定分布，关注期望$mi$及同质风险度量$\varphii$，符合Artzner等人定义的相干风险度量。

- 设$mi = pi$简化记号，与确定性模型期望对应。

• 定义股权风险总量$\rhoi = \varphii \cdot Ni$。

- 提出对应的风险交换比率比值
$$
r{} = \frac{\varphiB}{\varphiA}
$$

• 风险调整后股东A风险减少条件得到对应的ER下界：

$$
r \geq r{} \frac{\rhoM - \rhoA}{\rhoB} = \underline{r}\rho(\rhoM)
$$
条件要求$\rhoM > \rhoA$保证正值。

• 风险调整后股东B风险减少条件推出ER上界：

$$
r \leq r{} \frac{\rhoA}{\rhoM - \rhoB} = \overline{r}\rho(\rhoM)
$$
条件$\rhoM > \rhoB$保证正值。

• 随机风险调整的讨价还价区间定义为

$$
B\mathcal{R}\rho(\rhoM) = [\underline{r}\rho(\rhoM), \overline{r}\rho(\rhoM)]
$$
存在当$\max\{\rhoA, \rhoB\} < \rhoM \leq \rhoA + \rhoB$。

• 关键发现：价值交换比率上下界和风险交换比率上下界分别给出，对于股东A，价值维度上希望$r$尽可能小以最大化期望收益，但风险维度$r$需要足够大以降低单位股票风险，二者产生权衡，反之股东B对$r$的偏好呈相反趋势。

- 设定两个一致性区间$\mathcal{CR}A$和$\mathcal{CR}B$，分别反映在价值与风险均能改善的条件下每方认可的ER范围[page::2,3,4]

2.4 协同效应与风险减小对一致性区域影响（第4页）

• 以$ s \geq 0$表示预期协同，$v \geq 0$为风险减小，定义$\muM = \muA + \muB + s$，$\rhoM = \rhoA + \rhoB - v$。

- 阐述无协同无风险改善时，股东A、B接受合并的条件直接依赖两家公司的风险调整绩效指标$\lambdai = pi / \varphii$大小关系，具体为
- 若$\lambdaB \geq \lambdaA$，股东A即使没有协同收益亦可接受合并，反之亦然。

• 指出了股东接受区间依赖协同和风险减小程度，给出了对应对冲阈值$\overline{s}A, \overline{s}B$ ，协同越大或风险减小越显著，接受的范围越宽。

- 列出了讨价还价区域重合的六种案例（详见表1，尽管表因格式问题未完整显示），其中4种为非空区间。

• 以降低维度的思路，将讨价还价区域的$\muM, \rhoM$的变化映射至二维坐标平面，用以简单明了表示交集区间[page::4,5]

---

三、图表深度解读

图1（第2页）

• 展示LG-Y模型下的讨价还价区间，横轴为合并后股权价值$\muM$，纵轴为交换比率$r$。

- 阴影区域为满足双方股东期望价值增加的交换比率取值范围。

• 随着合并产生的价值增大，讨价还价区间逐渐扩大，交换比率的上下限曲线逐渐分离。

- 强调协同效应越大，双方接受的交换比率范围越丰富，有助达成合并协议[page::2]

图2（第7页）

• 展示基于Kulpa区间图示法，将$B\mathcal{R}\mu(\muM)$讨价还价区间映射为$(x,y)$点构成的参数曲线$\gamma$（双曲线）。

- $x,y$分别为区间中心、中点对称半径。

• 曲线的相关参数$\alpha1, \alpha2$与标的股权价值及交换比率相关。

- 有两条对称渐近线，图示第一象限满足经济意义，体现价值层面可接受ER集合。

• 结合股权价值关系$\muB > \muA$对双曲线位置的影响阐述了曲线形态[page::7]

图3-7（第9-13页）

• 分别对应不同条件下的讨价还价区域（BR）或一致性区域（CR）的Kulpa图示。

- 图中黑色曲线代表价值区间折射曲线，红色曲线代表风险区间折射曲线。

• 蓝色经过点与线段为两区间的交集，即最终考虑价值与风险共同约束下的交换比率接受区间。

- 图3对应Case 1（$CRB$），蓝线为双方股东在价值与风险维度上的可接受ER区间。

• 图4对应Case 2（$B\mathcal{R}\mu$），价值维度主导约束，风险维度区域较大。

- 图5对应Case 3（$B\mathcal{R}\rho$），风险维度主导约束，价值维度区域较大。

• 图6对应Case 4（$CRA$），两维约束相互限定形成的CR。

- 图7呈现无交集（空集）情形，即无可接受ER区间，暗示协同收益或风险改善不足以达成双方共识。

• 图中横轴“mid point”即区间中点，纵轴“radius”即区间半径[page::9-13]

---

四、估值分析

• 虽然本报告主要理论建模阐述，但隐含估值思路为：

- 交换比率由合并后企业价值$\muM$及风险$\rhoM$决定，是协同效应与风险调整收益风险权衡的结果。
- 采用基于价值和风险的区间边界分别定义估价上下界。
- 价值估计基准为LG-Y模型，假定价值基于股价股数乘积，且以分红贴现模型为准绳（Gordon-Shapiro模型）。
- 风险估计依赖于相干风险度量理论（Artzner等），允许应用多种度量。
- 交换比率界定受股东风险偏好、协同增值、风险降低程度驱动，且存在清晰的几何表达与解析式。

• 该方法非传统现金流折现或市盈率倍数估值，而是结合股东财富风险调整的量化讨价还价区间分析，是一种定价与谈判交叉的新颖思路[page::1-4]

---

五、风险因素评估

• 报告聚焦的风险要素是合并后股权价格的随机性及相关风险度量。

- 风险因素带来了股东接受交换比率的上界和下界差异，引入风险使得交易谈判更复杂。

• 风险可视为不确定性或波动性，带来额外考量，非单纯价值提升可接受所有ER。

- 风险度量作为非负函数$\varphii$，符合相干风险测度标准，体现风险调整的合理性和严谨性。

• 风险减小必须满足$\rhoM$在一定区间，不能低于两个公司的最大风险，说明风险改善存在限制。

- 风险增加则会缩小甚至合并后无可接受区间（见图7），即合并失败风险。

• 风险与价值权衡下，交换比率谈判形成复杂的取舍，此机制在传统文献中被忽略，是本文重点贡献之一。

- 报告针对风险的识别、影响均以数理和几何方法明确表达，增强理论深度与实用指导价值[page::2-5,13]

---

六、批判性视角与细微差别

• 优势：

- 第一篇将风险度量引入交換比率讨价还价区间的理论扩展。
- 以图式方法将二维空间的区间转化为点，解决可视化表达难题。
- 清晰揭示股东A和B在风险/收益权衡下对交换比率互相相反的激励。
- 数学推导严谨，兼顾确定性和随机性分析。

• 局限：

- 模型较为理论化，未给出实证案例验证。
- 假设股价随机变量虽无分布限制，但实际风险度量和参数估计复杂。
- 将整体股票价值风险粗化为单个风险度量存在简化，未考虑风险共轭、组合效应等。
- 设定股东接受区间所基于的风险偏好假设未完全明确，未涵盖效用理论完整框架。
- 要求同时存在协同效应与风险降低才有非空讨价还价区，实际金融市场并不总满足，导致建议理论模型有一定理想化色彩。
- 图表中的六种案例虽描述完备，但报告对各参数变化敏感性分析有限。

• 细微差别：

- 文章在不同章节对股东偏好表达有时用不严谨语言（如“希望$r$越小或越大”）但数学表达准确。
- 文档表格格式存在缺陷，可能影响阅读连贯性。
- 文中对Kulpa图示在金融场景应用的讨论较少，理论方法引用较多，实操解释稍显不足。

---

七、结论性综合

本文成功将LG-Y确定性股票换股交换比率模型扩展至包含风险度量的随机环境，明确定义并刻画了基于价值提升和风险减小双重约束下的讨价还价区域。通过引入相干风险度量及建立风险调整交换比率上下界，实现了股东期望收益和风险承受的平衡权衡。

核心贡献在于：

• 确定了双重边界：对价值和风险两维度股东均有上下界约束，分别形成$B\mathcal{R}\mu$和$B\mathcal{R}_\rho$两大区间，讨价还价区域为二者交集。

- 利用区间图示变换（Kulpa方法）将二维区间映射为二维坐标点，展示区间形态演变：通过参数曲线$\gamma, \delta$（两条双曲线）及交叉区间图形，直观显示各经济条件下讨价还价区间的变化和结构。

• 揭示风险因素对交换比率影响的反直观性质：

- 收购方股东倾向于较低交换比率以获得较大权益份额及协同收益，但风险上升实际带来对交换比率的下界要求。
- 被收购方股东则相反。

• 给出协同效应大小和风险降低幅度对可接受交换比率区间的明确数学阈值，说明交易难易度与合作成效量化关联，完善现有并购定价理论框架。

- 指出现实金融市场中该模型的理想化假设及其作为进一步研究基础的价值，包括将来可借助期望效用等更全面投资者行为理论扩充。

• 图形展示为重要创新点，在处理多维经济量度的谈判问题上提供了洞察力和可视化手段。

综上，报告为并购中风险调整的股票换股协议定价问题提供了新颖且扎实的理论基础，融合现代风险理论与可视化技术，具有较高学术价值和潜在应用意义[page::0-22]。

---

参考文献（摘要中部分）

• Larson, K.D., Gonedes, N.J., “Business combinations: an exchange ratio determination model,” The Accounting Review, 1969.

- Yagil, J., “An exchange ratio determination model for mergers: a note,” Financial Review, 1987.

• Artzner, P. et al., “Coherent measures of risk,” Mathematical Finance, 1999.

- Kulpa, Z., “Diagrammatic representation of interval space,” Reliable Computing, 1997.

• Damodaran, A., Damodaran on valuation, 2008.

---

如需更具体章节数值解析和扩展讨论，请告知。

报告