• 报告背景与目标 [page::1][page::2]：

- 深度学习为金融模型，尤其是波动率模型定价和校准提供新工具，但黑盒特性带来解释性不足。
- 粗糙波动率模型（尤其粗糙Heston模型）因更好拟合实际波动率路径及ATM隐含波动率斜率而受关注。
- 旨在构建神经网络实现从隐含波动率曲面到粗糙Heston模型参数的逆映射，并开展可解释性分析。

• 粗糙Heston模型及参数区间设定 [page::4][page::5][page::6]：

- 模型包含6个参数：$\rho, V0, \kappa, \theta, \nu, H$，其中$H \in (0,0.5)$表示路径粗糙度。
- 对参数空间设定不同范围（窄区间与宽区间）进行训练集生成，采用均匀采样合成1万组隐含波动率曲面数据。

• 神经网络结构与训练细节 [page::7][page::8][page::9]：

- 采用简单的前馈全连接网络（两层，ELU激活），输入54维隐含波动率特征，输出6个模型参数。
- 输入预处理包含归一化与ZCA白化，消除相关性和协方差差异。
- 训练采用平均对数方差损失函数，ADAM优化器，批量训练模式，训练精度高达约92%-99%。

• 预测性能与误差分析 [page::9][page::10][page::11]

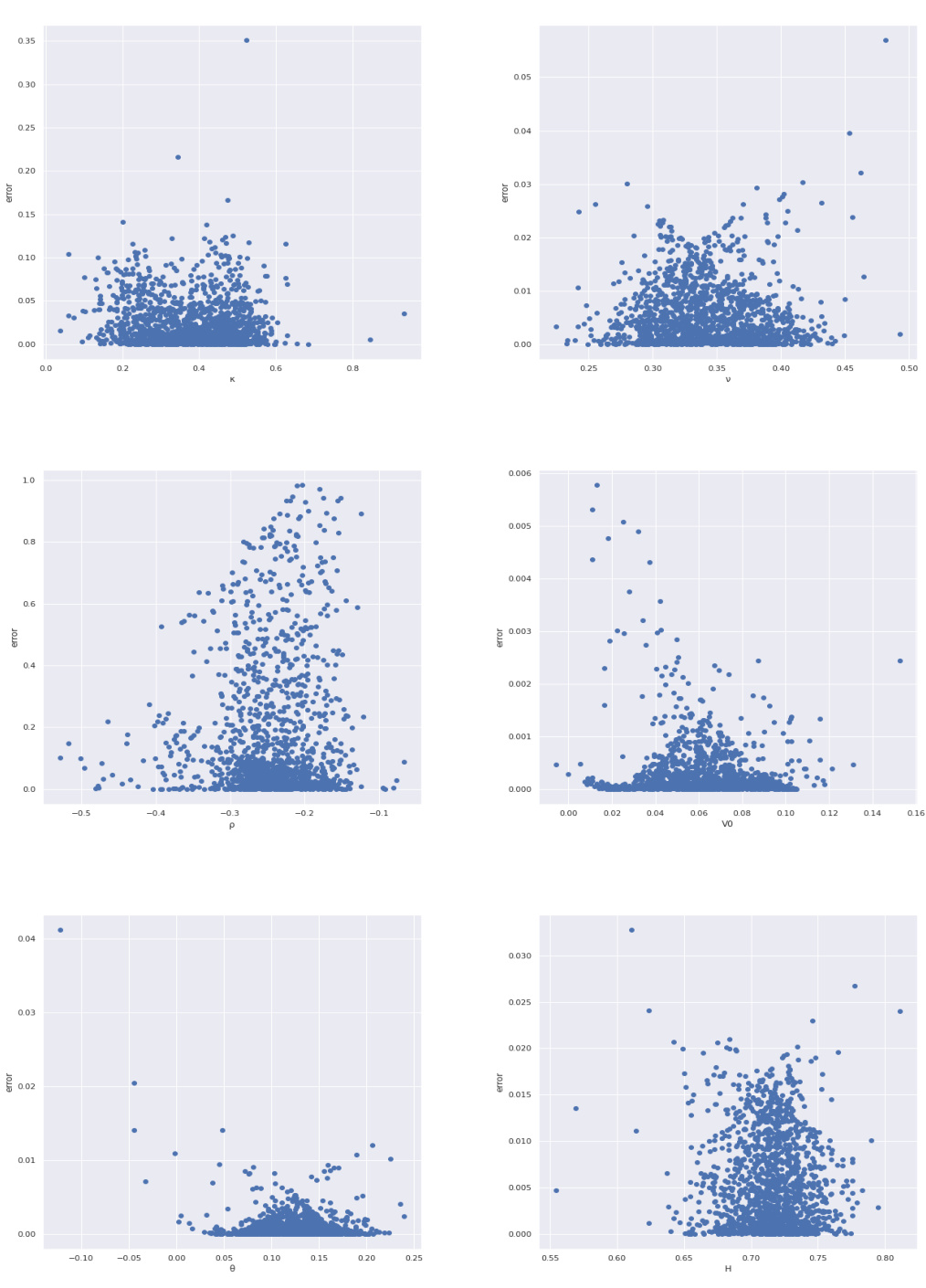
- 窄参数范围模型对$\kappa$与$\rho$参数预测误差较大，宽范围模型整体预测误差有所上升但泛化能力增强。
- 测试集及部分离样本数据均衡展示参数预测误差，部分参数存在离群点。
| 参数 | $\kappa$误差 | $V0$误差 | $\rho$误差 | $\theta$误差 | $\nu$误差 | $H$误差 |
|------|-------------|-----------|-----------|-------------|-----------|----------|
| 窄范围测试集 | 0.0014 | 0.0003 | 0.00000003 | 0.00003 | 0.0002 | 0.0007 |
| 宽范围测试集 | 0.0111 | 0.005 | 0.000 | 0.0003 | 0.0008 | 0.0055 |

• 本报告深入使用多种可解释性技术进行局部和全局分析：

- LIME显示深实值短期隐含波动率是预测$\kappa$等参数的关键贡献项。

- DeepLIFT和LRP方法一致揭示，对$\kappa$和$\nu$，重要波动率区域集中在低行权价和短到中期。



- SHAP全局解释辅助确认以深实值与短期波动率为关键，且不同参数对应不同重要区域。

• 粗糙Heston模型与经典Heston模型解释性对比 [page::19][page::20]

- 经典Heston模型局部解释多聚焦于短期但不特定于实值或虚值，粗糙Heston则明显侧重深实值短期期权隐含波动率。
- 这与粗糙波动率引起的左翼隐含波动率陡峭度显著更大相吻合。
- 表6和表7体现多方法的一致性，显示粗糙Heston模型可解释性体现其特有波动率行为。

• 未来工作与结论 [page::21]

- 下一步计划将方法推广至真实市场数据，解决真实数据噪声对可解释性的影响。
- 深度学习中的非局部非线性特征使得局部与全局解释方法互补，需进一步研究理解差异。
- 本研究为在金融模型定价和风险管理中安全可靠地使用深度学习提供了重要理论基础。

• 总结图表：

深度学习可解释性在粗波动率模型中的应用 —— 综合报告详尽分析

---

一、元数据与报告概览

报告标题： DEEP LEARNING INTERPRETABILITY FOR ROUGH VOLATILITY
作者： Bo Yuan, Damiano Brigo, Antoine Jacquier, Nicola Pede
发布机构及联系信息： 作者隶属剑桥大学Judge商学院、伦敦帝国理工及Mediobanca等著名机构。
主题： 本文聚焦于金融市场中的粗波动率模型（特别是粗Heston模型）与深度学习技术的结合，重点探讨深度学习模型的可解释性。
核心论点与主要信息：

• 尽管深度学习在金融定价与模型校准中日益普及，其“黑箱”特征令风险监控和模型理解变得困难。

- 文章提议结合多种可解释性工具，辅助理解神经网络所学习的模型参数与隐含波动率（跨期权执行价格和到期日）的映射关系。

• 以粗Heston模型为例，利用深度神经网络反演粗波动率模型参数至隐含波动率曲面，深入剖析其可解释性。

- 目标包括为该领域构建更安全的神经网络使用框架，推动定量金融模型的透明度和风险控制水平。

---

二、逐节深度解读

1. 引言

文学综述指出，在过去十年深度学习技术大幅推动了金融行业的创新，特别是在定价和校准被广泛使用的随机波动率模型方面。传统模型局限性（尤其在拟合ATM斜率方面）催生了粗波动率模型研究。尽管后者更精准，但计算复杂度增大。深度学习因能突破计算瓶颈而受关注，但其“黑箱”性质导致参数和价格映射难以直观解释。文章明确“解释性”（interpretability）概念虽无统一数学定义，但为提升神经网络在金融的应用安全性和风险监控十分关键，本文将围绕此展开研究[page::1]。

2. 可解释性分析简介

• 定义与分类

- 本地可解释性 强调对单个预测结果的局部理解，采用简化二元化输入等方法，分析特征变量对该预测的影响。
- 全局可解释性 依据所有预测，通过Shapley值等理论，衡量特征对整体模型输出的贡献度。

• 多种可解释性工具介绍：LIME（局部模型近似和解释），Gradient\*Input，DeepLIFT，LRP（分层相关传播法），SHAP（基于合作博弈论的特征归因），其中SHAP兼顾局部与全局解释能力[page::2][page::3]。

3. 粗Heston模型神经网络校准

3.1 粗波动率模型及粗Heston模型介绍

• 传统随机波动率模型无法很好捕捉市场波动特征，粗波动率采用具有Hurst指数$H \in(0, 1/2)$的分数布朗运动，捕捉标的资产价格路径的“粗糙”性质。

- 文章重点考察粗Heston模型，这一模型在无限维设定下保持了经典Heston的仿射性质，因此欧式期权定价仍可通过傅里叶变换方法实现。其参数集合为$\{\rho,V0,\kappa,\theta,\nu,H\}$，分别代表相关系数、初始方差、均值回复率、长期均值、波动率波动率和Hurst指数[page::4][page::5]。

3.2 神经网络校准方法

• 任务定义为拟合参数到隐含波动率曲面的映射，利用前馈神经网络（FNN）反演该过程。通过对广义参数空间内均匀采样生成$N=10^4$个样本，计算对应的隐含波动率，以最小化均方误差（MSE）为目标训练神经网络。

- 参数范围分为“窄范围”（基于实际SPX数据实践）及“宽范围”（在窄范围上拓展40%），并设置更广泛的外推范围用于泛化测试。训练采用Adam优化器，输入隐含波动率数据经过多种预处理（缩放、白化）以实现训练稳定[page::6]。

3.3 数据集构造

• 选择$moneyness \in \{0.6,...,1.4\}$，到期时间$T\in \{0.6,...,2.0\}$的网格，共54个数据点表示隐含波动率曲面。

- 样本分为85%训练集和15%测试集[page::7]。

3.4 神经网络架构

• 数据预处理采用两种缩放策略（0-1缩放与零均值单位方差化）。

- 白化采用ZCA方法去除输入特征间相关性，保留数据近原形态，确保输入协方差矩阵为单位阵。

• 网络为简单的两层全连接网络，输入层54个节点，输出6个模型参数，激活函数为ELU。

- 损失函数选用均方对数误差（MSLE），方便对数尺度下实际值与预测值的比较[page::7][page::8][page::9]。

3.5 校准效果与结果

• 训练过程快速收敛，无明显过拟合迹象，准确度达99%。

- 测试集误差显示大部分参数预测准确，其中$\nu, V0, \theta, H$误差较小，$\kappa$表现相对较差，$\rho$在外推样本预测中误差较大，表现不佳。

• 宽范围数据集训练后整体泛化能力增强，但$\kappa$及$\rho$仍为挑战，综合误差略有升高。

- 训练历史曲线平滑，验证集与训练集表现接近，筛选的网络架构表现稳定且实用[page::9][page::10][page::11]。

4. 可解释性结果分析

4.1 本地可解释性分析

• LIME分析

- 以$\kappa$为例，深度学习模型对深度实值区（ITM，特别是$K=0.6,T=0.6$）的隐含波动率权重最大，短期、实值期权对$\kappa$预测贡献尤为显著，具有广度和局部偏正相关特征。采样范围扩大并未改变此结论。

• DeepLIFT分析

- 结果显示整体归因集中在短期且深度实值期权隐含波动率，$\kappa$和$\nu$的驱动因素类似。$\rho$对应的显著归因在长期期权的深度价外区域。

• LRP分析

- 结果与DeepLIFT相似。$\kappa$和$\nu$重要性集中于短期期权，$\rho$的归因呈双翼、深度价内外各占一侧格局，而$\theta$在长期期权归因较多。

• 以上均表明深度实值短期期权在神经网络参数映射中占主导地位[page::11][page::12][page::13][page::14][page::15][page::16]。

4.2 全局可解释性分析

• 利用DeepSHAP方法，整体确认局部分析发掘的关键输入特征（以$K=0.6, T=0.6$为代表的深度实值短期期权隐含波动率）为模型输出最重要贡献源。

- 各模型参数受最显著特征影响有所不同，如$\kappa,\nu$受中期限实值期权影响较大，$\rho$得益于极短和极长期权，同时兼顾深价内和价外，$V0$主要与极短期期权相关联。

• 但也发现$\theta$与全局解读存在一定差异，全局结果显示短期期权贡献突出，提示进一步研究需厘清这一表现机制[page::13][page::17][page::18]。

4.3 综合讨论

• 这些特征归因结果与粗Heston模型参数的金融含义有一定吻合。例如

- $\kappa$（均值回复速度）理论上应对价内外价格均敏感，神经网络偏爱价内方向。
- $\nu$（波动率的波动率）影响波动率微笑幅度，模型聚焦实值区可能反映市场更强噪声吸收。
- $\rho$（标的价格和波动率的相关系数）体现波动率微笑的不对称性，其最显著输入特征分布于两翼，与理论期待一致。
- $\theta$（长期均值）及$V0$（初始方差）对隐含波动率曲面不同区间敏感性呈多样化，需要进一步梳理。
- $H$（粗糙参数）反映市场微笑曲线短期“粗糙度”，其影响主要集中于短期期权。

• 整体来看，粗波动率模型的神经网络映射注重深实值短期期权，这与粗Heston模型在短期左翼隐含波动率陡峭度领先于经典Heston模型的数学性质相一致。粗波动率模型输出特征明显区别于经典模型的均匀分布，这为可解释性分析提供了有力的数学支撑[page::15][page::16][page::19][page::20]。

---

三、图表与图像深度解读

图1（第8页）——隐含波动率曲面特征的相关性矩阵（缩放前后对比）

• 上左与上右图分别显示两种缩放方法数据的相关性矩阵，色度越深表示相关性越高。

- 下图是两种缩放方式下的数据白化效果图，主对角线为1，非对角元素趋近零，说明通过ZCA成功实现特征去相关。

• 该处理有助于避免输入冗余，提高神经网络训练稳定性[page::8]。

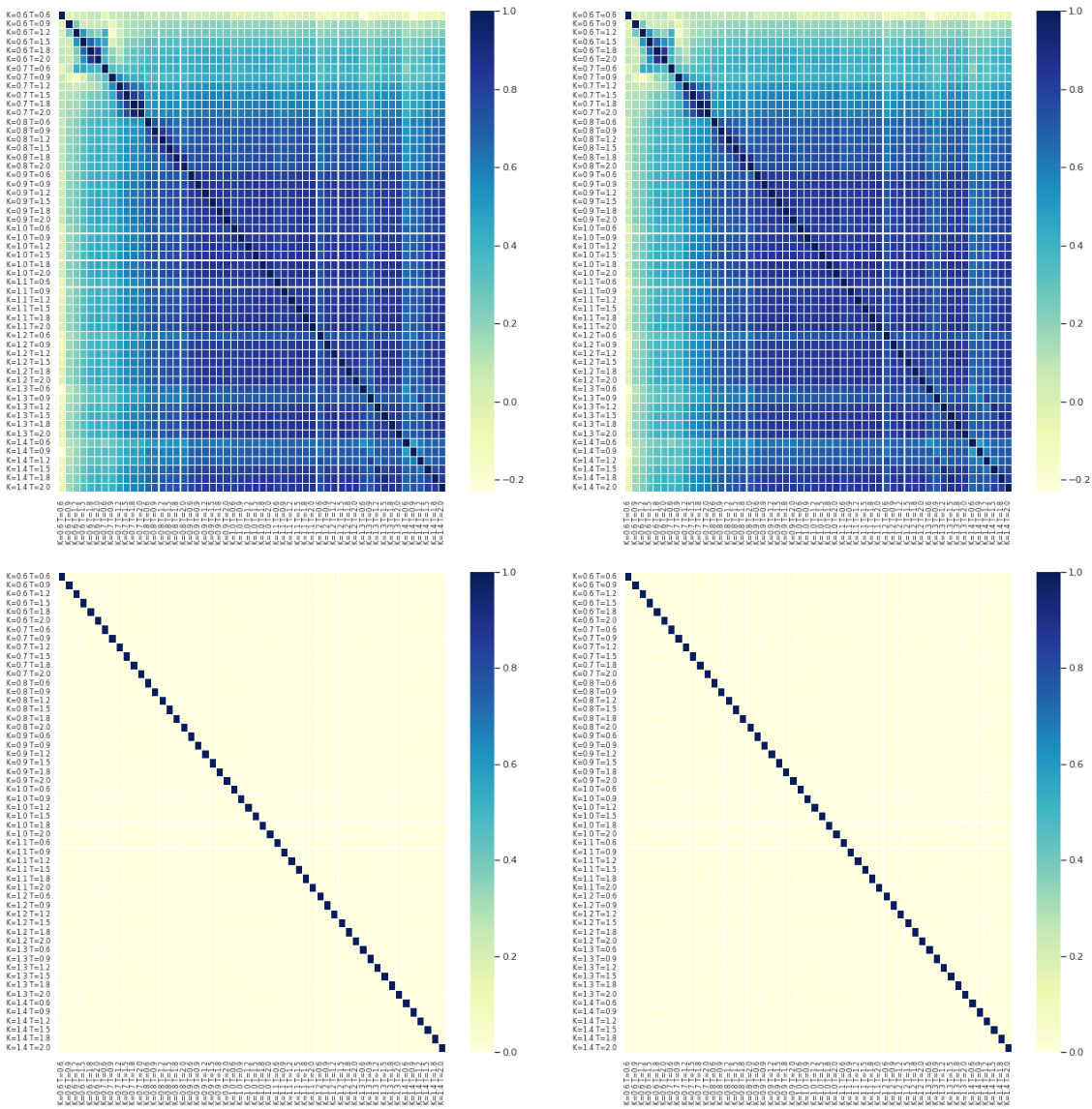
图2（第9页）——神经网络架构示意

• 结构简单，2层全连接网络；输入层54维（隐含波动率数据点数目），第1隐藏层6个神经元，输出层6维，分别对应模型六参数。

- 用ELU激活函数，利于加快收敛并防止死神经元。该架构易训练且效果在此场景足够，避免过拟合问题。

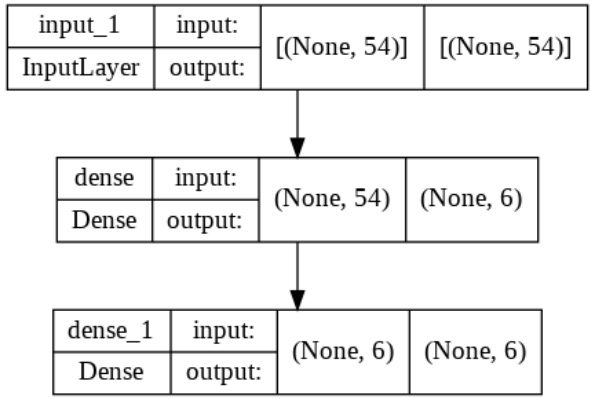
图3（第9页）——训练与验证过程准确率与损失曲线

• 从Epoch0到14，训练和验证准确率均快速上升至接近1，损失函数同步下降，显示无过拟合现象。

- 表明数据预处理、网络结构与训练策略基本匹配。

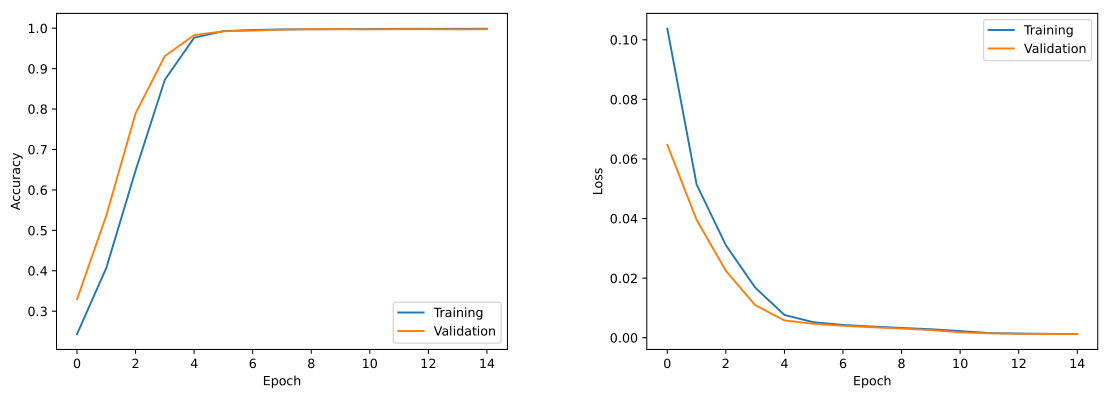
图4（第11页）——广泛参数区间训练历史

• 虽然准确率相对前述略低（约92%），曲线走势平滑，验证与训练表现一致，训练过程稳定。

- 证明对更宽参数输入分布，模型依然具备良好的泛化能力。

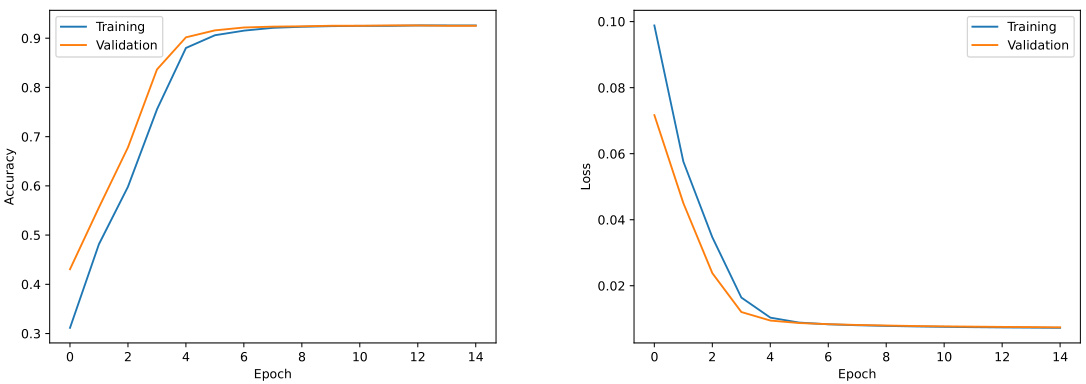
图5与图6（第12页）——LIME局部归因示例

• 图5为$\kappa$参数在单点的局部预测归因，显示深实值短期期权（$K=0.6,T=0.6$）对预测影响最大，特征贡献呈积极偏向。

- 图6为对1500个个体样本特征归因绝对值的均值热力图，突出实值较深与较短期波动率的关键地位。

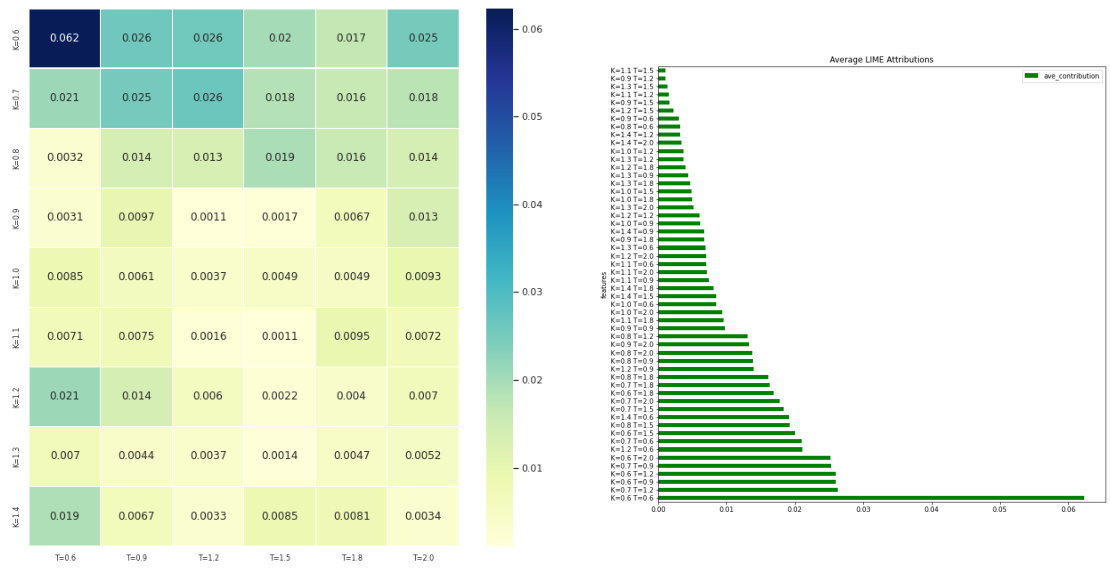
图7与图8（第13-14页）——DeepLIFT归因与参数分类贡献

• 整体DeepLIFT展示隐含波动率贡献主要在左翼（实值深处）短期期权。

- $\kappa$、$\nu$归因显著集中在短期深实值，$\rho$则显相关于长端价内外边界。其他参数表现则较为分散但有其专注区域。

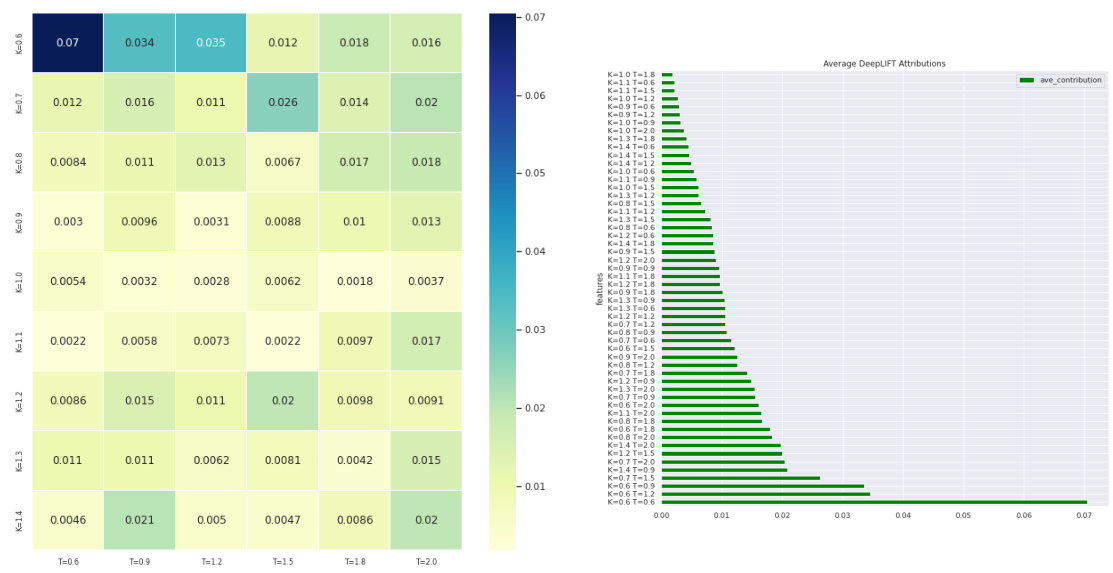
图9与图10（第15-16页）——LRP归因热图与参数归因差异

• 归因集中于短期波动率，$\kappa,\nu$对应长端权重较大，$\theta$与$H$在短期有显著权重。

- $\rho$和$V0$的归因分布略有不同，$\rho$更集中于极端短期两翼。

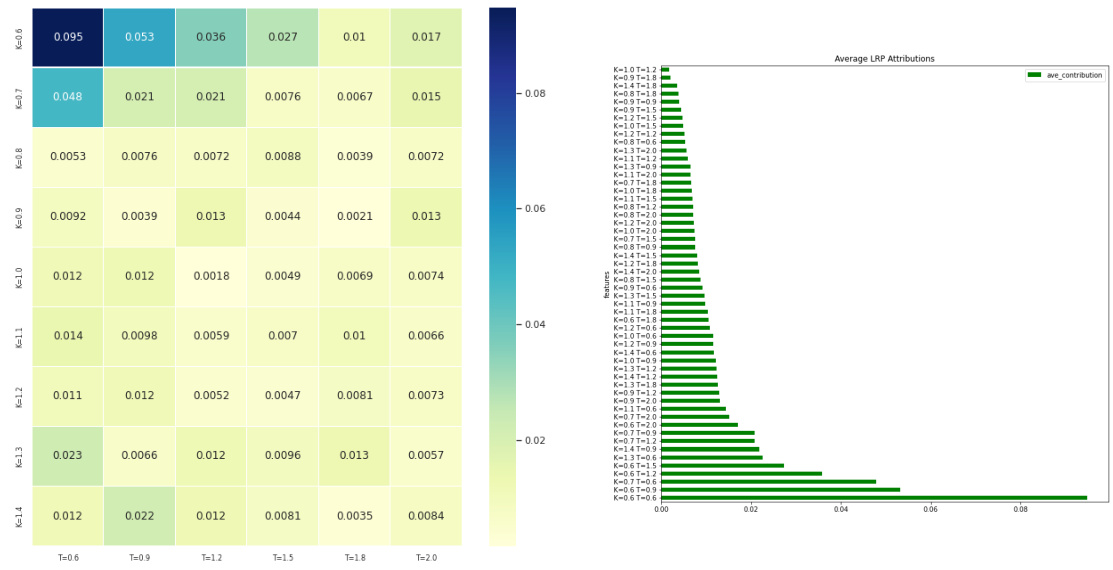
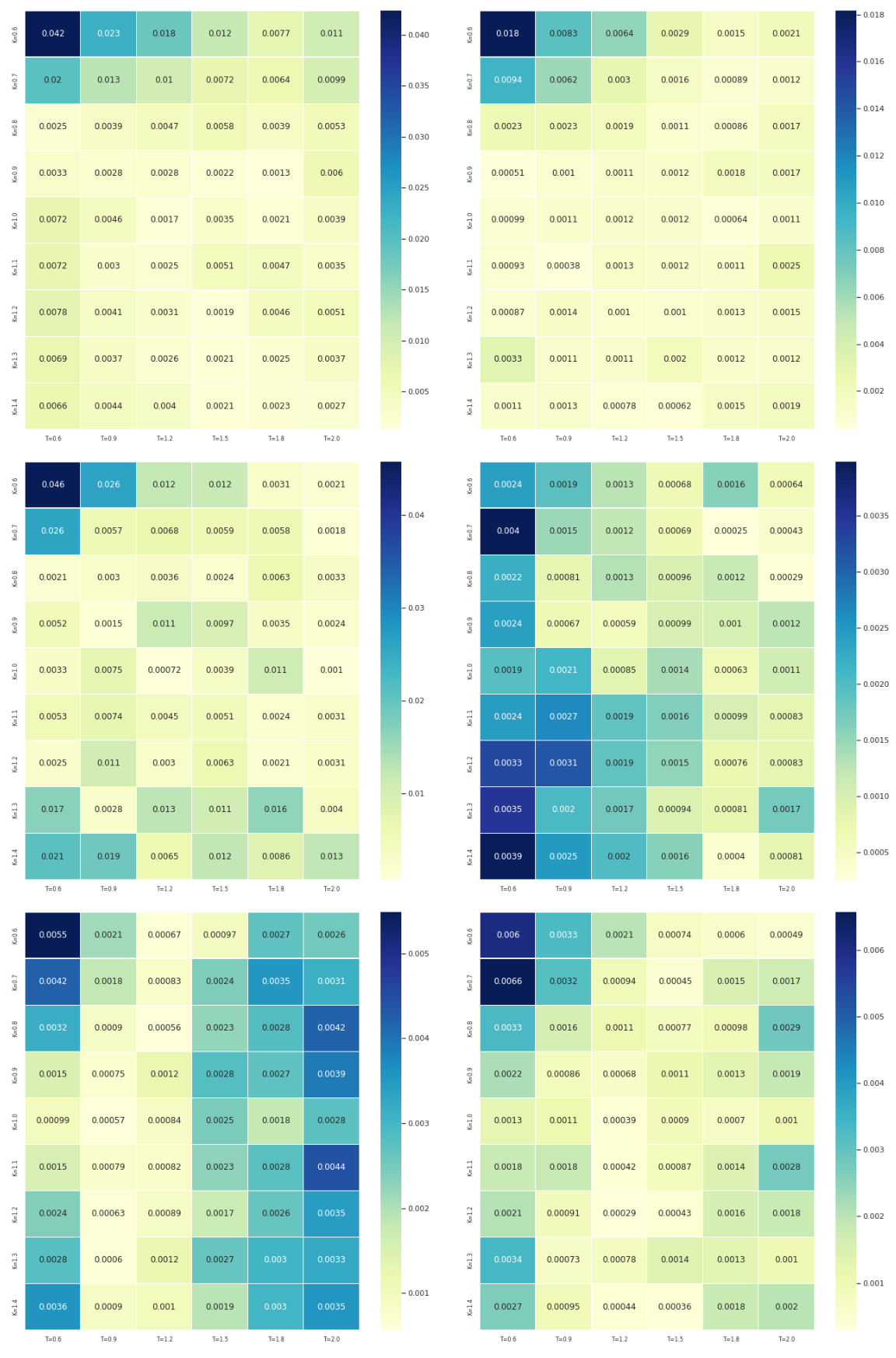
图11与图12（第17-18页）——SHAP整体特征重要性与参数影响分布

• SHAP确认深实值短期期权（$K=0.6,T=0.6$）为总体模型最重要特征。

- 不同参数对应不同特征偏重，$\kappa,\nu$侧重中期限价内，$\rho$偏好极端期限两翼，$V0$关联极短期限。

• 特征值（热度）与模型输出影响有颜色编码说明，体现各特征高低取值对应预测结果倾向。

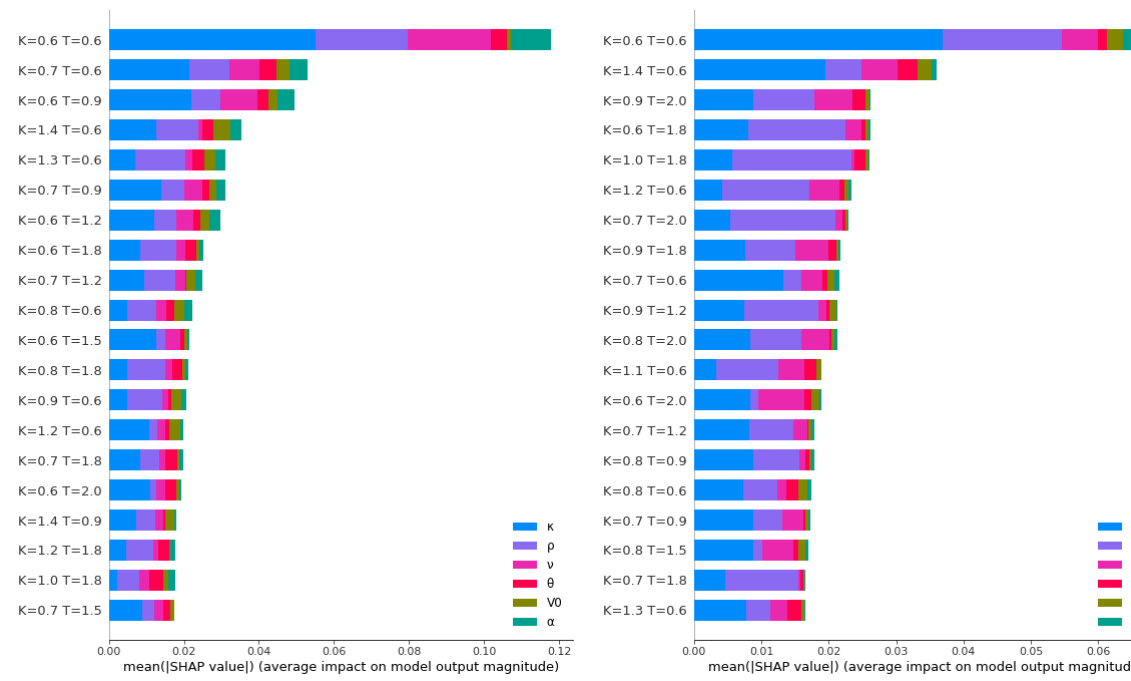
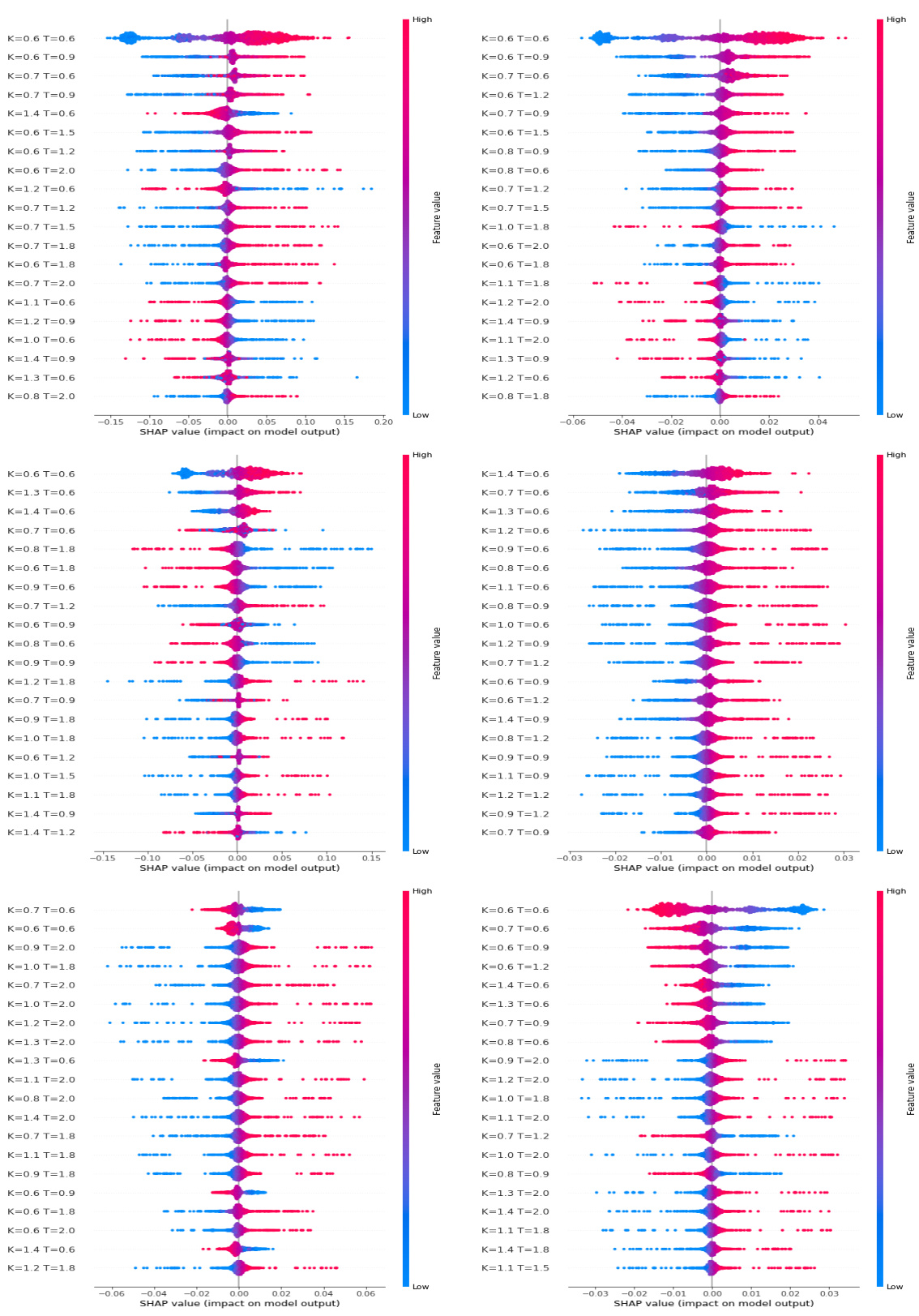
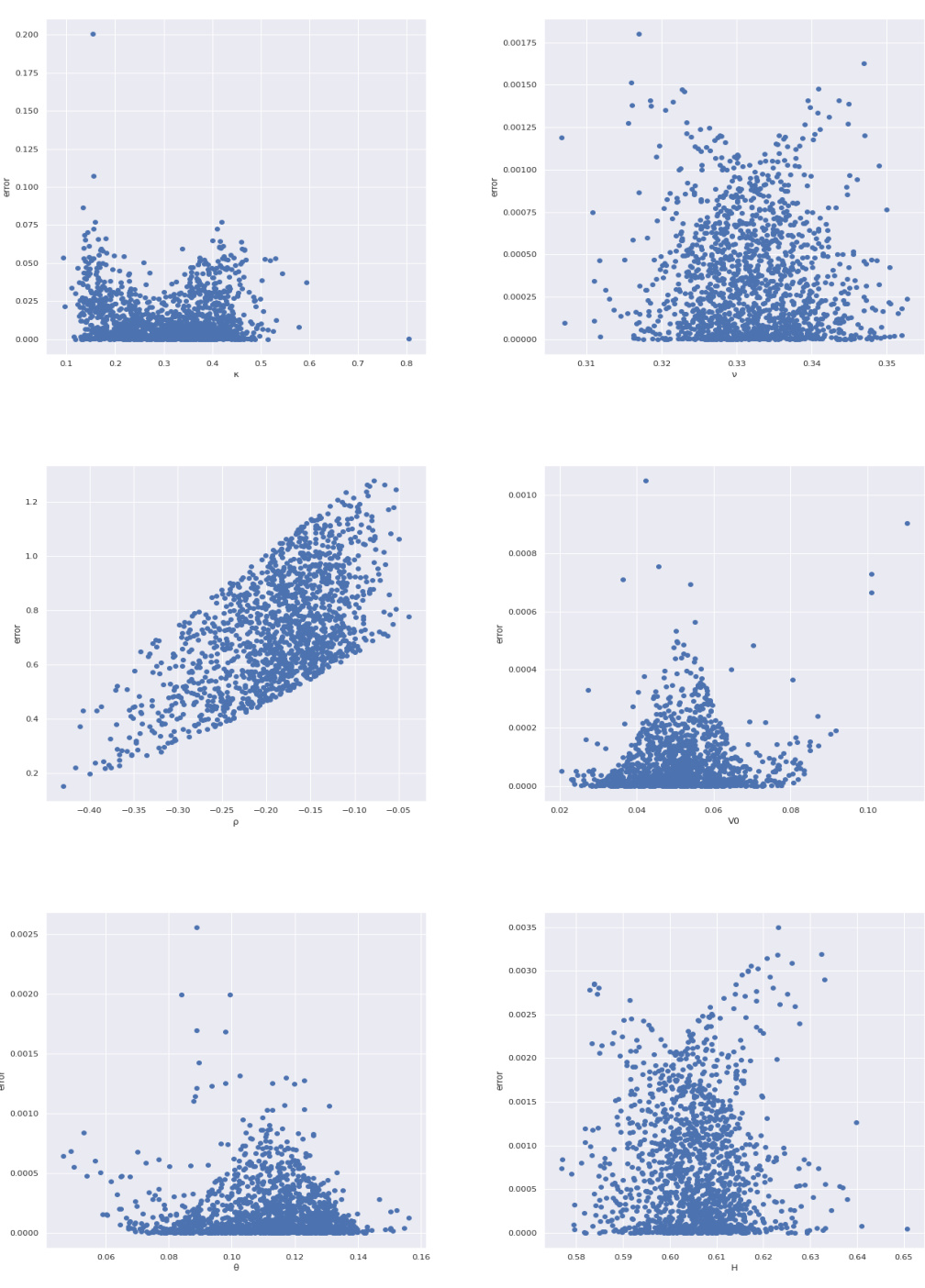
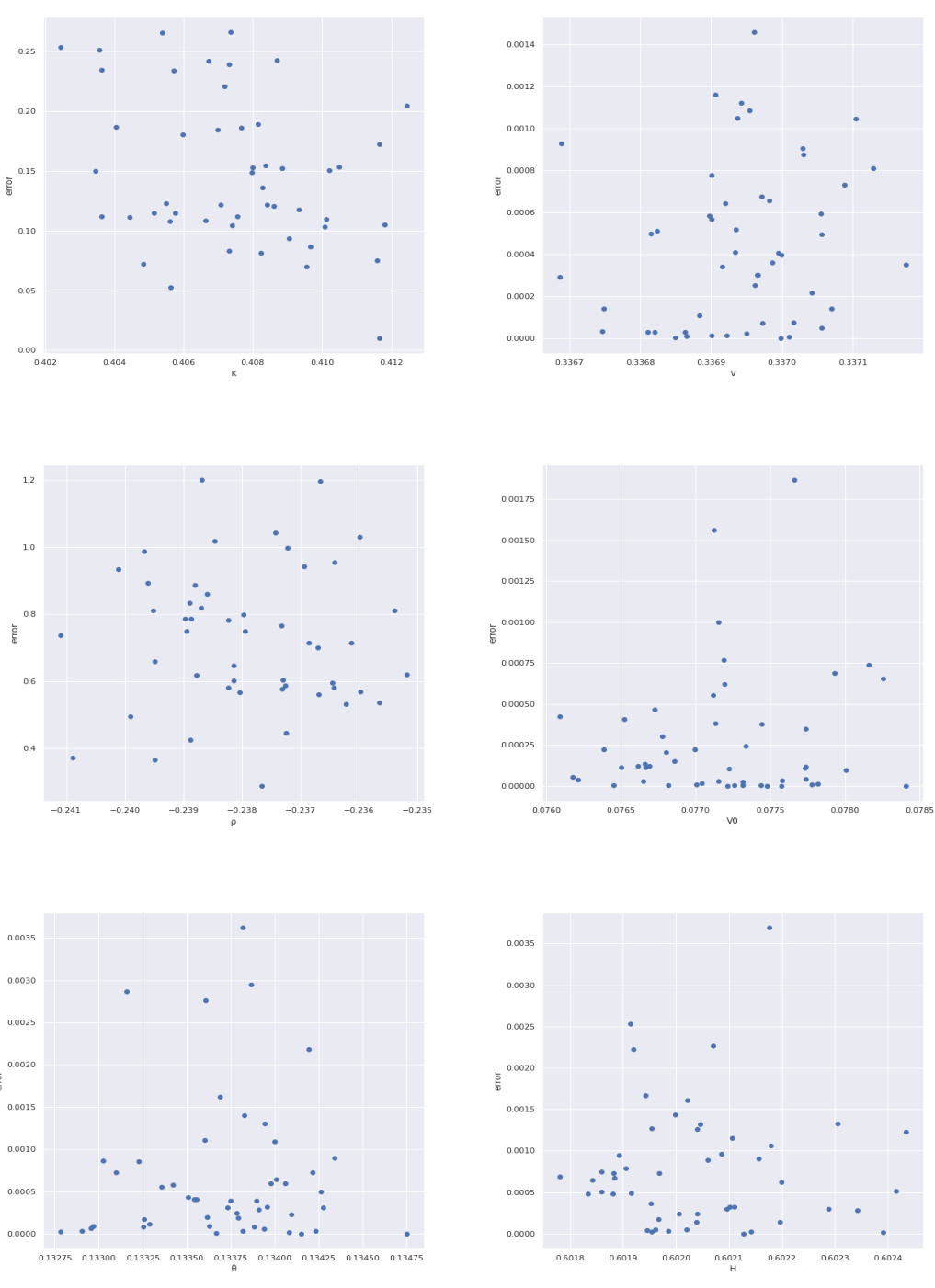
图13至图15（第23-25页）——预测误差散点图

• 图13展示测试集的单参数预测误差散点，除$\rho$和$\kappa$外，误差普遍较小。

- 图14为外推样本预测误差，$\kappa,\rho$误差明显上升，表明模型外推能力不足。

• 图15为宽参数区间下的误差，整体误差增大，但预测稳定性有所改善。

---

四、估值分析

本文无传统估值部分，核心为模型参数到隐含波动率的映射及反演。重点讨论神经网络训练目标函数（均方对数误差）以及误差评估，未采用显式折现或市盈率等典型估值方法。模型的性能评价基于参数预测误差和泛化能力。

---

五、风险因素评估

文章未直接列出风险评估专节，但可推断：

• 神经网络在参数范围外（外推区域）的表现不佳，尤其是$\kappa$和$\rho$，提示模型泛化风险。

- 模型假设粗Heston为真实机制，若市场真实动态偏离，模型拟合与解释可能失效。

• 数据采用合成样本，实际噪声数据和市场缺陷未完全纳入，影响模型稳定性。

- 可解释性方法本身也存在局限，不同方法关注维度不同，可能产生解释不一致。
报告建议结合多方法综合评估，以及未来引入真实数据和更稳定的全局可解释性技术以降低此类风险[page::19][page::21]。

---

六、审慎视角与细微差别

• 方法论依赖合成数据，尚未验证现实数据下的模型可解释性，存在现实市场噪声和结构性风险未覆盖的隐患。

- 深度学习预测$\kappa$和$\rho$表现较差，存在参数不可识别性，提示该问题可能是模型内生性质或数据限制。

• 可解释性侧重点主要集中于深实值短期期权，与传统观点（如ATM期权重要性）略有差异。此现象虽有数学解释，但亦可能是训练样本分布或数据预处理造成的偏向。

- 局部与全局可解释性结果大致一致，但局部解释依赖轻度线性化假设，可能无法覆盖高非线性区域，准确性受限。

• 不同可解释性工具（LIME, DeepLIFT, LRP, SHAP）均有自身算法偏差，单一方法结果需谨慎解读。综合多法论证更鲁棒。

- 报告未直接针对神经网络选择结构深度与宽度的比较分析，可能存在结构改进空间，尤其是针对参数辨识能力低的领域[page::15][page::19][page::21]。

---

七、结论性综合

本文通过粗Heston模型案例，系统性地结合深度神经网络校准与多种可解释性方法，取得以下关键发现：

• 模型拟合：一层含ELU激活函数的前馈神经网络结构，结合合理的数据缩放和白化处理，能够高效且准确地反演粗波动率模型参数，并在限定参数范围内实现超过90%的准确率。

- 参数识别：$\nu, V_0, \theta, H$等参数预测较为稳定且误差较低；$\kappa$及相关系数$\rho$存在较大预测误差，特别在参数外推时表现较差，表明这两参数的辨识性和泛化性仍为难点。

• 可解释性发现：LIME、DeepLIFT、LRP等局部方法和SHAP全局方法均表明深实值（ITM）短期期权隐含波动率对模型参数的影响最大，尤其表征粗Heston模型短期期权隐含波动率左翼陡峭特征。

- 对比经典Heston模型：粗Heston模型的可解释性聚焦点明显偏向深实值和短期隐含波动率，与经典模型中较均匀的关注度分布截然不同。粗波动率的数学理论支持这一现象，提升了本研究结论的稳健性。

• 可解释性的金融意义：通过解码神经网络映射，帮助理解参数对隐含波动率结构的定量贡献，辅助金融专家更好地把握模型风险及参数调整对市场定价的影响，为未来深度学习在金融定价与风险管理中的实用性奠定基础。

- 后续展望：将试图应用于真实市场数据，评估在含噪声和市场非理想性环境下的表现与可解释性；推进全局解释方法的发展以弥补局部方法局限；探索提高关键参数识别力的网络架构与损失函数设计。

综上，本报告为粗波动率模型结合深度学习技术的可解释性研究提供了详尽理论基础与实证分析，提升了该领域模型透明度和可信度，对金融工程与量化风险管理具有显著指导价值。[page::1][page::9][page::15][page::19][page::21]

---

参考图示（部分）

• 图1：数据白化前后相关性矩阵对比

• 图2：前馈神经网络结构示意

• 图5与图6：LIME局部归因分析实例

• 图7与图8：DeepLIFT归因

• 图11与图12：SHAP重要性与特征-输出关系

---

以上为报告内容的详尽解读与全面评估，基于文本、数学公式及图表逐一解构，力求帮助金融研究与实践人员深入理解深度学习在粗波动率模型中的作用、可解释性成果以及未来研究方向。

报告