• 机器学习模型在风险溢价预测中表现突出，显著超越传统OLS与基准因子模型 [page::1][page::5]

- 以神经网络对S&P 500进行市场时点预测，年化Sharpe比率达0.77，高于买入持有的0.51。
- 通过股票层面的神经网络预测构建多头-空头组合，年化Sharpe比率最高达1.35（价值加权），相较传统回归提升超100%。

• 机器学习方法定义及优势 [page::2][page::3]

- 机器学习结合高维统计模型、正则化和高效算法，可处理数百个高度相关预测变量。
- 其灵活的非线性和交互效应建模能力，有效应对资产定价过程中函数形式不确定的问题。

• 细节方法介绍和性能评价 [page::7][page::9][page::11][page::15][page::17][page::19][page::21][page::23]

- 比较了线性模型、弹性网络、主成分回归（PCR）、偏最小二乘（PLS）、广义线性模型、回归树（包括梯度提升和随机森林）与神经网络。
- 采用分割样本进行训练、验证和测试，使用Huber loss提升鲁棒性，利用Diebold-Mariano检验进行模型间统计比较。

• 实证样本和特征设计 [page::25][page::26]

- 样本长期覆盖1957-2016年，约3万只股票。
- 特征包括94个股票特性、74个行业哑变量及8个宏观变量，交叉形成920维特征向量。

• 预测性能对比及模型复杂度 [page::27][page::28][page::29]

- 全样本股票预测，OLS全变量模型表现差（$R^2{oos}=-3.46\%$），而神经网络（NN3）最高达到$0.40\%$。
- PCR、PLS和树模型表现次之，广义线性模型没有明显优势。
- 神经网络中浅层（最多三层）表现优于更深层。

• 变量重要性分析 [page::31][page::32][page::33][page::34]

- 所有模型一致认同最重要的特征包括价格趋势（如动量、短期反转）、流动性指标（市值、换手率、买卖价差）、风险测度（波动率、贝塔）及估值比率。

• 非线性与交互效应分析 [page::36][page::37]

- 神经网络模型（NN3）揭示了复杂交互，如规模效应受动量和波动率等指标调节，且这些效应在不同宏观经济状态下存在差异。

• 投资组合层面预测绩效及经济价值 [page::38][page::40][page::41][page::42][page::44][page::45]

- 非线性模型在市场组合及Fama-French因子组合均实现显著预测提升，NN3在所有30个组合均有正面预测$R^2{oos}$。
- 机器学习驱动的资产组合策略带来显著超额收益与夏普比率提升，如基于NN3的S&P 500市场时点策略，年化Sharpe可提升至0.77。
- 机器学习构造的多头-空头分组策略，价值加权Sharpe达到1.35，等权重甚至达2.45。
- 投资组合风险表现良好，最大回撤和单月极端亏损均优于传统模型。

• 机器学习模型叠加策略效果 [page::45]

- 简单均等加权和基于验证样本选优的元策略均进一步提高预测和投资表现，展现机器学习方法集成的潜力。

• 结论 [page::46]

- 机器学习改善了资产风险溢价的测度，神经网络和树模型因捕捉复杂非线性交互尤为突出。
- 浅层网络优于深层网络，且模型表现对大市值股票更佳。
- 预测的主要驱动变量涵盖价态动量，流动性和波动率等关键因子。
- 研究对资产定价理论建模与金融科技实践均有深远启示。

金融研究报告详尽分析报告

1. 元数据与概览

• 报告标题: Empirical Asset Pricing via Machine Learning

- 作者: Shihao Gu（芝加哥大学布斯商学院）、Bryan Kelly（耶鲁大学、AQR资本管理、NBER）、Dacheng Xiu（芝加哥大学布斯商学院）

• 发布机构与时间: 由芝加哥大学布斯商学院与耶鲁大学联合完成，编辑 Andrew Karolyi 最终决定于2019年9月22日，文章提交日期为2018年9月4日。

- 研究主题: 运用机器学习方法改进实证资产定价问题，尤其侧重于测量资产风险溢价，评估机器学习在金融资产风险定价的预测性能和经济价值。

• 核心论点: 报告系统比较了多种机器学习方法在资产回报预测中的表现，发现机器学习预测尤其是树模型和神经网络能够较传统回归模型显著提升预测精度和投资组合的经济收益，明确指出非线性变量交互是其核心优势。所有方法共同识别出动量、流动性和波动率等为主导的预测信号。

- 目标与价值: 为资产定价领域机器学习的应用设立新的表现基准，同时展现机器学习可以有效解决传统方法面临的大维度预测变量和非线性模型构建难题，从学术和实务角度对机器学习方法在资产定价中的价值和未来潜力进行深入论证。[page::0,1]

---

2. 逐节深度解读

2.1 报告引言与研究定位

• 作者定义机器学习为高维预测模型结合正则化和高效的算法搜索优化，特别强调其在解决资产回报预测时处理高维度、变量相关和模型非线性复杂度方面的优势。

- 资产风险溢价难以测量，受市场效率及随机新闻影响很大，机器学习方法的灵活性和泛化能力有助于处理实际返回的复杂结构，有望突破传统方法的瓶颈。

• 机器学习允许利用数百种股票特征与宏观变量，涵盖变量变换和交互，推动资产定价实证路径的创新。[page::2,3]

2.2 方法比较与模型描述

• 从简单线性回归（OLS）作为基准出发，阐明OLS模型在大维度和高相关变量下的局限，易过拟合且预测性能差。

- 运用正则化方法，如弹性网（Elastic Net）、主成分回归（PCR）和偏最小二乘回归（PLS）实现维度约简和参数稀疏化，显著缓解过拟合，提高预测稳定性。

• 引入广义线性模型作为非线性扩展，利用样条基函数捕捉单一变量非线性，但未涉及变量交互，未显著提升预测。

- 回归树及其集成方法（随机森林和梯度提升树）能通过树结构自适应捕获多变量非线性交互，树模型复杂度主要呈现为浅层树，符合资产定价数据量和信噪比限制。

• 神经网络模型特别重点介绍了架构设计（隐藏层数与神经元数量）、激活函数（ReLU）、优化技巧（随机梯度下降、学习率衰减、早停、批标准化及集合学习）等，对非线性交互的高度灵活拟合力显著。

- 模型训练分样本划分：训练集用于估计，验证集用于调优超参数，测试集用于最终性能评估，保证严格的样本外测试验证。[page::7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]

2.3 机器学习方法表现概览

• 对比13个不同机器学习模型在30,000多只股票，长达60年的数据中表现，衡量指标为严谨定义的样本外预测$R^2$。

- 纯OLS 全变量模型预测性能巨大下滑（负的$R^2$），显示过拟合严重。

• 弹性网、PCR、PLS等正则化线性模型提升至0.1%~0.27%区间，维度约简比仅变量筛选表现更优，表明变量间存在冗余及噪声。

- 加入非线性与交互的树模型和神经网络进一步提升$R^2$，树模式0.33%~0.34%，神经网络最佳达0.40%，三层神经网络（NN3）表现最优，层数超过三层并未带来提升，反映数据量和信噪比限制“深度学习”优势。

• 大盘股票中表现更佳，说明机器学习成果非微观流动性套利所致。

- 年度预测显示$R^2$提升显著超过月度预测，意味着机器学习模型捕获长期风险溢价信号。

• 统计测试表明神经网络在预测准确性上显著优于线性和广义线性模型，优于树模型但无统计显著优势测试。[page::26,27,28,29,30]

2.4 关键预测变量分析

• 多种变量重要性指标表明所有方法普遍认同最重要的特征涵盖四类：

1. 价格趋势相关变量：包括短期逆转(moment1m)、12个月动量(moment12m)、行业动量(indmom)、最大历史回报(maxret)等；
2. 流动性变量：市场价值(mvel1)、成交量(dolvol)、换手率(turn)、Amihud流动性指标等；
3. 风险与波动率：收益波动率(retvol)、特有波动率(idiovol)、市场beta；
4. 估值及基本面变量：如市盈率(ep)、销售增长等。

• 线性模型偏重价格趋势，树与神经网络模型重要性分布更均匀，显示非线性模型能综合利用更广泛信息。

- 宏观变量中，整体一致认定账面市值比(bm)最关键，而市场波动率较少体现。

• 交互效应探索以神经网络模型NN3为例，验证了典型股票特征如市值与动量、波动率间动态非线性交互，进一步解释非线性模型优势。

- 规模效应和动量效应在低估值、市场发行减少环境下更强，交互效应在宏观层面稳定。[page::31,32,33,34,35,36,37]

2.5 组合层面预测和经济价值评估

• 将个股预测通过加权方式聚合至30个历史重要投资组合（包括S&P500、Fama-French五因子及其子组合）。

- 机器学习非线性方法，尤其神经网络，显著提升组合预测$R^2$（如S&P 500组合中，三层神经网络预测$R^2$高达1.80%）

• 线性模型在组合层面难以超越零预测效益，树和神经网络在所有组合中普遍实现正预测。

- 通过Campbell and Thompson (2008)公式，将组合层面预测$R^2$转化为夏普比率提升，神经网络可将S&P500夏普比率从0.51提升至0.77，增幅超过26个百分点。

• 基于机器学习预测构建的市场时机投资组合展现出极佳性能，多个神经网络架构获得高达1.35（价值加权）和2.45（等权）年化夏普率的长期持有组合。

- 神经网络构建的投资组合在极端回撤、单月极端亏损及换手率方面表现优异，显示更稳健且具适当交易活跃度。

• 组合收益对传统Fama-French六因子模型具有显著Alpha和高信息比率，进一步彰显机器学习模型捕获到了传统因子模型未覆盖的收益结构和风险溢价。

- 多策略集成组合略有超越单一最优神经网络模型，但差异不显著，表明最优单模型已非常有效。

• 结果在月度和年度频率均保持稳健，一致体现非线性机器学习模型带来的经济和统计意义上的投资价值。[page::38,39,40,41,42,43,44,45,46]

---

3. 图表深度解读

3.1 表格1：机器学习模型个股预测$R^2$比较（图见页27）

• 描述：比较13种模型在全部个股、最大市值1000、最小市值1000股票子样本中的月度样本外$R^2$。

- 解读：
- OLS完整模型$R^2$大幅为负，表明未正则化的高维OLS过拟合严重，预测不及简单零预测。
- OLS3模型（3变量）保持微弱正预测能力。
- Penalized linear模型如Elastic Net提升至0.11%-0.16%水平。
- PCR和PLS进一步提升至0.26%-0.27%。
- 树模型（RF和GBRT）均达到约0.33%-0.34%，表现优于所有线性模型。
- 神经网络表现最佳（NN3至NN4），最高达0.40%。显示深层非线性交互对提高预测能力的极大贡献。
- 高市值样本中性能优于低市值样本，排除小盘股微观结构噪声解释可能。

• 联系文本：支持文本中关于OLS瓶颈和非线性模型能带来实质性预测提升的论点。

- 局限性：$R^2$极小，数据噪声高，预测仍面对挑战，且非线性深层结构未必适合过深网络，数据量成限制因素。

3.2 图3：模型逐年复杂度（水平方向时间）

• 描述：报告不同机器学习模型每年选择的特征数量、主成分数量、树深度等复杂度参数。

- 解读：
- Elastic Net变量数量从几乎无到20-40波动，符合市场变迁对模型复杂度的需求。
- PCR维度通常为20-40主成分，说明需要较多组合信号。
- PLS主成分数较少，且早期缺少显著成分。
- 树模型深度很浅，1到5层，提升树所用特征数从几十缓慢增加，反映过拟合控制与信号捕获的权衡。
- GLM虽选较多变量，但性能不及树和神经网络。

• 联系文本：说明复杂度调节对避免过拟合关键作用，浅层非线性模型更适合本领域数据特点。

3.3 表2与表3：年度预测与统计显著性测试（页30）

• 年度预测$R^2$相比月度提升数倍，神经网络优势更显著。

- Diebold-Mariano测试显示神经网络对比线性模型和GLM表现显著，但与树模型差异不大。

• Bonferroni校正后神经网络对线性模型优势稳健，对树模型边际。

3.4 图4与图5：变量重要性排名（页32-33）

• 各模型前20大变量高度一致，均以动量、逆转为首。

- 树和神经网络模型特征分布较广，给予多变量信息权重，线性模型更聚焦动量强变量。

• 宏观变量中账面市值比（bm）尤为关键，非线性模型更重视其他宏观指标如发行规模(ntis)和利差(dfy)。

- 可见机器学习模型能捕获更丰富风险因子及变动结果。

3.5 图6-8：边际效应与交互效应（页36-37）

• 报告分别展示规模、动量、波动率与应计利润的单变量边际效应，神经网络凸显非线性效应（如规模越小，预期收益越高，波动率效应亦显著）。

- 交互检验揭示规模与动量、波动率间多层次非线性关联，说明神经网络通过捕获复杂交互提升预测。

• 宏观变量调节特征效应明显，如高bm强化规模效应，高发行量增强波动率效应。

3.6 表5-8及图9：组合预测及投资绩效总结（页40-46）

• 机器学习非线性模型，尤其神经网络，实现了对广泛组合的显著预测超越，$R^2$达1%+，夏普率提升显著。

- 长短收益分组组合（decile spread）表现卓越，如神经网络4层模型等权夏普率超过2，显著优于传统模型。

• 多项风险调整指标（最大回撤、单月最大亏损、换手率）均显示神经网络模型策略稳健性优异。

- 集成方法虽稍提高预测准确率，但收益表现未优于最佳单模型。

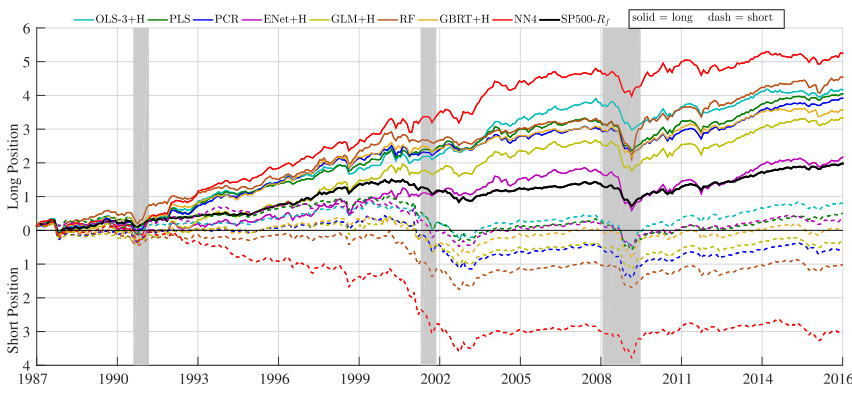
• 图9表现神经网络长短头寸累积收益远超其他模型，尤其在经济衰退期表现分化明显。

---

4. 估值分析

本报告主要评估了模型预测性能及经济收益提升，并未侧重经典的内在价值估算模型。其经济评估通过预测$R^2$转化为夏普比率提升，进而通过组合投资绩效体现机器学习模型的间接估值优势。

• Campbell & Thompson (2008)公式连接预测准确度与夏普率提升，数学表达简洁，易于理解机器学习预测对实际投资组合收益改进的效应。

- 投资组合的Alpha和信息比率结果表明，机器学习策略捕获了传统因子未充分覆盖的风险溢价，表明其对资产价格发现具增量价值。

---

5. 风险因素评估

• 该报告并未将金融市场系统性风险、模型风险等作为专门章节讨论，而是通过模型复杂度控制与样本外测试严谨性，在一定程度上规避了过拟合带来的预测风险。

- 过拟合风险通过交叉验证、正则化、早停及模型集成等技术手段得到抑制。

• 深度学习的层数限制及浅层网络优胜显示数据量和信噪比是本领域天然的风险限制因素。

- 机器学习方法本身并无因果解释能力，作者强调理解经济机制仍需结合结构模型，机器学习是辅助测量而非直接建模工具。[page::6]

---

6. 审慎视角与细微差别

• 偏见风险: 报告重点聚焦预测性能和策略收益，可能低估非稳定经济周期期间模型回撤和行为偏差风险。

- 深度学习限制: 传统观念中“深度”可显著提升表达能力，但本研究表明“浅层”神经网络反而更适合金融微观数据特征，折射出资产定价领域特有的数据制约。

• 变量选择及解释: 多种变量重要性指标一一对应，提高可解读性，但因机器学习黑箱特点，对非线性交互的实际经济含义需谨慎推断。

- 实时执行风险: 高换手率带来流动性和交易成本压力，实际应用时需结合执行策略和成本控制进一步验证。

• 模型泛化性和样本外稳定性: 尽管进行了大量样本外测试，未来环境变化可能对模型表现产生未知影响。

- 非全覆盖方法: 研究中无支持向量机或强化学习等方法，未来可进一步扩展机器学习算法库。

• 数据限制: 部分基本面变量为低频更新，可能限制部分预测变量的即时作用。

---

7. 结论性综合

本报告系统比较了多种机器学习技术对资产定价中风险溢价的预测能力，通过覆盖1957—2016年近30,000只美国股票的丰富数据，采用严密的样本划分、超参数调整与多维度检验指标。结论如下：

• 预测性能提升显著：机器学习模型，尤其是浅层神经网络和树模型，通过捕捉非线性交互特征，实现对单个股票和组合回报的统计意义和经济意义上的有力预测。

- 非线性交互为核心优势：相比传统线性模型和扩展的广义线性模型，多层神经网络(3层最佳)和集成树方法有效捕获复杂多变量关系，提升约0.1个百分点以上的样本外$R^2$，对应投资组合夏普比率提升数十个百分点。

• 变量一致性与解读价值：所有方法识别出以动量、价格逆转、流动性和波动率为核心的关键预测变量，且机器学习模型能够揭示关键变量的非线性和交互效应，丰富了经济理解。

- 组合预测与实战应用潜力强：无论是预设的经典因子组合，还是基于机器学习排序构建的投资组合，均表现出良好的预测精度和风险调整后的收益，且最大回撤和单月最大亏损显著优于传统模型，展示高度的实用性与稳健性。

• 浅层优于深层：金融领域数据样本量和信噪比限制了深度学习优势，浅层架构更适合。

- 经济机制分析仍需结合结构模型：机器学习作为预测/测量工具，尚不能完全替代解释性经济模型，但可为后者提供更精确的条件期望估计。

• 行业前景广阔：机器学习在金融资产定价的成功，证明其在金融科技和资产管理中的核心地位日益巩固，未来结合结构模型和更高级算法的潜力值得期待。

综合来看，报告清晰展现了机器学习特别是神经网络技术，在传统资产定价方法基础上的增量价值，并为金融界进一步应用和研发新型资产定价模型提供了理论与实证参考。[page::0,1,3,4,5,6,26,27,28,29,31,32,33,34,35,36,38,39,40,41,42,43,44,45,46]

---

附图精选

图1 回归树示例（页17）

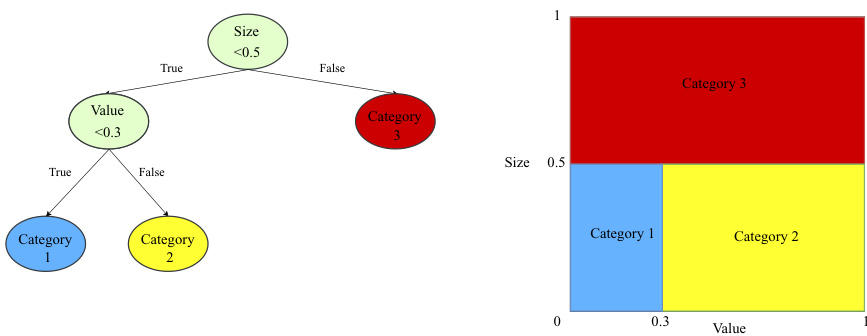
图2 神经网络结构示意（页20）

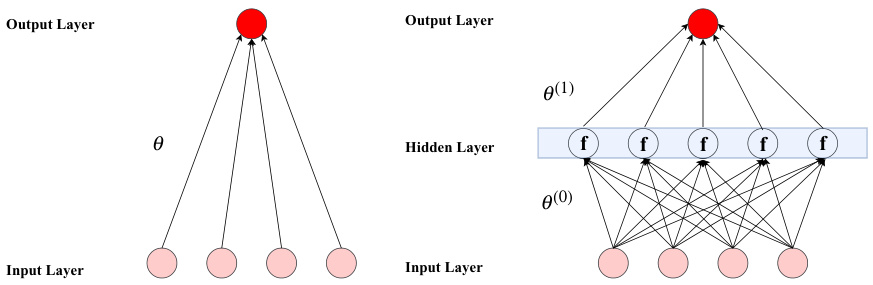
表1 机器学习方法月度个股预测$R^{2}$对比（页27）

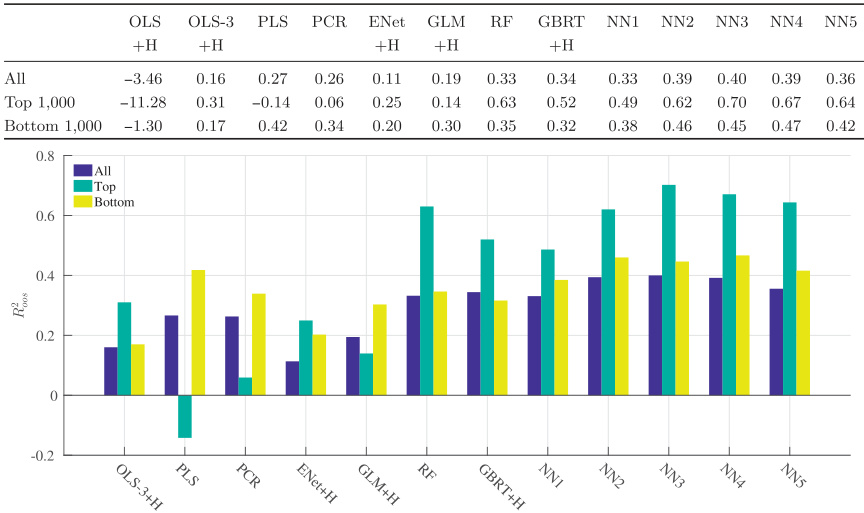
图3 模型复杂度随时间变化（页28）

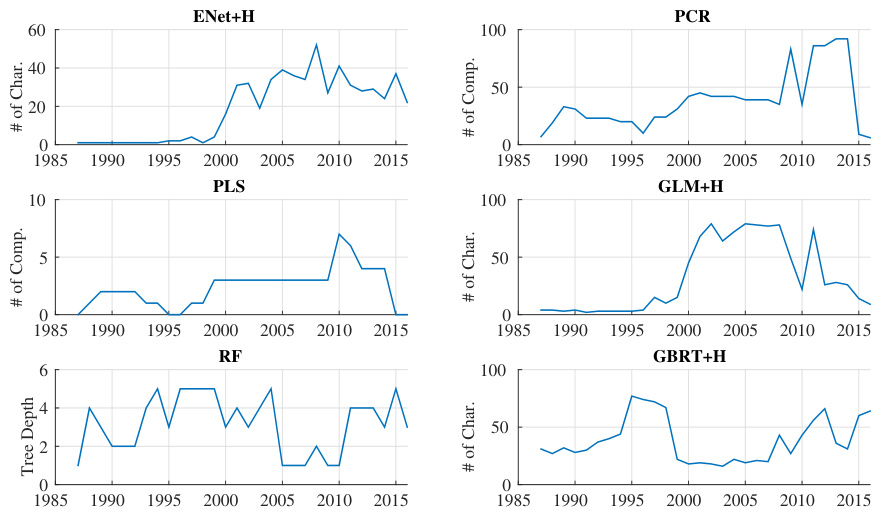
图4 不同模型变量重要性排行（页32）

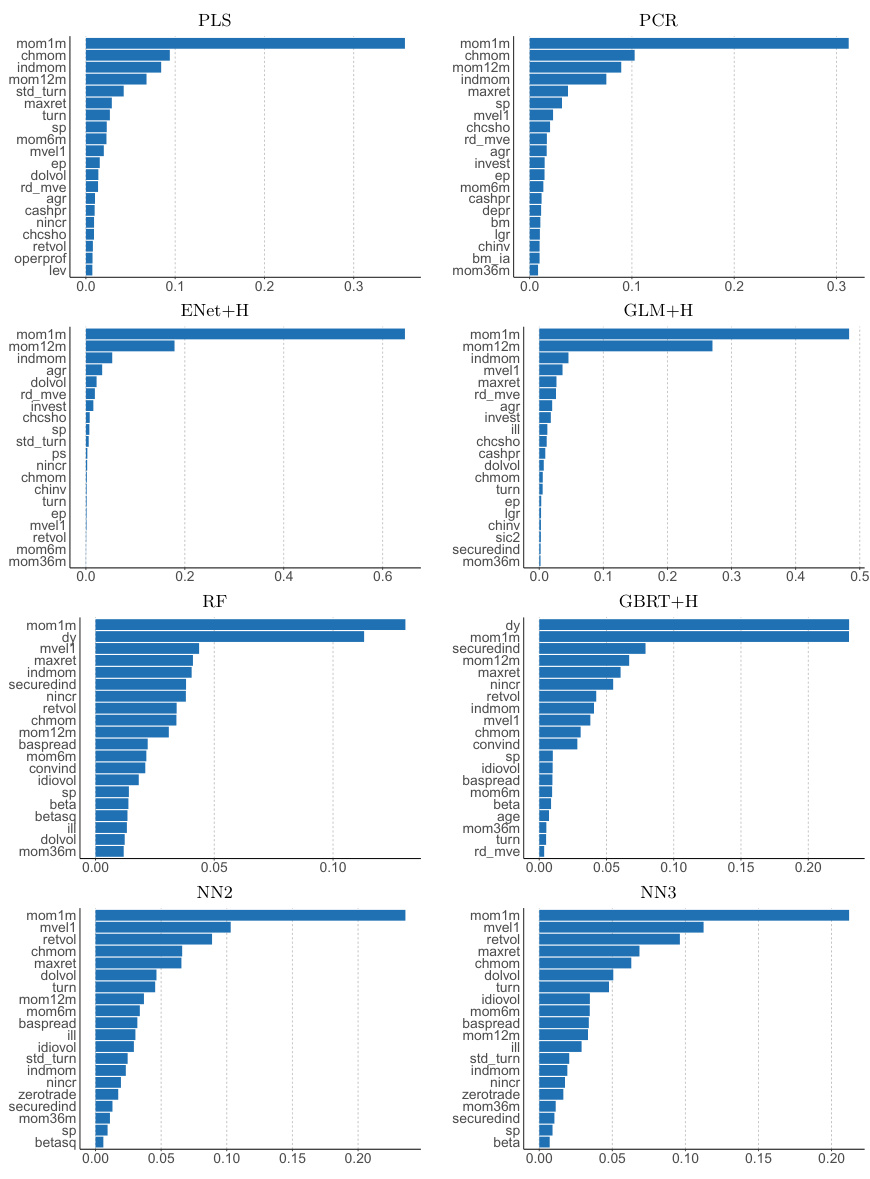
图5 94个特征统一排名（页33）

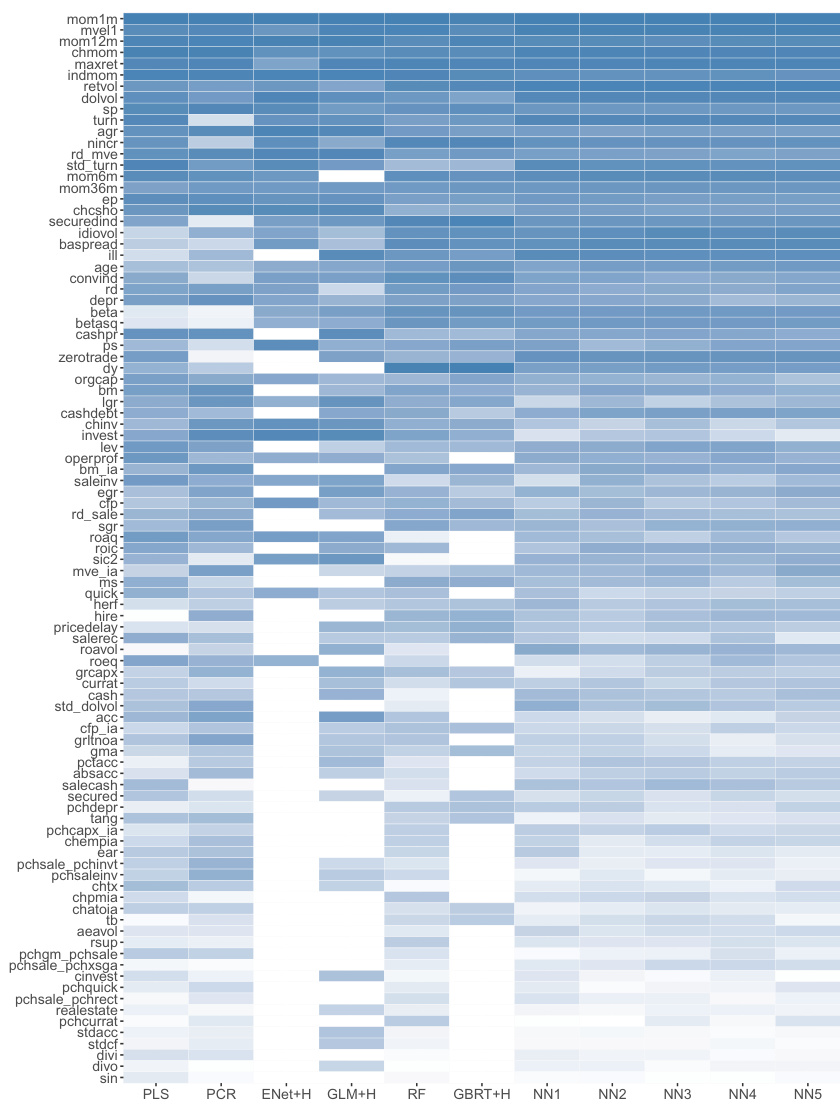
图6 边际效应示意（页36）

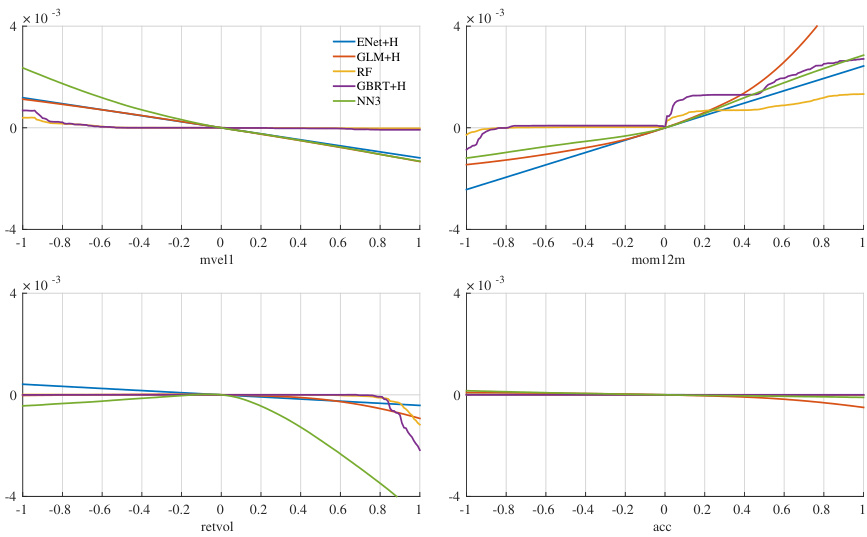
图7 神经网络中个股特征交互效应（页37）

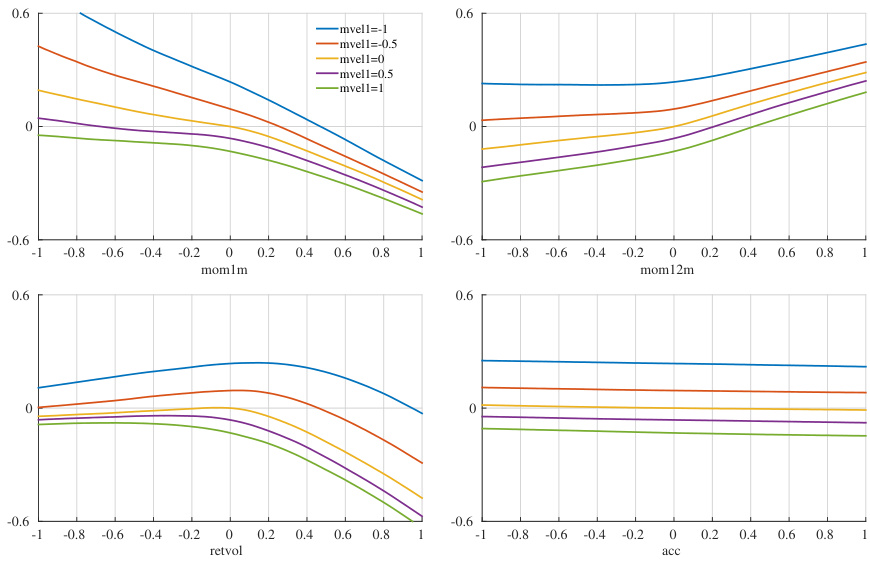
图8 股价特征与宏观交互（页37）

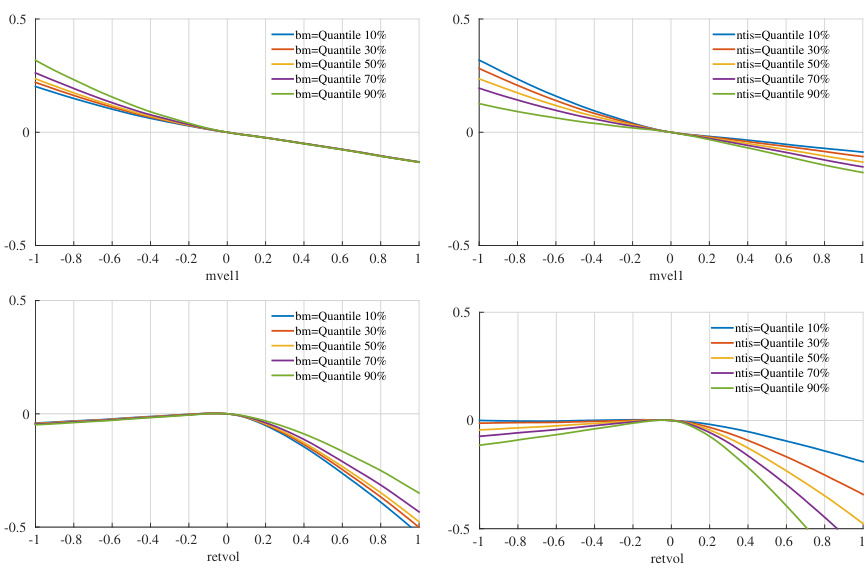
图9 机器学习投资组合收益累积（页46）

---

本报告详尽揭示了该篇机器学习在实证资产定价中的综合实力、方法差异、重要变量和经济效应，为学术研究和实际投资提供了宝贵的前沿视角和实证支持。

报告