彩票正向期望收益的数学建模与计算 [page::0][page::8][page::9]

• 通过参数模型$(f,F,t)$和绘画相关变量$(N,J)$建立数学模型，计算期望收益和中奖概率。

- 主要公式为预期收益(eRoR)：$$ eRoR=-f+\sumi ri (1-(1-pi)^N) + J s(1/t, N) $$

• 发现小规模销售且奖金超阈值的彩票开奖具有正期望收益，举例Lotto Texas达到正收益，Mega Millions和Powerball历史开奖均为负收益。

- 表格示例：

| 日期 | 彩票类型 | 奖金(J) | 销售量(N) | 期望收益(eRoR) |
|------------|--------------|-----------|------------|----------------|
| 2007/4/7 | Lotto Texas | 33.8m | 4.2m | +30% |
| 2007/3/6 | Mega Millions| 175m | 212m | -26% |
| 2006/2/18 | Powerball | 133m | 157m | -26% |

断点及边界判断：中奖销售比的关键作用 [page::13][page::16]

• 通过定义归一化变量$x=N/J$和$y=J/J0$，绘制断点曲线，正收益区域受限于销售与奖金比例的范围。

- Mega Millions和Powerball属于大销售量类别，几乎无正期望回报。

• 数学定理保证：当绘点落于曲线上方为正收益，落于曲线下方则是负收益。

彩票投资风险与投资组合分析 [page::23][page::26][page::27]

• 运用均值-方差组合理论分析彩票作为投资品的风险收益权衡。

- 设定包含传统股票指数、债券和房地产等资产的组合，引入彩票作为第六类资产。

• 彩票投资的方差巨大，即使存在正期望收益，也因极高风险导致理性投资组合分配极有限。

- 对于单次彩票，所需购买数以降低风险阈值极高(约14.5万张)，常规购彩规模难以进入组合。

• 负面结论：除非规模极大集合买票，否则不建议理性投资者买入彩票。

彩票投资建议与策略总结 [page::29]

• 避免Mega Millions和Powerball，优先考虑小销售量且奖金超过中奖门槛的彩票。

- 若期望收益为正，可通过购买彩票全套（Buyout）获得更高收益，但成本高且涉及法律及操作风险。

• 彩票为赌博消遣产品而非理性投资品。

- 建议理性投资者关注传统金融资产组合，彩票可视为极小额娱乐性持有。

找出彩票中的好赌注及为何你不应下注——详尽分析报告

---

1. 元数据与概览

标题：「Finding good bets in the lottery, and why you shouldn’t take them」
作者：Aaron Abrams 和 Skip Garibaldi
发布时间：报告截止到2008年数据撰写，具体发表时间不详，最新引用为2008年底。
主题：彩票投资分析，聚焦美国主要的彩票游戏（Mega Millions、Powerball及地方彩票如Lotto Texas和New Jersey Pick 6），金融数学与经济学视角下彩票投资的收益及风险研究。

核心论点：

• 传统认为彩票投注是“坏投资”，原因是彩票运营者盈利模式必然导致期望收益为负。

- 然而，对滚动累积奖金彩票（如Mega Millions和Powerball）进行深入数学建模，发现某些彩票期数存在正的预期回报率（eRoR），即存在“好赌注”。

• 正期望回报的赌注并不代表是“好投资”，投资决策还需考虑风险。

- 结合数学和经济理论（投资组合理论），即使在预期收益为正的情况下，彩票的高风险使其在理性投资组合中所占比重极小。

• 特别指出Mega Millions和Powerball因参与人数（票数）大，尽管奖金巨大，实际期望收益始终为负。

- 引导读者如何利用数学模型甄别什么样的彩票期数可能存在正期望收益，以及为何这些期数通常不构成理想投资机会。

综上，报告强调了区分“好赌注”（数学期望收益正）、“好投资”（风险加权回报）和“好主意”（非财务角度的娱乐价值）的重要性。同时报告用数学模型、统计数据和经济理论系统阐释不应轻易购买彩票的根本原因。[page::0, page::1, page::2]

---

2. 逐节深度解读

2.1 引言与问题提出（第0–2页）

• 彩票为何是“坏投资”传统解释是彩票本质上是庄家赚钱的游戏，支付给玩家的奖金低于总下注额。

- 滚动头奖彩票如Mega Millions、Powerball所累积的巨奖会导致某些期次单注彩票的预期收益可能为正 - 这提出“好赌注是否等于好投资”的问题。

• 研究问题聚焦于：（1）如何判定某期彩票是否“好赌注”，（2）当彩票期望收益为正时，是否应购买彩票，是否“值得投入”从投资角度看。[page::0, page::1, page::2]

2.2 彩票建模与参数设定（第3–7页）

• 通过分析具体游戏规则建立统一模型。区分固定奖金、按销量分奖金（pari-mutuel）和股票奖池（奖池型）三类奖金。

- 彩票结构参数包括：总票数$t$，固定奖项数量和金额$ai$，分奖金占比分配比例$ri$，总销量$N$，头奖奖池金额$J$。

• 考虑税收，采用扣除25%联邦税后的奖金金额，简化模型的同时较为现实。

- 表格1详细列出Mega Millions与Powerball不同中奖组合的奖金及对应配对方式，表3a列举具体历史大奖的年金总额、一次性奖金及其税后现值估算，表3b基于彩票结构参数计算关键统计量$f,F,J0$，其中$J0=F t$称为“头奖门槛”。[page::3, page::4, page::6, page::7, page::8]

2.3 预期收益率（eRoR）计算模型与性质（第8–13页）

• 制定数学表达式计算预期收益率，包括固定奖金、分奖金和头奖部分。最关键函数$s(p,N)$用于刻画中奖者分享奖金时的收益概率分布。

- 利用二项分布模型实现精确计算，给出闭式表达形式$s(p,N)=\frac{1-(1-p)^N}{N}$。

• 结合定义参数，使用公式(4.5)列出期望收益率计算方法。

- 计算历史大奖期次实际eRoR，表4显示某一Lotto Texas大奖具有+30%正收益率，Mega Millions和Powerball对应大奖显示负收益（-26%至-31%）。

• 通过数学证明，期望收益率必须满足$J>J0=F t$门槛才能有正收益，实现排除绝大多数低奖金期。（即若奖池$J$小于$J0$，则必定为“坏赌注”）。

- 这里$J0$成为判定“正收益”期次的关键统计门槛。该结论以多组现实数据验证，极大简化实际判别过程。[page::8, page::9, page::12, page::13]

2.4 预期收益率的分界曲线与彩票类型（第14–20页）

• 提出标准化变量$x=N/J$（销量与奖金之比），$y=J/J0$（奖金相对门槛比例），分析eRoR零水平线（break-even curve）在$(x,y)$平面的分布。

- 推导定理（Theorem 6.5）指出：
- 若销量相对奖金较小（$x<0.2$）且奖金显著大于门槛（$y>1.4$），出现“好赌注”的概率较大。
- 若销量相对奖金偏大（$x>1.12$）且奖金不超过两倍门槛（$y<2$），则eRoR始终为负，不能构成好赌注。

• 结合历史数据及标准值，Mega Millions和Powerball均属于销量大于奖金比例的类型，符合后者情况，即无正收益赌注。

- 小彩票类型如Lotto Texas可能存在良好投注机会。

• 图6a和6b清晰可视化上述理论结果，实际数据点与分界线对应良好，印证理论。

- 图7则解释相关区域界定，明确什么参数组合下可认为存在好赌注。[page::14, page::15, page::16, page::17, page::18, page::19, page::20]

2.5 Mega Millions与Powerball未来走势预测（第21–22页）

• 基于之前的分析，Mega Millions和Powerball由于参与人数众多，几乎无可能在未来形成正期望收益的下注机会。

- 计算了奖池滚存增长与奖池增长次数的概率模型，显示奖池要达到倍增的门槛极为罕见，大约22年会出现一次（远长于彩票运营周期）。

• 通过概率界定及历史趋势，合理推断未来Mega Millions、Powerball无积极投资价值。

- 即使偶尔达到理论上的正期望收益，也因高风险和不确定性不宜投注，也提醒仍需多考虑是否为好投资，而非仅看好赌注。[[page::21, page::22]

2.6 投资与风险分析引入（第23–24页）

• 即便存在正期望赌注，是否为“好投资”依赖于风险权衡。

- 介绍马科维茨均值-方差投资组合理论（mean-variance portfolio theory）， 理性的投资者不仅关注预期回报，还关注方差（风险）。

• 强调偏好假设及经济学逻辑：投资者风险厌恶，若两个方案期望相同则倾向风险较低方案。

- 以金融市场典型标的（国债、股票指数等）构建投资组合为例，阐述如何权衡各种资产收益率与风险。[page::23,page::24]

2.7 金融资产组合实证与计算（第25页）

• 利用1972-2007年股票市场数据（包括债券基金、MSCI国际指数、房产信托、标准普尔500、纳斯达克），计算年化预期收益率及协方差矩阵。

- 提出投资组合权重计算方法，考虑动用风险资产投资组合与无风险资产配置的分离定理。

• 给出最优投资组合权重的数学表达式与具体数据系数。为后续加入彩票资产做准备。[page::25]

2.8 彩票资产纳入组合分析及风险估算（第26–28页）

• 将具体彩票期次视为单一资产，标明预期收益率和分散度（方差）。

- 估算彩票资产的方差以反映中奖金额分布及分奖情况，特别是考虑多人共享头奖的复杂性。计算显示彩票的收益方差极高（可达10^11数量级）。

• 假设投资人通过买票联合体（Syndicate）购入彩票，投资者自己份额对应购票份数，投资方差随购票数线性递减。

- 引入“否定定理”（Negative Theorem）：若彩票资产的方差过大，投资组合中彩票权重极小，不构成合理投资，即使预期收益较高。

• 实例说明，若购票规模不足约14.5万张（例如小型投资者），根据方差阈值无法有效配置彩票资产，彩票在实际投资组合中被忽略。

- 证明基于投资组合理论的权重计算逻辑和投资者风险偏好假设。[page::26, page::27, page::28]

2.9 结论（第29–30页）

• 如何赚钱：

- 仅想期望赚取正收益，应关注小销量高奖池的彩票，如Lotto Texas之类，且奖池必须超过门槛$J0$以上。
- Mega Millions和Powerball不属于此类，应避免参与。

• 买断策略：通过购买全套彩票（buyout）可获得稳定期望正收益，但操作难度大、正因投资数额巨大，且面临法律和交易实际问题。历史上有成功案例但伴公网阻力，需谨慎。

- 投资建议：结合风险收益权衡分析常规彩票非理想投资，购票联合体可能因规模效应小规模投资者参与价值有限。

• 其他策略：提出设想运营改良型彩票或类似游戏以提升玩家收益率，尽管现实法律限制严格。

总体结论是，数学模型展示彩票中存在正期望的赌注，但经济投资角度风险过高导致彩票不是理想投资工具。[page::29, page::30]

---

3. 图表深度解读

表1（第4页）

描述：Mega Millions和Powerball各中奖类别对应奖金金额和组合数量。

• 赛制细分为5/5+额外、5/5、4/5+额外等各等级，奖金金额由头奖至最低奖励2美元。

- 中奖方式数量开列，体现中奖概率大小。
解读：展示各奖项概率及奖金结构，基础数据支持后续期望收益计算。表中已扣除税后额，现实更接近玩家实际收益。
联系文本：明确游戏规则参数与奖金数据，是模型参数$f,F$计算基础。[page::4]

表3a（第7页）

描述：对抽取历史特定日期大奖（Lotto Texas、Mega Millions、Powerball）年金和一次性奖金（税前）及$J$（税后现值）估算。
解读：表明头奖价值减税后实际数额，$J$远小于公布头奖金额的25%左右，为数学模型参照的核心奖金变量。对应计算案例中的获奖金额。
联系文本：$J$成为期望收益计算的关键变量，且定义为税后现值，避免复杂税务问题。[page::7]

表3b（第8页）

描述：参数$t,f,F,J0$统计值，基于彩票结构固定而非具体期次。

• $t$为所有可能号码组合数。

- $f$为扣除固定奖金期望的票价部分比例。

• $F$扣除分奖金部分，如利润与彩票管理费占比。

- $J0=F t$定义为“奖池门槛”。
解读：Mega Millions和Powerball$J0$均超过百亿美元的门槛，表明必须达到此金额彩票才可能有正期望回报。
联系文本：数学定理中以此评价彩票正负期望收益区分的关键门槛。[page::8]

表4（第9页）

描述：几个样本彩票期次重要参数$J,N$及其预期收益率及相关比率。
解读：Lotto Texas大奖展示30%正期望收益率，而Mega Millions和Powerball扣税后奖金巨大，均无正期望。
联系文本：佐证结论中流行彩票因销量大而无正期望收益；小型彩票如Lotto Texas可出现正期望。[page::9]

图6a（第16页）

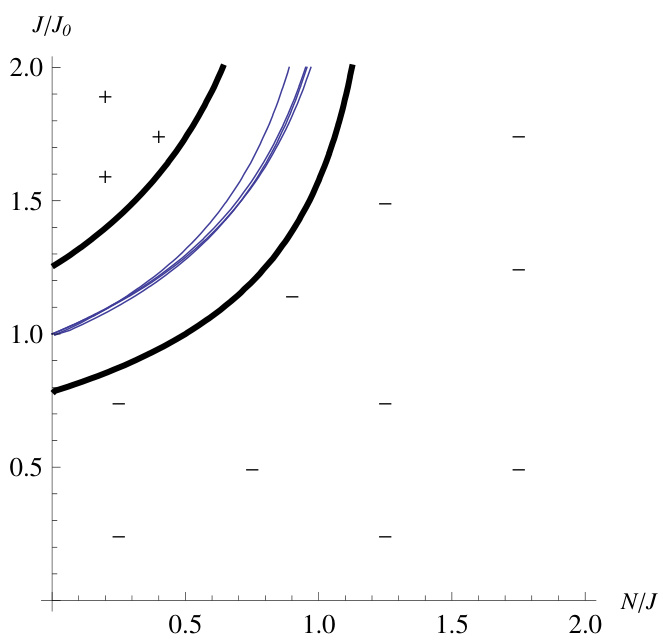
描述：基于$x=N/J$与$y=J/J0$标准化变量绘制的eRoR零水平线（break-even curves），黑色粗线代表一般边界，浅蓝色曲线为四种彩票的实际边界。
解读：展示区域划分，曲线左上方为正预期收益区域，右下为负收益区。Mega Millions和Powerball实际边界靠近低收益区。
联系文本：直观显示典型彩票类型eRoR的边界，验证理论6.5定理。[page::16]

图6b（第19页）

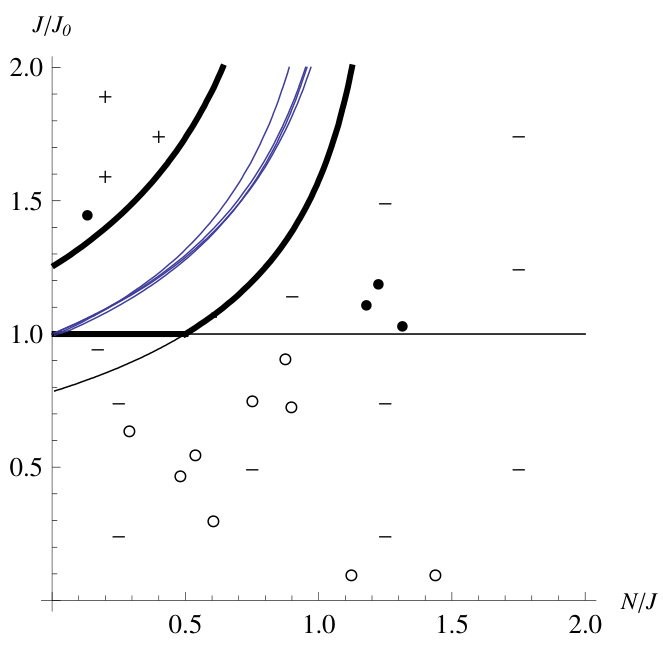
描述：图6a的细化及实际历史数据点标注（实心点、空心点等）。
解读：实际历史期次集聚于负收益区域，只有少数接近或落入正收益区的小型彩票期数。
联系文本：具体展示历史数据验证理论界限及彩票市场实际波动范围。
[page::19]

图7（第20页）

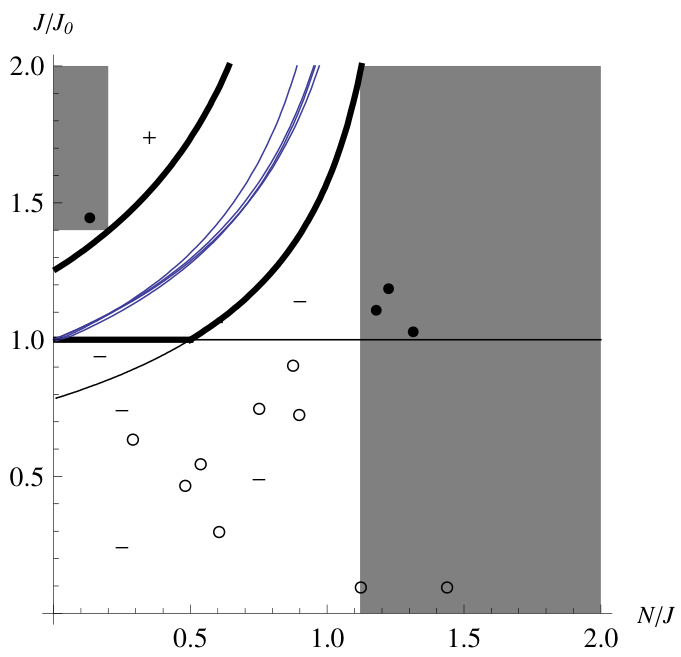
描述：区分小销量正收益区（左上阴影）与大销量负收益区（右阴影），历史数据点叠加。
解读：明确了小玩法与大奖门槛满足时属于好赌注区域，而大玩法如Mega Millions则连年处于负步区。
联系文本：是理解彩票结构决定投资价值的形象工具。[page::20]

表10（第26页）

描述：五种典型风险资产的周收益率、预期收益率及收益率方差协方差矩阵。
解读：为后续投资组合计算提供标准对照，金融市场资产的统计属性用于在引入彩票资产后比较权重分配。
联系文本：为阐释彩票理性投资比例提供参考矩阵，建立数学基础。[page::26]

---

4. 估值分析（投资组合理论）

本报告估值部分以“期限固定的预期收益率”和“收益率波动率（方差）”为核心指标，选取了现代投资组合理论基础——马科维茨均值-方差组合理论。

• 方法：

- 投资者基于期望收益和风险（收益率方差）进行资产配置，风险偏好体现在风险厌恶参数体现。
- 考虑无风险收益率$RF$和多种风险资产，通过线性代数计算最优投资权重向量$X=C^{-1}(\mu - RF \mathbf{1})$，其中$\mu$为风险资产收益率向量，$C$为协方差矩阵。
- 票务资产被嵌入模型作为第六资产，添加相关期望收益$RL$和估计方差$v$。

• 关键假设：

- 投资者关注的唯一指标为预期收益、收益方差和资产间的协方差（无偏好意外因素）。
- 投资比例合计为1，支持有限度做空（Lintnerian短卖限制）。
- 方差远大于预期收益平方，即波动性极大。

• 结论：

- 由于彩票资产方差极高，即使彩票资产期望收益高于风险资产，投资组合中其权重$\hat{X}6$很可能极小。
- 货币量小的普通投资者若投资彩票，投资比例几乎为零；只有在极大规模购票（例如联合购票模式），方差被稀释后才可能提出合理配置。

• 否定定理（Negative Theorem）：

- 设定阈值$\theta$为投资比例的下限，当彩票投资方差$v$大于$\frac{RL - RF}{0.022 \theta}$时，最优组合中彩票权重低于$\theta$，即占比可忽略。
- 结合实测Lotto Texas案例，计算显示若投资者购票低于约14.5万张，则彩票投资被完全否定。

该估值与风险分析与此前的预期收益理论紧密结合，凸显彩票作为投资标的的高风险特征严重限制了理性投资分配。[page::24, page::25, page::26, page::27, page::28]

---

5. 风险因素评估

报告主要识别的风险包括：

• 高风险方差：即使预期收益正值，彩票收益不确定性极大，可能导致巨大亏损。

- 奖池滚存概率不足：彩票能否达到使单注期望值为正的头奖规模，存在概率限制，难以长期实现。

• 税务因素：中头奖后扣税影响显著，减少实际收益。

- 法律风险：如买断全套票面临官方阻挠和法律纠纷。

• 市场饱和风险：奖池无限滚大假设不现实，市场容量有限。

- 行为风险：大多数玩家随性选择非均匀号码，虽可提高单注回报率但影响有限。

报告未详述直接风险缓解策略，但利用数学预判、严格限制购票规模以及非投资角度娱乐心态被视为“风险控制”。同时报告以经济理论对比风险收益权衡为基础，否定了长期投资基于彩票的可能性。[page::22, page::29]

---

6. 批判性视角与细微差别

• 模型假设限制：模型假设其他玩家随机选号，忽略非随机选号和号码冷热门效应，实际策略可略微提高预期收益，但不会改变风险结构。

- 税务处理简化：只考虑联邦税避免复杂性，但忽略州税可能对部分地区产生小影响。

• 彩票结构简化：忽视部分彩票多层投注及增额赠奖选项，可能对部分结果有偏差。

- 投资者风险偏好统一假设：报告仅用均值-方差理论，忽视行为金融学因素。

• 数据时效性：历史数据截至2008年，彩票规则及奖金实际水平可能变动，需保持时刻更新。

- 法律风险未量化：对买断及高频大额投注可能产生的执法干预给出简短描述，缺乏深入法律分析。

报告立场严谨且数据详实，但上述限制点建议读者认知潜在误差边界。[page::4, page::10, page::22, page::29]

---

7. 结论性综合

该报告从彩票的数学概率模型入手，将固定奖金、分奖金及头奖组成彩票期望收益精确公式，抽象出彩票类型参数$f,F,J0$，并定义赔率收益函数$s(p,N)$。基于大量历史数据，建立了“中奖金额至少超过门槛$J_0$才可能有正期望收益”的有效判别法则，同时引入销量与奖金比例$x=N/J$作为重要指数。

通过绘制破产临界曲线（break-even curve），明确划分彩票类型可形成好赌注的数学区域，其中低销量高奖池的彩票更有可能正期望收益。报告尤为指出：

• Mega Millions和Powerball长期以来及预测未来极难出现正期望投注机会，因销售规模大大超过奖池一般倍数，符合大销量负期望的数学规律。

- 小彩票如Lotto Texas存在正期望投注，历史数据验证其正收益的可能性和偶发性。

• 彩票虽然时有正期望，基于投资组合理论计算体现的高波动率使彩票在理性优化投资组合中所占权重极微，不适合作为主流投资标的。

- 购票联合体凭借规模化购票以降低风险方差，可能改变投资组合态势，但普通投资者难以承担。

• 买断全套彩票策略在实际操作中成本高企、法律障碍多且执行复杂，非普适投资方式。

图表部分深刻展示彩票参数与收益率关系，清晰确认了理论与现实数据的一致性，例如破产曲线的边界包络与真实历史期次数据准确对位，为彩票投资价值提供了科学判断标准。

综上，报告的核心是在强调区分数学上的“好赌注”和经济学投资中的良好风控之间的区别，引导公众理性认知彩票投资的风险与收益，揭示平凡投资者依据期望收益盲目购买彩票的风险实质。

---
（全文引文均已在报告页码相应标注）

报告