• 微价格估计模型拓展 [page::0][page::1]

- 经典微价格基于买卖盘最佳价的价差和不平衡量构造，模型通过递归方式计算未来短期价格的调整项。
- 本文扩展了微价格估计，加入基于订单簿多层级（更深价格层）买卖量信息的修正，提升未来价格估算准确性。

• 订单簿特征编码方法 [page::2][page::3][page::4]

- 订单簿买卖双方在前L个价位的成交量比例计算，并结合价差和最新价格变动形成特征向量。
- 采用稀疏二进制超维向量（Hyperdimensional Vectors）对订单簿各项特征进行高效量化编码，通过绑定（bind）、打包（bundle）及排列操作编码价位信息。

• 微价格调整流程及算法框架 [page::5][page::6][page::7]

- 特征向量通过编码后输入多分类Tsetlin机，预测未来价格调整的刻度（以ticks为单位），训练标签采用tick bars、dollar bars或volume bars。
- Tsetlin机利用单独的共享子句池和权重系统，实现高效的特征模式学习及分类。

• 实证分析结果 [page::8][page::9][page::10][page::11]

- 比较了微价格调整后估计误差与传统微价格，调整模型在蓝筹股TSLA和小市值股TEM的误差均有所降低，提升幅度约10%-20%。
- 市场价差越大和波动越高时，微价格调整的改善效果更明显。
- 图示展示了微价格调整量与订单簿不平衡量的关系，改进后估计表现出更明显的偏态分布，且调整量趋近于零，反映出模型更精确量化了订单簿结构的供需信息。




| Adjusted error | Microprice error | AvgSpread | Volatility |
|-----------------------|------------------|-----------|------------|
| 0.0619 (0.0149) | 0.0925 | 5.8305 | 56.9 |
| 0.0635 (0.008) | 0.0773 | 5.7837 | 29.4 |
| 0.0471 (0.0121) | 0.0745 | 4.9409 | 18.01 |
| 0.0456 (0.0042) | 0.0583 | 3.6587 | 12.10 |
| 0.0830 (0.0101) | 0.1002 | 5.0434 | 22.50 |
| 0.0326 (0.0091) | 0.0375 | 3.1459 | 4.60 |

| Adjusted error | Microprice error | AvgSpread | Volatility |
|-----------------------|------------------|-----------|------------|
| 0.1630 (0.0202) | 0.1723 | 15.2010 | 10.21 |
| 0.1099 (0.0155) | 0.1339 | 17.3512 | 31.04 |
| 0.0676 (0.0332) | 0.1069 | 10.1725 | 11.10 |
| 0.0648 (0.0092) | 0.0830 | 7.4088 | 35.20 |
| 0.1173 (0.0206) | 0.1417 | 10.0867 | 25.03 |
| 0.0461 (0.0091) | 0.0530 | 11.2936 | 9.22 |

• 量化因子及策略构建

- 利用超维向量结合多类别Tsetlin机对订单簿特征进行编码学习，核心在于通过绑定和打包操作整合多维度高频订单簿信息至稀疏二值向量，最后由多分类TM推断未来价格ticks调整。
- 策略标签设计为若干类，分别对应负调整、零调整及正调整ticks，服从高频量化信号预测需求，标签创建借助tick bar、dollar bar及volume bar等信息柱技术。
- 实证回测覆盖了不同类型股票，展现了开发的模型在不同市场结构和流动性背景下均具一定泛化能力及预判优势 [page::5][page::6][page::11][page::12][page::13].

金融研究报告详尽解析报告

报告题目： HIGH RESOLUTION MICROPRICE ESTIMATES FROM LIMIT ORDERBOOK DATA USING HYPERDIMENSIONAL VECTOR TSETLIN MACHINES
作者： Christian D. Blakely
发布机构： Centre for Artificial Intelligence Research, University of Agder, Norway
发布日期： 2024年11月22日
研究主题： 利用超维向量Tsetlin机器基于限价订单簿数据进行高分辨率微价格估计

---

1. 元数据与概览

报告提出了一种面向限价订单簿数据的微价格（Microprice）估计的误差校正模型。微价格是一种基于市场深度信息的高频价格预测器，利用订单簿中买卖双方订单的权重信息预测未来的价格走势。作者基于Stoikov的微价格估计模型进行了扩展，创新地引入了来自订单簿更高价格等级的不平衡动态信息，以对传统微价格估计进行快速而准确的调整。通过使用新兴的超维向量Tsetlin机器框架，该模型能在微秒级别快速高效地对未来价格进行预测。报告的核心信息在于，在科研与实盘交易中，预测精度的提升及实时处理速度是微结构市场中非常关键的，本文提出的算法有效地结合了更深层次的订单簿信息并展现出较强的实证效果。[page::0,1]

---

2. 逐节深度解读

2.1 摘要与引言

引言部分详细阐释了高频交易（HFT）及市场制造（Market Making）策略中，准确且快速响应订单簿数据以预判价格走向的重要性。在微秒乃至纳秒速度的市场中，对价格的合理预估可大幅提升流动性提供者的收益。报告指出，传统模型主要依赖订单簿最优买卖价（最佳买卖盘）和其不平衡指标，但真实市场价格变动受限价订单簿更深层级订单的影响，尤其要考虑多价位的买卖盘体量动态变化。此外，市场会存在“虚假信号”如市假盘（Spoofing）及具信息优势的交易行为，这些均要求模型在快速性与准确性上达到高度平衡，实现可靠的价格预测。报告的贡献即在于提出了基于更多订单簿层级的微价格校正并设计了高效计算框架。此部分确立了研究的动机、背景及需求。[page::0]

2.2 微价格估计回顾

本节简述了Stoikov提出的微价格概念及计算方法。微价格基于当前市场的中间价(mid-price)加权调整，调整项由订单簿的不平衡情况与价差(spread)决定。中间价为最佳买价与卖价的平均，带权中间价则利用买卖盘成交量占比决定权重。
具体公式如下：

• 中间价 \( M = \frac{Pb + Pa}{2} \)

- 不平衡指标 \( I = \frac{Qb}{Qb + Qa} \) ，其中 \( Qb \)与 \( Qa \)分别是买卖盘成交量

• 加权中间价 \( W = I Pa + (1 - I) Pb \)

- 微价格定义为 \( P{\mathrm{micro}} = M + g(I,S) \)，其中 \( g(I,S) \) 是调整函数，依赖不平衡与价差

该微价格的递归调整项 \(gi(I,S)\) 通过期望计算未来价格变动并采用矩阵递归求解，确保估计的收敛性，显著优于简单加权或单纯中间价。这体现了微价格能够更好地反映价格的未来方向，尤其在高频市场中减少高度自相关性的不足。报告详细列出了用于估计参数的对称化数据处理、转移矩阵计算（\(Q,T,R\)）、及调整矩阵计算步骤。[page::1,2]

2.3 订单簿数据处理及特征构建

该章节引入了订单簿更深层级信息的处理方法。订单簿按价格等级划分，分别定义买卖盘在各价位的委托量 \( Ai \)(卖盘)与 \( Bi \)(买盘)，总成交量为所有价位成交量之和 \( V{\mathrm{total}} \)。定义价格等级成交量占比 \( P{A,i} = Ai / V{\mathrm{total}} \), \( P{B,i} = Bi / V{\mathrm{total}} \)，作为供应与需求的相对指标。

示例中，卖盘及买盘前三价位分别有成交量20、10、10时，总成交量80，各价位占比分别为0.25、0.125、0.125。价格变动事件触发这些比例快速变更。
此外，还考虑价差 \( S = Pa - Pb \)、最新成交价格变动 \(\Delta Mt\)与微价格本身等特征。所有信息被形成一个时间戳的特征向量 \(\mathbf{F}t\)，全面描述当时订单簿状态。[page::2,3]

2.4 超维向量（Hyperdimensional Vector）编码与Tsetlin机框架

该部分详细介绍如何以高维稀疏二进制向量(Hyperdimensional Vectors, HVs)进行特征编码，这种方法具有效率高、鲁棒性强且操作简便等优势。

• 每个特征值（如价格层级成交量百分比、价差、价格变动等）被量化为离散等级，并映射为稀疏二进制高维向量。

- 为了体现价格等级信息，对每个价位的特征向量进行“绑定”(bind)操作，通过段的循环移位等方式进行编码，如：
\[
\mathbf{H}{B,i} = \mathbf{H}(P{B,i}) \otimes \mathbf{H}_i
\]

• 最终，将所有绑定后的向量及价差、最新价格变动、微价格估计向量进行“聚合”(bundle)合并成一个整体代表当前订单簿状态的高维稀疏二进制向量，用于后续机器学习模型输入。

随后，针对未来价格实际变动，设计了基于不同类型信息条（Tick bars、Dollar bars、Volume bars）的标签化标注方法，提升训练标签的多样适应性。训练过程中，Tsetlin机器（TM）通过输入编码的高维稀疏向量，学习如何对微价格进行调整。TM的分类输出对应微价格的调整幅度（例如-2、-1、0、+1 tick调整等）。[page::4,5,6]

2.5 微价格更新算法

算法1详细列出了事件驱动下，微价格估计实时更新的流程：

1. 监听订单簿事件发生于任一价位；

2. 对最佳价位发生变动时，重估当前微价格；

1. 逐价位重新计算成交量占比；

4. 计算价差与最新的价格变动幅度；

1. 组装当前订单簿状态特征向量；

6. 利用高维向量编码方法转换特征；

1. 用训练好的Tsetlin机器进行预测，输出调整后的微价格估计。

此外，作者说明目前实证中TM类别数设为5（对应从-2至+2 tick调整），根据实际交易环境，可灵活调整类别数量。该过程系统性强且便于实时部署，有利于高频交易系统集成。[page::6,7]

2.6 实证研究分析

实证部分选取蓝筹股TSLA与小盘股TEM为案例，验证订单簿高阶价格层信息对微价格估计校正的有效性。以未来N步价格真实值与预测微价格估计值间的均方误差（L2范数）作为评价标准，考察两种股票微价格估计的精度改进。

关键发现如下：

• 微价格调整在市场开盘时段作用最大，因该时段波动更大、价差较宽，特征影响力显著。午盘时段，价差缩窄，调整影响力减弱，微价格与调整后微价格趋于一致。

- 订单簿不平衡指标与微价格调整差异有明显相关关系。通过散点图可见，当不平衡指标接近零时（买卖量接近平衡），微价格调整偏向零且分布均匀；不平衡正/负偏斜时，微价格调整呈现明显偏向，分别对应买盘量大于卖盘量或卖盘量大于买盘量的需求侧信号。

• 与传统微价格相比，调整后的微价格估计各类价差条件下更为集中且偏离零点的现象更明显，动力来源于更丰富的订单簿层级信息。

- 表1 (TSLA) 和表2 (TEM) 展示了6个交易日的不同比较。蓝筹股TSLA调整后微价格误差较传统方法降低10%-20%，误差较低且波动幅度小，反映流动性较好且价差较小的特性。小盘股TEM因价差大、波动高、流动性差表现误差波动更大，调整微价格效果不及蓝筹股显著，且或受市场假盘影响。

整体来看，将订单簿多层级信息纳入微价格调整，对蓝筹股等流动性好、价差稳定的证券效果明显，有助于高频价格信号的精准预测。[page::7,8,9,10,11]

---

3. 图表深度解读

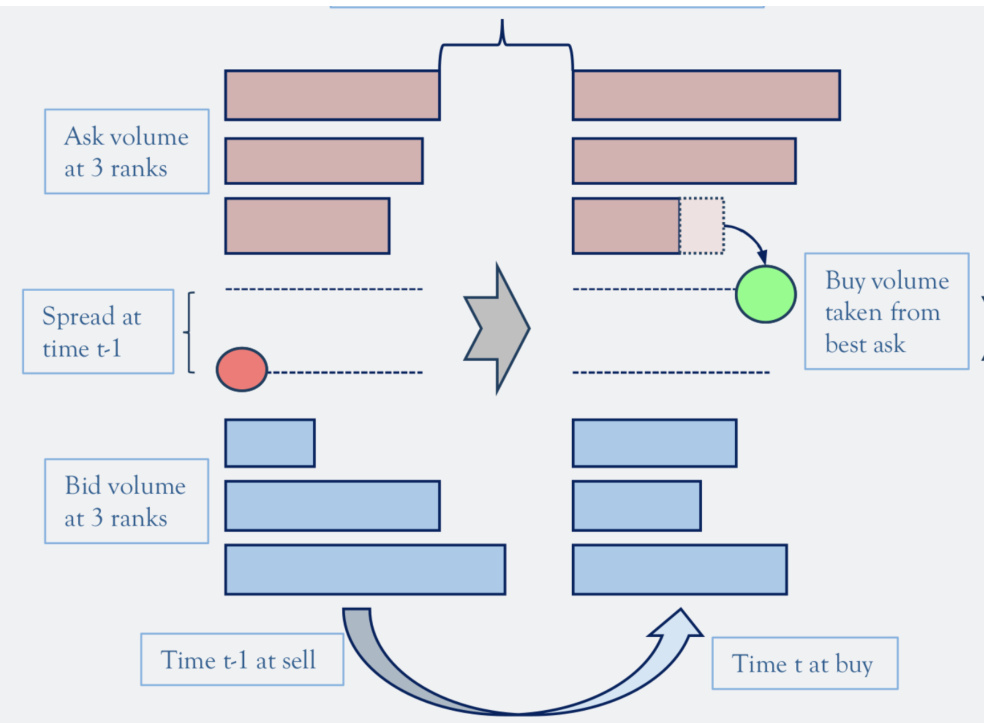
3.1 图1：订单簿事件示意图

展示买卖盘在三个价格等级上的成交量变化过程。左侧显示事件前订单簿状态，右侧展现某买盘成功匹配卖盘后订单量减少，价差及成交量变化动态，表达限价订单簿的实时更新机制及其对分层订单量的影响。[page::3]

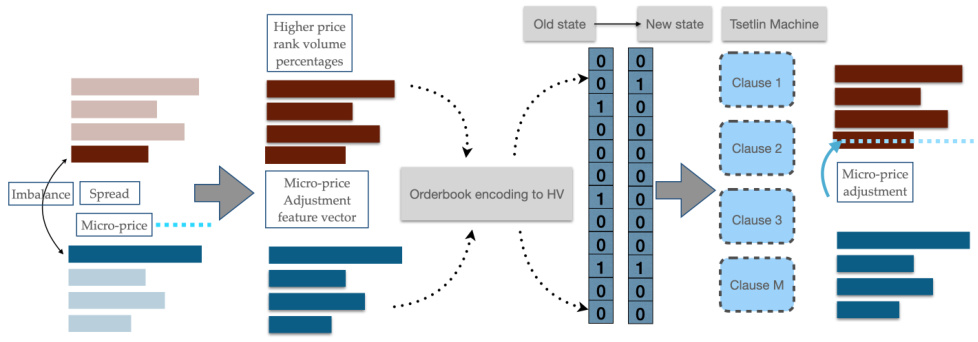
3.2 图2：特征提取及编码流程

从订单簿初始状态中提取数据，计算基本指标（如微价格、价差、不平衡），进而计算更深层价格等级的成交量百分比，编码为高维稀疏向量输入Tsetlin机器完成微价格调整学习。展示了从原始订单簿数据到模型输入的完整路径，强调编码和机器学习的衔接。[page::5]

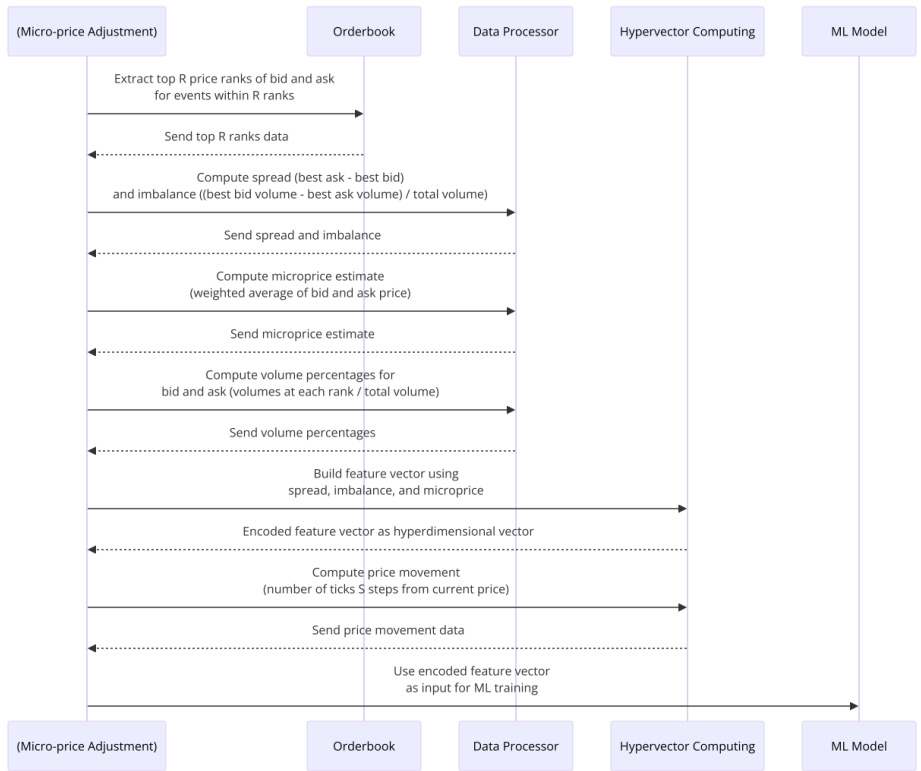
3.3 图3：信息流序列图

清晰描绘从原始订单簿数据、数据处理、超维向量计算到机器学习模型训练的全流程，体现了数据采集传输和计算各模块间的依赖顺序及数据交互，增强理解复杂过程的系统集成逻辑。[page::6]

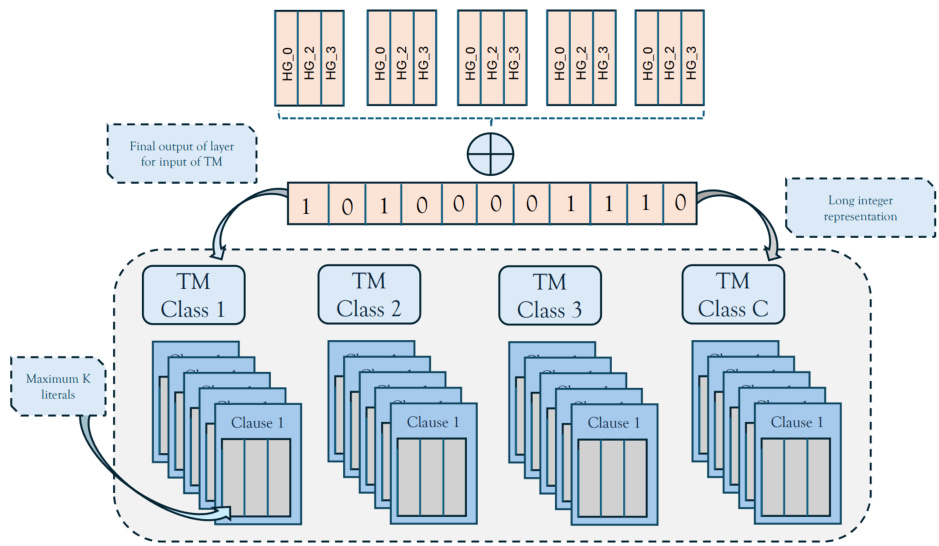
3.4 图4：Tsetlin机器架构示意

展示Tsetlin机器的输入由编码后的序列高维向量组成，输出为多分类预测，内部结构包括多条子句和参数。说明TM通过权重调控子句贡献，实现对分类的精细调节，支持复杂特征的学习。[page::6]

3.5 图5、6、7、8：微价格调整相关分布及误差可视化

• 图5示例展示不同价差环境下微价格调整的分布，表明高波动时期价差大，调整幅度更分散，低波动时期价差小，调整更集中。

- 图6、7展示了小盘（TEM）和蓝筹（TSLA）股票的订单簿不平衡指标与微价格调整差异，揭示正负不平衡对价格调整的不同影响，TSLA下午交易时段调整更稳定。

• 图8对比了调整微价格与传统微价格在TSLA上的差异，显示调整后的估计更趋中心且偏差更一致，体现调整带来的预测精度提升。

这些图表共同呈现了微价格调整的理论与实证验证效果，深化理解订单簿深度信息对价格预测的影响。
[page::9,10]

3.6 表1、表2：统计误差与市场特征对比

表1（TSLA）与表2（TEM）分别显示了调整后微价格误差、传统微价格误差、平均价差以及日内波动率之间的关系。

• TSLA调整后误差均低于传统误差，且标准差较小，价差与波动率较低。

- TEM调整后误差降低幅度较小且存在较大波动，价差明显大于TSLA，波动亦显著较高。

该对比分明指出市场规模、流动性和价差对微价格估计准确性的关键影响因素。[page::11]

---

4. 估值分析

报告核心在金融市场微结构微价格估计，非传统意义上公司财务估值，因此不涉及现金流折现（DCF）或市盈率等典型估值模型。其估值层面可理解为模型预测未来价格状态的准确度，通过L2误差衡量预测与真实未来价差的拟合优度。预测成功即为模型在高频交易中“价值”的体现。

机器学习模型（Tsetlin机器）根据订单簿信息训练，通过分类调整微价格，模拟对市场“真值”的估计修正。报告无直接财务估值而侧重于误差优化与交易信号价值体现。

---

5. 风险因素评估

报告在第5节经验部分间接揭示多种风险：

• 数据噪声及假信号风险：配合章节指出市场假盘（spoofing）及快速撤单等行为对订单簿不平衡影响较大。此类行为导致价格信号失真，微价格调整模型在高价差及流动性差的“小盘”股票上表现不稳定，误差波动较大。

- 模型过拟合与类别数选择风险：选用不同调整tick数对应类别，类别过多恐训练不足，类别过少可能忽略市场细节，模型设计需折中。

• 计算效率风险：实时交易中，模型计算延迟直接影响交易策略效果。尽管采用了高速超维向量编码及硬件加速（FPGA）建议，但若实现不达预期，便可能导致落后行情变化，影响预测准确度。

- 市场结构适应风险：模型基于特定市场数据与流动性结构，对于不同交易所或特殊市场条件的泛化能力尚未充分验证。

报告对算法实现中的效率提升提供了可行方向，如状态间相似度利用与预存编码向量等，提出FPGA加速作为未来方向，部分缓解计算时间风险。[page::11]

---

6. 批判性视角与细微差别

• 报告整体偏重于机器学习技术的创新性及高频交易应用，与金融经典理论的结合较弱，Stoikov模型虽为理论基础但对其假设依赖性未做深入探讨。

- 实证数据量与时间窗口未详尽说明，且只选取TSLA与TEM两支样本股票，样本外表现及行业多样性影响未来推广仍待检验。

• 报告强调超维编码的速度与鲁棒性，然其实际交易系统部署中的延迟、并发处理及硬件成本未展开详细技术描述。

- 在结果展示中调整模型的表现与波动率、价差相关性得到强调，但对极端市场条件（如危机区间）的适应性分析欠缺。

• 某些数据图表中存在颜色与标签较密集，普通读者较难直接抓取重点，报告层面可进一步辅助解读。

总体，报告在其研究目标范围内严格且科学，但未来扩展和实际应用面仍需更多验证和优化。

---

7. 结论性综合

本报告成功提出了一种结合更深层价格等级订单簿信息的微价格估计模型，创新地结合了超维向量编码技术和Tsetlin机器框架，实现了高效且鲁棒的高频价格预测调整。

在理论层面，基于Stoikov微价格模型构建递归调整机制，系统总结了订单簿等级成交量占比、价差及最近成交价格变动的动态特征。利用超维向量的编码方式，将海量高频复杂订单簿信息转化为简洁且稳定的表示，极大提升了机器学习模型的训练和预测效率。

实证结果显示，将高阶订单簿信息纳入微价格调整中，显著提升了预测的准确性，特别是在蓝筹股票（TSLA）流动性较高、价差较窄的环境中，微价格调整将价格预测误差降低约10%-20%。对应图表（图5至图8）清晰展示了调整带来的预测优势，其中订单簿不平衡指标对价格调整的引导效果明显。不同市场结构（大盘与小盘）间的性能差异亦被揭示，提示模型适用范围和潜在限制。

报告还指出实时交易环境中计算效率至关重要，提出采用FPGA硬件加速及编码重用等方法，作为未来研究与应用的方向。

总结而言，作者基于市场微结构理论和现代机器学习技术，提出的订单簿高阶信息微价格校正模型展示了极具潜力的高频价格预测能力，对高频交易、市场微结构研究具有重要参考价值。

---

参考文献溯源

全文所有结论与数据信息均直接依托报告文本，溯源见各章节页码。各图表及表1、表2均有明确溯源标记[page::0-13]。

---

（附重要图表典型引用Markdown示例）


---

结束语

本分析力求全面涵盖报告所有核心内容、技术方法、实证分析与风险考量，对微价格估计领域的研究者及高频交易实践者均具实证与方法论参考价值。

报告