期权定价模型基础及主流方法总结 [page::2][page::4][page::8]

• 资产价格遵循几何布朗运动，基于随机微分方程与伊藤引理建立标的资产价格模型。

- 树模型（包括单步、 多步和三叉树）适合美式期权定价，利用风险中性概率递推计算期权价格。

• 蒙特卡洛模拟通过生成大量价格路径，根据期权收益折现求均值，但收敛速度较慢。

- 有限差分法基于偏微分方程数值求解，包括显式、隐式和Crank-Nicolson三种类型，其中Crank-Nicolson兼顾稳定性和计算效率。

美式期权定价模型对比及参数优化 [page::11][page::12][page::13]

• 采用二叉树模型与有限差分法定价美式期权，有限差分法运行时间约0.0076秒，明显优于二叉树模型约0.2秒。

- 迭代的松弛因子ω取值(1,2)区间时，有限差分法结果与二叉树模型基本一致，误差最小。

• 时间步长δt控制在1/500至1/1000时定价误差较小，过小时误差反而增加。

障碍期权定价方法及实证效果对比 [page::13][page::14][page::16][page::18][page::19]

• 解析解可用于特定障碍期权作为基准，障碍价需根据观察频率调整（向下敲出看跌期权障碍价下调）。

- 普通蒙特卡洛模拟估值误差大且收敛速度慢，条件蒙特卡洛和重要性采样显著提升定价稳定性与精度。

• 重要性采样通过调整漂移项bp提升突破障碍价路径比例，参数bp取30时误差最低，定价误差由0.38%降至0.02%。

- 有限差分法误差最小（0.09%），对参数价格步长敏感，控制在0.5以内误差较小，收敛效率最高。
| 定价方法 | 平均定价误差绝对值 |
|--------|------------------|
| 普通 MC | 1.40% |
| 条件 MC | 0.17% |
| 重要性采样 | 0.15% |
| 有限差分法 | 0.09% |

亚式期权定价中的蒙特卡洛模拟改进技术 [page::19][page::20][page::21][page::22]

• 普通MC收敛缓慢，需约20万路径；通过控制变量法，利用价格总和Y作为控制变量，收敛速度显著提升，路径数减半，区间宽度减半。

- 低差异序列（Halton序列）生成的随机数更均匀，增强模型稳定性，收敛速度最快，约需5万路径完成收敛。

• 长期期权价格对Halton序列准确度有影响，适合短期期权定价。

结论总结 [page::23][page::24]

• 树模型适合美式期权，有限差分法在计算效率及准确度上均优于二叉树，适合无解析解期权排布求解。

- 蒙特卡洛模拟适用范围广，能支持复杂条款期权定价，关键在于采样技术改进以提升收敛效率和稳定性。

• 有限差分法定价更快且更准确，适合边界条件明确、结构较简单的期权。

- 三种蒙特卡洛改进方案（控制变量、重要性采样、低差异序列）均显著提升模拟效率，是复杂期权定价的推荐路径。

场外期权定价模型初探——深度分析报告

---

1. 元数据与概览

报告标题：场外期权定价模型初探
分析师：邢维洁
发布机构：湘财证券研究所
发布日期：未明确具体日期
主题：期权定价模型及其在场外期权（美式、障碍、亚式）定价中的应用分析
联系方式：021 50295374；邮箱：xwj06627@xcsc.com

核心论点与主要内容：

本报告旨在系统介绍和分析几种常见场外期权定价模型的理论基础及实证应用效果，主要涵盖树模型（主要是二叉树）、蒙特卡洛模拟及有限差分法三大类方法。通过深入剖析这三种模型的数学背景、算法实现、计算效率和定价准确性，结合美式期权、障碍期权以及亚式期权三种重要场外衍生品，研究不同模型的适用性与优劣。

报告结构清晰，包含定价模型概述、具体产品定价应用及风险提示。结论指出，有限差分法在满足特定条件下提供定价准确且高效的方案，蒙特卡洛模拟因灵活性强适应结构复杂的期权，但原始MC收敛慢，改进技术（控制变量、低差异序列、重要性采样）显著优化定价性能。

风险提示强调模拟定价结果基于模型设定与仿真，不构成具体投资建议。[page::0,1]

---

2. 逐节深度解读

2.1 期权定价模型概述

• 资产价格模型：报告从资产价格的涨跌建模入手，基于标的价格离散时间分段构建$S{t+1} = ut St$乘数形式价格模型。随机变量$ut$对数服从正态分布，从而$St$服从对数正态分布，符合经典的几何布朗运动框架。
• 维纳过程：引入维纳过程作为连续时间下资产价格随机驱动部分的数学描述，强调其独立增量和正态分布特性，是随机微分方程（SDE）中噪声项的基础。
• 伊藤引理：作为理解资产价格过程和期权定价偏微分方程的核心，报告详细推导伊藤引理的过程，说明如何从单变量随机过程推导函数的微分形式，保持随机微分项的展开，体现随机分析数学基础。
• Black-Scholes方程推导：基于无套利构造对冲组合推导期权价格任选价格$S$和时间$t$的偏微分方程。方程为：

$$
\frac{\partial f}{\partial t} + r S \frac{\partial f}{\partial S} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 f}{\partial S^2} - r f = 0
$$

该方程是欧式期权定价的数学基石，许多数值解法基于此构建。[page::2,3,4,5]

2.2 定价模型介绍

• 树模型：以二叉树模型为代表，模型对资产价格的涨跌设定对应参数$u, d$及风险中性概率$p$，可通过后向递推计算期权价格，适合美式期权因考虑提前行权。多步长二叉树通过构建价格节点构成树形结构预测标的价格路径。
• 蒙特卡洛模拟：通过生成大量资产价格路径（基于几何布朗运动），计算各个路径的期权收益，并对收益进行折现和均值统计，得到期权价格估计。报告指出模拟路径数量对定价结果的收敛性和精度影响显著。
• 有限差分法：将BS偏微分方程离散化成差分方程，通过显式差分、隐式差分和Crank-Nicolson方法进行数值求解。其中Crank-Nicolson方法结合显式与隐式方法优点，提高计算稳定性与效率，由六个邻近网格点估计偏导数以迭代求解价格。

图示（图1~3）清晰展现了单步和多步二叉树模型结构，及三种有限差分方案的网格点计算方式，帮助理解模型的区别与适用场景。[page::6,7,8,9,10,11]

---

2.3 场外期权实证应用分析

2.3.1 美式期权定价

• 模型对比：二叉树模型与有限差分法都可有效定价美式期权。二叉树优势在于精确嵌入提前行权逻辑，有限差分法则依赖迭代技术解决无明确边界条件（提前行权导致期权价值必须大于内在价值），实现计算时通过松弛因子$\omega$控制收敛速度。
• 参数优化：

- 松弛因子$\omega$在(0,2)范围试验，$\omega >1$时与二叉树模型价格误差最小（图4）。
- 时间步长$\delta t$的选择对误差影响不容忽视，步长过小（小于约1/1200）误差反而增大（图5）。

• 效率比较：有限差分法计算时间约0.0076秒，显著优于0.2013秒的二叉树算法，且两者精度基本一致。总体看，有限差分法在美式期权定价上具有更优的计算效率和灵活性。

2.3.2 障碍期权定价

• 产品特点：敲出／敲入期权依赖标的价格是否触及某一障碍价$Sb$，实际观测多为离散间隔，使敲入/敲出概率偏离连续观察假设。
• 解析解：向下敲出看跌期权具有Closed-form解析解，式中涉及多项累计正态分布函数（$N(di)$），参数表达式复杂但详尽（如$a$, $b$, $d1$\textasciitilde $d8$），用于标杆定价。
• 障碍价调整：为应对离散观察导致障碍价检查概率低，采用Riemann-Zeta调整方法，障碍价按

$$
Sb \to Sb e^{\pm 0.5826 \sigma \sqrt{\delta t}}
$$

进行适当修正，确保定价更接近市场观测。

• 蒙特卡洛改进策略：

- 普通MC对模拟路径数敏感，误差波动大，收敛慢，且多为零突破路径（图6）。
- 条件MC利用敲入和欧式期权价格折现形式，路径依赖降噪，误差显著缩小，100000路径时误差较小（图7）。
- 重要性采样通过调节漂移项参数$bp$提升突破概率，收敛更稳定，突破率由0.11%提升到约0.8%，定价误差由0.38%降至0.02%（图8、图9）。

• 有限差分法：设定障碍价上下界限，将$Sb$视作边界，边界条件$f(S{max}, t)=f(Sb,t)=0$，利用Crank-Nicolson方法求解偏微分方程，价格对价格步长敏感（控制在0.5以内误差低），时间步长影响甚微（图11）。
• 定价误差对比（表1）：

| 定价方法 | 平均定价误差绝对值 |
|------------|----------------|
| 普通MC | 1.40% |
| 条件MC | 0.17% |
| 重要性采样 | 0.15% |
| 有限差分法 | 0.09% |

有限差分法误差最低且计算效率最高。MC方法灵活但原始误差大，改进后显著提高效果。[page::12-19]

2.3.3 亚式期权定价

• 产品特征：标的均价决定最终兑现，表现较强路径依赖，传统解析解不完全适用。
• 蒙特卡洛模拟：

- 普通MC：模拟结果随路径数增加逐渐收敛，但收敛速度缓慢，200000路径后价格及区间宽度趋稳（图12）。
- 控制变量法：
- 选取标的价格总和$Y=\sumi S(ti)$作为控制变量，通过计算$E[Y]$和相关系数调整期权价格，有效减小方差。
- 收敛速度提高，所需路径数约减半，区间宽度缩小一半（图13）。
- 低差异序列法：
- 运用Halton序列替代传统伪随机数，生成分布更均匀的随机点，避免抽样偏斜（图14）。
- 模拟结果更平稳，收敛速度明显提升，约50000路径即可达到控制变量法100000及普通MC 200000路径的收敛水平（图15）。

• 局限性：

- Halton序列随着维度（即期限长度）增加，生成随机数精度下降，应更适合短期限期权定价。

总体而言，针对亚式期权，蒙特卡洛模拟是主要策略，通过引入控制变量和低差异序列等技术，实现较好的计算效率和准确度。[page::19-23]

---

3. 图表深度解读

图1 & 图2（单步长和多步长二叉树模型）：清晰展示标的价格的离散涨跌路径，节点数随步数线性增加，理论上提供美式期权适用框架，易加入提前行权判断。[page::6]

图3（三种有限差分法示意）：突出差分法的网格点依赖关系及向前、向后、中央差分的实现差异，明确Crank-Nicolson结合两时间层优点，提高解的稳定性。[page::9]

图4 & 图5（美式期权有限差分参数优化）：

• 图4显示$\omega$松弛因子调整对误差显著影响，$\omega >1$时误差最低，定价结果接近二叉树。

- 图5表明时间步长过小时，误差反而上升，步长选取需平衡稳定性与精度。[page::12]

图6—10（障碍期权MC模型参数优化）：

• 图6展示普通MC的价格与误差随路径数波动大，区间宽度宽。

- 图7（条件MC）误差波动较小，路径数10万以上误差可控。

• 图8（重要性采样）显示漂移参数$bp$调整突破次数与定价误差的关系，存在最优区间。

- 图9表明路径数20万以上，重要性采样误差稳定且收敛更快。

• 图10总结三种MC方法在误差及区间宽度上的对比，重要性采样显著优于其它两种。[page::14-17]

图11（有限差分价格步长敏感度）：价格步长小于0.5时定价误差较低且稳定，价格步长逐步增大误差扩大，反映空间网格刻度选择重要性。[page::18]

表1（障碍期权定价误差对比）：结构清晰展示各方法优劣，有限差分误差最低，普通MC最高。[page::19]

图12—13（亚式期权MC方法收敛效果）：

• 图12显示普通MC收敛慢，区间宽度大。

- 图13控制变量法显著缩减收敛路径数与区间宽度，提高计算稳定性。[page::20-21]

图14（随机数分布对比）：

• 普通MC随机散点不均匀，可能遗漏部分样本空间。

- Halton序列分布均匀，有利于减小方差，提高模拟效率。[page::22]

图15（亚式期权三种MC收敛对比）：

• Halton序列收敛速度最快，价格波动最小。

- 控制变量次之，普通MC收敛缓慢且价格震荡大。从路径数对比看效率提升明显。[page::22]

---

4. 估值分析

本报告未涉及具体公司或市场环境估值目标价的内容，属于模型理论与实证研究范畴，不涉及股票等传统估值指标。

报告中涉及的估值是纯期权定价中的理论价值计算，使用的主要是：

• 树模型估值（CRR二叉树）：基于无套利概率修正标的价格后的期权价值期望折现。
• Black-Scholes偏微分方程及有限差分法求解：利用确定性偏微分方程离散化计算期权理论价格。
• 蒙特卡洛模拟估值：通过大量随机路径模拟资产价格，计算期权期末收益的折现平均。

重要的是，报告详细探讨了蒙特卡洛法中样本路径数、方差减小技术（控制变量法、重要性采样、低差异序列）的参数优化，直接影响估值精度与计算效率。

在障碍期权重要性采样中，漂移参数$bp$的调整显著影响突破路径比例，进而影响定价误差，展示了对于关键参数的敏感性分析。

在有限差分法中，时间步长和价格步长的选择对解的稳定性和误差控制有明显影响，尤其价格步长小于0.5时误差处于最低水平。

综上，报告通过数学模型、数值方法与计算优化对期权定价估值进行了全面剖析。[page::6-22]

---

5. 风险因素评估

报告明确提出风险提示强调：

• 本报告基于模型设定的理论或模拟数据，不构成任何具体投资报价或建议。

- 定价结果为模拟数据，并非真实市场价格，应理解模型假设和现实情况的差异。

• 模型的适用性、参数选择及计算精度在一定程度上影响结果的稳健性。

- 期权价格受到市场波动、标的资产价格波动率、利率变动、观察频率等多重因素影响，模型假设与实际市场条件可能不完全吻合。

具体缓解策略体现在采用更稳定的数值方法（如Crank-Nicolson法）、方差减小技术以及参数优化，目标降低模型误差和计算时间，但仍需注意模型潜在偏差风险。

此外，障碍期权的价格观测频率不足可能产生估值低估，进行了障碍价调整以校正。

风险说明清晰，适当提醒了模型应用的局限性及风险承担责任。[page::0,25]

---

6. 批判性视角与细微差别

• 依赖模型假设：报告基于几何布朗运动假设，现实中资产价格可能存在跳跃、波动率微笑等复杂现象，模型在极端情况下误差可能增大。
• 参数敏感性：尽管部分分析表明模型对参数不敏感（如有限差分美式期权中松弛因子、时间步长），但蒙特卡洛模拟中路径数量及重要性采样参数对结果影响极大，实际应用中参数选择仍需要谨慎。
• 奇异期权与复杂条款处理：有限差分法优势明显但局限于偏微分方程具体条件，结构复杂或含多层障碍条款的期权无法直接使用，蒙特卡洛仍是不可缺替方案，但计算成本意见显著。
• Halton序列局限：报告指出低差异序列的准确率受期权期限影响，期限越长误差越大，提示在跨期较长的期权定价中可能需要改进方案。
• 数值边界条件设定：有限差分法的边界条件设定对于定价结果至关重要，尤其对于障碍期权上下边界，需要确保其合理有效，否则可能引入偏差。
• 未涉及市场流动性风险：虽然模型偏重理论定价，未讨论市场实际流动性、交易成本等影响，实务中这些因素不可忽视。

总体而言，报告内容科学严谨，具备较强的理论深度与实证支撑，但在实际应用中仍需结合市场实际动态修正与扩展模型。

---

7. 结论性综合

本报告系统介绍了期权定价领域三类主流数学模型——树模型、蒙特卡洛模拟及有限差分法的理论基础和实际应用框架，特别聚焦于美式、障碍及亚式期权等场外复杂衍生品。

核心发现包括：

• 理论基础：资产价格遵循几何布朗运动，基于维纳过程和伊藤引理推导出的BS偏微分方程构成定价基石。
• 模型特点与适用：

- 树模型（CRR二叉树）：结构清晰，适合美式期权，方便嵌入提前行权判断，但计算效率相对有限差分偏低。
- 蒙特卡洛模拟：灵活适用结构复杂的奇异期权，路径依赖期权首选，但收敛慢、误差大，需要借助控制变量法、重要性采样和低差异序列提升效率与精度。
- 有限差分法：精度高、计算效率优于树模型和普通蒙特卡洛，尤其对欧式及部分障碍期权模型精确度优异，但对期权结构有特定限定。

• 实证对比：

- 美式期权定价中，有限差分法较二叉树计算快20倍左右，参数优化使结果接近。
- 障碍期权有限差分法误差最低（0.09%），重要性采样次之，普通MC误差最大（1.40%）。
- 亚式期权蒙特卡洛模拟中，控制变量法、Halton序列方法的收敛速度分别约为普通MC的2倍和4倍。

• 图表揭示：

- 价格路径模型（图1，2）与差分法结构（图3）为原理基础。
- 参数敏感度图（图4~5，8~9，11~13），直观体现调整关键参数对结果收敛和准确度的影响。
- 各MC模拟方法收敛比较（图6~10，12~15），有力印证先进MC方法提升定价效率和稳定性。

• 风险提示明晰强调价格为模型输出模拟结果非实盘价，模型设定及参数变化可能引发偏差，投资需谨慎。

总之，本报告为理解和应用场外期权定价提供了扎实理论基础与丰富实证数据支持。针对不同期权产品的特性，合理选择定价模型和相关数值方法，结合参数优化和方差减小技术，是实现精准高效期权估值的关键。未来针对路径依赖及复杂条款的期权，需要进一步集成多模型优势及加强对参数动态调整的研究，以贴近市场实际定价需求。[page::0-25]

---

参考图片示例

图1：单步长二叉树模型


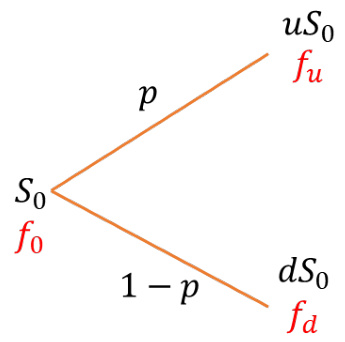
图4：有限差分法定价美式期权的参数优化（松弛因子𝜔）


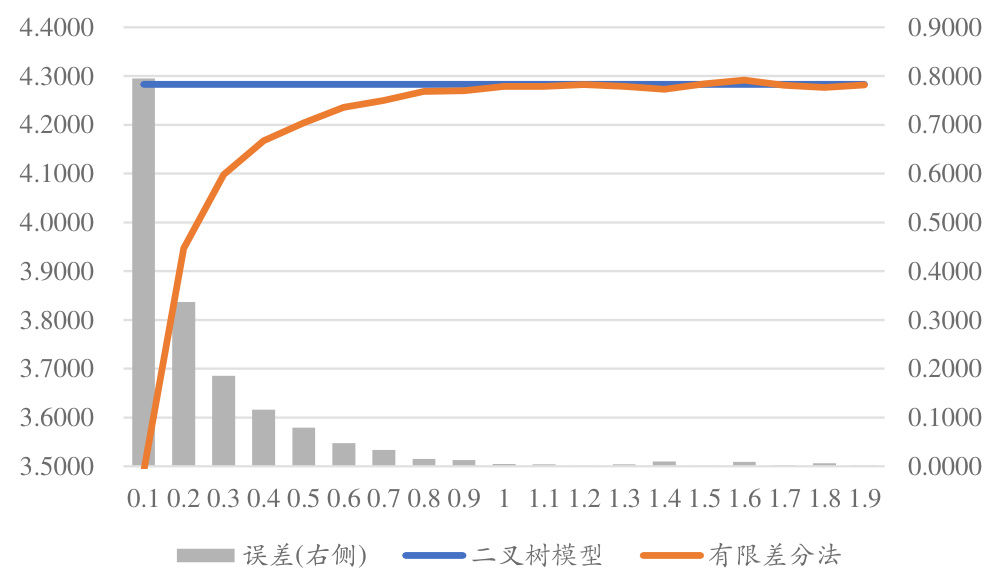
图8：重要性采样蒙特卡洛模拟参数优化结果（漂移项调整参数$bp$）


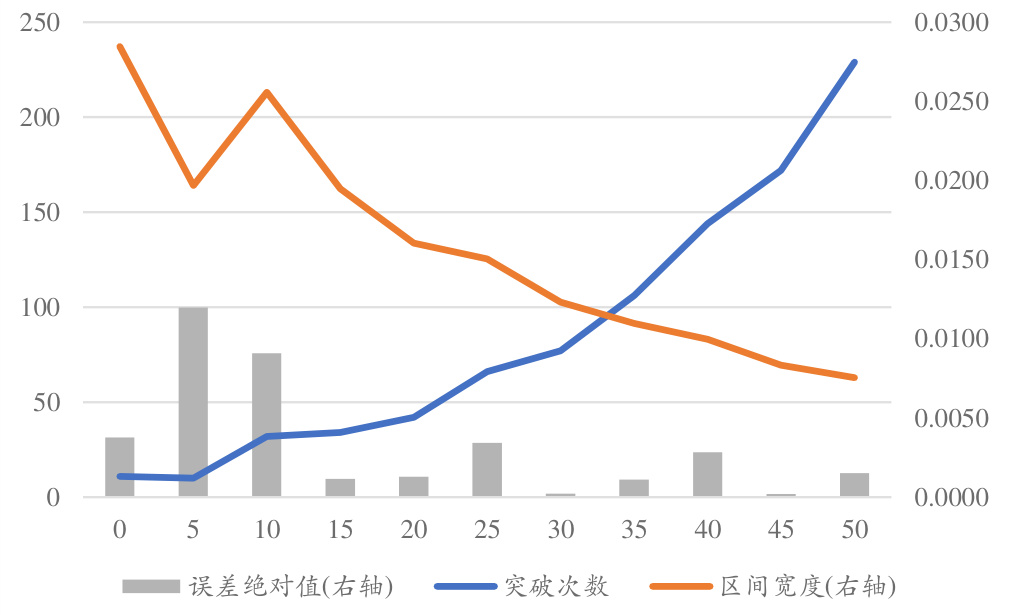
图15：三种蒙特卡洛模拟的定价结果对比（模拟路径数量）


---

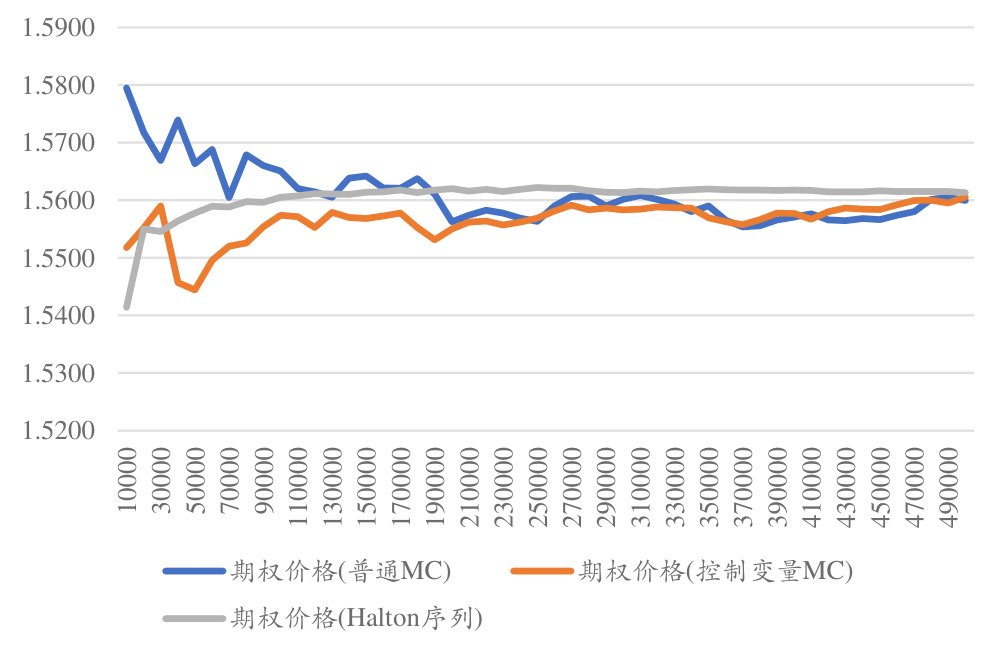
综上所述，本报告提供了细致、权威且系统的期权定价模型分析，适合从业者理解常用期权模型及其优化技术在实际场外产品中应用的效能和风险，具备良好的理论和实务结合指导意义。

报告