• 研究背景与模型设定 [page::1][page::2]:

- 市场主体包括一个离散时间点交易的大交易员(LT)和一大群连续交易的高频交易员(HFTs)。
- HFTs具备对LT未来订单进行预测能力，并拥有不同且动态变化的库存厌恶水平。
- LT追求收益最大化，HFTs兼顾收益和库存风险控制。

• 价格影响与交易成本模型 [page::3][page::4]:

- 价格包含永久性和暂时性价格冲击，其中HFT和LT分别对价格产生影响，且存在交易费用。
- LT实际成交价格包含自身交易量相关暂时性冲击和HFT整体交易行为的影响。

• 均场博弈解法与均衡定义 [page::4][page::5]:

- 采用均场博弈方法解决大量HFTs导致的维度灾难问题。
- 定义部分纳什均衡（LT策略固定时HFT均衡）和整体纳什均衡（LT和HFT策略联立均衡）。
- 均衡策略为马尔可夫反馈型，涵盖HJB偏微分方程及Kolmogorov前向方程的耦合系统。

• HFT最优交易策略与演化方程 [page::6][page::7][page::8]:

- HFT最优控制变量为交易速度，策略解由对应的HJB方程和Riccati方程组确定。
- 库存与交易速度的均值演化满足耦合微分方程，考虑HFT的库存态和跳跃风险厌恶转移。
- 在每个LT交易时间点，HFT交易速度出现跳跃体现预期LT交易影响。

• 特殊与一般情况数值解法 [page::9][page::10]:

- 单一库存厌恶水平情况下的系统可解析求解。
- 多级库存厌恶情况采用数值解耦合微分方程组及线性代数方法进行求解。
- 证明了当HFT数目足够大时，均场解逼近有限HFT的ε-纳什均衡。

• LT与HFT的整体均衡策略 [page::11]:

- LT在考虑HFT平均交易行为影响下求解最优交易策略，形成线性方程组求解。
- 证明当HFT数量增加时，整体均衡解为有限参与者博弈的良好近似。

• 数值实验分析主要发现 [page::12][page::13][page::14][page::15][page::16]:

- HFT库存厌恶度增加使其表现为Round-Tripper角色，先同向交易再反向补偿，验证外部文献经验结果。
- HFT的暂时性价格冲击越大，LT从中受益越明显。
- 跳跃转移率改变HFT厌恶态分布，影响其交易行为模式及LT利润。
- 在整体均衡中，增加HFT对运行库存的厌恶使LT策略更接近均匀交易，体现出HFT平抑市场的效应。

• 量化因子与策略亮点：

- 本文理论构建了HFT库存风险厌恶多状态跳跃转移模型，并通过均场博弈耦合方程精确描述其策略动态。
- 翻译出HFT平均库存与交易速度的动态演化微分方程组，结合跳跃过程，体现策略的自适应调整。
- 定义并证明部分及整体均衡的ε-纳什性质，保障算法数值解的可靠性。
- 数值回测验证了预期交易行为在市场冲击及库存惩罚不同设定下的表现差异，且反映出HFT预期交易策略对LT执行路径的调节作用。

金融研究报告深度解析报告

---

一、元数据与概览

• 报告标题： Mean Field Game of High-Frequency Anticipatory Trading

- 作者： Xue Cheng、Meng Wang、Ziyi Xu

• 发布机构： 北京大学数学科学学院金融数学系 LMEQF

- 发布日期： 报告未明确具体发表日期，但引用文章多为2023年前期，推测为2023年或之后。

• 主题领域： 以高频交易者（HFT）与大宗交易者（大交易者，LT）在市场中的动态交互为核心，使用均场博弈（Mean Field Game）理论对其策略及市场影响进行建模与分析。属于金融数学及市场微观结构分析范畴。
• 核心论点与主要信息：

- 本文建立了一个模型研究大量高频交易者（HFT）与一个大交易者（LT）之间的交互，尤其关注HFT的提前预测（anticipatory）交易行为对LT执行策略和市场成本的影响。
- HFT交易速度连续且高于LT，LT仅在离散时间点进行交易。
- HFT们的库存规避行为（对持仓的厌恶）被建模为随时间变化的跳跃过程。
- 通过均场博弈框架，解决了众多HFT交互所导致的维度灾难问题，得出了部分以及整体纳什均衡解。
- 发现当HFT群体对持续持仓（running inventory）较为厌恶时，呈现“Round-Tripper”行为，即交易行为在大宗交易前后分别先买后卖或先卖后买，进而对LT成本有降低作用，尤其是当市场临时价格冲击较永久冲击大时。
- HFT的流动性供给-消耗行为使得LT的最优执行策略趋近均匀交易。
- 报告明确给出了均场博弈中部分和整体均衡的定义，并证明了作为有限HFT数量博弈的近似均衡性质。

---

二、逐节深度解读

1. 引言与背景（章节1）

• 关键论点：

- 阐释了高频交易者与大交易者的市场角色和互动机制，特别是HFT通过提前预测大交易者的交易行为进行的预测性交易。
- 引用实证研究（如 Sağlam 2020, Hirschey 2021）强调这一交互的实际存在和重要性。
- 建立了本研究框架：大交易者在离散时点交易，HFT持续交易且能提前预测大交易者动作。HFT库存厌恶度存在异质性且随时间跳变。
- 引入两种纳什均衡定义：部分纳什均衡（固定LT策略，求HFT均衡）和整体纳什均衡（LT与HFT同步求均衡），强调LT策略受HFT行为反馈影响。
- 深入描述了Round-Tripper策略及其经济含义，即HFT先买入预期大买单，再卖出回血流动性的行为。
- 发现的现象与实证文献吻合（van Kervel & Menkveld 2019），增强了模型的现实解释力。
- 提出当市场临时价格冲击较大时，HFT的库存规避行为降低了LT的执行成本。
- LT的最优策略受HFT流动性行为影响，可能接近无HFT情况下的均匀交易。
- 采用均场博弈方法太解决高维问题，并论证此方法对于有限大群体的博弈有良好近似效果。

• 推理和假设基础：

- 市场价格受交易者的永久与临时冲击影响。
- HFT在速度和信息处理上远优于大交易者。
- 库存厌恶有终端和持续两种形式，且可跳变动态。
- LT策略相较固定，被假设为确定性，交易节奏慢。
- 均场博弈适合描述大规模异质主体互动，避免了多主体维度问题。

---

2. 文献综述（章节2）

• 概述：

- 介绍均场博弈理论的起源、数学工具及其经典解析路径（HJB与KFP偏微分方程），并提及后来概率学方法（FBSDE）的引入。
- 讨论了扩展均场博弈（考虑主要与次要代理人）问题，明确本模型中LT是主要玩家，HFT是次要代理人。
- 指出本论文首次结合了连续时间与离散时间混合策略的均场模型，且涵盖跳跃库存规避的异质HFT。
- 并且与已有涉及HFT和大交易者互动的文献相比，有不同维度（如交易频率、速度差异、交易离散性等）创新点。

• 文献对比与创新点：

- Cardaliaguet & Lehalle (2018) 与 Jaimungal & Nourian (2019) 类似研究，但前者HFT库存规避静态，后者交易均为连续，本报告模型创新包括异质且跳变的HFT库存厌恶、交易混合离散连续时间。
- Cont et al. (2023) 研究了类似慢速机构投资者与HFT的Stackleberg博弈，但交易速度一致，缺少均场大群体分析。
- 实证支持包括 van Kervel & Menkveld (2019)、Sağlam (2020) 等。

---

3. 模型设定（章节3）

• 总体设定：

- 交易时段$[0,T]$，LT于离散时间点$\{tk\}$执行累计清仓任务，交易额为$\{\xik\}$。
- HFT以连续时间进行交易，个体持仓和交易速度分别为$Xj(t),vj(t)$，满足动力学$dXj(t)=vj(t)dt$。
- HFT的库存厌恶度取值于有限集合$\mathbb{S}$，含终端库存厌恶$\Gamma(i)$和持续库存厌恶$\phi(i)$，并以跳跃马尔可夫过程模型（转换矩阵$Q$）动态变化。
- 价格动态包括基础布朗运动波动、LT和HFT的永久价格冲击，交易费和临时价格冲击组成实际成交价。HFT群体影响价格永久冲击为$\gamma^H/M$，确保随规模变大影响不爆炸。

• LT目标函数：

- 最大化预期成交收益，考虑价格冲击和交易成本，控制策略为确定性且清仓约束严格。

• HFT目标函数与约束：

- 最大化最终财富（含标记市值及交易利润），并惩罚持有仓位风险（终端及途中惩罚）和交易手续费。
- 行为策略为适应市场信息的平方可积可右连续控制过程。

• 均场博弈定义（3.2节）：

- 随$M\to \infty$，HFT群体影响通过其加权平均交易速度体现，单个HFT影响只在交易成本费用体现。
- 定义了部分纳什均衡（给定LT策略，求HFT均衡解）与整体纳什均衡（LT和HFT均在博弈中选择策略）。
- 命题说明均衡解可用确定性函数表达（马尔可夫反馈形式），并给出均衡的固定点条件。
- 还引入有限M数量HFT下的$\varepsilon$-Nash均衡概念，论证均场解为良好的有限玩家近似。

---

4. 纳什均衡的求解（章节4）

• HJB方程与跨间断性处理（4.1节）

- 针对HFT的价值函数$H$和其偏微分方程，细分区间为LT交易时点分割的连续段，分段求解HJB方程。
- 处理$h_i(t,x)$状态函数二次形式猜想，转化为矩阵Ricatti方程组。
- 优化交易速度求解得反馈形式控制策略。
- 证明该优化满足验证定理（Thm. 1），$H$为最优值函数。
- 引入Kolmogorov前向方程，描述库存状态概率密度演化（Lemma 1, 2），建立平均库存与交易速度的动态方程。其中特别考察由于跳转库存厌恶导致的平均状态变化。
- 解得平均库存演化系统为带跳跃和不连续调整的广义矩阵微分方程，边界条件由LT交易冲击决定。
- 特别情形：单库存厌恶水平可显式求解，给出特征根及解析解结构。
- 通用N水平数值解法：先解跳转矩阵对应的概率演化$p(t)$，再求解关联微分方程组，最后利用初始和边界条件线性求解系数。

• 均衡性质保证（4.1.3节）

- 证明当HFT数量足够大时，均场解提供有效的$\varepsilon$-Nash均衡（Thm.3），保证均场方法的实际适用性。

• 整体纳什均衡（4.2节）

- LT最佳策略闭式给出，依赖HFT均衡平均库存和交易速度。
- LT策略和HFT响应构成联合线性方程组，分步骤求解。
- 同时证明有限HFT下的整体均衡近似均场整体均衡（Thm.4）。

---

5. 数值分析（章节5）

• 部分纳什均衡影响（5.1节）

- 对LT策略固定，观察HFT不同库存规避水平（$\Gamma,\phi$）时的行为。
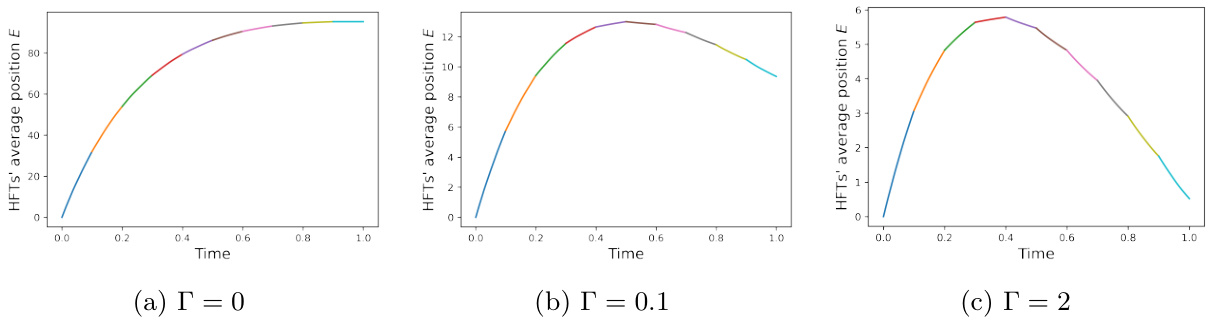
- 图1显示：当持续库存厌恶$\phi=0$且终端厌恶$\Gamma$增加，HFT表现为跨期“Round-Tripper”，持仓先增后减。
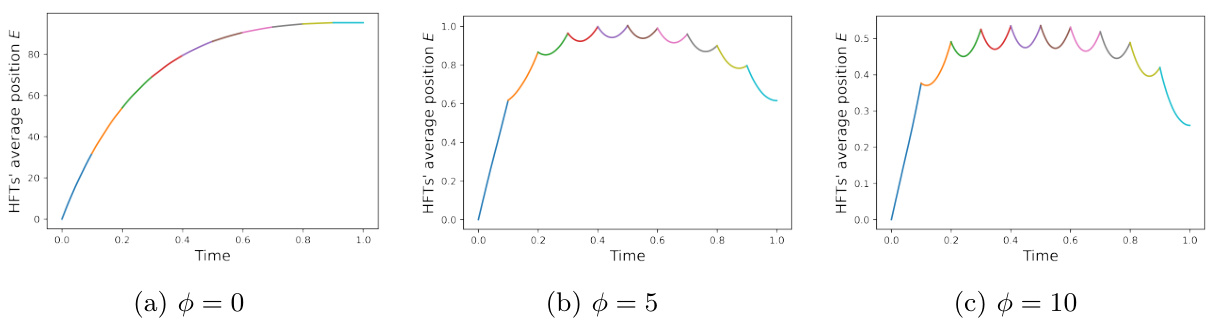
- 图2显示：当终端厌恶$\Gamma=0$且持续厌恶$\phi$增大时，HFT在LT交易多个时点内重复“Round-Tripper”行为—短周期内先做反向交易后顺向补仓。中间分析验证了现实发现：HFT先逆向交易后跟随大单方向交易（van Kervel & Menkveld 2019）。
- LT利润分析： 没有HFT时为基线利润，HFT存在时利润额外由其累计对价格的影响调整。
- 图3展示临时冲击系数提升使LT利润增加，说明临时价冲击大能降低HFT提前交易的负面效应。
- 进一步分析跳跃状态的混合库存厌恶（$Q$矩阵非零情况）对HFT行为影响显示，跳转机制增强了HFT的库存控制意识，使其行为更趋向Round-Tripper，继续提升LT利润。
- 图4和5分别展示不同参数组合（终端/持续库存惩罚不同）的库存路径行为，反映了跳跃参数$Q$对HFT策略微妙调节。

• 整体纳什均衡影响（5.2节）

- LT策略明显受HFT库存厌恶影响。无HFT时LT均匀分配交易量（基线策略）。
- 图6-8表明：
- 终端库存厌恶低时，LT策略偏向前期成交，HFT同向交易抬升交易成本；
- 终端厌恶高，HFT表现Round-Tripper，LT倾向延后交易时间，尤其后半段加大交易量；
- 持续库存厌恶高时，LT策略趋于均匀成交，因为频繁的HFT对冲行为稳定市场价格，有利LT平滑执行。
- 图9-10对比部分和整体均衡中HFT持仓和LT利润，确认上述影响结论。
- 混合跳跃库存厌恶情形下，LT策略和HFT持仓也对应调整，HFT对市场影响逐步在整体均衡中反馈至LT最优执行。

---

6. 结论（章节6）

• 本文提出一个新颖的均场博弈模型，模拟大量异质高频交易者对大交易者离散执行的预测交易及其市场反馈。

- HFT异质的库存规避机制通过跳跃马尔可夫过程建模，模拟其交易行为动态演变。

• 两种纳什均衡形式定义及相应的数值解法与理论验证，保证均场解的适用性和近似准确率。

- 发现库存厌恶不同的HFT产生差异化的Round-Tripper行为影响市场流动性，显著调节LT的交易策略和成本。

• 当临时冲击大，HFT提供的流动性更有效，LT利润提升，且LT策略趋于均匀化。

- 文章指出未来研究方向包括引入执行风险和研究HFT学习及预测LT行为等。

---

三、图表深度解读

图1~图2：HFT平均持仓路径随库存厌恶变化

• 描述： 图1固定持续厌恶$\phi=0$，观察终端厌恶$\Gamma$的影响。图2相反，固定$\Gamma=0$，观察持续厌恶$\phi$的影响。

- 数据与趋势解读：
- 图1(a)-(c)显示，$\Gamma=0$时，持仓单调上升，说明HFT沿大单方向交易且未及时平仓；$\Gamma$增大，持仓先升后降，典型Round-Tripper特征。
- 图2(b)-(c)展示持续厌恶增加引起交易持仓多次波动，代表每次LT交易时段内的快速建仓和平仓（典型短周期Round-Tripper行为）。

• 文本联系： 验证了文中关于库存厌恶影响下HFT交易策略的理论推断，也吻合文献实证（van Kervel & Menkveld 2019）。

- 局限性分析： 无明显局限，但参数设置固定，实际市场异质性更复杂。




---

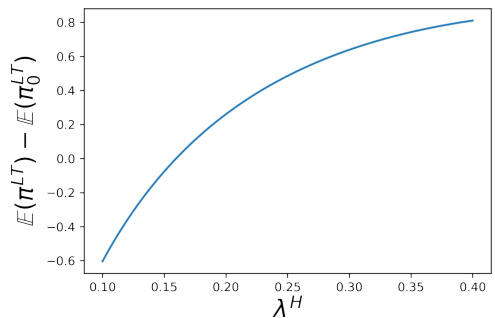
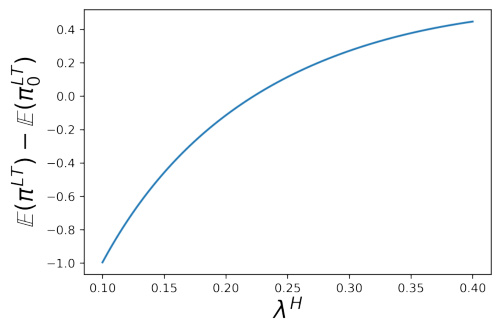
图3：LT利润差异随临时冲击系数变化

• 描述： LT由于HFT出现Round-Tripper行为时利润相较无HFT时的增量，随着临时冲击$\lambda^H$变化曲线。

- 趋势解读： LT利润随着临时冲击增强单调增加，从负收益快速转为正收益，说明临时冲击大使HFT的先同向后逆向交易更有利于LT。

• 逻辑对应： 临时价冲击大的市场更具弹性，HFT卖盘回补流动性快，减少不利价冲击。

- 潜在局限： 未显示永久冲击参数变化影响，仅单因素分析。



---

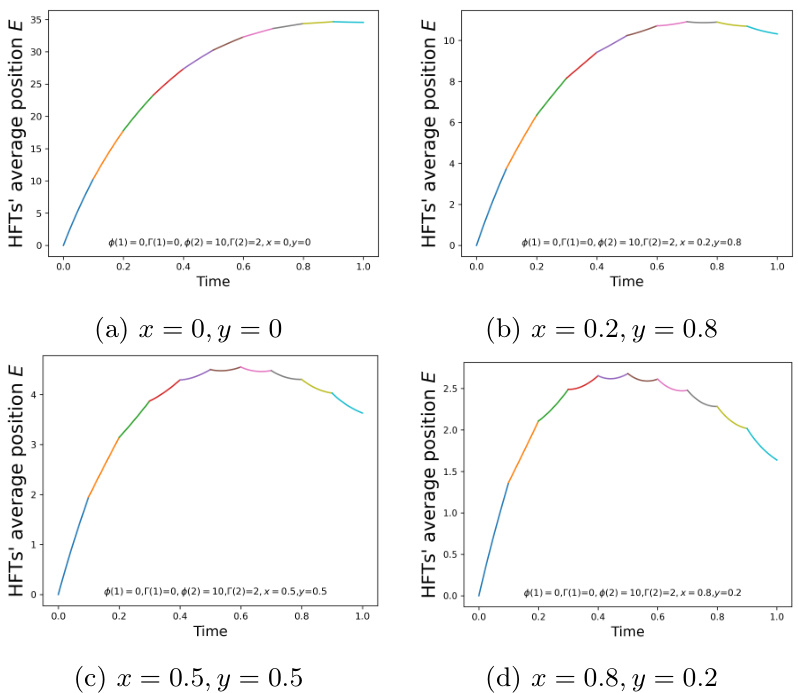
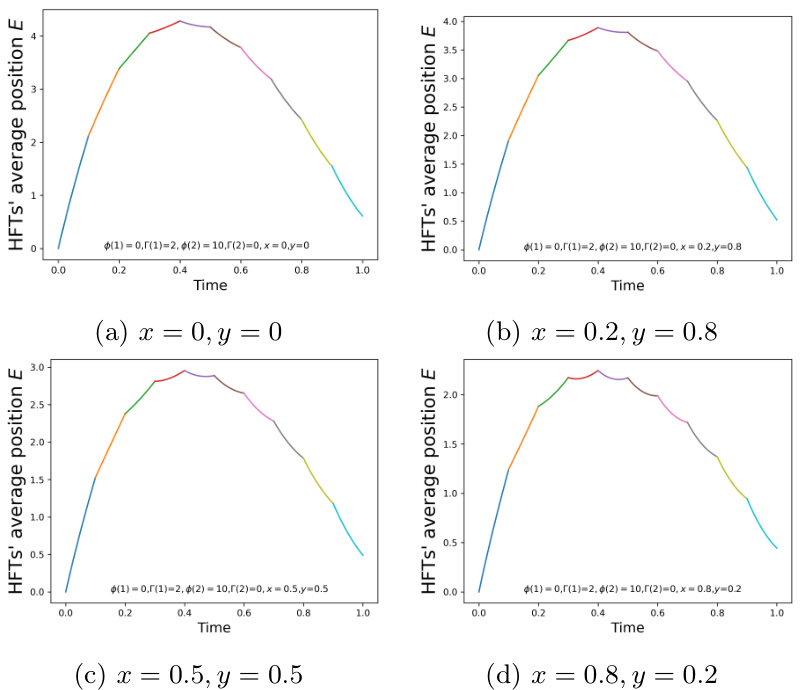
图4~图5：跳跃库存厌恶参数变化对HFT持仓的影响

• 描述： 二状态跳跃库存厌恶模型，其中部分HFT库存厌恶为零，部分较高，$Q$矩阵参数$(x,y)$控制跳跃概率分布；图4状态一套参数，图5另一套。

- 趋势解读：
- 没有跳跃（$x=y=0$），部分HFT累积仓位显著；跳跃存在后，HFT整体持仓更趋Round-Tripper特征；不同跳转权重引导HFT对terminal或running inventory更厌恶，进而细微调整其交易策略。

• 文本支持： 进一步验证库存厌恶跳转机制使HFT更合理控制仓位，提高模型现实相关性。

- 图文联系： 支持作者对异质HFT行为动态的设计及经济诠释。




---

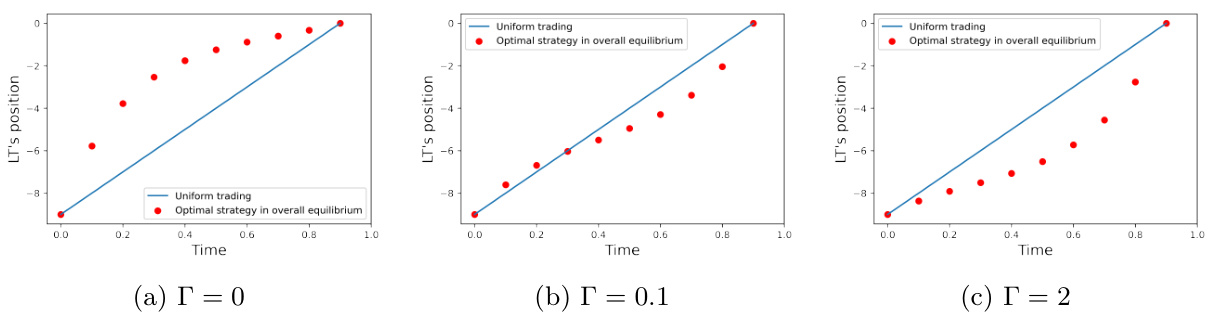
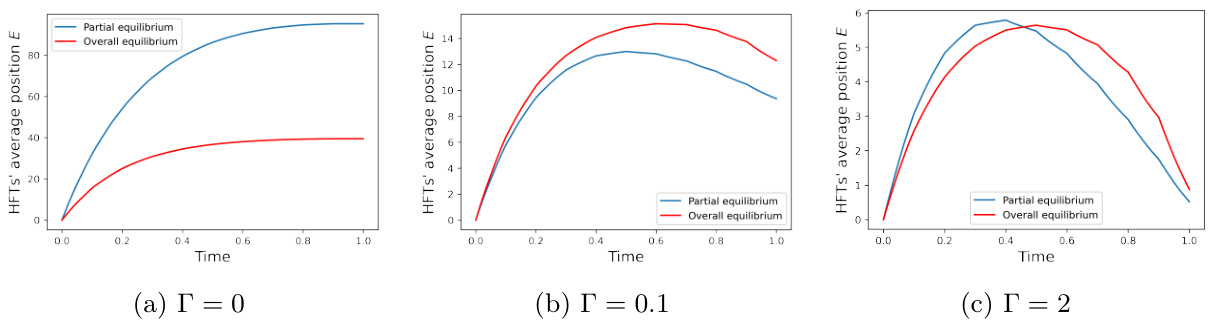
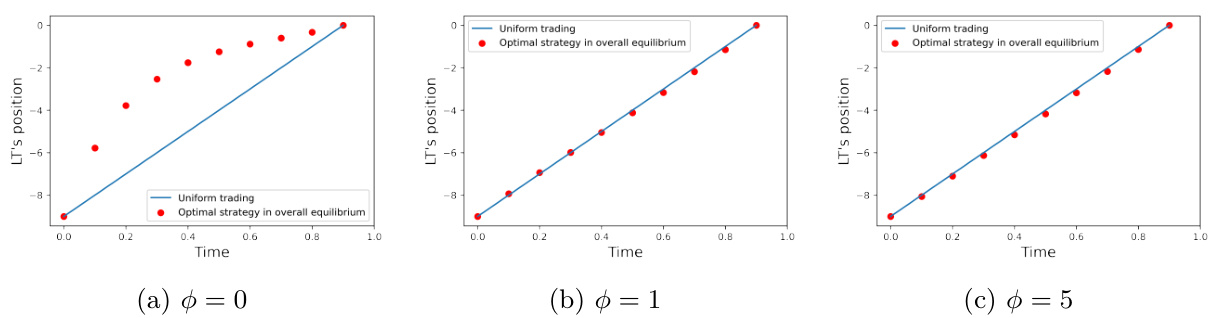
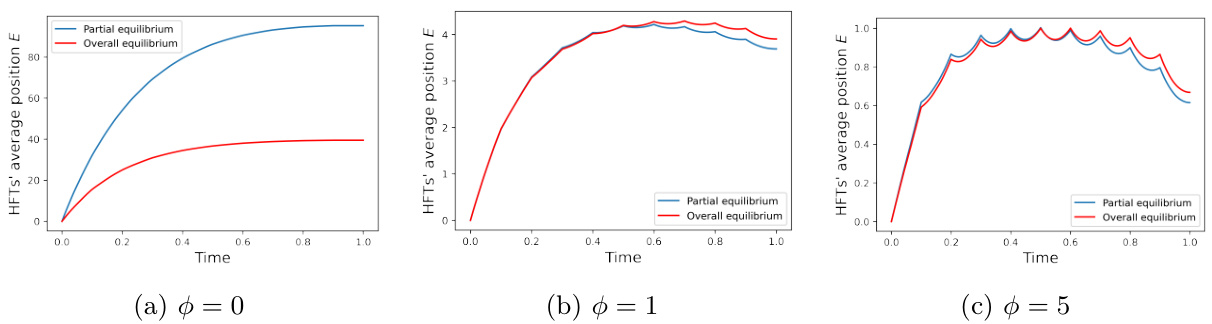
图6~图10：整体均衡中LT及HFT策略与利润表现

• 描述与趋势：

- 图6显示无HFT时LT采取均匀策略，HFT存在时，LT策略根据HFT库存厌恶调整，非零$\Gamma$促使LT延迟交易。
- 图7~9对比部分/整体均衡中HFT持仓和LT策略，整体均衡更平滑。
- 图10针对利润变化随临时冲击比较，确认整体均衡中LT经济效应提升。

• 关键推断：

- HFT持续库存厌恶使LT交易更均匀，降低价格波动性，有利交易执行。
- 交易策略调整体现了HFT流动性模拟对交易环境的实际优化。

• 局限性：

- 模拟参数固定，实际市场异质复杂，风险因素等未完全纳入。







---

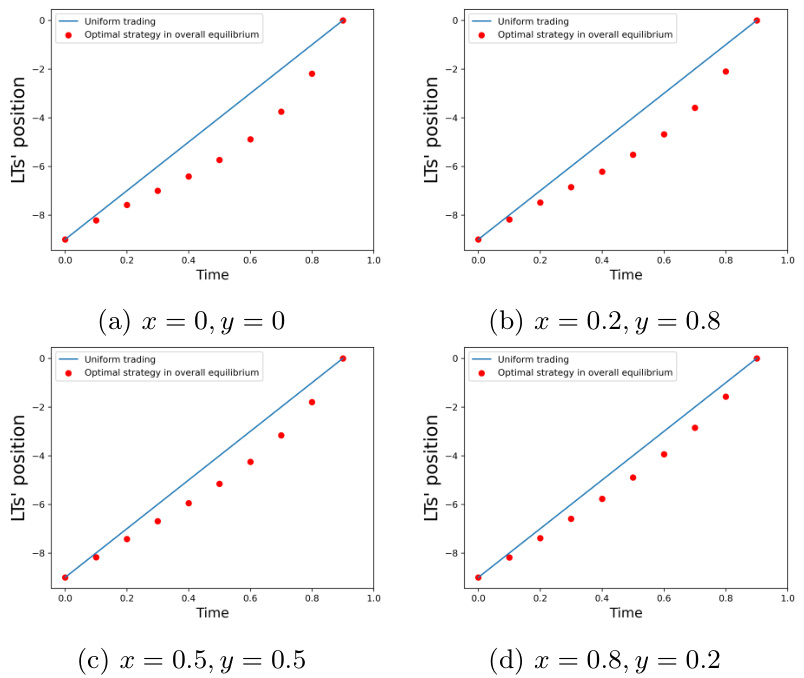
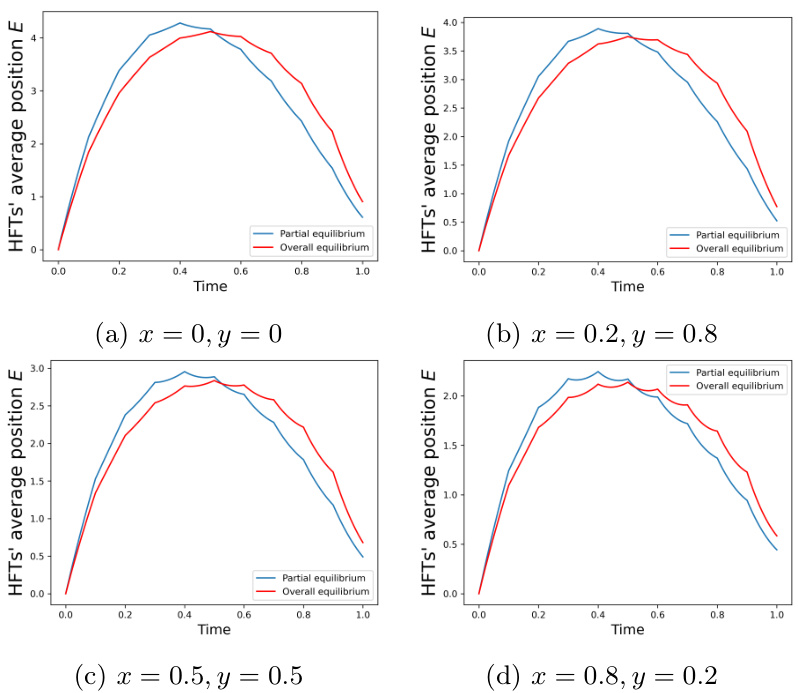
图11~图12：混合跳跃库存厌恶下LT和HFT持仓策略

• 描述： 不同跳跃参数$x,y$调整HFT的running和terminal厌恶程度，考察对应下LT策略（图11）和HFT平均持仓（图12）。

- 趋势：
- $x$大时HFT更厌恶持续库存，LT策略趋向均匀分配；$y$大时HFT更注重终端仓位控制。
- 各种跳跃权重下均衡策略均保持与理论预期一致的Round-Tripper特征。

• 对全文贡献： 验证模型处理异质性跳跃库存厌恶的能力，为实务策略提供稳健性和动态反应参考。

---

四、估值分析

• 本文并未涉及传统意义上的估值分析（如DCF、市盈率等），其核心关注为策略优化和均衡解构建。

- 主要通过求解均场博弈中的HJB方程及相关ODE系统评估执行成本、利润和控盘行为。

• 数值部分则通过参数敏感性模拟展示不同策略和市场冲击参数影响的相对经济效益。

---

五、风险因素评估

• 文章中隐含和明确关注如下风险因素：

- 价格冲击风险： 永久和临时冲击参数设定影响市场价格走势和交易成本。
- 库存风险： 持仓的终端和运行风险通过惩罚函数体现，影响HFT交易节奏。
- 交易速度和信息不对称风险： HFT和LT交易速度差异及预测能力不完全可能导致策略失效。
- 市场流动性风险： 大交易对流动性的影响及其恢复速度，关联临时冲击参数。

• 缓解策略主要在于HFT库存厌恶，激励HFT在流动性提供和资产风险之间寻找平衡。

- 报告未细化极端市场波动或异常事件的影响，留待后续研究。

---

六、批判性视角与细微差别

• 偏见或假设限制：

- 假设LT策略完全确定，忽略其对市场信息的动态反馈能力，现实中可能偏弱。
- HFT之间的独立性和同质性假设可能忽视HFT内部策略多样和协同行为。
- 跳跃矩阵$Q$的恒定性假设相对简化，没有考虑市场环境的非平稳性。
- 模型未直接纳入市场执行风险、交易延迟、清算失败等实务问题。
- 采用均场博弈解决“维度灾难”，但个体行为的极端影响和小众策略未完全捕获。

• 内部细微差异或矛盾：

- 模型强调LT受HFT行为影响趋于均匀交易，但针对高终端厌恶的规则又显示LT有延迟行为，反映策略可能依赖细节参数平衡。
- 部分数值模拟中HFT持仓波动较大，与流动性预期稳定性稍有矛盾，但可理解为跳跃过程引发短期扰动。

---

七、结论性综合

本报告构建并深入分析了一个创新的均场博弈模型，具体研究了大量高频交易者以持续交易速度预测并响应离散时间大交易者交易的动态交互机制。HFT的库存厌恶以跳跃马尔可夫过程动态建模，赋予策略时间与状态的异质性。

模型充分考虑了市场价格中的永久与临时价格冲击，通过耦合HJB方程与Kolmogorov前向方程，解决了混合离散-连续时间框架下的均衡问题，且具备有限玩家近似的$\varepsilon$-Nash性质，保证理论与实务之间的严密联系。

数值结果确认：

• 终端库存厌恶增强时，HFT采取跨期Round-Tripper策略，LT相应延迟交易以利用HFT流动性；

- 持续库存厌恶加强，HFT实行近似于每笔LT交易的Round-Tripper策略，令LT最优执行更趋均匀化，平滑交易；

• 临时价格冲击相对较大时，HFT行为降低执行成本，提升LT利润，表明市场弹性和流动性对交易策略收益影响关键；

- 跳跃库存厌恶模型揭示异质性动态调整对策略的细微且重要的调节作用。

本研究为理解和量化高频交易者与大宗交易者间的复杂互动，尤其是预测性交易及其对市场流动性和交易成本的影响，提供了坚实的数学与经济模型基础。该模型兼具理论深度与实践指导意义，适合后续纳入更多市场现实因素如执行风险和学习行为，以进一步完善金融市场微观结构的科学理解。

---

（全文引用均依据页码标识，如需精准溯源，详见文本各段末页码标注）[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]

报告