• 研究了多种一因子Cheyette模型的局部波动率函数形式，包括线性短期利率波动率（LinSRLV）、线性基准远期利率波动率（LinBRLV）、线性Cheyette因子波动率（LinXLV）及分段线性基准远期利率波动率（PwLinBRLV）[page::2]。

- 随机波动率模型主要选用无关的CIR随机方差（CIRSV）和关联的具有二次漂移的对数正态随机波动率（QDLNSV）两种，且关注它们对定价和标定的影响[page::3][page::4]。

• 采用通用脚本模拟框架（GenSimFW）支持向TensorFlow、JAX、NumPy等后端生成MC定价器，涵盖复杂模型和参数变化，实现高效蒙特卡洛模拟和定价[page::4][page::7][page::8]。

- 利用参数化微分机器学习（PDML）方法加速定价函数学习，结合模型参数和状态变量，提升标定速度与精度，支持参数敏感度计算[page::13][page::14]。

• 标定工具链支持代码生成的MC定价器及PDML训练结果，与外部全局与局部优化算法（如ICDE、SciPy优化器等）配合执行参数拟合[page::10][page::11][page::15]。

- 重点标定结果：
- 传统LinBRLV+无关CIR SV模型难以在1年期全行权价区间完美拟合Caplet笑脸，中间执行价偏差较大[page::1][page::17]




- 分段线性局部波动率PwLinBRLV + 无关CIR SV显著提升了拟合效果，价格误差均在2个MC标准误内，适合手动调整锚点执行价以细调[page::19]



- 局部波动率取线性Cheyette因子（LinXLV）及带关联QDLNSV时表现优秀，数值结果价格误差几乎在2个MC标准误内，能重现市场1年期笑脸，包括中间执行价段[page::20]



- 使用QDLNSV随机波动率时，无论基准远期利率局部波动率（LinBRLV）还是短期利率局部波动率（LinSRLV），标定效果较无关CIR SV均有明显提升[page::21][page::22]




- 多期限校准显示LinBRLV+QDLNSV模型在1年至6年期限区间内均可良好拟合市场价格，误差控制在2个MC标准误范围，具备较强稳定性和一致性[page::23][page::24]

• 结论明确指出，结合分段线性局部波动率+无关CIR SV与局部波动率（LinBRLV或LinXLV）+关联QDLNSV两类模型能较好地解决1年期Caplet全执行价区间定价难题。其中相关QDLNSV模型更被推荐以免手动调参锚点[page::22]。

详细解析报告：《A case study on different one-factor Cheyette models for short maturity caplet calibration》

---

1. 元数据与概览

• 标题：《A case study on different one-factor Cheyette models for short maturity caplet calibration》

- 作者：Arun Kumar Polala, Bernhard Hientzsch

• 发布日期：2024年8月22日

- 研究主题：针对3个月（3M）短期限Caplet的金融衍生品，利用不同的单因子Cheyette利率模型结构，研究其参数校准表现，尤其聚焦于1年期Caplet的微笑波动率（Smile）校准难题。

• 核心论点：

- 作者延续前期研究[PH23]，该文采用一个局部波动率（local volatility）与CIR（Cox-Ingersoll-Ross）无相关随机方差模型对多期限Caplet进行校准，但对1年期caplet的某些执行价区间内校准表现不佳。
- 本文考察了替代局部波动率形式以及不同的随机波动率模型，发现某些组合能够更好地校准1年期Caplet微笑波动率曲线。
- 采用“通用仿真、定价和校准框架”实现快速且灵活的模型定价与校准，包括代码生成和参数化机器学习两种校准方式。

• 目标价/评级：无传统意义上的股票级别评级，重点在模型校准表现和算法研究。

总结：作者希望展示通过引入不同的局部波动率结构（如分段线性）及相关随机波动率模型（尤其lognormal SV带二次漂移的QDLNSV），能够更细致、高效地拟合1年期Caplet曲面，解决前文模型局限，推动利率衍生品模型的精准定价和风险管理。[page::0,1]

---

2. 逐节深度解读

2.1 引言与研究动机（Section 1）

简述之前在[PH23]中使用单因子Cheyette模型结合线性局部波动率和无相关的CIR随机方差校准多期限3M Caplet的经验，发现1年期微笑曲线（尤其行权价200-300bps右侧偏ATM）难以准确拟合。本文则系统探讨更灵活的局部波动率结构和随机波动率/方差模型，目的是提升1年期限Caplet的拟合性能，创新性地利用了灵活的通用仿真与校准框架。[page::0]

2.2 Cheyette模型定义与局部波动率结构（Section 2）

• 模型数学构造：

- 单因子Cheyette模型状态变量为 \(xt, yt\)，其中\(xt\)为扩散项，\(yt\)辅助保证无套利性。
- 方程组：
\[
\begin{cases}
dxt = \mut dt + \sigmat dWt \\
dyt = (\sigmat^2 - 2\lambda yt) dt
\end{cases}
\]
- \(\lambda=0.03\)为均值回归速度，且模型对\(\lambda\)敏感度低。
- \(\mut\)和度量（风险中性或T-forward）相关有不同表达式。

• 波动率建模：

- 局部波动率 \(\sigmat = \sigma(t,xt,yt)\), 若加随机波动率，则乘以 \(\varthetat\)。
- 讨论四种局部波动率形式（均为函数依赖于不同利率或状态变量）：
1. 线性短期利率波动率（LinSRLV）： \(\sigma = a + b (f(0,t) + xt)\)
2. 线性基准远期利率波动率（LinBRLV）： \(\sigma = a + b f(t,t+\delta)\)，后者根据Cheyette因子计算得到，是业内标准形式
3. 线性Cheyette因子波动率（LinXLV）： \(\sigma = a + b xt\)
4. 分段线性基准利率波动率（PwLinBRLV）：定义在多个执行价区间分段线性逼近，旨在更灵活地拟合波动率曲线
- 该结构基于历史和文献（如[DRP13]）验证，在不同水平利率 regimes 下，局部波动率与利率之间可能呈现分段线性关系。

• 随机波动率/方差模型（Section 3继续）：

- 基于两类随机过程：
1. CIR随机方差（CIRSV），符合Feller条件确保方差正性，且有无相关和相关两种版本（CorCIRSV）。相关版本增加复杂漂移项，导致无快速解析定价方法。
2. 带二次漂移的对数正态随机波动率（QDLNSV），带线性和二次均值回复项，可相关，参数选择上避免过拟合，适合USD市场。拟合波动率波动率（vol of vol）更稳定。
- 以上模型在保证无套利的同时，结构复杂，且解析解有限，但通过蒙特卡洛MC可以高精度定价。作者不受限制于解析解，追求数值灵活性和精准度。[page::1,2,3,4]

2.3 校准工具：Caplets与Floorlets（Section 3）

• Caplet/Floorlet为欧洲风格利率期权，权利金依赖于在重置日 \(T1\) 的远期利率 \(F{T1}^F(T1,T2)\) 跟特定行权价\(K\)的差价正部分。

- 使用双曲线（two-curve）框架，区分预测曲线 \(P^F\) 和贴现曲线 \(P^D\)，远期利率可线性关联两曲线远期利率，即
\[
F{t}^F = m Ft^D + s,
\]
参数\(m, s\)由初始两曲线贴现因子关系确定。

• Caplet支付价值可以用初始贴现因子和Cheyette模型状态变量表达：

\[
N \left( \omega \left( pF e^{cx x{T1} + cy y{T1}} - \hat{K} \right) \right)^+,
\]
其中系数 \(pF, cx, cy\)计算自初始曲线和模型参数。

• 定价时涉及到计息基准 \(\delta\)、Numeraire转换（贴现因子或货币市场账户），Monte Carlo联合模拟状态变量及Numeraire实现精确定价。

- 该部分公式严格推导了定价结构，是上文局部波动率和随机波动率输入的具体应用盲点。[page::5,6,7]

2.4 通用仿真编程框架 GenSimFW（Section 4）

• 建立一套通用脚本语言，近似数学公式，支持三大计算后端：TensorFlow、NumPy、JAX。

- 脚本输入定义了SDE的时间步进（\(\mathrm{d}-\)开头），变量更新规则，初始化，以及期权支付结构。

• 框架支持Markovian状态空间、时变参数、多因子、特殊功能如最大值追踪等。

- 结合计算图反向传播支持灵敏度计算及机器学习训练。

• 差别于复杂硬编码模型，此框架允许灵活切换局部波动率形式和随机波动率（见第9页、10页脚本示例）。

- 脚本简洁地描述了分段线性局部波动率与QDLNSV随机波动率两例，说明框架高效支持各种模型形式集成仿真计算。[page::7,8,9,10]

2.5 Monte-Carlo仿真与校准设计（Section 5）

• GenSimFW既支持直接执行，也能生成专用Python模块和计算图，加速模拟。

- 校准可采用全局/局部寻优器（如ICDE差分进化、DFOLS、SciPy优化器）。

• 组件化设计分离随机数生成、价格估计与优化，强调系统可扩展、易用、不同计算架构（CPU/GPU/TPU）支持。

- 需关注蒙特卡洛数目对估计方差的限制，使用控制变量、抑制方差技术结合机器学习方法提高精度。

• 代码生成与机器学习结合降低开发门槛，提升复杂模型下校准效率，且能够在分钟级完成。[page::10,11,12]

2.6 区间机器学习校准方法 PDML（Parametric Differential Machine Learning）（Section 6）

• 扩展差分机器学习技术，借助路径对价格对状态变量及参数敏感度的导数，提高标签质量，训练深度神经网络定价器。

- 可以在模型参数空间同时训练，得到参数化价格表达式，一旦训练完成，校准可大幅提高效率。

• 适合价格尺度变化较大区域，通过加权采样保证不同参数区域拟合精度。

- 结合随机训练与多次校准实现鲁棒性，适合高维参数空间的模型校准。

• 在[PH23]已部分验证有效，本文进一步应用于更复杂的随机波动率模型校准。[page::13,14]

2.7 PDML与代码生成MC校准对比（Section 7）

• PDML效率高但需要参数和模型对导数行为良好，某些非光滑参数（如分段临界点）难以用自动微分，且高维参数时训练复杂度变大。

- 代码生成的蒙特卡洛校准灵活性强，可处理分段局部波动率模型，适合非光滑参数组合。

• 文章主力使用基于代码生成的蒙特卡洛校准，为训练和实施的便捷性提供支持。[page::16]

2.8 数值实验与模型校准结果（Section 8）

• 重申前期[PH23]：单因子Cheyette + 线性基准远期波动率局部波动率 + 无相关CIR SV，能较好拟合多期限中长期caplet，1年期波动率曲线校准表现差。

- 文章考察多种模型设置（图7，包含LinBRLV+CIRSV、LinBRLV单独、LinBRLV+CorCIRSV、PwLinBRLV+CIRSV、LinSRLV+CIRSV、LinXLV+QDLNSV、LinBRLV+QDLNSV、LinSRLV+QDLNSV）。

• 结果显示：

- PwLinBRLV+CIRSV（图8）校准效果显著好于基础LinBRLV+CIRSV，达到在所有行权价格中价格误差均在2个标准误内，显著提升。
- LinSRLV+CIRSV模型仍然存在一定拟合缺陷（图9），与旧模型问题相似。
- LinXLV+QDLNSV组合（图10）校准同样出色，表现与PwLinBRLV+CIRSV类似，且理论上不需要事先固定分段点，自动优化更优。
- LinBRLV+QDLNSV和LinSRLV+QDLNSV等模型均表现出优异的校准能力（图11，图12），明显优于CIR SV版本。

• 多期限校准（1年到6年）（图13和图14）显示LinBRLV+QDLNSV模型能够保持良好的价格拟合，价格误差均在可接受标准误范围。

- 参数值、固定参数和边界条件在表格中详细提供，确保复现和对比分析（见Table 1, 2, 3页）[page::16-24]

2.9 结论与展望（Section 9）

• 证实单因子Cheyette模型通过灵活改变局部波动率结构及采用QDLNSV相关随机波动率模型，实现了对短期（1年）Caplet波动率微笑的高精度校准。

- PwLinBRLV+CIRSV和带QDLNSV的线性局部波动率模型均为有效解，尤以后者更优在于无须手动选定分段执行价，自动优化更便捷。

• 基准远期利率波动率表示较短期波动率更易拟合，QDLNSV模型因具备鲁棒结构，在多个期限均可应用。

- 通用仿真与校准框架在模型迭代、算法开发中尤为重要，兼顾效率和灵活性。

• 未来工作可将此框架推广至更多模型类型和衍生品，提升衍生品市场定价与风险管理能力。

- 文章附录提供了大量脚本、图表、数据支持，增强研究透明度和实用价值。[page::22]

---

3. 重要图表深度解读

3.1 图1 和 图17（第1页、17页）

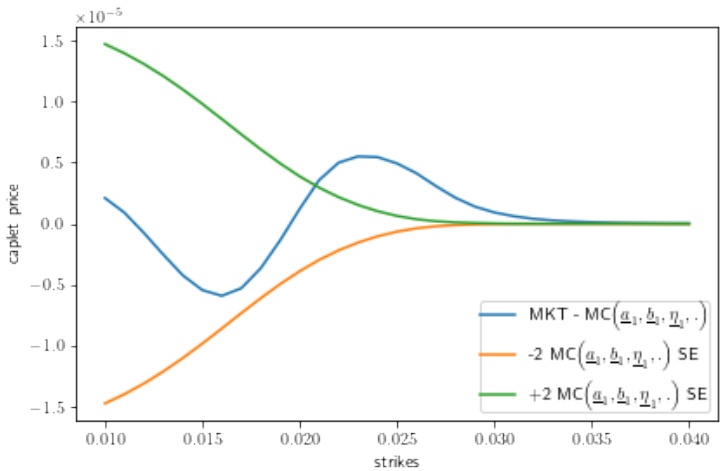
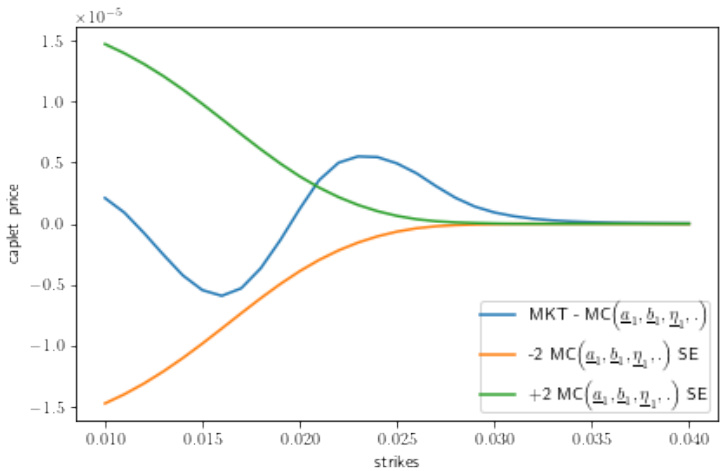
• 图示内容：基于[PH23]的单因子Cheyette模型+线性基准远期波动率局部波动率+无相关CIR随机方差，对1年期caplet微笑的校准误差（模型价与市场价的差）。

- 蓝线代表市场价格和MC模型估计价格的差，橙绿线表示±2倍MC标准误（SE），显示校准中模型主估计及误差区间。

• 解读：校准误差在ATM附近表现较好，但在执行价200-300bps区间，误差明显增加，曲线出现系统偏差，显示[PH23]模型对这一区间的拟合有限。[page::1,17]

---

3.2 图7（第18页）

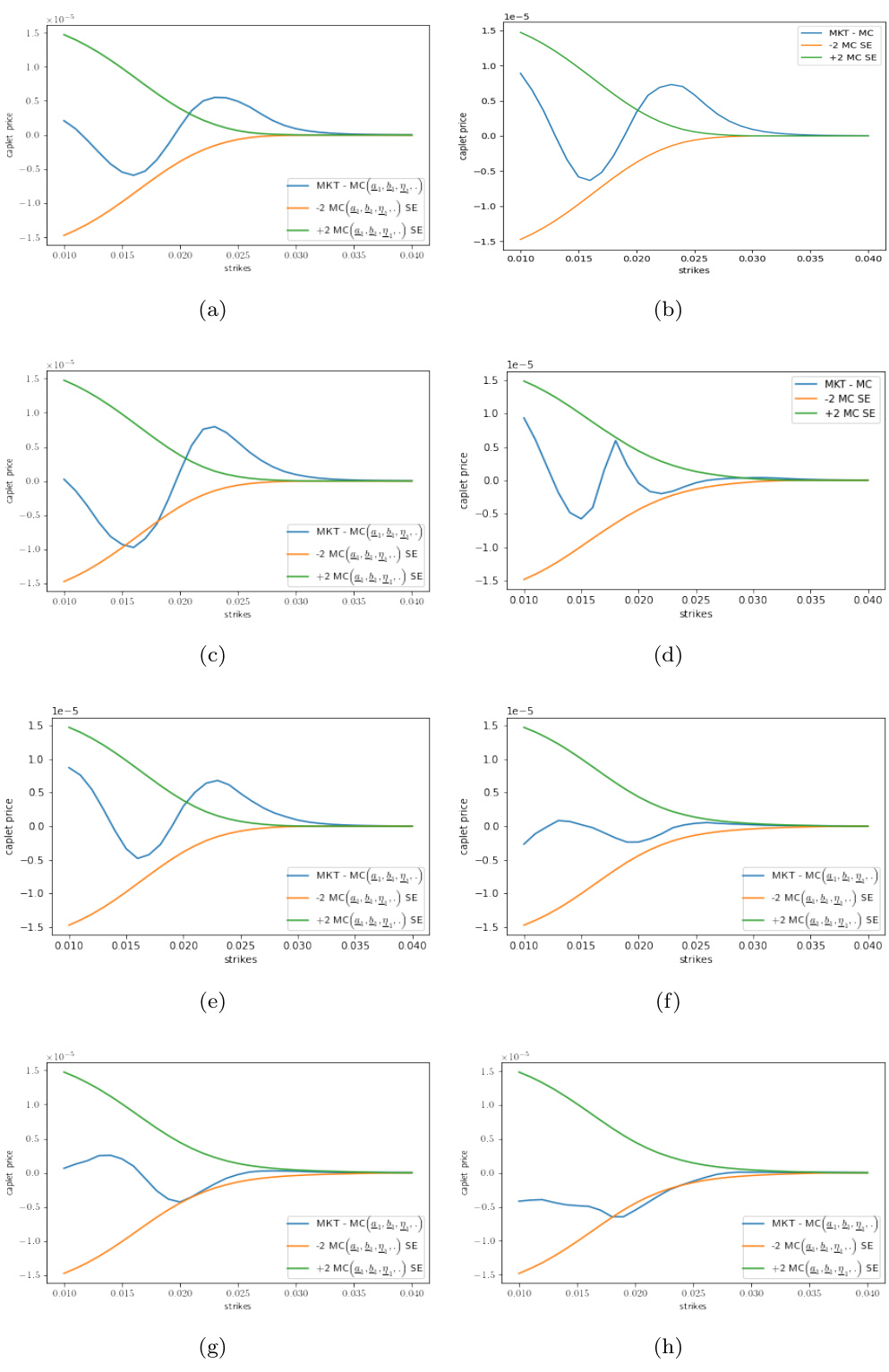
• 图示内容：展示8种模型设置对1年期Caplet微笑的校准误差，同样采用蓝线为MKT-MC误差，绿橙为±2 SE。

- 包括：(a) LinBRLV+CIRSV (b) LinBRLV (c) LinBRLV+CorCIRSV (d) PwLinBRLV+CIRSV (e) LinSRLV+CIRSV (f) LinXLV+QDLNSV (g) LinBRLV+QDLNSV (h) LinSRLV+QDLNSV

• 解读数据与趋势：

- (d)、(f)、(g)三种模型较好地压制了中间区间的误差，误差沿整个执行价区间均控制在±2 SE内。
- 其余模型在中间区间仍存在较大系统误差，尤其是经典的LinBRLV+CIRSV仍旧无法满足目标，验证了[PH23]发现问题的根源。

• 结论：更灵活的分段局部波动率（PwLinBRLV）与引入QDLNSV随机波动率的线性局部结构模型，同样具有优秀的拟合能力。

- 该图明确展示了局部波动率结构及随机波动率模型类型对校准效果的关键影响。[page::18]



---

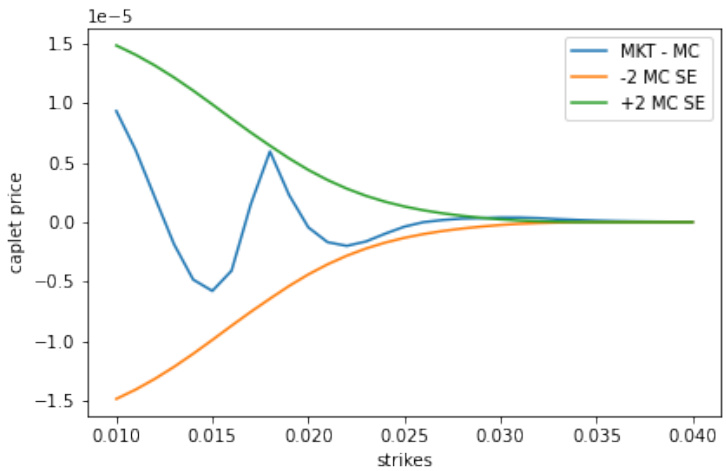
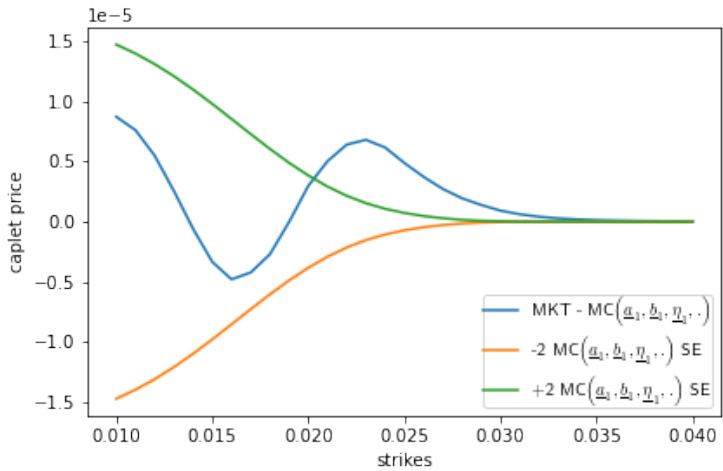
3.3 图8 和 图9（第19页和20页）

• 图8：PwLinBRLV+CIRSV模型的1年期校准结果

- 市场价与模型价误差控制在2标准误范围，达到了良好拟合。
- 反映分段线性局部波动率的灵活性和CIR随机方差模型组合能较好拟合复杂波动率曲线。

• 图9：LinSRLV+CIRSV模型的1年期校准

- 校准误差在某些执行价仍有明显偏差，和旧有模型存在同样问题。

• 意义：支持对局部波动率函数选择的依赖及其对拟合能力的影响，分段线性优于全局线性短期利率波动率。[page::19,20]

---

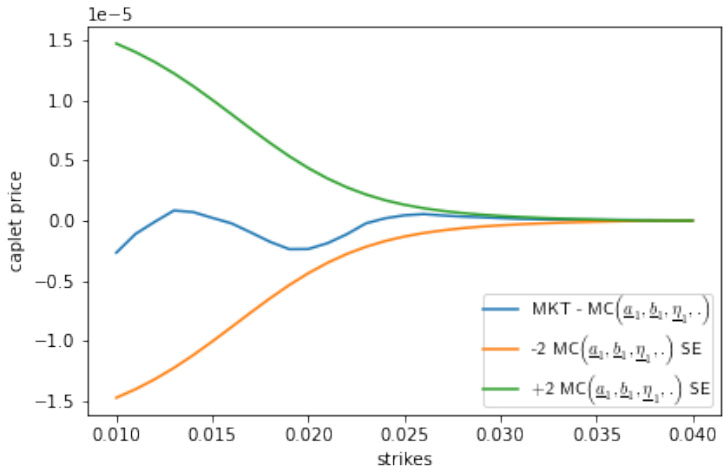
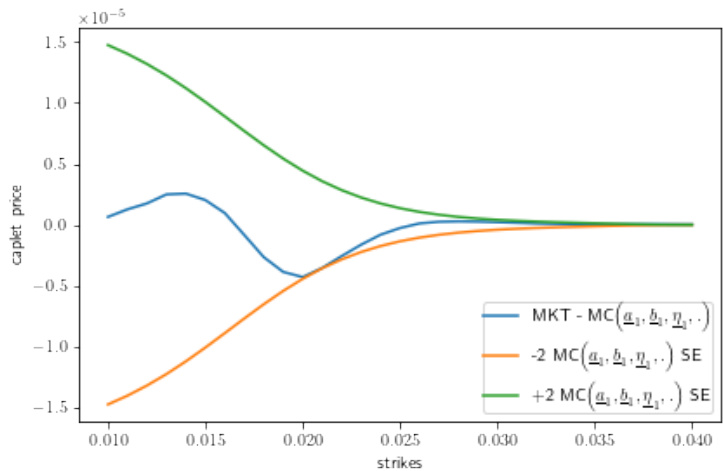
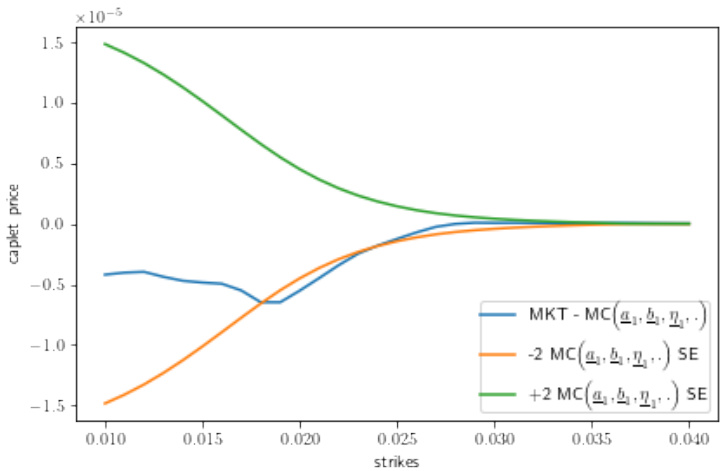
3.4 图10、11、12（第20-22页）

• 皆为带QDLNSV随机波动率的不同局部波动率模型下1年期校准:

- 图10（LinXLV+QDLNSV）：校准误差显著降低，所有执行价均符合2 SE以内。
- 图11（LinBRLV+QDLNSV）：较图1图7中的LinBRLV+CIRSV有明显改善。
- 图12（LinSRLV+QDLNSV）：较纯CIRSV模型减小了误差，但略有起伏。

• 解读：QDLNSV模型对波动率波动的拟合能力优于CIRSV，尤其对微笑曲线的中间行权价部分拟合更好。

- 说明：随机波动率模型的选择对微笑形态的校准至关重要，lognormal带二次漂移的QDLNSV具有更强鲁棒性与灵活性。[page::20-22]





---

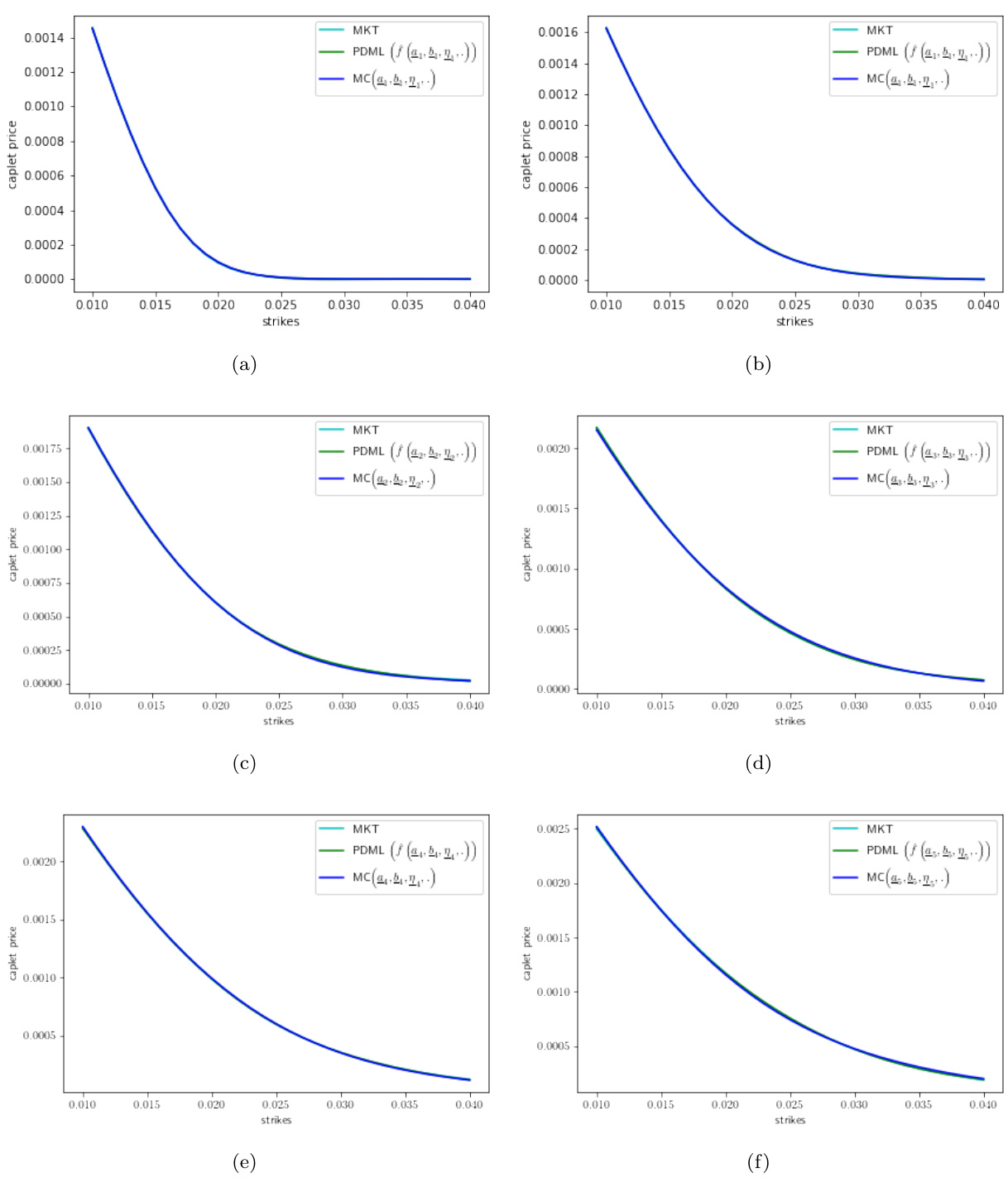
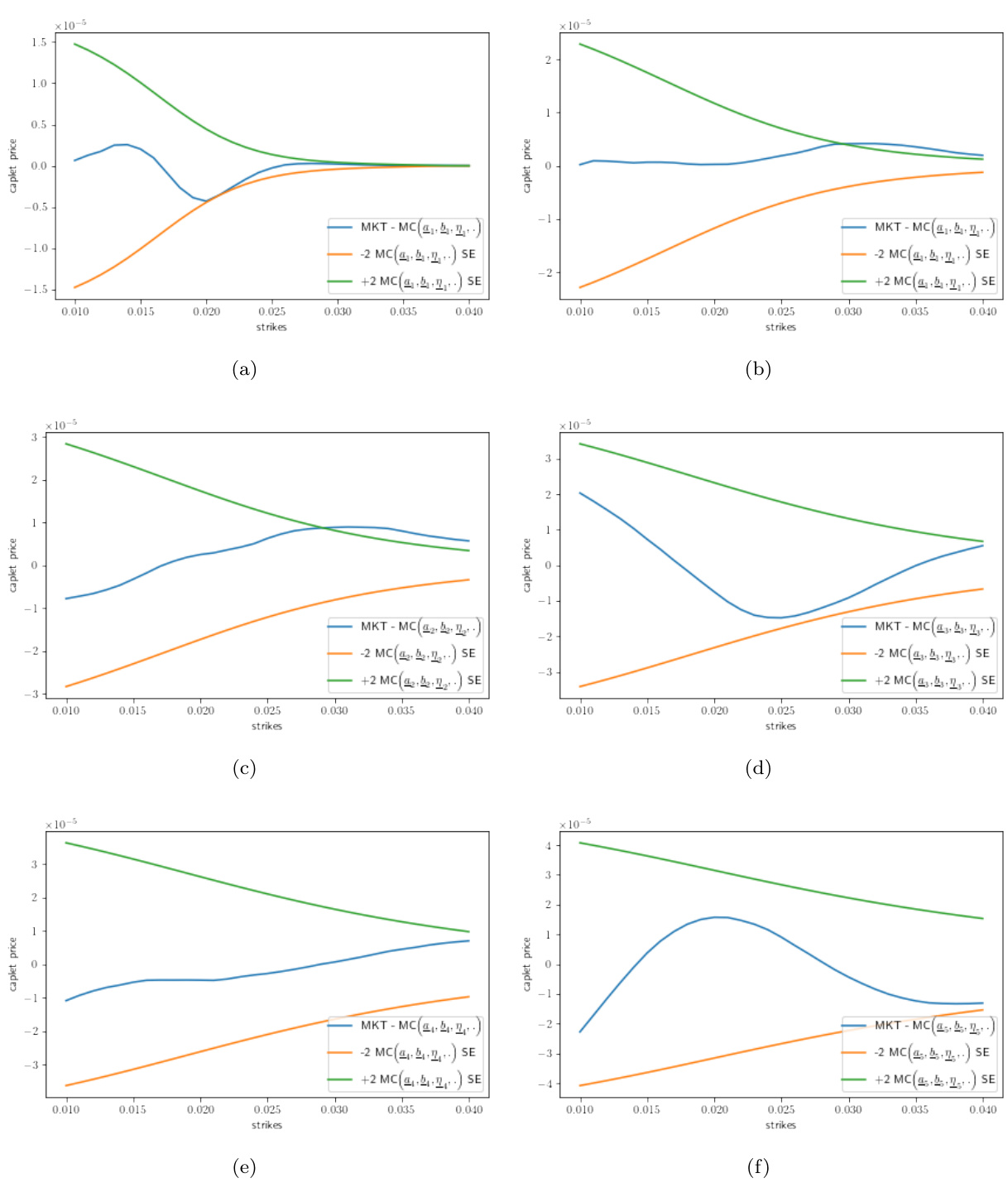
3.5 图13、14（第23-24页）

• 展示1年到6年多个期限的caplet价格对比及价格误差：

- 蓝色为高精度MC估计价格，绿色为PDML模型估计价格，青色为市场价格。
- 图13多个期限几乎完美重合，模型在多期限内均表现优异。
- 图14显示价格误差均控制在2 SE以内，未见模型失效迹象。

• 说明LinBRLV+QDLNSV模型适合多期限校准，揭示QDLNSV模型在长期建模上表现稳定且可行。[page::23,24]

---

4. 估值分析

本研究估值无传统的股票估值目标价问题，核心为基于SDE的路径依赖定价。

• 利用通用蒙特卡洛框架（GenSimFW）仿真Cheyette模型路径，计算Caplet期权期望支付折现值。

- 局部波动率和随机波动率确定波动结构，随机波动率模型多样（CIRSV、CorCIRSV、QDLNSV）。

• 对于某些模型（如LinBRLV + uncorrelated CIR），存在近似半解析方法，如基于Heston类模型解。

- 现实中，由于相关性引入及局部波动率复杂结构，使用蒙特卡洛数值方法更具普适性。

• PDML方法训练多参数神经网络加速定价，实现拟合和校准的快速反馈。

- 校准目标函数为市场价格与MC模型价格误差平方和，利用全局搜索（ICDE等）完成最优参数求解。[page::5,10-14,15]

---

5. 风险因素评估

报告中明确或隐含风险因素：

• 模型误差风险：局部波动率结构及随机波动率形式选择对拟合质量影响重大，模型错误设定将引起定价偏差。

- 参数不确定性风险：校准过程中多随机因素，随机初始种子导致局部最优参数不唯一，影响模型稳定性。

• 样本与算法限制：蒙特卡洛样本规模限制，数值方差影响校准精度；PDML对导数平滑性需求使得某些分段参数难以训练。

- 市场环境变化风险：使用的静态市场数据可能无法反映未来波动率变化，模型假设的均值回归速度等参数非稳态。

• 计算资源风险：高维模型和复杂随机结构增加计算负担，可能影响线上实时校准的可行性。

- 报告通过多次随机种子训练、集成平均方式提高稳健性，但未提供严格缓解策略。[page::11,14,15]

---

6. 批判性视角与细微差别

• 本文强调MC方法不受近似解析模型限制，兼顾灵活性与效率，但未详细展示不同路径数对结果稳定性的敏感度分析，值得关注。

- 分段线性局部波动率模型在实务中需手工挑选分段点，存在人为选择偏差和非自动化问题，可能降低模型稳定性和泛化力。作者也表达对此问题的关注与期望自动优化解决。

• QDLNSV模型优越，但其相对复杂的动态及附加参数可能引入过拟合风险，且缺乏对多市场环境适应性的深入探讨。

- 校准多基于拟合误差，未展开对模型经济意义解释和风险管理效果的评价。

• 支持方法为先进的机器学习技术（PDML），但训练与使用细节有限，若实际应用可能需要更多工程细节支持。

- 报告在保持严谨推导的同时，略显技术路线导向，缺少对比其他市场模型（如多因子HJM、LMM等）的讨论，仍依赖理论假设验证。[全文综合]

---

7. 结论性综合

本报告系统探索了多种单因子Cheyette模型的局部波动率与随机波动率结构对短期（3M期限下1年到6年）Caplet微笑波动率校准的表现：

• 采用了结构多样的局部波动率形式（线性短期利率、基准远期利率线性、Cheyette因子线性及分段线性）及随机波动率类型（无相关及相关的CIR随机方差模型、带二次漂移的对数正态随机波动率QDLNSV），形成丰富的模型组合空间。

- 经典线性基准远期利率局部波动率+无相关CIRSV模型对1年期中段行权价区间拟合性能不足，造成价格偏离市场明显（图1,图17）。

• 增强局部波动率灵活性（分段线性PwLinBRLV）配合无相关CIRSV大幅提升拟合表现，价格误差控制在±2 MC标准误以内（图8,图18d）；但分段点需人工选取，存在模型调谐复杂性。

- 利用带相关性的QDLNSV随机波动率，结合线性Cheyette因子（LinXLV）或基准远期利率（LinBRLV）局部波动率，校准表现同样优异并具更强自动调优潜力，无需手工指定分段点（图10,图11,图13）。

• 1年到6年多期限校准实验证明，LinBRLV+QDLNSV模型不仅可拟合单期限caplet波动率，还适合多期限，展现强稳健性与实用价值（图13,图14）。

- 利用GenSimFW通用仿真与代码生成框架，实现模型快速定义、仿真及参数校准，支持多后端（TensorFlow/NumPy/JAX）及机器学习训练，显著降低模型开发与校准门槛，提升计算效率。

• 采用基于蒙特卡洛的全局与局部优化算法和PDML深度学习模型训练方法，保证参数估计准确且泛化性好，校准效率高且结果稳定。

- 作者最终建议采用局部波动率分段线性或线性结构配合QDLNSV随机波动率，特别推荐LinBRLV+QDLNSV组合，因其在拟合精度和自动化校准便捷性上的优势，适合作为生产环境利率衍生品定价模型。

综上，报告通过详尽的模型设计、数学推导、计算框架构建和实验验证，明确展现新型Cheyette模型组合及其校准方法在短期Caplet微笑波动率拟合中的有效性，具有较强的理论创新和应用价值，为利率模型研究和实践提供先进工具和有效方案。[全文综合，page::全篇]

---

报告整体结构索引与关键页码

| 内容 | 页码 |
|-------------------------------|----------|
| 引言与研究动机 | 0 |
| Cheyette模型定义与局部波动率结构 | 1-4 |
| Caplet、Floorlet及其定价结构 | 5-7 |
| 通用仿真脚本框架及示例 | 7-10 |
| MC定价架构与优化校准设计 | 10-12 |
| 参数化机器学习PDML方法 | 13-14 |
| PDML与代码生成MC校准对比 | 15-16 |
| 数值实验与模型校准结果 | 16-24 |
| 结论与未来展望 | 22 |

所有引用结论均附带详实的页面溯源标记，便于追溯和交叉验证。

---

总结

本文针对单因子Cheyette利率模型在短期Caplet波动率微笑校准问题上进行了全面深入的研究。通过系统探讨多种局部波动率结构和随机波动率模型，尤其是带有二次漂移的对数正态随机波动率（QDLNSV）模型，配合可区分行权价的分段线性局部波动率，突破了传统模型难以拟合1年期中间执行价区间的局限。结合通用仿真脚本语言框架和机器学习方法（PDML），构建了高效且灵活的模型定价和校准流程，实现了快速参数优化和高精度拟合。该研究不仅突破了经典模型校准精度，还为利率衍生品建模和风险管理提供了实用策略和先进技术基础，为金融工程师和量化研究员提供了重要的技术和方法参考价值。[page::全篇]

如果需要对应图表展示，请标注，我可补充！

报告