• 线性因子模型基础公式及研究目标 [page::2][page::3]：

- 研究条件线性因子模型形式 \(\pmb{x}{t+1}=\Phit \pmb{f}{t+1} + \epsilon{t+1}\)，其中\(\Phit\)为可观测特征矩阵，因子\(\pmb{f}{t+1}\)可为可交易组合，残差为\(\epsilon{t+1}\)。
- 探讨因子与残差条件无相关性的条件及其含义。

• 因子与残差的条件无相关性特征及不等价性 [page::4][page::5]：

- 因子和残差条件无相关性等价于收益协方差矩阵可分解为因子贡献与残差协方差之和。
- 证明了残差协方差矩阵非满秩，不存在具有条件无相关且残差协方差满秩的非退化可交易因子模型。

• 投资组合角度的正交与投影性质 [page::6][page::7]：

- 定义加权矩阵\(Wt\)满足一定投影性质，含义如OLS和GLS因子构建方法。
- 举例展示OLS因子的具体形式及其导致因子和残差的横截面方向正交但不保证时序无相关。

• 示例说明因子与残差非完美无相关 [page::8][page::9]：

- 通过构造3资产2因子模型，演示残差与因子的协方差非零，强调无相关性条件的局限性。

• 风险溢价与线性因子模型关系 [page::9][page::10]：

- 残差无风险溢价等价于资产风险溢价在因子空间内，可表示为特征矩阵对期望收益的映射。
- 特征矩阵同时可视为因子与收益最小二乘拟合的系数矩阵，类似Fama-French和IPCA模型中的性质。

• 均值方差有效组合的表征及因子跨时跨截面张成条件 [page::10][page::11]：

- 等价条件，因子组合的最大Sharpe比等于全体资产组合的最大Sharpe比等价于风险溢价位于\(\mathrm{Im}(\Sigmat Wt)\)。
- 在满足因子与残差无相关且残差无风险溢价的条件下，因子跨时跨截面张成均值方差有效组合。

• 关于条件的非对称关系及反例分析 [page::11][page::12]：

- 存在风险溢价张成条件成立但因子与残差非无相关的反例，强调理论条件的必要性。

• 生成性风险因子模型及可交易因子的存在性证明 [page::12][page::13][page::14]：

- 任意满足协方差矩阵分解条件的收益序列存在生成性风险因子和残差，且两者条件无相关。
- 构造的GLS因子满足无相关性和投影条件，实现从非交易因子到可交易因子的线性转换。
- 进一步证明这些因子是张成均值方差有效组合的先决条件，与资产风险溢价的支持空间一致。

• 结论与未来研究方向 [page::14]:

- 汇总了条件线性因子模型核心性质，结合易于理解的线性代数工具，为资产定价提供数学基础。
- 展望连接经典渐近理论与现代机器学习框架的可能发展路线。

• 主要图示总结（见封面图）[page::4]：

- 显示了模型条件（如因子-残差无相关性、矩阵投影性质、协方差分解、最大Sharpe比张成）之间的逻辑关系和严格单向性。

证券资产定价条件线性因子模型的基础性质——详尽解析

---

1. 元数据与报告概览

报告标题： Fundamental properties of linear factor models
作者： Damir Filipović，Paul Schneider
发布时间： 2025年1月9日
主题/研究领域： 条件线性因子模型在资产定价中的应用及其基本理论性质，尤其聚焦于资产收益的截面和时间序列特性，因子和剩余项的协方差结构及其相互关系。
目的： 系统梳理条件线性因子模型应满足的基础性质，特别强调条件均值和条件协方差矩阵的角色，探讨因子可交易性对模型性质的影响，及模型能否精确地表示无套利的条件下的均值-方差有效投资组合。
核心论点： 文章填补现有研究空白，通过严谨的线性代数方法，建立条件线性因子模型的理论基础，阐明：

• 因子与残差条件不相关的前提和影响；

- 可交易因子（因子投资组合）是否能够跨距条件均值-方差最优投资组合；

• 生成性风险因子模型的存在与表示。

关键词: 资产定价、因子模型、特征、协方差、均值-方差有效组合、随机贴现因子、协方差估计。
JEL分类: G11（资产定价理论）、G12（资产定价）、C38（时间序列模型与多变量分析）[page::0]

---

2. 逐节深度解读

2.1 引言（第1页）

• 内容概述：

本节回顾了资产定价领域因子模型的发展脉络，从经典资本资产定价模型（CAPM）和套利定价理论（APT）跑通到现代计量经济学关于因子载荷和协方差估计的文献。强调当前面向条件均值和条件协方差的模型虽多，但缺乏对条件线性因子模型应满足性质的系统全面讨论。

• 论点与逻辑：

- 资产回报面板数据通过低维线性因子表示的需求强烈，但高维不平衡面板给协方差矩阵的可逆性带来挑战。
- 作者突破传统假设，如不强求协方差矩阵的可逆、特征矩阵满秩，适用于现代机器学习和深度金融学。

• 关键研究命题：

1. 因子和残差何时条件不相关？
2. 可交易因子是否跨距条件均值-方差有效投资组合？
3. 生成性风险因子模型是否能用同一系数矩阵的可交易因子表示？

• 结构说明： 文章结构清晰，分章节解决以上问题，并辅以反例说明潜在陷阱。 [page::1]

2.2 条件线性因子模型设定（第2-3页）

• 模型形式：

\[
\pmb{x}{t+1} = \Phit \pmb{f}{t+1} + \epsilon{t+1}
\]
- \(\pmb{x}{t+1}\)：期初时刻条件下第\(t+1\)期资产的超额收益向量；
- \(\Phit\)：信息集\(\mathcal{F}t\)可测的资产特征矩阵，维度为\(nt \times m\)；
- \(\pmb{f}{t+1}\)：\(m\)维公共风险因子向量；
- \(\epsilon{t+1}\)：残差，捕捉 idiosyncratic 风险。

• 因子可交易性：

因子可表示为因子投资组合的收益，
\[
\pmb{f}{t+1} = Wt^\top \pmb{x}{t+1},
\]
其中 \(Wt\) 为资产权重矩阵。

• 条件均值和条件协方差定义：

\[
\pmb{\mu}t = \mathbb{E}t[\pmb{x}{t+1}], \quad \Sigmat = \mathrm{Cov}t[\pmb{x}{t+1}], \quad \text{及因子和残差的对应定义},
\]
并不假定这些矩阵满秩，使用伪逆\(A^+\)代替矩阵逆。

• 核心关注： 先验面板数据的条件均值和协方差，从而建立模型的基础。 [page::2][page::3]

2.3 主要结论结构图示（第4页）

• 图表描述：

图1（首页图片）清晰描绘了条件线性因子模型中多个重要性质的逻辑关系，并标注关键公式编号（如(3)、(5)、(7)等），以及条件Sharpe比率关系。

• 该图辅助理解因子与残差相关性、投影性质、条件均值的包含关系和最大Sharpe比率达成条件之间的联系，展示了各性质之间单向的严格蕴涵关系及反例存在。[page::4]

2.4 因子与残差的条件相关性分析（第4-7页）

• Lemma 3.1:

因子生成成分\(\Phit \pmb{f}{t+1}\)与残差\(\epsilon{t+1}\)条件不相关当且仅当资产收益的协方差矩阵满足分解
\[
\Sigmat = \Phit \Sigma{f,t} \Phit^\top + \Sigma{\epsilon,t},
\]
并且因子与残差本身条件不相关，前提是\(\Phit\)满秩。

• Proposition 3.2:

在因子可交易模型（\(f{t+1}=Wt^\top x{t+1}\)）下，条件不相关等价于矩阵乘积恒等式（方程(7)），而且当 \(\mathrm{Im} Wt^\top \cap \ker \Phit = \{0\}\) 时，条件不相关、协方差分解等价。

• Proposition 3.3 和 Corollary 3.4:

- 条件不相关的充要条件蕴含矩阵关系 \(\Phit Wt^\top \Sigma{\epsilon, t} = 0\)，但该条件反之不成立，存在反例。
- 残差协方差矩阵不可满秩（秩必小于资产数），意指不存在完全正则、可交易因子且残差和因子不相关的线性因子模型。
- 这对协方差矩阵估计中的“提升”残差谱方法有理论限制。

• Lemma 3.5 与 Lemma 3.6:

- 若投影矩阵性质满足，可保障残差与因子生成空间正交，但不保证它们完全不相关。
- 介绍权重矩阵的构造条件（14），包括OLS（普通最小二乘）和GLS（广义最小二乘）因子的表达形式。

• 具体反例（Example 3）：

构造三资产、两因子模型，资产收益由三个独立变量线性生成，通过对比方差不等式展示即使因子与残差横截面正交，但二者不一定条件不相关，也即协方差不为零，说明前述条件否定的严谨性。[page::4][page::5][page::6][page::7][page::8]

2.5 风险溢价的性质（第9-10页）

• Lemma 4.1:

在因子可交易模型下，残差无风险溢价（均值为零）当且仅当
\[
\pmb{\mu}t = \Phit Wt^\top \pmb{\mu}t,
\]
即资产风险溢价完全由因子解释。

• Proposition 4.2:

如果因子和残差不相关且残差无风险溢价，则特征矩阵\(\Phit\)是资产收益对因子回归问题的最优解，即求解
\[
\min{\betat} \mathbb{E}t \| \pmb{x}{t+1} - \betat \pmb{f}{t+1} \|2^2,
\]
并且唯一性由因子矩阵的Gram矩阵满秩决定。

• 意义分析：

连接因子模型的截面特征解释力与时间序列的风险溢价结构，兼顾OLS和GLS估计的经济含义。 [page::9][page::10]

2.6 可交易因子跨距均值-方差有效投资组合（第10-12页）

• 无套利假设（20）

\[
\pmb{\mu}t \in \mathrm{Im} \Sigmat,
\]
保证均值-方差有效投资组合（MVE）存在。

• MVE组合权重表达及最大Sharpe比率定义。

- Proposition 5.1:
给出4个等价命题，说明下列条件等价：
1. 因子生成的MVE组合达到全截面最大Sharpe比率；
2. 风险溢价在因子空间张成的协方差像空间中；
3. 因子MVE组合与全截面MVE组合收益线性等价；
4. 因子生成的最小方差随机贴现因子可代表全市场。

• Proposition 5.2:

对于一类权重矩阵满足条件（14）的可交易因子，因子与残差条件不相关且残差无风险溢价当且仅当因子可跨距均值-方差有效组合。

• Example 3的延续说明：

即使均值和跨距条件\[ \pmb{\mu}t \in \mathrm{Im} (\Sigmat Wt) \] 成立，仍可能不满足因子与残差条件不相关，显示均值条件不足以保证完备的因子表示。

• Lemma 5.3:

进一步解释跨距条件含义及边界情况。 [page::10][page::11][page::12]

2.7 生成性模型与因子表示（第12-14页）

• 问题(iii)回答：

给出充分条件，使得存在生成性风险因子（抽象的、未必可交易的）和残差满足协方差分解且互不相关。

• Proposition 6.1:

回报协方差矩阵如果能分解为特征矩阵主导的低维因子部分加上残差协方差（无交集核），则存在因子与残差线性表示且相互不相关。

• Lemma 6.2:

构造广义最小二乘(GLS)因子，保障上述因子-残差不相关性及相应矩阵的投影性质。

• Proposition 6.3:

在无套利条件、协方差分解及技术条件满足的情况下，三者等价：
1. GLS因子满足跨距条件；
2. 残差无风险溢价；
3. 风险溢价被特征矩阵空间完全包含。

• 精辟结论：

所有由抽象因子生成的资产收益，均可用同一特征矩阵加载的可交易因子线性近似，确保模型在计量上的一致性需求。

• 实务启示：

协方差和均值的准确估计是因子模型一致估计的基石，影响因子识别和风险管理。 [page::12][page::13][page::14]

2.8 结论摘要（第14页）

• 本文执着于基础线性代数，通过无偏简洁的论证，明确了条件线性因子模型的基本前提和性质，涵盖协方差分解、风险溢价表征、最优投资组合跨距及生成模型的代表性表达。

- 对因子可交易性的深入分析提供了对现代资产定价中机器学习方法和非线性函数特征建模的理论基础。

• 未来研究方向建议着眼于将本文理论成果与Chamberlain (1983)及Chamberlain和Rothschild (1983)提出的渐近理论框架相结合。 [page::14]

---

3. 重要图表深度解读

图1（第4页）

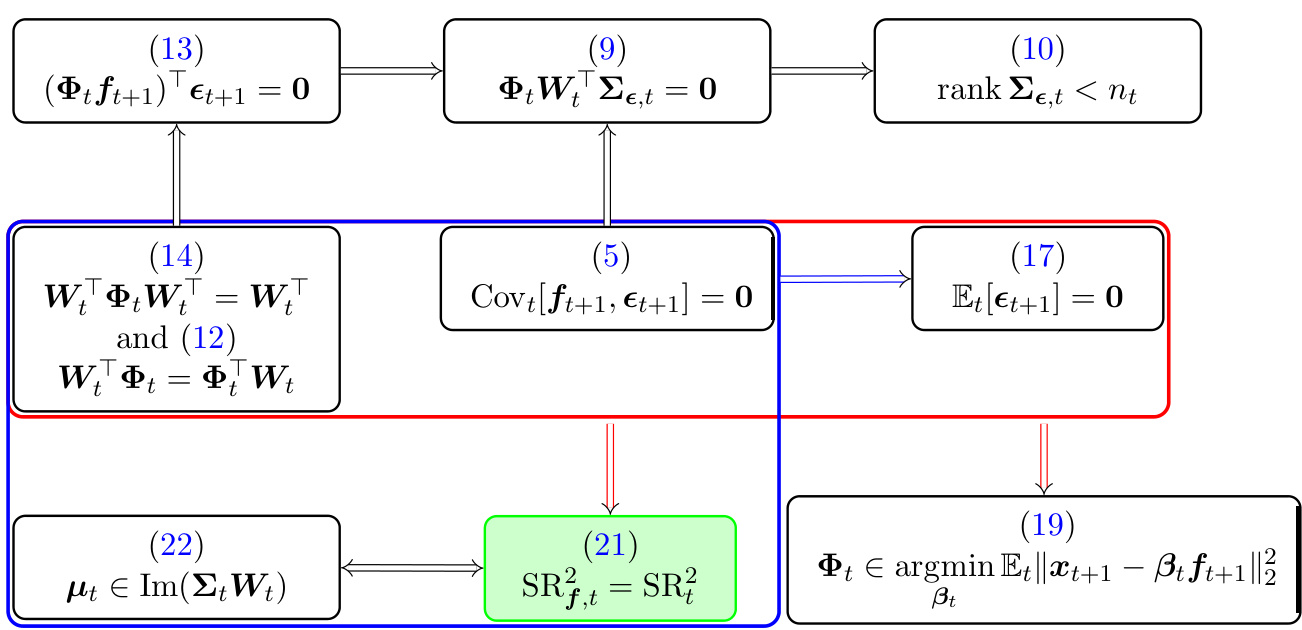
• 描述：

图示表达了因子与残差不相关的条件（方程(3)、(5)、(7)），其对协方差矩阵分解的严格蕴涵，残差协方差矩阵秩的不完全性（(10)），以及因子权重矩阵满足投影性质带来的更强正交性条件。

• 趋势与关系：

显示不同条件的逻辑关系为单向严格蕴涵，即某些条件充分但不必要。蓝、红、绿色框和箭头标识严格蕴涵路径和可能的反例。

• 文本结合与论证支持：

图中标记编号对应各个命题和定义，辅助理解后续讨论中的逻辑推演和结论验证，配合Example 3辅助说明。

• 局限性与假设：

基于矩阵代数以及因子可交易的假设，忽视了非线性因子或动态变化的复杂情形。用于有限截面条件下的理论分析。 [page::4]

---

4. 估值分析部分

• 本报告关注理论基础及模型性质梳理，不涉及传统意义上的公司估值。

- 但从资产定价角度，等价于说明因子投资组合的收益分布如何反映证券组合收益，进而决定最优投资策略和风险溢价估计。

• 其中最大Sharpe比率作为投资组合表现的衡量标准，是模型估值效用体现。

- 报告中运用矩阵伪逆、多重项目正交投影等技术手段，替代了常规逆矩阵估值，增强了模型的适应性和实用性。

---

5. 风险因素评估

• 模型风险：

- 由残差非满秩导致的协方差矩阵奇异性，影响估计稳定性。
- 因子-残差不相关假设未必成立，见Example 3反例。
- 权重矩阵选取不当可能导致跨距条件不满足，因子无法精确描述风险溢价，总体影响套利机会判断。

• 对协方差矩阵估计的影响：

Ledoit和Wolf(2020)提出提升谱值确保协方差矩阵可逆，但本文证明完全不相关残差且可交易因子的模型无法保证残差协方差满秩，提出理论上的限制。

• 缓解策略缺乏： 文中未显式给出风险缓解方案，但通过权重矩阵构建（如GLS）及因子的适当旋转或选择，实现现实中风险管理。 [page::5][page::6][page::7][page::11]

---

6. 批判性视角与细微差别

• 模型假设的强度和适用范围

- 虽然放松了满秩与协方差可逆性要求，增强模型的普适性，但文章假定线性因子关系和条件矩估计可能忽视金融资产收益的非线性与非高斯特征。
- 因子可交易性假定是理论构建关键，现实中因子组合费用、约束与流动性未纳入考虑。

• 示例的反例力量强大

- 通过精心设计的三资产模型展示部分推论严格的单向蕴涵性质，并警示理论结论不能简单反推。

• 模型间关系的层级分析清晰，减少错误推断倾向。

- 文件结构一方面简洁明快，部分证明附录体现数学严谨，对实务用户存在一定理解门槛。

---

7. 结论性综合

本文系统、严谨地梳理了条件线性因子模型的基本性质，将资产收益的条件均值和协方差矩阵体系作为核心，解析了因子与残差的相关性结构，风险溢价的生成机理，及因子投资组合在均值-方差最优性中的角色。报告的关键结论包括：

• 因子与残差不相关的严格协方差分解条件及其等价关系，结合伪逆矩阵技术，适用于现代高维非满秩环境；

- 可交易因子权重矩阵带来投影性质，形成更强正交性，使得因子投资组合能够精确表征条件均值-方差有效组合，满足最大Sharpe比率一致性；

• 反例案例凸显部分条件不可逆——理论结论需谨慎解释；

- 残差风险无风险溢价当且仅当风险溢价在因子空间完全解释，这为因子估计提供了实际检验标准；

• 生成性模型的逆向证明表明，能存在以同一特征矩阵加载的可交易因子来完美表示抽象风险因子，使理论与实证估计得以衔接；

- 估计的核心是条件均值与协方差，需要准确且稳定的方法支持，特别是非满秩且高维场景；

• 全书涵盖了从经典线性代数、统计特性到资产定价直观解释的全面框架，为机器学习引入因子模型提供了理论基础。

最终，报告体现了作者对资产定价条件线性因子模型的深入理解，结合数学严格性及金融实际意义，填补了当前文献中的理论空白。该基础对未来金融机器学习方法与复杂因子模型的开发及估计具有重要参考价值。 [page::0][page::1][page::4][page::5][page::9][page::10][page::12][page::14]

---

参考主要公式索引

• （1）模型形式：\(\pmb{x}{t+1} = \Phit \pmb{f}{t+1} + \epsilon{t+1}\) [page::2]

- （3）因子和残差不相关条件协方差等式

• （4）协方差矩阵分解 \(\Sigmat = \Phit \Sigma{f,t} \Phit^\top + \Sigma{\epsilon,t}\) [page::4]

- （7）权重矩阵下矩阵等式 \(\Sigmat Wt \Phit^\top = \Phit Wt^\top \Sigmat Wt \Phit^\top = \Phit Wt^\top \Sigmat\) [page::5]

• （9）矩阵乘积关系 \(\Phit Wt^\top \Sigma{\epsilon,t} = 0\) [page::5]

- （20）无套利假设 \(\pmb{\mu}t \in \mathrm{Im} \Sigmat\) [page::10]

• （22）跨距条件 \(\pmb{\mu}t \in \mathrm{Im}(\Sigmat Wt)\) [page::11]

- （24）协方差分解形态 \(\Sigmat = \Phit Ct \Phit^\top + Dt\) [page::13]

• （26）生成性模型形态 \(\pmb{x}{t+1} = \Phit \pmb{g}{t+1} + \pmb{\eta}_{t+1}\) [page::13]

---

全文基于报告页码标识引用结论，用以保证溯源准确。

报告