• 研究背景与问题描述：

- 随机投资组合理论（SPT）关注生成几乎必然超越基准投资组合的投资策略，即相对套利[page::0][page::1]。
- 最优套利问题等价于求半线性抛物型Cauchy偏微分方程的最小非负连续解，该PDE在高维时解析求解困难，且解不唯一，增加了数值求解难度[page::0][page::3][page::4]。

• 市场模型与数学基础：

- 设定包含n个股票的市场，股票价格服从由n个独立布朗运动驱动的随机微分方程。市场组合权重定义为各股票市值占比，财富动态由投资策略决定[page::1][page::2]。
- 给出相对套利严格定义及最优套利初始资本的数学表达式，系统性描述了问题的概率和PDE框架[page::2][page::3]。

• 波动率稳定市场（VSM）模型与贝塞尔过程的应用：

- VSM模型中股票资本服从特定随机微分方程，市值演变与贝塞尔过程紧密相关，可通过时间变换将其表示为贝塞尔过程[page::4][page::5]。
- 建立了将原高维PDE问题转化为对时间变换后的贝塞尔桥过程的模拟，解决了直接离散化导致的数值溢出和精度丢失问题[page::5][page::6]。

• 数值算法设计与实现：

- 设计蒙特卡洛模拟算法，基于时间变换贝塞尔过程生成资本路径，利用分段插值（线性及贝塞尔桥插值）获得期末状态，计算最优套利函数值[page::5][page::6]。
- 实验展示了不同股票数量下的最优套利估计，发现当初始资本较小时，结果存在数值不稳定，贝塞尔桥插值及高阶SDE数值方法如Milstein法有助改善稳定性[page::7][page::8]。

• 量化因子构建与策略总结：

- 主要量化结构为最优套利函数u，与股票资本乘积和市值比值相关，同时包含指数衰减项。PDE解对应投资策略的最低初始资本[page::4][page::7]。
- 数值方法能够捕捉到潜在的边界行为（股票资本趋近零的轨迹），揭示多解特性及市场中套利机会的存在性[page::7][page::8]。

• 反射型后向随机微分方程（BSDE）通用方法：

- 讨论通过反射型BSDE处理半线性Cauchy PDE非负最小解的障碍问题，将PDE求解问题转化为带障碍反射条件的BSDE的最小解，便于数值逼近[page::8][page::9][page::10]。
- 该方法为后续对非波动率稳定市场、投资者互动等复杂模型提供了理论计算基础[page::10]。

• 结论与展望：

- 论文突破高维PDE数值求解瓶颈，提出基于贝塞尔桥的时间变换蒙特卡洛算法，实现了相对套利最优策略估计，展示数值稳定性与准确性[page::5][page::7][page::10]。
- 未来可结合深度学习方法及有限差分方法，拓展至具有多重解的复杂金融模型及均场博弈框架，为金融量化研究提供新思路[page::10]。

深度分析报告：《Finding the nonnegative minimal solutions of Cauchy PDEs in a volatility-stabilized market》

---

1. 元数据与概览

• 报告标题：《Finding the nonnegative minimal solutions of Cauchy PDEs in a volatility-stabilized market》

- 作者：Nicole Tianjiao Yang、Tomoyuki Ichiba

• 主题领域：随机投资组合理论（Stochastic Portfolio Theory, SPT）、最优套利、偏微分方程（PDE）数值解、波动率稳定市场模型

- 发布时间：（报告未明确标注出版时间，根据引用文献2023年底之前）

• 核心论点：

- 目标是通过求解与最优相对套利（optimal relative arbitrage）相关的Cauchy类型偏微分方程（PDE）寻找其非负的最小解。
- 该类PDE存在多解性，高维且求解难度大。
- 在波动率稳定市市场模型中，利用时间变换的贝塞尔过程（Bessel bridges）构造数值算法求解该PDE。
- 提出算法并用数值实验验证其在实际市场模型下的有效性。

• 作者传达的关键信息：

- 最优相对套利的数学本质是Cauchy问题的非负最小解。
- 传统的网格法求解高维PDE面临维数灾难等问题。
- 将股本资本量化为时间变换的贝塞尔过程，有助避免数值溢出和零崩溃问题。
- 通过模拟和插值方法有效计算数值解。
[page::0,1]

---

2. 逐节深度解读

2.1 引言与问题背景（第0页）

• 总结关键点：

- 相对套利定义：构造能几乎确定超越基准组合的策略。
- 最高的相对收益对应于一个特定的PDE的非负最小连续解。
- PDE的非唯一性和高维度导致求解难度。
- 市场不假设不存在套利机会。
- 传统数值方法在此类问题中受限。

• 推理依据：

- 引用Fernholz等文献定义SPT和相对套利，表明市场存在套利机会是允许的。
- 代表性市场模型包含波动率稳定模型，适合理论与实践结合研究。
- PDE多解情况关联于金融不确定性资产价格模型和泡沫现象。

• 重要数据与术语说明：

- “强相对套利”是几乎确定胜过市场的策略。
- PDE非唯一解是该理论的核心难点，数学和数值分析双重挑战。

• 核心概念解释：

- 波动率稳定市场模型意味着股价波动率与市值水平相关联，体现现实市场中的“杠杆效应”。
[page::0]

2.2 市场模型构建（第1-2页）

• 关键论点：

- 设定了包含n个股票的市场模型，股价由n维布朗运动驱动。
- 股本资本（capitalization）符合随机微分方程，有可逆的波动率矩阵，市场为完备市场。
- 投资策略定义为可度量的进程，且财富动态遵循自融资规则。
- 市场组合定义为按市值加权的组合。
- 最优套利的定义基于找到最小初始资金量使投资组合最终至少等于市场组合。

• 推理与假设：

- 假设独立布朗运动，避免不必要的相关性，保证市场模型充分随机多样。
- 定义投资策略在可积性条件下，保证财富过程良好定义。
- 通过最优套利定义表明投资者希望以最小启动资本在终点超越市场。

• 关键等式及意义：

- 股价动态SDE（2.1）：描述股价演化。
- 投资组合空间Δn定义，体现权重总和为1。
- 投资者财富动态（2.5）建立策略对应财富的数学联系。
- 最优套利u(T)的数学定义（2.7）关键阐述目标成本。

• 细节说明：

- 资本总和X(t)的显式定义以及市值组合π^m的构造。
- 市场价格风险过程θ的定义及其重要性。

• 核心概念解释：

- 本节扎实搭建了后续基于市场价格过程的PDE求解问题的数学基础。
[page::1,2]

2.3 最优套利的PDE特征与数值挑战（第3页）

• 章节重点：

- 最优套利量u(t,x)满足的偏微分方程及其初值条件。
- PDE为半线性抛物型且无显式解。
- 网格法数值求解面临高维性难题和多解选择问题。
- 引出波动率稳定市场模型作为研究对象。

• 动机与依据：

- 基于[9]的理论结果，u是Cauchy PDE的非负最小解。
- 传统算法难以处理问题，故探求基于贝塞尔过程的数值方法。

• 数学模型摘要：

- PDE（3.1）：主方程与初值给定，显示与市场协方差矩阵aij相关。

• 概念说明：

- 存在非唯一性意味着解决方法需选择“最小非负解”。
- 贝塞尔过程与市值过程的联系为后续算法提供理论支撑。
[page::3]

2.4 波动率稳定市场模型（第4页）

• 章节核心：

- 定义VSM市场中资本动态，股价方差依赖于自身和总体资本。
- 利用Bessel过程建模资本的时间变换过程。
- 明确关键SDE与对应的参数范围（κ ∈[1/2, 1]）。

• 信息解读：

- 波动率稳定模型中每个资产依赖市场整体资本X(t)，体现资本之间的耦合。
- 定义方差结构为对角矩阵，简化耦合。

• 关键定义：

- Bessel过程定义，及其从平方过程Qt到Bessel过程Rt的关系。
- 资本过程表达成时间变换的平方Bessel过程，简化数值模拟。

• 推断：

- 采用时间变换的Bessel过程模仿市场资本动态，提高数值稳定性。

• 等式说明：

- 最优套利表示式（3.5）给出通过条件期望计算最优套利u的具体表达。
[page::4]

2.5 数值解法与模拟方法（第5-6页）

• 数值解法描述：

- 通过时间变化映射\(\Lambda(t)\)定义随机时钟实现资本过程的时间变换。
- 利用反转随机时钟\(\Lambda^{-1}(t)\)，处理资本过程的离散化。
- 模拟 \(n\) 个独立Bessel过程及其平方作为时间变换后的资本值。

• 算法步骤解读：

- 离散时间网格设定及对应的反时钟映射采用累加方式表达。
- 使用蒙特卡罗（Monte Carlo）方法采样足够多路径进行条件期望估计。
- 线性插值和更精细的Bessel桥插值方法用于获取非均匀时间点的资本值。

• 公式重点：

- 公式3.8和3.9是贝塞尔过程的关键演进与时间变换本质。
- 插值式（3.10）和Bessel桥过程的SDE公式表示细化数值路径。

• 数值算法总结（Algorithm 3.1）：

- 核心为基于时间变换的Bessel过程模拟，结合插值方法完成最优套利量求解。
- 定义输入参数（资产数量、Bessel维数、网格密度、蒙特卡罗路径数）。
- 充分体现了Markov性质，确保条件期望估计准确。

• 算法实用性：

- 对高维系统做出数值可行的解决方案。
- 通过贝塞尔过程的特性减轻零边界问题和数值溢出。
[page::5,6]

2.6 数值实验与结果展示（第7-8页）

• 实验设定：

- 固定终点时间 \(T=1\) ，时间步长 \(\Delta t=0.01\)，模拟路径数1000。
- 比较考虑两个股票和八个股票的资本初值空间。
- 采用线性插值和贝塞尔桥插值方法对不均匀时间网格数据插值。

• 观测与解读：

- 图1中，随着资本初值变小，数值结果不稳定，体现了传统方法的问题。
- 贝塞尔桥插值提升了数值稳定性并且更精确。
- 红色和蓝色轨迹在辅助过程\(\zeta{i}(t)\)上的表现表明系统可能触碰边界，体现相对套利中边界效应的重要性。

• 从图像分析：

- 3D图展示了最优套利量与资本初值和时间的关系，表明套利量随时间推进不断增加，趋向1（意味着达到盈亏平衡）。
- 随着其他股票资本设置提升，整体套利值有所变动，体现高维影响。

• 理论与数值呼应：

- 根据[9]和[15]，辅助过程触及边界对应套利存在的潜在风险和机会。
- 图2显示结果符合该理论框架。

• 公式阐释：

- 为更广泛的VSM引入参数 \(\zeta \in [0,1]\)，公式指出更一般化的最优套利表达，结合衰减系数体现市场风险修正。
[page::7,8]

2.7 反射型背向随机微分方程（BSDE）方法（第8-10页）

• 方法引入：

- 为解决PDE的非负最小解问题，提出用障碍（obstacle）问题对应的反射型BSDE求解。
- 障碍问题包含PDE和限制条件（例如函数须不低于某一界限）。

• 数学定理与命题：

- 根据Proposition 4.1，解PDE的最小非负解对应满足特定BSDE系统的过程。
- 明确了PDE解析解与BSDE路径依赖解之间的桥梁。

• BSDE构造：

- 构造BSDE系统（4.3）和带障碍约束的反射BSDE（4.5）形式。
- 补充过程\(K{t}\)保证解满足障碍限制，是非负解的“最小推动”。

• 方法优势：

- 反射BSDE提供了处理多解且保持非负的有效数学工具。
- 以概率方式间接求解无法显解的PDE。

• 技术细节：

- 利用Itô公式联系PDE偏导与随机过程演化。
- 可用惩罚法逼近反射BSDE，便于计算实现。

• 链接：

- 反射BSDE与最优相对套利的PDE问题建立联系，为求解非负最小解提供了理论基础和数值思路。
[page::8,9,10]

2.8 讨论与未来方向（第10页）

• 总结陈述：

- 研究提供了在波动率稳定模型下非负最小解PDE问题的数值概率解法。
- 使用时间变换Bessel过程有效地完成了PDE最优套利量的数值逼近。
- 实验中体现了算法的稳定性及现实市场模型的适用性。

• 拓展方向：

- 研究多投资者交互模型，涉及随机微分游戏理论。
- 可能采用多维正向-反向PDE联立方程数值方法。
- 期望借助深度学习方法解决多解情况下高维PDE的计算难题。

• 文献支持：

- 列举相关数值PDE求解和BSDE理论文献，丰富了学术背景。

• 关键点：

- 确认非唯一性PDE的研究对金融数学和投资组合理论的重要性。
- 提供了概率和数值结合的多维方法论。
[page::10]

---

3. 重要图表深度解读

图1（第7页）

• 描述：

- 展示不同资产数量（2和8）下的最优套利量 \(u(T,x)\) 在初始资本区间为[3.5, 9]²内的数值表现及时间演化曲线。
- 4个子图分别体现二维和八维市场配置下的算法表现。

• 数据解读：

- 图(a),(c),(d)为3D曲面，显示 \(u\) 对于不同初始资本的敏感度。
- 图(b)呈现时间轴上 \(u\) 的演变，带有置信区间，表现平滑增长特性。
- 小资本初值会导致数值结果不稳定（如(c)与(d)对比）。

• 联系文本：

- 支持对传统网格法和直接欧拉模拟的挑战论述。
- 也印证了通过贝塞尔过程模拟的优势。

• 局限性：

- 由于维数增加，数值不稳定性依然存在，提示需更高效插值及模拟技术。

• 图片参考：

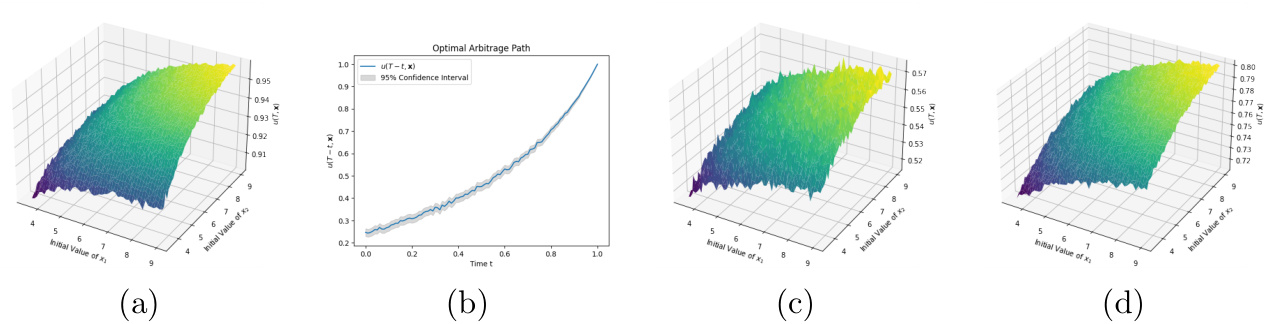
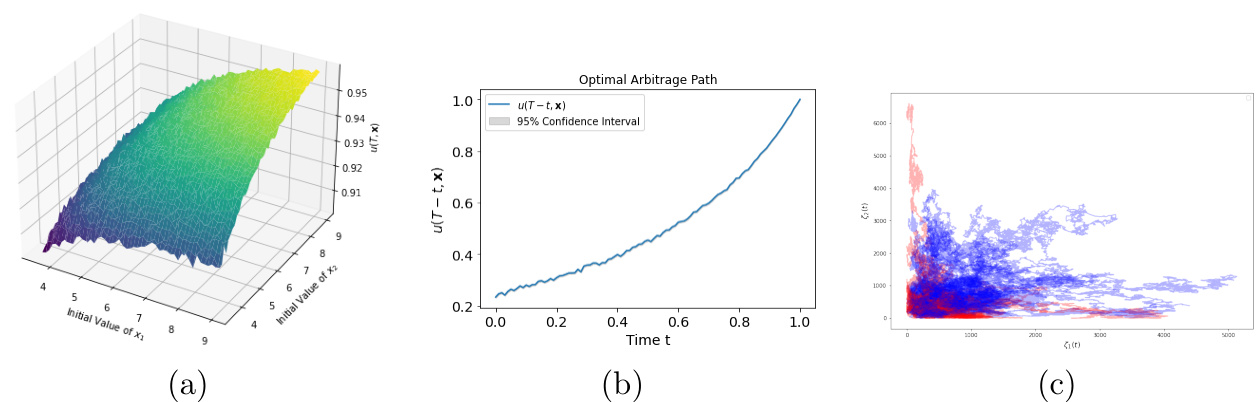
图2（第8页）

• 描述：

- 使用贝塞尔桥插值方法，二维资本空间上 \(u\) 的分布与时间演变。
- 演示两维辅助过程轨迹是否触及零边界。

• 数据分析：

- 图(a)中 \(u\) 曲面更平滑，数值稳定性提升。
- 图(b)回顾时间路径，稳健展示整体回报增长。
- 图(c)辅助过程轨迹中红色轨迹碰到边界位置，表明部分路径触发套利边界限制。

• 文本联系：

- 佐证反射BSDE中障碍约束条件的市场表现。
- 体现套利存在边界行为及可能的金融危机风险。

• 图片参考：

---

4. 估值分析

• 本文聚焦于最优套利PDE的数值求解，不含直接市场资产估值或公司估值。

- 算法通过交易策略找到最小启动资本，经数值概率方法求解。

• 关键输入为市场参数（资产数量n，Bessel过程维度m，时间网格划分，路径数N），波动率稳定模型参数 \(\kappa\)、\(\zeta\)。

- 估值隐含在最优套利策略成本函数 \(u\) 中，反映称为相对“套利价格”。

• 通过时间变换的Bessel过程链接，保证过程的正性和数值稳定。

- 无直接敏感性分析，但网格和路径数的变化会影响数值准确度与计算消耗。

---

5. 风险因素评估

• 数值风险：

- 高维PDE面临的“维数灾难”导致计算成本急剧上升。
- 离散化导致的溢出和精度损失，特别是资本数值接近零时。

• 模型风险：

- 依赖贝塞尔过程和时间变换假设，可能对极端市场条件适用性有限。
- 多解现象可能导致不同求解路径对应不同套利策略，增加实操复杂度。

• 算法风险：

- 插值方法（线性与贝塞尔桥）可能引入误差，影响最终策略准确性。

• 缓解方案：

- 使用贝塞尔过程的时间变换策略防止资本接近零的溢出。
- 采用反射型BSDE框架保证非负解并处理障碍约束。
- 提出基于蒙特卡罗的多样本路径估计提高统计稳定性。

---

6. 批判性视角与细微之处

• 假设限制：

- 市场模型假设n维布朗运动完全独立，未考虑市场相关性的复杂性。
- 利用特定的Bessel过程结构，虽然增强数值稳定但是否适应所有实际市场未知。

• 多解处理：

- 虽有反射BSDE等处理框架，但多解问题本质上尚无统一最优理论，实际应用仍显复杂。

• 数值细节：

- 文章中数据插值的选择与影响提及有限，插值误差和时间步长如何权衡未深入揭示。

• 算法复杂度：

- 虽拓展性讨论了深度学习方法，但现算法仍受限于莫大的计算量，对实际规模较大市场仍有巨大挑战。

• 报告结构一致性：

- 报告逻辑清晰，章节衔接自然，数学推导与数值实验配合紧密。

---

7. 结论性综合

本文围绕波动率稳定市场中的最优相对套利问题，探讨了该问题对应的Cauchy类型偏微分方程的非负最小解的存在性及其数值求解策略。作者通过理论推导揭示该解满足特定的非线性半抛物型PDE，且由于多解及高维的影响，传统网格离散及显式解法难以胜任。

为克服上述困难，作者创新地将资本过程引入时间变换的贝塞尔过程框架中，通过构造合适的随机时钟及利用贝塞尔桥插值方法，构建了适应性强、数值稳定的Monte Carlo模拟算法（Algorithm 3.1），并通过Python实现展示了二维及高维下的数值表现。图1与图2清晰反映了最优套利路径随资本状态和时间变动的规律性，并验证了插值方法对数值稳定性的关键作用。

此外，文中深入探讨了反射型背向随机微分方程（BSDE）方法，将非负最小解问题转化为障碍问题的概率表达，拓宽了PDE求解技术的理论和实践边界，确保了解的非负性和最小性质。该方法兼具理论严谨与实际可操作性，体现了现代随机分析在金融数学中的应用深度。

在风险评估与批判方面，报告虽针对数值溢出、维度灾难及多解性深入讨论，对模型假设的适用边界、插值误差及计算效率亦提出了思考。未来引入深度学习等先进计算技术为多解PDE高维求解提供可能方向。

总之，本文结合数学分析、概率方法和数值模拟，为最优相对套利问题提供了一个稳定、有效、结构清晰的算法框架和理论解析，为波动率稳定市场的套利策略研究及更广泛的高维非线性PDE问题提供了宝贵的参考和技术方法。

---

引用标注

[page::0,1,2,3,4,5,6,7,8,9,10]

报告