• 可变年金合同结构 [page::0][page::3]：

- 结合投资账户价值与保险保障，持有人可在合同期限内随时退保但需支付递减的退保罚金。
- 账户价值动态遵循几何布朗运动，销售费用为账户价值的比例费率。

• 退保定价问题建模 [page::4][page::5][page::6]：

- 采用最优停时理论，将带有时间非齐次且终值不连续的报酬函数的停时问题重构为马尔可夫过程的形式。
- 通过Girsanov变换简化账户价值过程，定义辅助过程Z对合同利益进行参数化，价函数与Z密切关联。

• 非单调最优退保边界及其分析 [page::2][page::8]：

- 证明由于合同结构特殊，最优边界b(t)通常为非单调函数，传统单调边界理论不适用。
- 创新引入单调递增变换β(t) = e^{Λ t}b(t)使边界转化为单调形态，便于连续性及光滑性证明。

• 数值方法与灵敏度分析 [page::9][page::10][page::11][page::12]：

- 采用Picard迭代法求解边界的积分方程，初值选取提高收敛速度。
- 退保罚金率(K)显著影响边界形状与退保时点，K≥费率(c)时无退保激励。
- 死亡率调整对退保边界影响有限，退保罚金为主要驱动。
- 费率(c)和最低保证利率(g)对退保边界显著影响，费率增加退保激励，最低保证利率提升持有激励。

• 合约公平费率与保单价值 [page::11][page::12][page::13]：

| 年龄 | 50 | 60 | 70 |
|------|-----|---------|---------|
| 公平费率(%) | 2.0 | 2.2 | 2.5 |

- 年龄越高，死亡风险越大，公平费用也相应增加以平衡风险。
- 合约价值V₀包含基本欧式价值U₀和退保期权价值V^SO，退保价值随费率提升而增加，随退保罚金增加而减少。

• 理论结果及定理重点 [page::8][page::16][page::17][page::25][page::33]：

- 证实最优退出边界连续（除可能的临界点t*），价函数在边界及状态空间具C¹连续性，二阶空间导数连续。
- 边界满足带奇异核的非线性积分方程，唯一解保证数值计算稳定。

• 量化因子与策略总结：

- 报告构建了一个基于账户价值与退保罚金函数的时变因子b(t)，其单调变换β(t)实现边界的单调性分析，核心是通过变换和界定积分方程设定最优退保策略。
- 无直接量化策略的统计回测，展示最优退保边界随参数敏感性，费率及罚金为关键因子。

• 图示说明：

- 图1显示不同退保罚金强度下退保边界的非单调及“无退保”区间 [page::10]。
- 图2展示退保边界对罚金强度和死亡率参数变动的敏感性 [page::11]。
- 图3揭示费率和最低保证利率对退保边界的显著影响 [page::11]。
- 图4呈现原始边界b(t)及其单调变换β(t)对比，体现理论中变换实用性 [page::25]。

金融研究报告详尽解析报告

——《ON VARIABLE ANNUITIES WITH SURRENDER CHARGES》

---

一、元数据与概览（引言与报告概览）

• 报告标题: ON VARIABLE ANNUITIES WITH SURRENDER CHARGES

- 作者: Tiziano De Angelis, Alessandro Milazzo, Gabriele Stabile

• 发布日期: 未明确指出，文献参考较新，推测为2023年或近期

- 发布机构: 未在文内明示，可能为学术论文或研究报告

• 主题: 可变年金产品（Variable Annuities，简称VA）定价理论，特别聚焦于带赎回费用（Surrender Charges）的早期终止权利的最优行使问题

核心论点与目标：
本论文致力于从严格的数学理论角度出发，建立带赎回费用的可变年金的定价模型，并以最优停止理论刻画政策持有人行使提前赎回权的最优边界。该研究突破了传统依赖单调性假设的最优停止边界分析框架，提出了适应非单调边界的新技术方法，论证边界的连续性与正则性，并提供数值实验支持理论结果。作者意图传达的信息包括：赎回费用结构是影响可变年金价值的核心因素，基于理性完全信息假设的最优行使策略为保险公司风险管理和合约价值评估提供有效依据。报告还提出了求解最优赎回边界的积分方程，有利于实际数值计算。[page::0,1,2]

---

二、逐节深度解读

1. 引言部分：

• 关键论点：

可变年金结合了市场投资表现和保险保障，包含了多种内嵌金融期权，赎回权允许持有人在合约期限内提前终止，但需承担递减的赎回费用，赎回行为影响发行人负债风险，尤其流动性风险，是VA定价和风险管理的重要课题。

• 推理依据：

文献回顾指出赎回风险模拟多样，包括基于强度模型及理性最优行使的两大思路。后者为发行人最不利情形，提供定价上界，已存在部分数值方法但理论分析不足。

• 数据及假设：

定价问题被建模为带时间非齐次支付函数且末端支付不连续的有限期最优停止问题，赎回费用随时间递减，保证金与账户价值相关，账户价值视为几何布朗运动，死亡时间与市场运动独立，死亡率采用确定性函数。

• 模型难点与贡献：

最优边界非单调且非光滑，传统理论不适用，本文提出变换参数、构造单调辅助边界的方法及相应积分方程，既保证理论严谨，也方便数值实现。[page::0,1,2]

2. 模型数学表述（Section 2,3）：

• VA账户模型:

账户价值$Xt$遵循几何布朗运动： $\mathrm{d}Xt = Xt[(r-c)\mathrm{d}t + \sigma \mathrm{d}\tilde{W}t]$，其中$r$为无风险利率，$\sigma$为波动率，$c$为账户价值比例连收费率。

• 死亡时间建模：

死亡时间$\taud$独立于金融市场，死亡概率通过死亡率函数$\mu(t)$的积分给出。

• 支付结构:

- 合约存续至期满时，持有人选择账户价值$XT$与保证滚动本金$x0 e^{gT}$中的较大者。
- 死亡时，同样支付最大值。
- 持有人可提前赎回，获得折扣账户价值$(1-k(t))Xt$，赎回费用$k(t)$递减至期满为零。

• 最优停止问题:

设止付时间$\tau$，VA价格为$V0 = \sup{\tau} \mathbb{E}[\cdots]$，其中赎回支付或持满期支付均纳入计量。

• 测度变换与变量替换:

通过Girsanov测度变换引入等价鞅测度$\mathsf{P}$，定义辅助过程$Zt = x0 e^{g t} / Xt$，使定价问题变为对$Z$的最优停止问题，支付具体形式转化为与$Z$及赎回函数相关的期望。

• 价值函数和停止区域:

定义$u(t,z)$为VA价值函数的变换形式，并用$w(t,z) = u(t,z) - (1-k(t))$简化表示。

• 关键函数与假设:

设定函数$f(t)$与赎回费用及死亡率相关，假设$f$仅单调改变符号，保证最优边界结构合理。

• 定理摘要（Theorem 2.6）：

存在函数$\ell{x0}(t)$表示赎回边界，其形式是账户价值对应于$Z$边界函数$b(t)$的反映，$b(t)$为特定积分方程唯一连续解；赎回最优时机为账户价值首次超过该阈值；VA价格公式包括欧式部分和赎回收益的平滑加权期望。[page::3,4,5,6,7,8]

3. 数值分析与经济含义（Section 3及图形表格解读）

3.1 最优赎回边界数值方案

• 采用Picard迭代离散求解积分方程，确定边界函数$b(t)$的数值解，初始猜测及收敛过程均有说明。

3.2 赎回费用对边界影响（Figure 1）

• $K=1.4\%$时，赎回边界$t^=0$，头几年只有大账户值才赎回，临近期满赎回阈值逐渐下降，曲线非单调；

- $K=2.2\%$时，$t^=1.5$年，初期高赎回费阻止早赎回，赎回区域从$t^*$起呈下降趋势，赎回界限逼近初始账户价值；

• 赎回费$K\geq c$则没早期赎回激励。

3.3 赎回费与死亡率敏感性（Figure 2）

• 赎回边界对赎回费$K$极其敏感，随$K$升高，赎回阈值明显升高；

- 死亡率变动幅度对赎回边界影响较小，阈值变化最大约3%，突显赎回费用对策略决策的主导影响。[page::9,10,11]

3.4 费率与最低保证利率影响（Figure 3）

• 费率$c$增加，持有人赎回激励增强，边界下移；

- 保证利率$g$提高，持有人倾向于持有合约，边界上移；

• 表1显示，老人群体对应较高的“公平费率”，体现人口死亡风险对产品定价的影响。

3.5 风险利率差异敏感性（Table 2）

• 固定其他参数，$r-g$扩大会降低欧式和总合约价值，但赎回期权价值随之升高；

- 赎回选项价值随费率$c$升高增加，赎回费率$K$升高减少赎回选项价值；

• 有利于发行的方案为低费低赎回费场景，且最好保持较低的$r-g$差距。[page::11,12,13]

---

三、图表深度解读

图1（页10） — 最优赎回边界示意图

• 描述: 展示赎回费用两种参数下，赎回边界$\ell{x0}(t)$随时间变化，及对应的赎回区域$\mathcal{D}$与持有区域$\mathcal{C}$。

- 解读: 赎回界面形态因赎回费用显著变化，较小赎回费允许较早赎回，边界非单调，赎回激励显著；大赎回费时期内无赎回，赎回界面严格递减，临近期满赎回激励恢复。

• 文本关联: 直观支撑赎回费用为策略及合约价值主要驱动因素的观点，印证理论假设和数值方法的有效性。

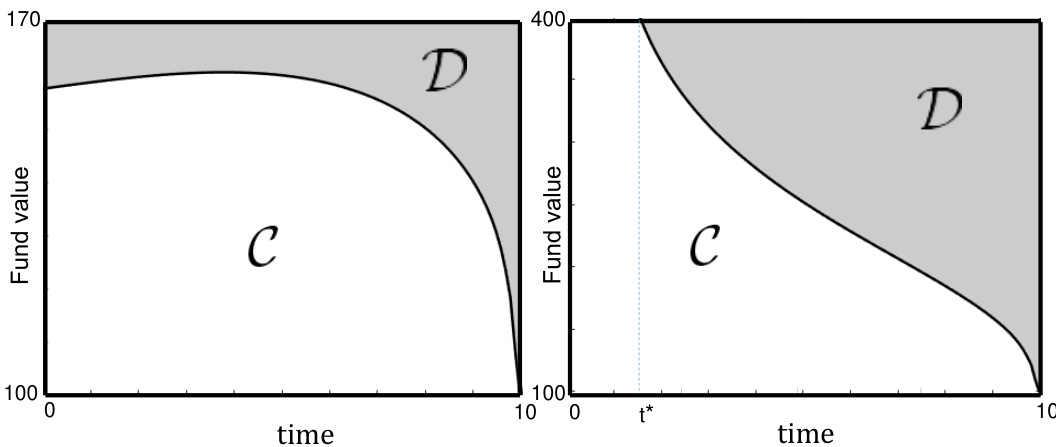
图2（页11） — 敏感性分析（赎回费率vs死亡率）

• 描述: 左图为不同赎回费率$K$下赎回边界变化，右图展示通过乘数调整死亡率$\bar{\mu}$的边界变化。

- 解读: $K$变化引起边界显著上移，死亡率调整对边界影响较小，边界形态稳定。

• 文本关联: 强调赎回费用对持有人行为影响更大，死亡率的影响在本模型、假设条件下相对次要。

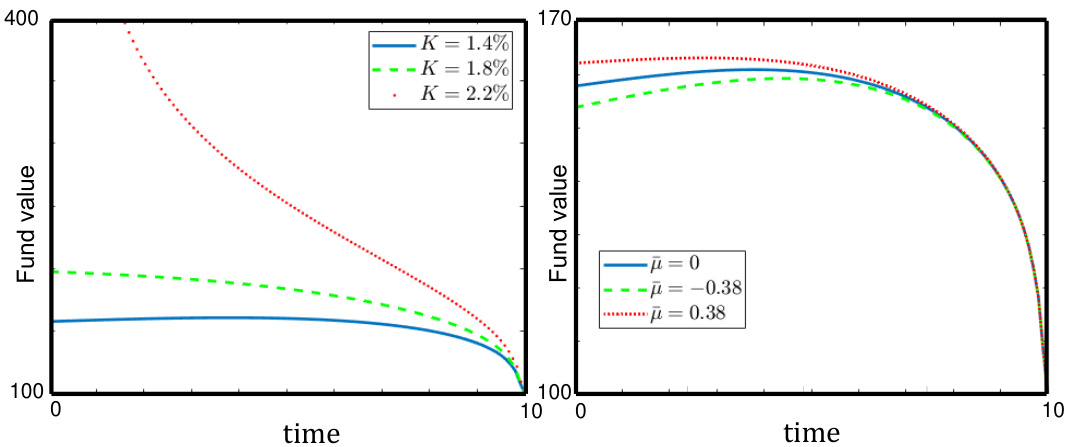
图3（页11） — 敏感性分析（费率$c$与保证利率$g$）

• 描述: 显示费率增高导致持有人更早赎回，保证利率升高促进持有，边界上下移动明显。

- 解读: 费率和保证利率对价值与策略均产生关键影响，定价和产品设计应权衡。

• 文本关联: 体现费率作为保险公司收入组成的重要性及保证利率作为合约吸引力核心因素。[page::11]

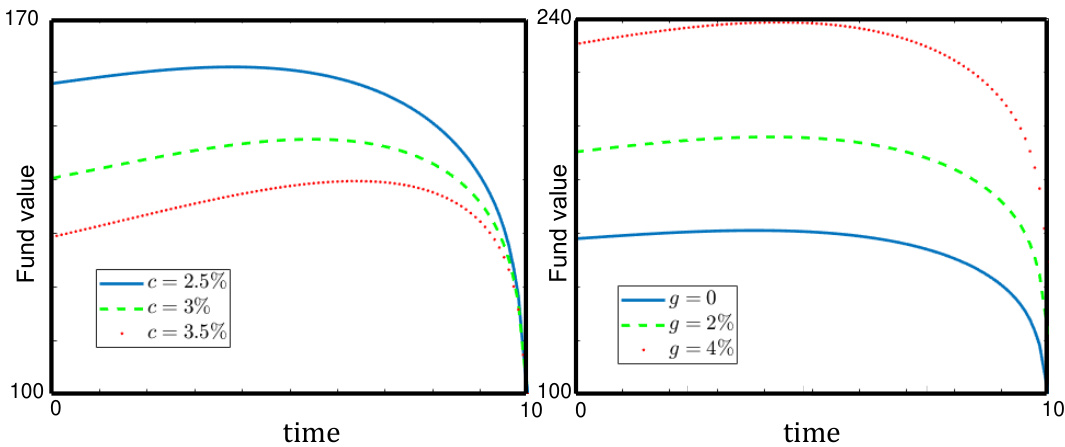
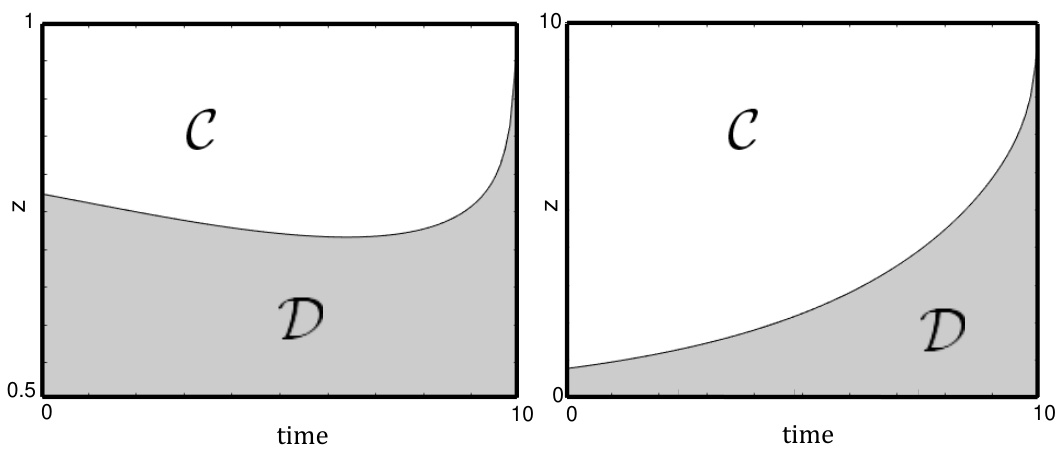
图4（页25） — 最优边界$b$与变换边界$\beta$

• 描述: 左图为原边界$b(t)$，显示其非单调性质；右图为指数变换后的边界$\beta(t)$，显示严格单调性。

- 解读: 变换$\beta$使边界单调化，算法与理论分析更为简便，保证边界连续性和唯一性，技术创新点凸显。

• 文本关联: 赎回边界的单调性转化是理论突破，支撑后续积分方程求解及分析。[page::25]

---

四、估值分析

• 估值方法:

本文通过最优停止理论，将持有者的提前赎回权利视作内含美式期权，构建了基于几何布朗运动账户价值的有限时限最优停止问题。利用鞅测度变换和辅助变量$Z$，通过解析和积分方程精确刻画合约价值及赎回边界。

• 关键输入与假设:

- 市场参数：无风险利率$r$、波动率$\sigma$
- 费率$c$，赎回费用功能$k(t)$，死亡率函数$\mu(t)$
- 账户价值初值$x0$，最低保证利率$g$
- 持有人死亡时间与市场独立，且寿命力$\mu(t)$满足技术假设

• 估值公式总结（定理2.6）:

- 价值$V0$分欧式无提前赎回部分和提前赎回增值部分组成，后者基于最优边界函数表达，并通过积分方程计算。
- 最优赎回边界$\ell{x_0}(t)$与辅助函数$b(t)$有一一对应关系，$b(t)$满足特定非线性积分方程，并且在定义域内唯一且连续。

• 敏感性与公平费率:

通过数值模拟，分析对关键参数如赎回费用强度、费率、保证利率、死亡率的敏感性，推导不同年龄层公平费率区间，辅助产品设计与风险管理。

---

五、风险因素评估

• 已识别风险：

- 赎回风险: 持有人提前赎回行为难以预测，赎回率与赎回费用结构密切相关，过多赎回可能引发发行人流动性压力。
- 市场风险: 账户资产价值受市场波动影响，波动率变化对价格及边界均有影响。
- 死亡风险: 持有人寿命不确定性通过死亡率函数$\mu(t)$体现，对价格影响较赎回费较小。

• 风险缓解策略:

- 设计合理赎回费用递减结构以阻碍初期高频赎回。
- 控制费率水平和保证利率，平衡产品吸引力与风险。
- 精准建模死亡率，根据目标客户群调整费率。

• 模型限制: 假设完全理性持有人、死亡时间不可观测且独立，忽略交易成本及非系统性行为因素，风险偏好未直接计入。

---

六、批判性视角与细微差别

• 模型假设的理想化：

假设持有人完全理性，在市场视角下优化赎回策略，忽略非财务动机和行为偏差，尽管文中提及其他研究含有行为因素。

• 赎回费单调递减且光滑的假设：

实际弃约费用可能更复杂，不完全符合同质单调且二维光滑函数，可能影响赎回行为模式。

• 最优边界非单调性处理创新但复杂：

文中提出的边界变换与积分方程虽然优雅，但数学推导复杂，实际应用时对参数敏感，数值稳定性需关注。

• 死亡率影响较小结论有待实证检验：

在本模型设定下死亡率对价格边界影响较小，但特殊群体或金融危机下可能不同。

---

七、结论性综合

本论文系统性地理论建模并解决了带赎回费用的可变年金的合理定价问题。作者从金融和精算角度创新地将赎回权利嵌入最优停止框架，面对内在的非单调最优边界，提出了独特的边界变换方法，使边界单调化，通过完整的数理分析和非线性积分方程确定赎回边界，保证定价模型的严密性和实际可用性。

关键发现包括：

• 赎回费用结构 是定价和策略决策的主要驱动力，赎回费率与赔付率密切关联，赎回费用过高则完全消除早期赎回动力。

- 死亡率调整对边界影响轻微，风险管理中赎回行为比死亡风险更关键。

• 费率和保证利率变化显著影响策略，体现了保险合约设计的双重目标——保障提供与吸引合理性。

- 积分方程与边界变换 为数值解法带来显著便利和计算效率，助力实践应用。

• 理论贡献 首创性地突破了多数最优停止问题依赖单调性的传统限制，填补了可变年金带赎回费用定价理论的空白。

总之，报告定量精细，理论与数值相辅相成，为保险公司产品设计、风险控制和资产负债管理提供了坚实的数学基础和实务工具，其积分方程和最优边界解法兼具创新性和实用性。

---

以上分析严格基于文本内容及表格/图表数据，引用如下页码：
[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]

报告