研究背景与问题提出 [page::0][page::1]

• 多维随机微分方程模型具有高维参数空间，带来计算复杂度和时间成本的显著增加。

- 采用切片逆回归(SIR)作为监督维度约简方法，有望在保持数据解释能力的同时，提高参数推断效率。

Heston模型及直接推断方法介绍 [page::5][page::6]

• Heston模型由资产价格和方差两个维度随机微分方程组成，具备随机波动率特征。

- 采用欧拉-马鲁雅玛离散化并基于极大似然估计(MLE)构造参数估计的对数似然函数。

切片逆回归与切片推断方法构建 [page::6][page::7][page::8]

• SIR通过对响应变量划分区间（切片），提取最具解释性的特征子空间，显著降低数据维度。

- 在Heston模型框架下，采用MLE对降维后的数据进行参数估计，提出“切片推断”方法。

• 该方法适用于原始数据满足多元正态分布假设，理论上保留了概率结构的可微性。

数值实验设计与参数设定 [page::12][page::13]

• 设定合理的模型参数区间并控制随机性，模拟单路径及多路径资产价格数据进行方法对比。

- 性能指标使用均方误差(MSE)评估拟合路径与真实路径间的距离。

• 约250个时间步长，10个切片，维度降至6。

单路径实验结果分析 [page::14]

• 切片推断(SI)在多数单路径运行中MSE显著优于直接推断(DI)，表现出对路径噪声的更好鲁棒性。

- 直接推断存在MSE极端离群值，表明其对有限数据的敏感性较高。

多路径实验结果及计算效率 [page::15]

| 路径数 (n) | 计算时间 (秒) DI | 平均 MSE DI | 计算时间 (秒) SI | 平均 MSE SI |
|------------|------------------|-------------|------------------|-------------|
| 50 | 47.2 | 0.1420 | 8.1 | 0.4017 |
| 100 | 90.7 | 0.1757 | 15.3 | 0.3885 |
| 250 | 244.5 | 0.2078 | 36.3 | 0.4792 |

• 多路径场景下，DI的拟合效果优于SI，但SI计算时间大幅缩短，特别在样本量大时优势明显。

参数路径拟合与模型敏感性 [page::16][page::17]

• 可视化结果显示SI能较好捕捉资产价格与波动率路径趋势。

- SI方法模型无关，便于扩展且适用于更复杂多维SDE模型。

结论与未来展望 [page::17][page::18]

• SIR作为维度约简方法在多维随机微分方程参数推断中有效，尤其在单路径和有限数据情形下表现稳健。

- SI方法计算效率显著提升，能应对大规模路径数据。

• 未来可探索基于时间动态参数估计以及更复杂模型中的应用和扩展。

金融研究报告详尽分析报告

---

1. 元数据与概览

报告标题：《The Approach of Sliced Inference in Systems of Stochastic Differential Equations with Comments on the Heston Model》
作者：Ahmet Umur Özsoy
所属机构：Gebze Technical University，Department of Industrial Engineering
日期：未明确标注（文献中提及最新引用2024年）
研究主题：

• 利用维度约简技术——Sliced Inverse Regression (SIR)，在多维随机微分方程（SDE）模型中进行参数推断

- 特别针对金融领域中极具代表性的Heston模型展开分析

• 探讨通过SIR降维后再用最大似然估计（MLE）进行参数推断的“切片推断(sliced inference)”方法

核心论点与目标：
报告提出了一种在多维金融随机微分方程参数估计中，通过先进行维度约简（SIR）再进行MLE的“切片推断”，旨在大幅度减少模型高维参数空间的计算复杂度，同时保持合理的估计精度。作者论证该方法可减轻计算资源消耗，尤其在大规模路径仿真与参数估计中表现突出，甚至在某些数据样本量较小的情形下优于直接推断。该报告首次将SIR方法系统性应用于随机微分方程参数估计，具有创新意义。

---

2. 逐节深度解读

2.1 摘要与引言

报告开篇指出，现代金融模型常带有高维度的随机微分方程系统，虽然可用于捕捉复杂关系，但导致参数空间膨胀，计算代价激增。从现实角度考虑，面对数据多、计算资源紧张，迫切需要降维技术以在减缓计算压力的同时保留有效信息。SIR因其监督学习特性及计算简洁性，被选作降维工具。核心前提是即使维度降低，模型通过MLE推断参数仍保持良好性能。作者特别强调SIR可在无须明确模型假设的前提下直接用于参数估计，大大增强其泛用性且适合金融领域的非线性与多变量复杂环境[page::0,1]。

2.2 理论基础与模型背景

• 随机微分方程(SDEs)与Heston模型：

报告承认从Black-Scholes-Merton模型以来，基于SDE的多变复杂模型层出不穷，尤其Heston模型因具有随机波动率的特性而在金融衍生品定价中占据重要地位。其模型包含五个参数（资产漂移$\mu$，方差过程中均值回复率$\kappa$，长期均方差$\theta$，波动率的波动率$\sigma$，以及两个布朗运动间相关系数$\rho$），维度较高且参数估计具挑战性[page::2,5]。

• 直接推断（Direct Inference）：

利用Euler-Maruyama方法离散化Heston模型，形成观测数据的联合概率密度函数。MLE方法在此基础上构建对数似然函数（公式10），并通过数值方法拟合参数。作者强调选择$\frac{S{t+1}}{St}$的简单收益率作为主要建模对象，避免对数收益率带来的复杂性[page::5,6]。

2.3 SIR与切片推断（Sliced Inference）

• SIR方法介绍：

SIR作为一种监督式降维方法，通过对目标变量$Y$的取值范围分割成多个区间(slices)，计算每个slice内标准化预测变量$X$的均值向量，获得协方差矩阵$\hat{V}$的特征分解，选取前几大特征值对应的特征向量组成投影矩阵$W$，实现将高维数据投射到较低维度空间。这一过程强调保持数据对目标变量的预测信息不受损失[page::6,7]。

• 为何使用收益率$Qt$代替价格$St$为目标变量：

$St$分布偏态严重，均等宽度分片可能导致某一区间数据稀缺或无观测点，导致估计偏差和不稳定。$Qt$相对更平稳均衡，适合SIR的分片处理[page::7]。

• X矩阵的构造：

报告设计了一个包含参数$\mu,\kappa,\theta,\sigma,\rho$及方差过程观测数据$vt^i$的6维特征空间作为投影基础。投影后利用MLE对降维数据的正态分布进行参数估计。尽管降维后数据不再是直接的路径数据，但基于多元正态假设，利用$\muX$和$\SigmaX$的线性变换依旧可构造对数似然函数，实现MLE估计[page::8,9]。

• 均值和协方差结构：

其中特别设计$\muX$包含1+漂移$\mu$和长期均值$\theta$两个参数预期值，协方差矩阵$\SigmaX$则近似包含波动率过程的方差和它与收益率的协方差（利用$\rho$和$\sigma^2\theta/2\kappa$拟合）以及对固定参数赋予极小的正数以避免计算稳定性问题[page::10,11]。

2.4 参数估计实践与数值实验设计

• 优化技术选择与参数约束：

因Heston模型的似然函数可能呈现非凸且存在局部极值，作者偏好L-BFGS-B算法，通过对参数空间施加边界（保证Feller条件满足），有效避免估计过程中参数取值失控。选取了现实中较符合市场经验的参数起始点，如年化漂移$\mu=0.03$，均值回归速度$\kappa=5$等[page::11,12]。

• 评价指标设计：

选用均方误差(MSE)综合考察在所有路径及时间截面的误差表现。此指标更适合路径依赖型金融产品估计效果评价[page::12]。

---

3. 图表深度解读与数值分析

3.1 表格1：单路径下DI与SI的MSE表现比较

| 仿真次数 | MSE-直接推断 (DI) | MSE-切片推断 (SI) |
|----------|------------------|------------------|
| 10 | 0.6295 | 0.2484 |
| 15 | 0.7869 | 0.2809 |

• 解读与意义：在单路径样本条件下，切片推断不仅表现出更低的均方误差，且稳定性明显优于直接推断。DI在极端噪声路径情况下产生了极大误差，SI则解决了该问题，表现出更强的鲁棒性[page::13]。

3.2 图1：不同随机种子单路径的MSE比较

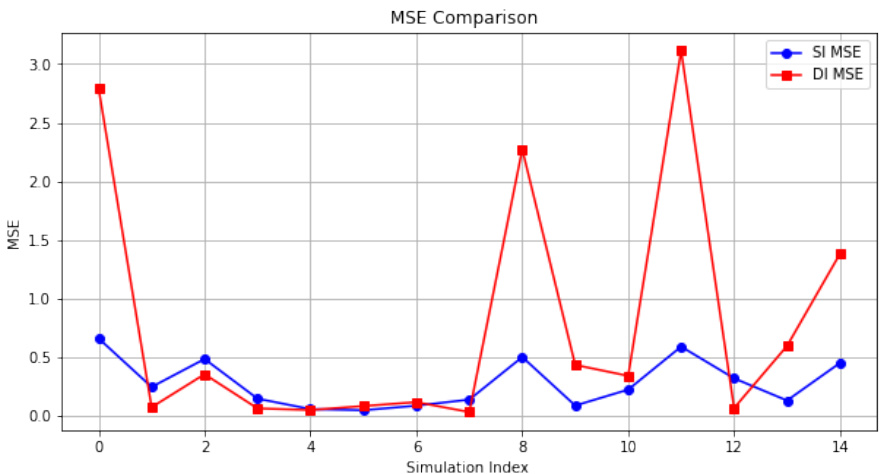
• 数据趋势解读：

图表显示SI曲线稳健，未出现尖锐的MSE突增，DI则存在数个异常峰值。这进一步印证了SI在单路径及小样本场景中的优异表现，减少了估计的极端偏斜风险[page::14]。

3.3 图2：固定随机源，多路径（n=50）MSE比较（含/去极端值）

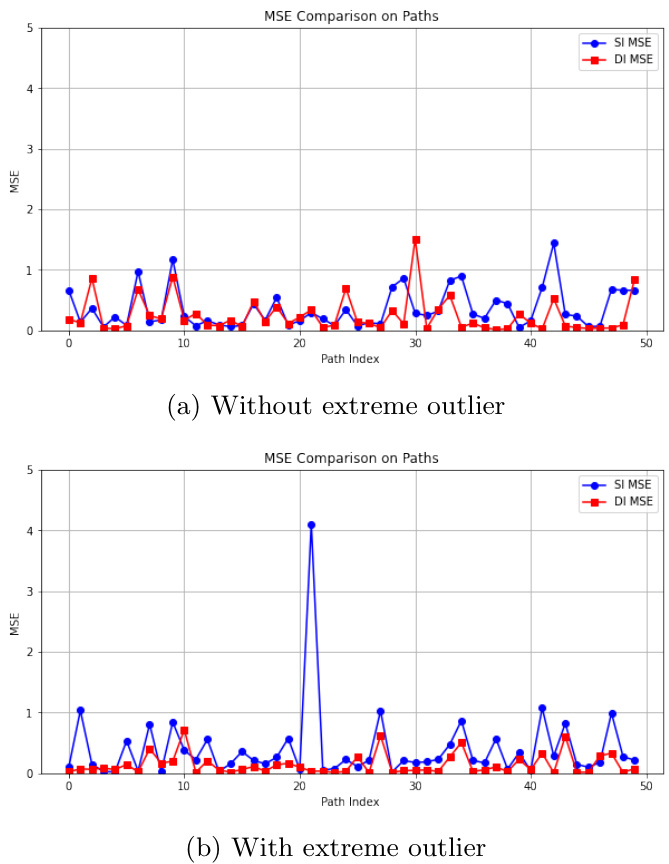
• 趋势解读：

- 去极端值（图2a）：DI与SI表现相近，DI略优。
- 含极端值（图2b）：SI出现极端峰值少，DI极端峰值较多，进一步支持前述单路径稳定性论断。

• 说明随着路径数增加，DI优势逐渐显现，但SI表现依然可接受，仍然可视为良好替代方案[page::14,15]。

3.4 表格2：多路径下计算时间与MSE统计

| 路径数量n | 计算时间（秒） | 平均MSE |
| --------- | -------------- | ---------- |
| 50 | 47.2 (DI) | 0.1420 (DI)|
| | 8.1 (SI) | 0.4017 (SI)|
| 100 | 90.7 (DI) | 0.1757 (DI)|
| | 15.3 (SI) | 0.3885 (SI)|
| 250 | 244.5 (DI) | 0.2078 (DI)|
| | 36.3 (SI) | 0.4792 (SI)|

• 解读：

SI在计算时间上显著优于DI，尤其样本量大幅增长时差异更大（如n=250时，速度提升近7倍），体现出降维方法降低了计算负担的巨大优势。虽然MSE上DI略优，但差距不大，权衡计算效率与精度，SI仍有很大吸引力[page::15]。

3.5 图3：典型路径例子——DI最佳与SI最差拟合结果对比

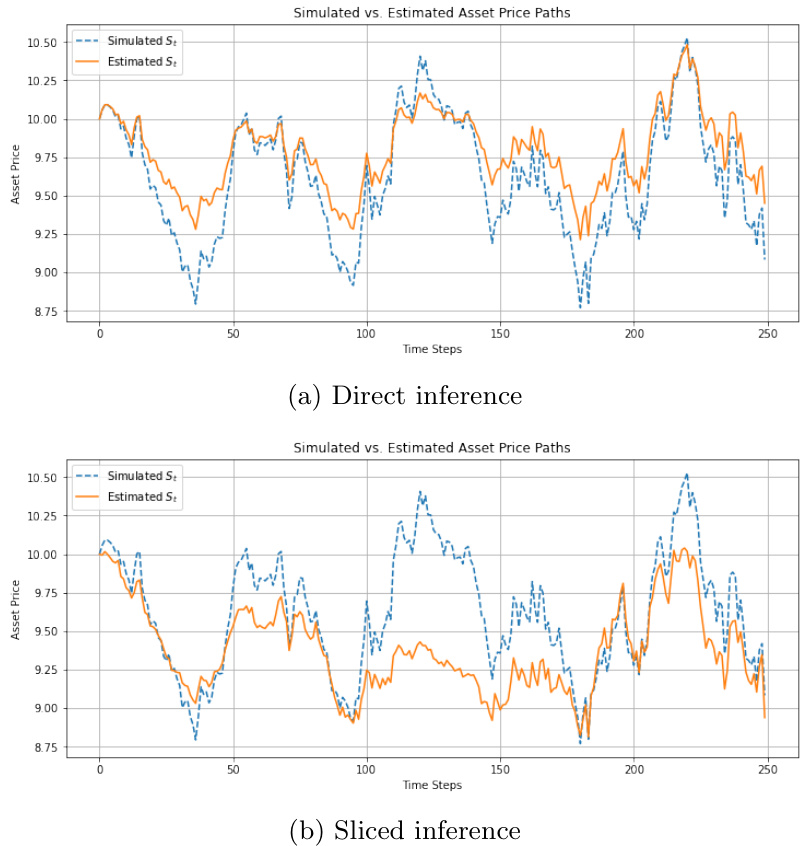
• 趋势解读：

DI最佳路径拟合资产价格与模拟路径吻合度高，细节跟踪紧密。SI最差路径则表现较为粗糙，有明显估计偏离，波动追踪不够精准。但整体趋势与波动水平捕捉仍在合理范畴，表明SI不会严重失真资产价格走势[page::16]。

3.6 图4：波动率路径与自相关函数（ACF）对比

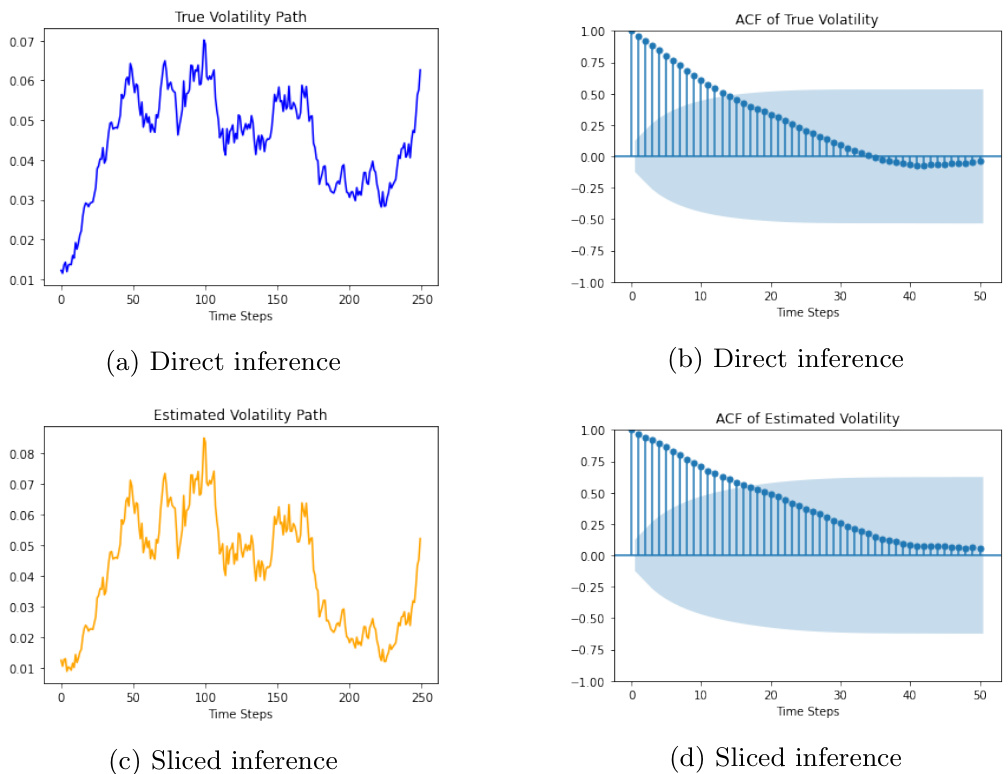
• 解读：

- DI与SI均成功重现了波动率的“簇”特征，ACF衰减趋势与真实路径近似。
- 表明SI尽管降维但仍保留了波动率过程的时间相关性，这是对随机波动率模型结构高度依赖的金融模型成功拟合的关键指标。
- 该表现支持报告结论：SI方法在保持统计特征方面表现良好，能作为实际应用工具[page::17]。

---

4. 估值分析

本报告没有直接涉及估值模型预测（如资产定价、衍生品估价）部分，而是专注于基础的参数估计问题。其估值角度体现在通过最大似然估计(MLE)，在原始高维空间和降维空间分别拟合参数，并对比推断误差及计算效率。

• MLE作为评估似然函数的数值优化过程，其输入对数似然函数依赖于模型假设的正态性及协方差矩阵结构，通过降维得到的线性映射保证了MLE依然可用。

- 报告中对MSE和计算时间的对比即反映了估值的准确性和算法效率权衡。

• 另外通过SIR的线性降维过程间接约束了估值过程的输入空间，提高了在大数据量情况下的稳定性和速度。

---

5. 风险因素评估

作者针对使用SIR在推断中的潜在风险点做了细致阐释：

• 信息损失风险：降维可能导致部分有效数据特征丢失，影响参数估计精度，尤其在数据量较小时风险更大。

- 线性变换假设风险：SIR本质为线性变换，存在对非线性关系拟合不足的可能，尽管实际效果可能适中，但理论上的敏感度未完全厘清。

• 目标变量分片风险：若目标变量分布严重偏态，均分区间会导致部分slice内样本稀少，影响SIR估计稳定性，故选用收益率以提升对称性。

- 算法局限：MLE优化非凸，易陷入局部极值，且SIR变换后的数据可能呈现不光滑问题，导致优化复杂。

• 模型假设风险：协方差矩阵中部分参数假设常数且无波动，忽略参数间潜在相关性，实际应用中需结合专业经验调整。

- 报告强调这些风险未必削弱方法整体有效性，但提醒用户适时评估这些影响并考虑参数约束与初值配置[page::1,3,11,12]。

---

6. 批判性视角与细微差别

• 数据样本限制：报告主要针对合成数据的仿真研究，实证数据中的异常、跳跃以及市场微结构噪声未被充分考量，对实盘数据的适用性仍需验证。

- 降维方法选择：尽管SIR受限于线性加权，非线性关系可能未被充分揭示。报告暗示但未尝试非线性降维方法（如核SIR），在复杂金融模型中或许有改进空间。

• 参数协方差简化设定：协方差矩阵中对非波动参数赋值小常数而忽视其相关性，可能导致估计偏差，特别是涉及时间依赖性的参数，后续研究需补充。

- 未充分讨论算法收敛性与初值敏感度，虽然提及L-BFGS-B的局限，但未给出具体试验数据。

• 模型的推广性：报告强调方法通用，但Heston模型仍是特定类型的二维SDE，推广到更高维或含跳跃的模型还需进一步研究和实验验证。

---

7. 结论性综合

本报告系统地提出并验证了在多维随机微分方程参数推断中引入SIR降维再做MLE的“切片推断”方法，以Heston模型为案例，进行了充分的理论论证和数值仿真验证。

• 理论贡献：首次将监督式维度约简方法SIR融入复杂金融SDE参数估计，设计了一套基于数据变换和线性投影的MLE推断框架。

- 参数估计结果：
- 在单路径数据下，SIR方法表现出更好的稳定性和较低均方误差；
- 在大规模路径数据下，SIR极大缩短计算时间，且估计精度虽有下降，但仍在可接受范围内。

• 图表数据支撑：

- 表1和图1显示单路径下SI优越的MSE分布和鲁棒性；
- 表2和图2展示多路径条件下SI在计算效率方面的明显优势，同时估计精度保持合理；
- 图3、4进一步用路径拟合及波动率自相关妥善印证了SI的有效性。

• 方法优势：

- 简单高效，模型无关，适用于各种多维SDE，无需针对每个模型重构对数似然函数；
- 具备可扩展性，适合包含时间依赖性参数或更高维度参数的扩展研究。

• 实践建议：

- 适合计算资源有限或数据样本稀缺场景，作为参数估计备选或先验降维工具；
- 对参数协方差结构和SIR分片设计须结合域专业知识，确保降维过程中信息损失最小化。

• 未来方向：

- 探索非线性降维方法结合SDE参数推断的潜力；
- 扩展至有跳跃、随机利率等更复杂金融模型中的应用；
- 结合实盘数据与行情，测试模型的泛化与鲁棒性能。

综上，报告严谨、结构清晰，充分论述了使用SIR提高Heston模型参数估计效率和稳定性的创新贡献。该研究为复杂金融模型的实际参数估计提供了一条切实可行的技术路径，兼顾了计算成本和估计质量，具备重要理论价值和应用前景。

---

附录：重要公式与方法梳理

• Heston模型两维SDEs

$$
\begin{cases}
dSt = \mu St dt + \sqrt{vt} St dW{1,t} \\
dvt = \kappa(\theta - vt) dt + \sigma \sqrt{vt} dW{2,t}
\end{cases}
$$

• Euler-Maruyama离散化

$$
\begin{cases}
S{t+1} = St + \mu St dt + \sqrt{vt} St \sqrt{dt} Zs \\
v{t+1} = vt + \kappa (\theta - vt) dt + \sigma \sqrt{vt} \sqrt{dt} Zv
\end{cases}
$$

• 最大似然估计对数似然函数（简化版）

$$
\ell(\theta) = \sum{t=1}^n \ln f(Q{t+1}, v{t+1}|\theta)
$$

参考公式见文中(10), (17)。

• SIR核心投影步骤：

- 标准化$xi$，划分$Y$成若干slice；
- 计算slice均值$\tilde{z}m$，估计协方差$\hat{V}$；
- 特征分解$\hat{V} = \sum \hat{\lambda}i \hat{\eta}i \hat{\eta}i^\top$；
- 选择前$B$个最大特征值特征向量构造降维矩阵$W$，数据降维为$X W$。

• 降维后的参数估计：

$$
X{\text{reduced}} = X{\text{all}} W \sim \mathcal{N}(\muX W, W^\top \Sigma_X W)
$$

对应对数似然函数基于该正态分布进行MLE求解。

---

综上所述，本报告系统介绍并验证了基于SIR的切片推断方法，是金融多维SDE参数估计领域极具启发性和实用价值的贡献。

报告