• 研究框架与方法概述 [page::0][page::1][page::2][page::3]

- 采用拓扑数据分析（TDA），特别是持久同调和持久景观函数，分析时间序列的市场数据，定义并使用L0, L1和C1范数。
- L1范数对应一维洞的持久景观面积，反映市场“混沌度”，值越大，市场越不稳定。
- ζ1范数为修正L1范数，强调市场波动的临界转变。
- L0范数对应零维洞的持久景观第二函数，反映市场分散度和离群点。
- 时间窗口T设为30天，考虑4个单位数据进行对比分析。

• 欧洲股市指数（Ibex35, BFX, ATX, CAC40）案例：L1范数的关键作用 [page::4]

- L1范数准确捕捉2008年金融危机的市场动荡和2020年疫情期间的波动。
- L0范数和C1范数提供补充信息，反映市场结构及动态差异性。

• 南美货币汇率（USD对ARS, CLP, PYG, UYU）案例：L0范数的重要性 [page::5]

- ARS通胀导致其汇率暴涨，造成市场极端不稳定，但L1范数接近零，无法反映市场散布异常。
- L0范数显著上升，有效展示市场因极端指数变化产生的"散布"和分裂现象，表明L0范数对捕捉离群点及市场分散极为关键。

• 加密货币市场（BTC, DOGE, XRP, ETH）案例：ζ1范数用以识别临界波动性 [page::6]

- L0与L1范数较低，暗示市场整体走势类似且稳健，但ζ1范数高企，显示高度波动和临界转变。
- 证明ζ1范数能捕捉到整体同步波动中隐藏的高风险状态。

• 西班牙银行股（La Caixa, BBVA, Santander, Sabadell）案例：三种范数共同验证市场稳定与波动性低 [page::7]

- L0和L1均较低，说明银行股市场增幅及波动接近，波动同质性强。
- ζ1范数低，体现临界转变风险下降，整体市场稳定性良好。

• 综合结论 [page::8]

- L1范数适合揭示总体市场波动和混沌。
- L0范数补充揭示市场离群状态和分散程度。
- ζ1范数有效提示临界转变和风险集中。
- 建议金融时间序列研究结合三者综合使用，以获得更全面市场动态洞察。

资深金融研究报告详尽分析

——《L0范数介绍及L1、C1范数在加密货币、南美货币、银行指数和欧洲股指时间序列研究中的应用》
作者：Víctor Ujaldón García
发布时间：2024年1月12日

---

一、元数据与报告概览

• 标题：《L0范数介绍及L1、C1范数在加密货币、南美货币、银行指数和欧洲股指时间序列研究中的应用》

- 作者：Víctor Ujaldón García

• 发布时间：2024年1月12日

- 研究主题：应用拓扑数据分析（Topological Data Analysis, TDA）工具，尤其是针对时间序列数据中拓扑特征的度量，探索四个不同市场（加密货币、南美货币、西班牙银行指数和欧洲指数）的市场稳定性及临界转变。

• 核心论点：引入新定义的$L0$范数，结合已有的$\zeta1$范数和$L1$范数，利用拓扑数据分析识别市场时间序列中的重要结构，探讨其在不同市场的实际应用，强调多范数互补带来的分析优势和不足。

- 作者意图：说明传统$L1$范数在市场稳定性分析中的局限，引入$L0$和$\zeta1$范数作为补充指标，实现对市场结构、波动和临界状态的更全面洞察。[page::0]

---

二、逐节深度解读

2.1 摘要与引言

• 摘要要点：针对四类金融市场数据应用TDA工具。引入$L0$范数作为本文创新，结合$\zeta1$范数，分析并展示TDA工具在预测市场变化与识别优势和薄弱环节方面的能力。

- 引言解析：市场稳定性研究核心在于捕捉市场行为的突变。传统统计方法计算繁复，受限于参数分布假设。TDA以其无需依赖底层分布的优势，通过持久同调捕获数据的“孔洞”等拓扑特征，快速揭示市场中全局的、组群的运动模式。TDA虽不精确预测未来价格点位，但能有效识别市场整体趋势和转折点。$L0,L1,C1$范数在功能上类似统计学中的$R^2$指标（解释变量的变异贡献程度）。[page::0]

2.2 TDA基础介绍（第2节）

• 核心概念：点云数据$X$通过Vietoris-Rips复形$C\epsilon(X)$的建立，构造不同尺度下的链复形结构。借助边界算子$\partial$，定义链的边界映射，寻找“孔洞”（homology）即闭合回路，使其边界为零。

- 持久同调定义：随着$\epsilon$扩张，记录$n$维孔洞的诞生（birth）和消亡（death），形成持久矩阵$\mathfrak{D}n$。将存活时间映射为山峰形状的函数$f{b,d}(x)$，组合成拓扑持久景观函数$\lambda^k(x)$。

• 范数定义：对这些景观函数计算$L^p$范数（常见为$L1$范数），作为量化拓扑特征的度量。进而定义时间窗内的$Lp$范数，及$Cp$范数（差分法，突出趋势变化）。$Cp$范数详见文献[1]。

- 此部分建立整个报告分析的数学基石，解释了如何将复杂点云数据的拓扑结构转化为可量化的指标。 [page::1]

2.3 方法论细节（第3节）

• $L1$范数重点：专注于一维孔洞持久景观（环状结构）$||\lambda^1(x)||1$，因高维结构计算耗时且信息有限。

- $L0$范数创新：定义为零维持久景观$||\lambda^2(x)||1$（0维孔洞对应连通分量），反映“市场分散程度”。

• 指标含义总结：

- $L1$越大，表示市场越不稳定（环形拓扑更多，表现为价格波动更剧烈）
- $\zeta1$是修正版的$L1$，聚焦临界转变阶段
- $L0$值越大，市场价格差异越大，呈现分散状态

• 时间序列构造：以对数收益率$\log(x{i+1}/xi)$为基本单位，选取时间窗$T=30$，每个时间点对应4个市场单位指数构成点云。

- 该章节清晰定义了所用指标的具体数学形式和市场经济学意涵，为后续市场具体分析提供了工具。 [page::2][page::3]

2.4 数据应用与结果（第4节）

2.4.1 欧洲股指 —— $L1$范数作用

• 分析Ibex35等欧洲四大股指，发现$L1$范数在2008年全球金融危机期间表现出巨大峰值，敏锐捕捉市场极端波动和不稳定。2020年疫情期间峰值较小，因疫情对全球市场影响均匀。

- 结论：$L1$敏感于市场内指数间的“混乱度”和差异性，适合捕捉系统性危机中的波动异常。

• 图1详解：四个图分别为$C1$范数曲线、归一化相对值、$L0/L1$范数对比及绝对归一化趋势走势。峰值及其对应事件的时点清晰揭示$L1$指标的解读逻辑。

- 图像地址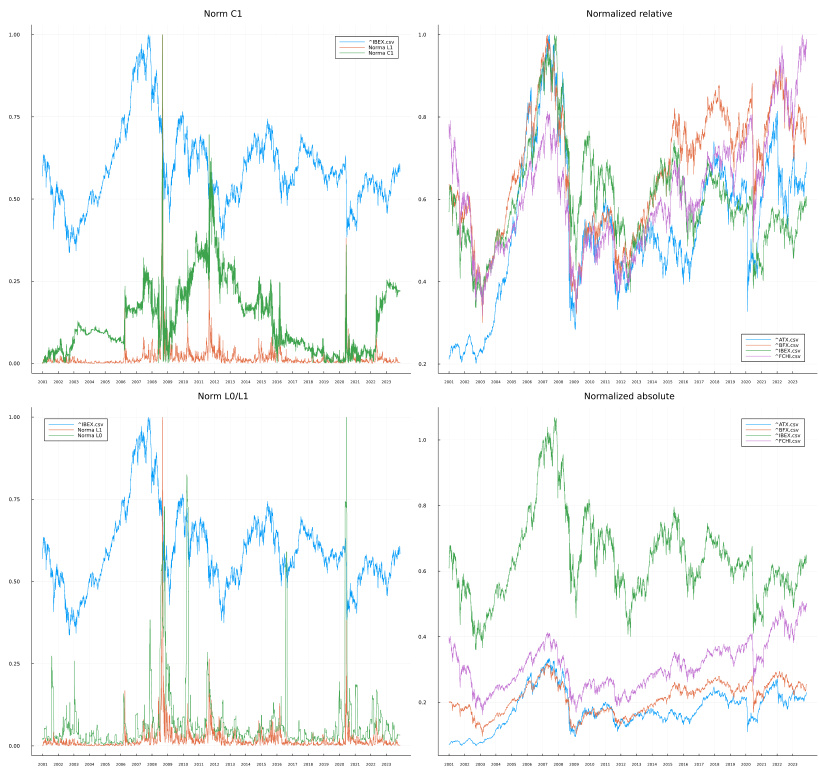： [page::4]

2.4.2 南美货币 —— $L0$范数关键

• 针对美元兑阿根廷比索（ARS）、智利比索（CLP）等，特别提到ARS因通胀大幅贬值，导致市场极不稳定。

- $L1$范数因极端一只货币的飞涨未反映波动（Ripps复杂度被抑制），而$L0$范数迅速攀升，捕捉到价格点云“扩散”现象。

• 这一案例强调$L0$范数在识别部分资产剧烈异动（局部非稳定）时的补充作用。

- 图2呈现四幅图与图1类似的结构，明显展示不同范数的分别与共鸣。

• 图像地址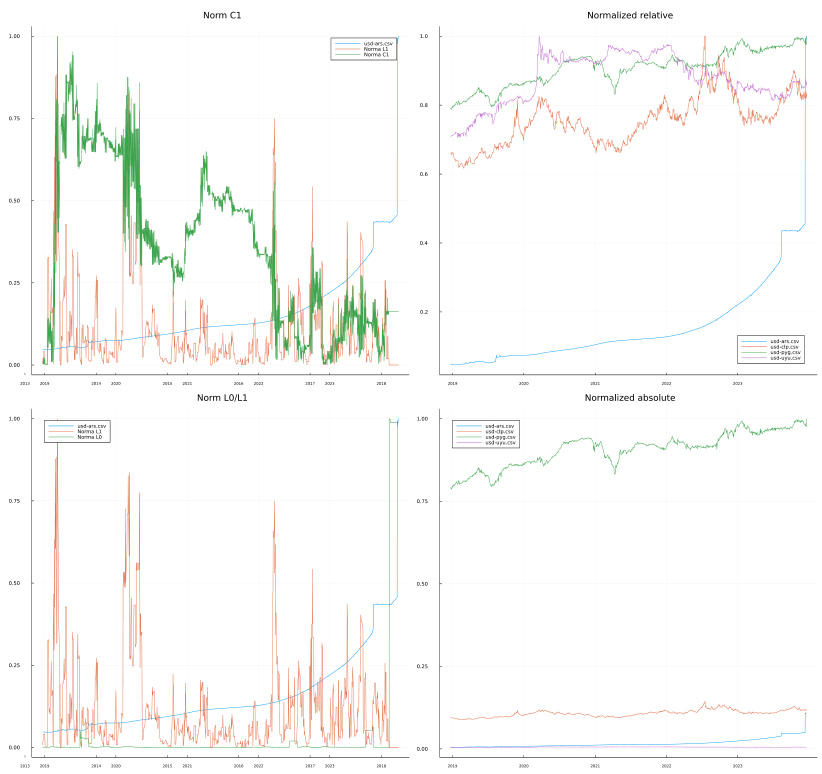： [page::5]

2.4.3 加密货币 —— $\zeta1$范数判断关键临界态

• 针对BTC、DOGE、XRP、ETH对美元汇率做分析。

- 尽管$L0$和$L1$均较低（指示整体同步性较好、市场无大规模分散），$\zeta1$持续居高，反映市场波动性质非常“剧烈”，是一种内生的混乱和临界临近态。

• 说明$\zeta1$范数能补足$L1$对于一致性波动“盲区”的缺陷，捕获更细腻的波动剧烈性。

- 图3四个面板分别展示各范数及归一化值，量化“内在混乱”的不同维度。

• 图像地址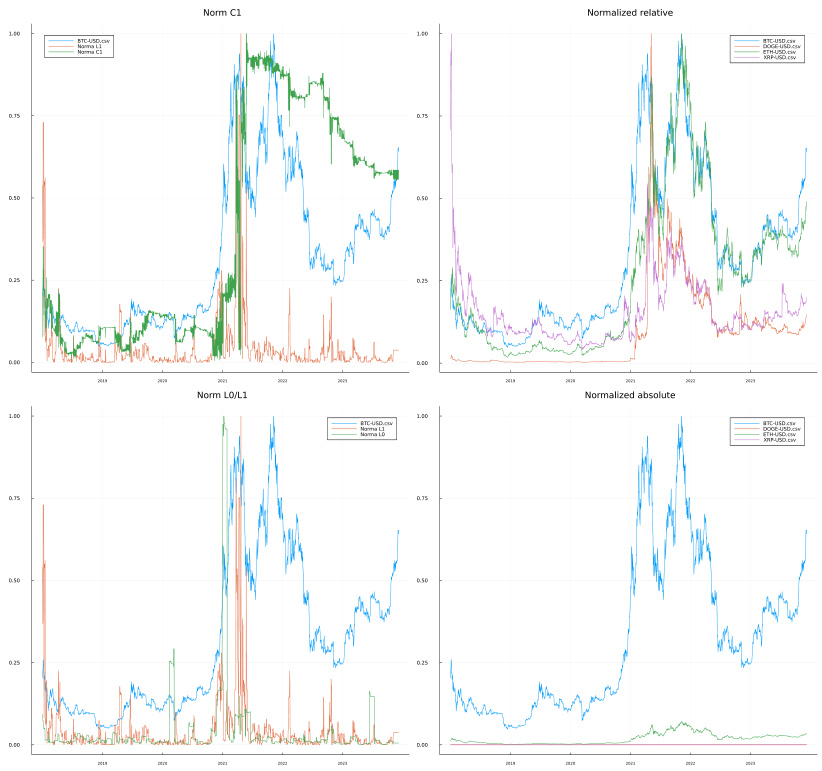： [page::6]

2.4.4 西班牙银行股 —— 多范数联合验证稳定性

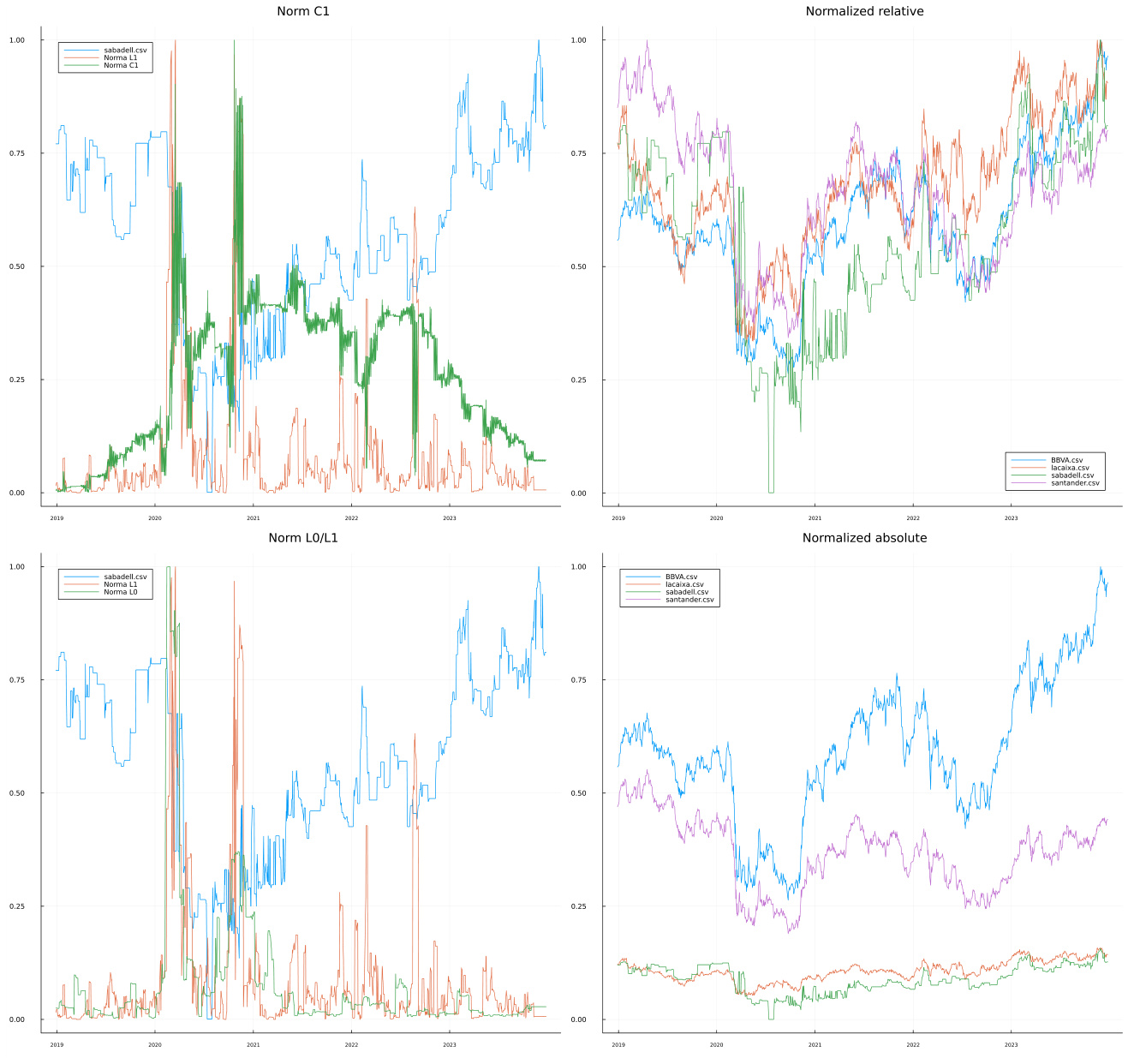
• 调查La Caixa、BBVA、Santander、Sabadell。

- 从归一化相对值看，银行股价走势高度一致，除2020-21年Sabadell短暂崩盘。

• $L0$范数低、$L1$范数低，体现市场统一波动性近似；$\zeta1$数值减少，表明临界波动趋缓。

- 综上，三范数结合验证市场整体稳定且相互联动紧密。

• 图4展示完整指标图，内容和第10页图5重复。

- 图像地址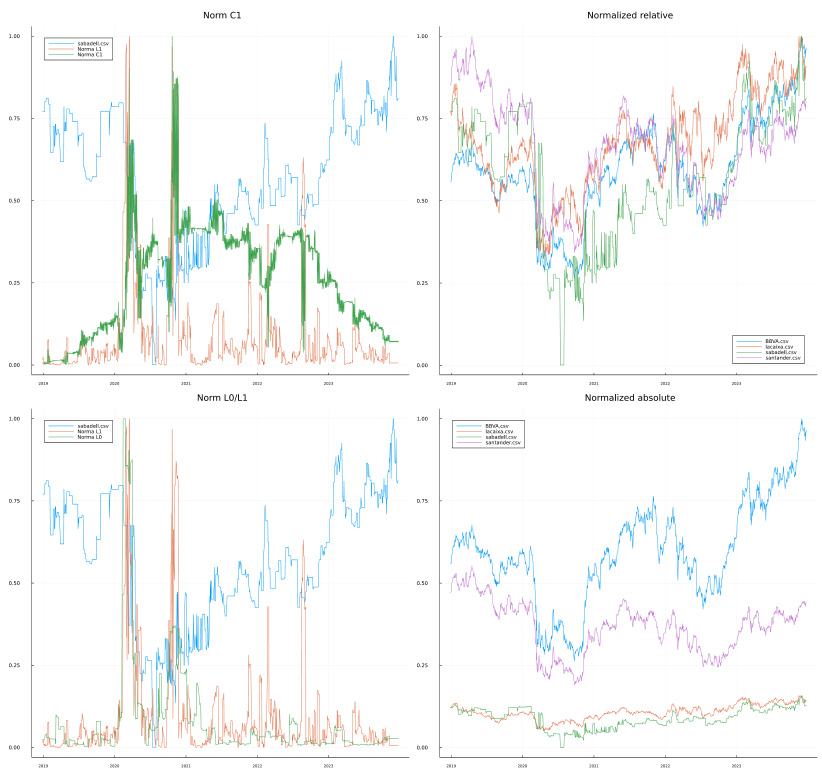：, [page::7, page::10]

---

三、图表深度解读

所有图表均由四个子图组成：

1. Norm C1：展示曲线型的$C1$范数（$C_p$的特例），通过差分捕捉短期拓扑变化动向。

2. Normalized relative：各市场指数分别归一化后时间序列，直观反映价格走势的相对同步性或错位。

1. Norm L0/L1：$L0$和$L1$范数对比，体现市场扩散、混沌和波动强度的相对大小及转换。

4. Normalized absolute：指数绝对值归一化，显示市场规模及其变化趋势。

图表共同支持作者核心观点：

• $L1$擅长捕获多指标间的混乱和不稳定峰值，尤其在系统性事件中作用明显（如欧洲股指2008年危机）。

- $L0$更敏感于指标间分散差异，高度反映局部市场“离群”现象（南美货币极端货币贬值）。

• $\zeta1$则补充$L1$忽视的波动内在剧烈跳跃，反映整体临界转变态（加密货币市场）。

- 三者结合给出更完整的市场状态画像与趋势信息[page::4, 5, 6, 7, 10, 11, 12, 13]。

---

四、估值分析

• 报告主要围绕拓扑指数的计算与解释，未涉及传统财务估值如折现现金流（DCF）或市盈率倍数法。

- 其“估值”核心即是各范数值的计算模型与市场状态的映射：
- $L1$范数基于一维持久景观面积，反映循环类波动性。
- $L0$范数基于零维持久景观面积，反映连通性及市场分散度。
- $C1$范数基于$L1$的时差修正，捕捉市场波动的梯度趋势。

• 文献[1][2]提供相关TDA理论背景和定量方法支持，但报告主体没有敏感度或区间估值分析。 [page::1, 2, 8]

---

五、风险因素评估

• 报告未显式列举传统金融风险因素，例如市场风险、信用风险等。

- 风险隐含于时间序列拓扑结构的复杂变化与不稳定指标的跃变，体现在范数的异常升高或剧烈波动中。

• 作者提醒单一范数风险：$L1$不对局部离群或同步高波动敏感，应辅以$L0$和$\zeta1$指标避免风险被忽略。

- 未见明确的措施或缓解策略，更多是以多元指标交叉验证减少盲点。 [page::5, 6, 8]

---

六、批判性视角与细微差别

• 报告基于拓扑方法，是应用数学在金融分析中的创新体现，但对实际投资决策的直接指导性及精准预测能力有限。

- $L1$范数虽广泛使用，但报告自己强调其缺陷，表明单靠$L1$无法揭示市场全貌，故提出$L0$与$\zeta1$作为补强，体现作者对方法局限性的清醒认识。

• 研究依赖计算量大且涉及多重参数选择（如时间窗口$T$，指标选择$n=4$），但对参数敏感度缺乏系统评估，未来研究有待加强。

- 报告主要描述性，缺乏对范数数值变化背后经济机制的深入剖析，比如为何加密货币的内生波动如此剧烈未作多因子解释。

• 各市场样本和时间段选择差异，可能导致指标对比的可比性受限，报告未详述样本完整性或数据质量检验细节。 [page::2, 8]

---

七、结论性综合

本文通过创新地引入$L0$范数，并结合已有的$L1$及$\zeta1$范数，用拓扑数据分析技术有效挖掘金融市场时间序列数据的内在结构和行为特征。

• 四个市场案例各体现不同范数的优势和针对性：

- 欧洲股指强调$L1$对系统性风险的敏感度（尤其2008年金融危机）。
- 南美货币激烈贬值案例中，$L0$凸显市场离散化，传统$L1$难以捕捉。
- 加密货币市场中，$\zeta1$捕捉高波动临界状态，而$L0,L1$保持稳定。
- 西班牙银行指数展现三类范数联合使用时的稳定和一致性确认能力。

• 图表亮点：4×4子图布局全面展示范数指标和归一化价格序列的交互验证，让读者直观感知拓扑指标与市场实际动态之间的联系。详尽的图注和数据覆盖时间点覆盖10年以上，具备较强的应用探索意义。
• 总评价：作者强调未来时间序列分析应同时考虑$L1$, $L0$和$\zeta1$范数，这不仅丰富了拓扑金融分析工具箱，也为市场稳定性及临界转变状态的早期发现提供了新视角。报告从理论定义到实证应用均体现出较好的系统性和创新性，适合拓扑数据分析及金融市场数学建模领域的研究者借鉴和深化。

综上所述，该报告为金融时间序列中的拓扑结构分析开辟了新路径，将传统统计学难以捕捉的复杂市场行为纳入研究视野，推动TDA方法与金融经济学的融合发展。[page::8]

---

（全文所引用页码均按报告页码标注）

报告