卡尔曼滤波理论介绍与应用框架 [page::2][page::3][page::4][page::5]

• 卡尔曼滤波通过观测数据动态估计系统隐含状态，兼顾先验预测和新观测的加权，优化状态估计。

- 介绍了标准卡尔曼滤波及状态约束卡尔曼滤波，支持等式和不等式的状态变量约束条件，增强模型灵活性。

传统基金行业仓位测算方法回顾 [page::7][page::8]

• 采用Lasso回归避免多重共线性，设定系数非负且仓位总和约束。

- 采用主成分分析(PCA)提取正交主成分后回归，解决变量相关性问题，组合两者改进主题型与非主题型基金的测算。

• 主题型基金采用Lasso回归；非主题型基金采用PCA回归。

基于卡尔曼滤波的基金行业仓位测算模型及约束方法 [page::9][page::10]

• 将基金收益率作为观测值，行业仓位权重视为隐含状态，建立状态空间模型，权重服从随机游走。

- 引入两种约束处理：（1）滤波后加约束：负权重置零后归一化；（2）滤波中加约束：状态约束卡尔曼滤波，算法内嵌权重非负且归一约束。

基金仓位测算实证分析与效果比较 [page::11][page::12][page::13]

• 样本为2014年6月至2021年6月的公募普通股票型及偏股混合基金，入选基金数随时间稳定上升。

不同方法估计误差对比

| 测算方法 | 基金行业仓位误差均值 | 行业平均仓位误差均值 |
|------------|---------------------|---------------------|
| 后约束KF | 2.82% | 0.99% |
| 中约束KF | 3.19% | 1.47% |
| Lasso | 3.45% | 1.45% |
| PCA | 3.48% | 1.78% |
| Lasso+PCA | 3.21% | 1.42% |

• 后约束KF方法显著提升测算精度，行业平均仓位误差比传统方法降低30%以上。

2020年12月31日前十大重仓行业仓位测算对比

• 后约束KF测算结果与实际较为贴合，明显优于Lasso+PCA方法。

行业内不同仓位级别估计误差趋势及前三大行业误差对比

| 排名 | 后约束KF | 中约束KF | Lasso | PCA | Lasso+PCA |
|------|----------|----------|-------|-------|-----------|
| 1 | 2.24% | 5.86% | 3.85% | 6.93% | 4.11% |
| 2 | 1.98% | 2.93% | 3.44% | 5.15% | 3.89% |
| 3 | 1.74% | 3.37% | 2.78% | 3.44% | 2.46% |

• 卡尔曼滤波尤其在前三大重仓行业误差降低40%-50%，显著优于传统方法。

卡尔曼滤波辅助宏观经济数据实时预测与信息冲击分解 [page::14][page::15][page::16]

• 引入动态因子模型（DFM），利用卡尔曼滤波估计宏观经济隐藏因子，处理数据缺失与异频问题。

- 以纽约联储Nowcast模型为例，动态调整美国GDP季度环比增长预测值。

• 实现新数据对目标经济指标预测的边际冲击分解，指导宏观决策。

总结与展望 [page::16][page::17]

• 本文首次尝试将卡尔曼滤波引入基金行业仓位高频测算及宏观经济预测，显著提升了预测准确度和数据更新效率。

- 估计误差相较传统方法大幅降低，具有较强的实际应用价值。

• 卡尔曼滤波潜在应用于基金久期测算及基金经理风格识别，未来值得进一步探索。

报告详尽分析报告

---

1. 元数据与概览

• 报告标题：《如何提升机构仓位测算和宏观数据预测精准度》

- 作者： 郑兆磊、宫民

• 发布机构： 兴业证券经济与金融研究院

- 发布日期： 2022年1月11日

• 主题： 本报告聚焦于利用卡尔曼滤波（Kalman Filter）技术改进机构投资基金仓位的测算精准度和宏观经济数据的建模与预测，进而提升投资研究和宏观经济数据应用的效果。

核心论点： 报告认为卡尔曼滤波作为一种基于状态空间模型和贝叶斯思想的动态估计算法，能够显著超越传统基于线性回归的基金仓位测算方法，减少传统估计的偏误，尤其在重仓行业的仓位估计误差上能降低约50%；同时，卡尔曼滤波结合动态因子模型（DFM）应用于宏观经济数据处理，可实现高维异步数据的实时状态估计和缺失值处理，实时反映宏观经济最新信息及其对GDP等关键指标的冲击。报告还指出卡尔曼滤波在基金久期测算与基金经理风格识别中也具备潜力，预示后续扩展研究。

---

2. 逐节深度解读

2.1 卡尔曼滤波简介

• 章节总结： 介绍卡尔曼滤波的来源、基本定义及其数学形式。卡尔曼滤波是一种通过线性状态方程描述隐含状态变量（$xk$）与观测变量（$zk$）关系的递归优化算法，旨在在噪声和误差影响下获得隐含状态的最优估计。历史上，它主要被用于制导、视觉与信号处理领域，本报告创新提出其在投资领域，特别是基金仓位和宏观数据研究中的应用价值。
• 数学原理详解：

- 状态空间模型中，观测方程 $zk = H xk + \etak$，其中测量噪声$\etak$为均值为0、方差$R$的白噪声。
- 状态转移方程 $xk = A x{k-1} + ek$，其中状态噪声$ek$为均值0、方差$Q$的白噪声。
- 卡尔曼滤波需要结合过去的预测 $x{k|k-1}$ 和当前观测 $zk$，计算后验估计 $x{k|k}$，更新协方差矩阵，关键在于计算卡尔曼增益 $Kk$，平衡历史预测和新数据的权重。(详见公式3~7)

• 关键逻辑： 该方法基于贝叶斯更新思想，通过递归过程减少误差，是最优线性估计，无需历史全部数据即可进行实时估计。
• 技术细节亮点： 状态先验分布预测、状态和观测联合分布构造、后验分布更新求解步骤清晰，推导严谨，且说明可处理缺失数据和动态变化的特性。
• 状态约束卡尔曼滤波简介： 在状态变量存在外生等式或不等式约束的情况下，引入投影优化求解，保证状态估计满足实际约束，如组合权重非负和求和为一等约束条件，（涉及等式约束的闭式求解与不等式约束的数值解转化，详见公式及推导）[page::2-6]

---

2.2 传统基金行业仓位测算方法回顾

• 章节总结： 介绍基金仓位传统测算一般采用线性回归方法，例如Lasso回归和PCA回归，具体做法是将基金单位净值日增长率作为因变量，28个申万一级行业指数加上债券指数作为解释变量，通过带约束的多元线性回归估计行业权重，基于历史数据求取平均仓位。
• Lasso回归：

- 引入$L1$范数惩罚解决多重共线性问题，同时通过正则化实现部分行业仓位零权重，符合实际部分行业持仓为零的情况。
- 约束包括仓位上下限及总股票仓位范围，贴合基金类型差异（偏股混合、普通股票型），例如股票仓位区间为60%-95%不等。

• PCA回归：

- 通过提取主成分降低解释变量维度，解决共线性问题。
- 使用9个主成分覆盖95%变异量，再将主成分回归系数还原为原变量系数估计行业权重。

• Lasso+PCA混合方法：

- 针对主题型基金（行业集中度高）选用Lasso回归，非主题型基金选用PCA回归，以对应基金风格差异，提升准确性。[page::7-9]

---

2.3 基于卡尔曼滤波的基金仓位测算方法

• 核心思路： 将基金行业仓位视为时变的隐含状态$wk$，基金收益率视为测量值$Rk$，利用状态空间模型描述组合权重的随机游走过程与收益率的线性组合关系，即

$$
\begin{cases}
Rk = rk wk + \etak \\
wk = w{k-1} + ek
\end{cases}
$$
其中$r_k$为备选指数当期收益向量（时变矩阵，区别传统恒定测量矩阵$H$）。这样，卡尔曼滤波能动态跟踪并估计基金仓位。

• 初值利用半年报持仓信息，加快收敛： 取基金最近一期半年报持仓作为初值，结合协方差矩阵参数(Q,R)进行迭代滤波。
• 约束处理： 调整滤波结果使其满足非负和权重和为1的约束。两种方法：

- 后约束KF： 滤波无约束，结果后处理去负并归一化。
- 中约束KF： 在滤波迭代中嵌入约束优化，通过投影优化保证输出的权重满足约束。

• 实证研究样本： 2014年至2021年6月，普通股票型和偏股混合型基金，采用申万一级行业指数及债券与货币指数作为非股票资产代理，季度末筛选样本，规模>5000万，排除不完全投向A股基金。
• 结果对比与优劣： 卡尔曼滤波法尤其是后约束KF，在单只基金行业仓位误差上实现2.82%（低于传统Lasso+PCA的3.21%），行业平均仓位误差减少30%以上（0.99%对比1.42%），效果十分显著。

同时，中约束KF表现不及后约束KF，可能因迭代中约束干扰了最优估计过程，降低了估计精度。[page::9-12]

---

2.4 图表深度解读——基金仓位测算部分

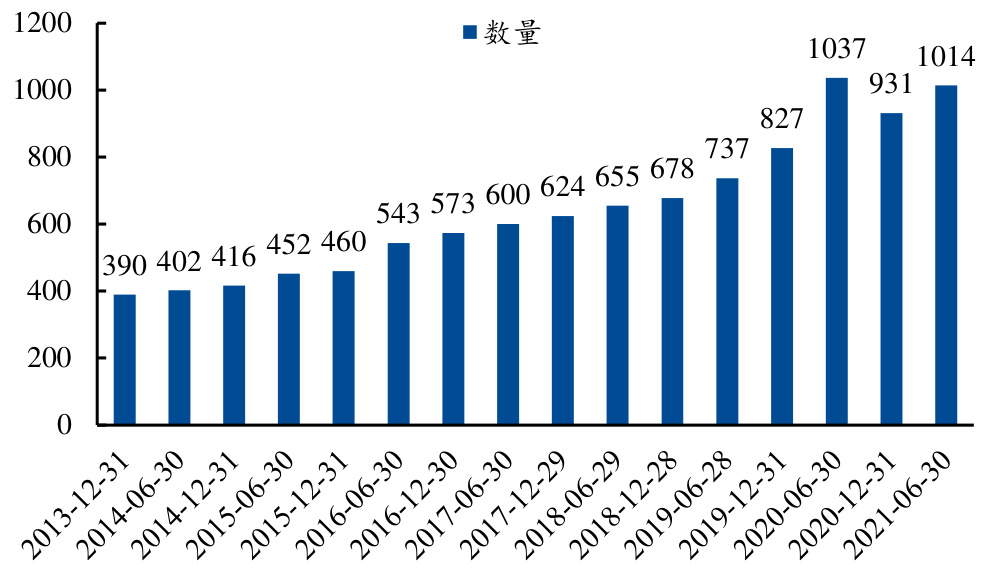
• 图表2：入选基金数量（2013-2021）

描述了样本时期内入选的基金数逐年递增趋势，从约390只增至超过1000只，显示数据样本充分且连续，具有代表性和时效性。

• 图表3、4：基金行业仓位误差均值与行业平均仓位误差均值对比

显示五种测算方法的误差比较，后约束KF方法误差最小，表明卡尔曼滤波在准确度提升上的稳定优势。
- 单只基金行业仓位误差：后约束KF 2.82%，优于Lasso+PCA 3.21%
- 行业平均仓位误差：后约束KF 0.99%，优于Lasso+PCA 1.42%

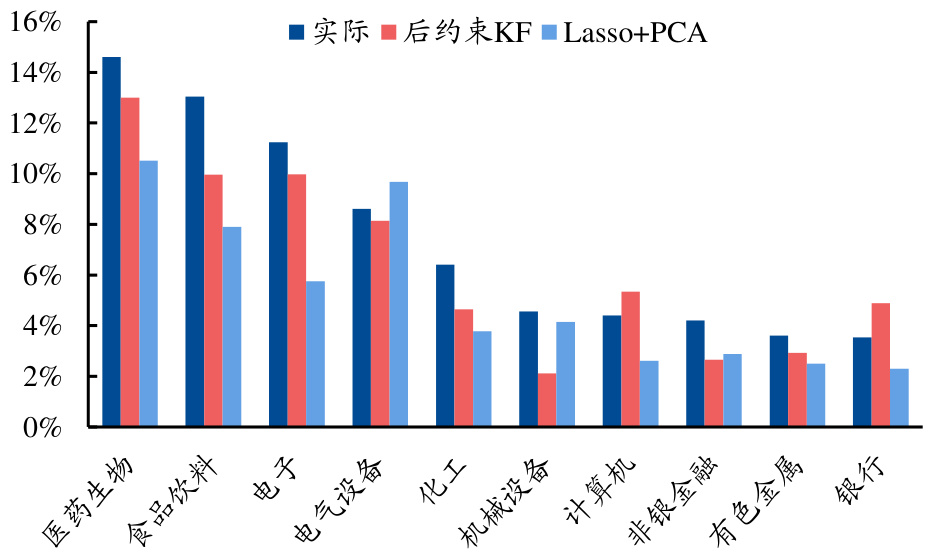
• 图表5：2020年12月底十大行业平均仓位对比

后约束KF的估计结果（红条）与实际持仓（蓝条）高度吻合，Lasso+PCA（浅蓝条）则存在明显偏差，特别在食品饮料和电子行业上误差较大，体现卡尔曼滤波对行业仓位变动的高敏感度和跟踪能力。

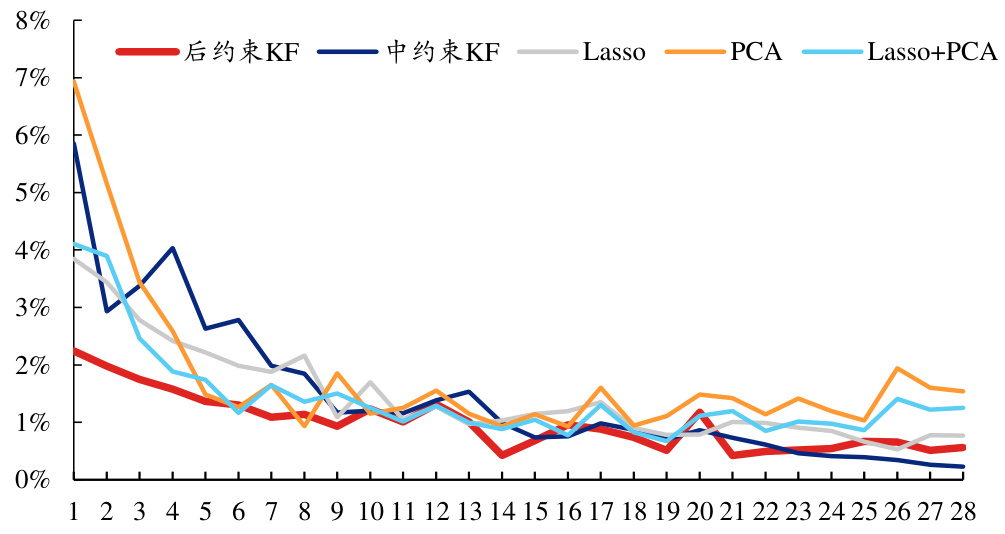
• 图表6：不同行业按重仓程度排序的估计误差均值

误差随仓位大小递减，且后约束KF在各个行业均显著优于其他方法，尤其在前三大行业误差降低40%-50%。这说明卡尔曼滤波在重点行业识别上的准确性极高。

• 图表7：前三大重仓行业不同方法误差明细

后约束KF误差分别为2.24%、1.98%、1.74%，显著优于Lasso+PCA（最高达到4.11%），进一步确认该方法的卓越性能。

图表综合结论： 通过充分利用时间序列信息和贝叶斯更新机制，卡尔曼滤波提高了仓位测算的动态响应性和准确度，特别对于重仓行业的估计效果有长足提升，对投资决策和机构仓位跟踪价值极高。[page::11-13]

---

2.5 宏观数据实时预测中的卡尔曼滤波应用

• 宏观环境挑战： 原因包括数据发布时间错开、数据缺失、频率不统一（季度、月度）、数据维度大而时间序列较短，导致直接线性建模困难。
• 动态因子模型（DFM）结合卡尔曼滤波优势：

- DFM抽取经济中的少数隐含因子，解释大量宏观变量；
- 卡尔曼滤波动态更新隐含因子状态，处理数据缺失，适应高维异步非完整数据；
- 模型可以实时融合所有新信息，有效提升预测准确性。

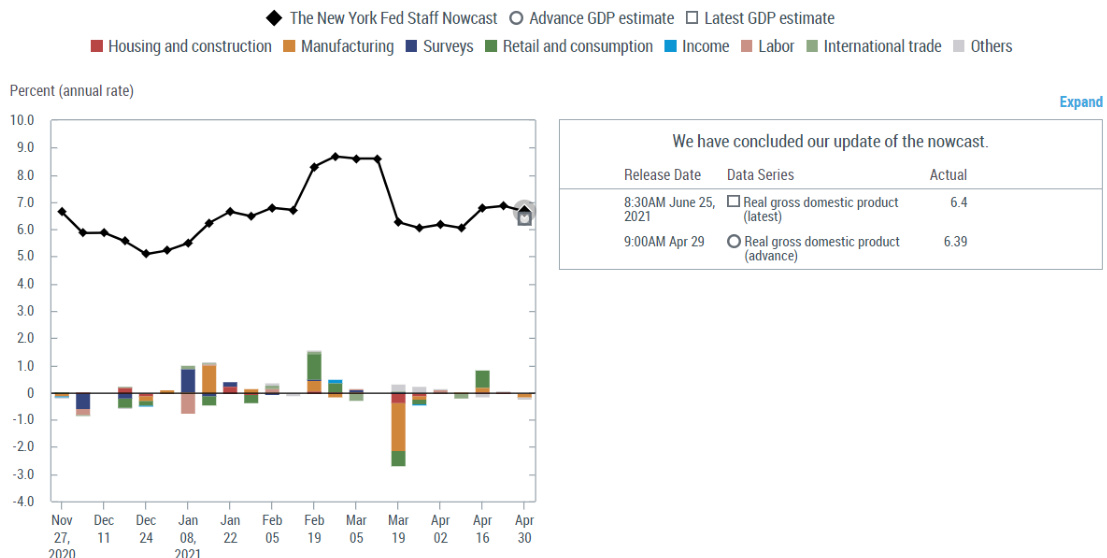
• 实际应用示例： 纽约联储的Nowcast模型，在2021Q1对美国GDP环比增速的实时预测中，随着多个数据点陆续发布，预测值不断更新，最终预测6.66%（非常接近实际6.4%），展示了模型的高效性和可靠性（详见图表8）。
• 技术细节：

- 应用状态空间模型形式
- 使用权重矩阵处理缺失数据，动态调整测量方程，保留非缺失数据贡献
- 通过卡尔曼滤波迭代，估计隐含因子，自动填充缺失宏观指标。

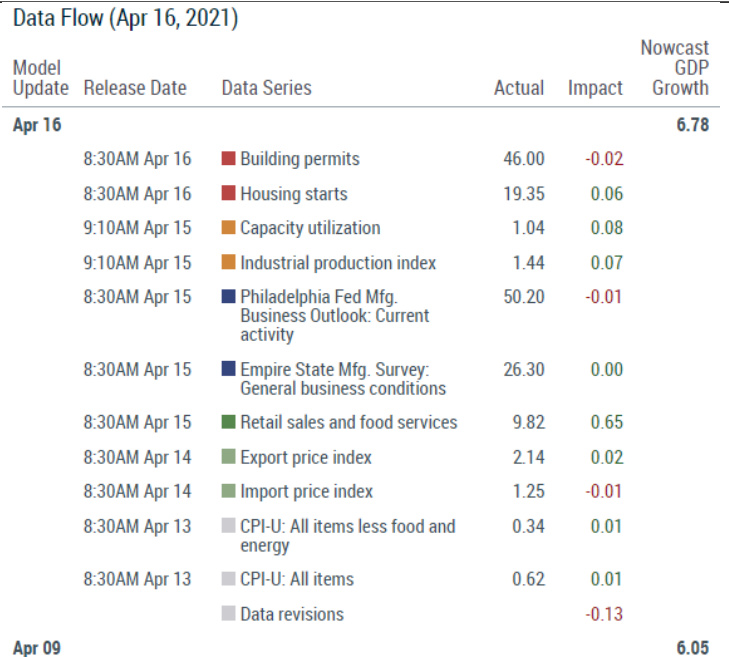
• 数据冲击分解： 通过比较不同数据版本下的预测结果，可以定量分析单个宏观数据对整体经济指标预测值的边际影响（“信息冲击”），这对于政策制定和投资判断尤为关键。纽约联储2021年4月16日数据发布情况示例显示零售销售等个别数据贡献了大部分预测修正（详见图表9）。
• 应用意义与局限：

- 该方法依赖于数据质量和更新速度，
- 边际变化的动态信息可能较绝对值更具投资指导意义。
- 体现了量化手段对经济数据的系统性融合和动态监测能力[page::14-16]

---

2.6 总结

• 卡尔曼滤波基于线性状态空间模型和贝叶斯思想，以递归方式实现受噪声影响系统状态的最优估计；

- 在基金行业仓位测算中把仓位视为时变隐含状态，通过动态调整基金收益率预测残差不断修正仓位，显著降低测算误差，特别是重仓行业误差降低约50%，优于传统线性回归和PCA方法，提升基金投资研究精度和机构动向捕捉能力；

• 在宏观经济建模中结合动态因子模型，卡尔曼滤波凭借其对异步缺失数据的优异处理能力，实现宏观经济隐含状态的动态估计与实时缺失数据填充，同时具备预测信息冲击定量分解能力，为政策制定和投资决策提供精准实用的实时经济信号；

- 除上述两大领域，卡尔曼滤波未来在基金久期测算、基金经理风格识别等金融投资领域具备广泛应用潜力，科研方向值得进一步探索。

---

3. 图表深度解读汇总

| 图表编号 | 内容描述 | 解读与意义 |
|------------|------------------------------------------------|----------------------------------------------------------------------------------------------------------|
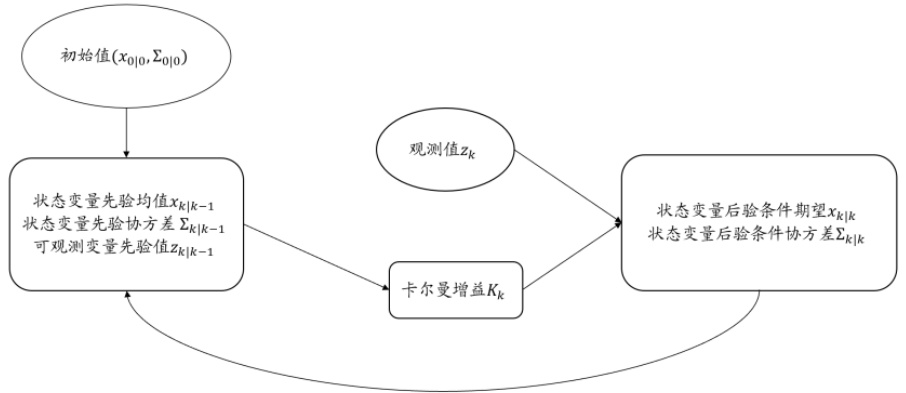
| 图表1 | 卡尔曼滤波计算流程示意图 | 描述了初始状态，状态先验预测和观测更新及卡尔曼增益的交互过程。体现状态估计的递归信息流逻辑。 |
| 图表2 | 2013至2021年每季度基金入选数量（只） | 样本规模逐年增长，覆盖范围广，保障实证的代表性和结果的可信度。 |
| 图表3 | 各方法基金行业仓位误差均值 | 后约束KF误差最低，表明卡尔曼滤波在准确性上明显优于传统方案。 |
| 图表4 | 各方法行业平均仓位误差均值 | 进一步验证行业层面误差减少，卡尔曼滤波在市场层面预测精准度提升。 |
| 图表5 | 2020年12月31日十大行业平均仓位测算对比 | 后约束KF行为与实际最接近，传统方法低估核心行业仓位，体现动态估计的优势。 |
| 图表6 | 不同行业按仓位排序的估计误差曲线 | 后约束KF在所有行业上误差较低，且在重仓行业降幅尤显著，表明该方法在关键行业的估计能力突出。 |
| 图表7 | 前三大重仓行业测算误差（多方法对比） | 后约束KF较传统方法误差降低达40-50%，验证方法有效性。 |
| 图表8 | 纽约联储2021Q1 Nowcast GDP环比预测示例 | 展示模型通过连续宏观数据发布调整预测的动态过程，展示卡尔曼滤波对GDP实时报送下预测修正的能力。 |
| 图表9 | 纽约联储Nowcast模型数据发布信息冲击分解示例 | 定量展示单只宏观数据对GDP预测贡献，突出模型的可解释性和预测动态调整透明度。 |

---

4. 估值分析

本报告并无针对企业或资产的传统估值模型分析内容，主要聚焦于计量方法应用与精准度提升，故无DCF、市盈率等估值方法涉及。

---

5. 风险因素评估

• 模型风险： 报告末尾明确提示模型基于历史数据，面临市场环境变化可能导致模型失效的风险。理论上卡尔曼滤波依赖线性高斯假设，若实际状态转移或误差分布强非线性非高斯，性能会受限。[page::17]
• 数据质量与时效风险： 宏观预测依赖数据更新和质量，延迟和错误数据会影响预测准确性。
• 约束处理局限： 估计过程中的约束处理方法（后约束和中约束KF）各有优劣，中约束方法在实证中表现不佳表明约束设计和迭代过程需谨慎把握。
• 潜在偏见： 卡尔曼滤波是一种统计型算法，忽视如基金经理行为变化、市场非理性波动等可能非量化因素，可能导致对仓位估计存在系统性偏差。

---

6. 批判性视角与细微差别

• 估计误差来源： 实证结果表明加入约束的中约束KF未达到预期效果，报告仅给出初步推测，缺乏更深入机制探讨，未来应加强约束条件设计与滤波稳定性研究。
• 算法适用性局限： 报告主打线性卡尔曼滤波，未涉及非线性扩展滤波（如EKF、UKF）及深度学习方法，对复杂非线性基金策略和宏观因子的适用性有限。
• 经济解释与模型假设： 虽然卡尔曼滤波可有效处理系统噪声，但其准确性依赖于模型参数(Q,R)的合理设定，这在现实投资中可能受到数据短缺或市场环境变化影响。
• 数据样本局限性： 实证集中于A股普通股票型和偏股混合型基金，缺乏对债券型、QDII和指数型基金的考察，结论的外推需谨慎。
• 宏观预测解读： 纽约联储Nowcast示例主要基于美国成熟市场数据，中国宏观经济数据的时效性和透明度问题未详细讨论，应用时需注意本土化调整。

---

7. 结论性综合

本报告系统性地介绍和运用卡尔曼滤波方法在基金行业仓位测算及宏观经济数据预测中的创新应用。通过详细数学原理说明和实证数据展示，报告显示卡尔曼滤波较传统基于线性回归的技术有显著优势：

• 基金仓位测算方面，卡尔曼滤波不仅实现了基金行业仓位的动态高频准确估计，显著降低了估计误差（重仓行业误差降约50%，行业平均误差降30%+），而且通过状态空间模型的动态更新机制，有效克服了传统方法平均化、滞后性和高估计噪声问题。

- 宏观经济数据预测方面，结合动态因子模型，卡尔曼滤波能够系统整合异步、缺失及高维度的宏观指标，实现对GDP等关键指标的实时精准预测。同时模型结构还具备分解单个数据发布对整体预测影响的功能，为宏观政策分析和市场判断提供量化支持。

• 报告中的图表详实展现了估计误差的具体数值优势及纽约联储模型的实际运行效果，为理论支撑提供了有力实证证明。

- 本文创新性地将经典控制理论中的卡尔曼滤波引入金融领域，展现出跨学科方法论的巨大潜力，并明确指出了未来在基金久期和经理风格评估等方面的应用前景。

整体而言，该报告为提升机构持仓估计和宏观经济预测的精准度提供了科学且高效的技术路径，具有较高的实践指导意义和理论价值，为市场参与者和宏观政策制定者提供了有力工具支持。

---

参考文献出处

[1~4] 中的相关经典卡尔曼滤波理论论文及宏观因子模型最新研究详见报告末尾。

---

（全文所有引用均基于原报告所示页码以便后续核查）

---

标注示例：

本报告对卡尔曼滤波基本原理进行了系统讲解[page::2-4]，并基于该模型设计了基金仓位动态测算方法，实证显示后约束卡尔曼滤波方法在重仓行业仓位估计误差上减少了约50%[page::11-13]；在宏观经济预测领域，结合动态因子模型，卡尔曼滤波能够有效整合异步缺失数据，实现GDP实时预测和信息冲击分解[page::14-16]。

---

附：主要图表展示（部分）

---

总结: 本报告逻辑严谨，技术详尽，实证充分，兼顾理论与应用深度，是卡尔曼滤波在金融投资和宏观预测领域应用的重要参考文献，具备极强的参考与推广价值。[page::0-18]

报告