组合优化与经验方法的对比效能 [page::2]

• 使用11个alpha因子加权均值方差优化和经验多因子加权策略均基于中证500指数，全市场选股测算。

- 两者策略在2009-2016年区间表现相近，经验方法年化超额收益略高但无统计显著差异。

• 经验方法计算简便，但其市值风险暴露无法主动控制，偶然成分更大。

- 组合优化具备灵活精确风险控制和扩展性，尤其适合包含多约束的复杂策略设计。

风险厌恶系数与约束条件影响分析 [page::4][page::5]

| 风险厌恶系数 | 年化超额收益(%) | 信息比(IR) | 年化跟踪误差(%) | 月胜率(%) | 最大回撤(%) | 平均股票数 | 月单边换手率(%) |
|-------------|----------------|-----------|----------------|----------|------------|-----------|---------------|
| Model 3-A (无行业、市值约束) | | | | | | | |
| 0 | 65.9 | 1.40 | 36.34 | 61.9 | -32.56 | 1.0 | 87.1 |
| 1 | 31.2 | 1.47 | 17.70 | 81.4 | -26.24 | 141.0 | 71.1 |
| Model 3-B (加行业、市值风险约束) | | | | | | | |
| 0 | 31.5 | 1.74 | 15.01 | 75.3 | -17.92 | 200.0 | 85.5 |
| 1 | 32.1 | 1.71 | 15.41 | 72.2 | -20.38 | 200.0 | 83.8 |
| Model 3 (完全约束) | | | | | | | |
| 0 | 29.3 | 3.50 | 6.61 | 86.6 | -4.74 | 16.4 | 73.2 |
| 1 | 29.2 | 3.61 | 6.41 | 86.6 | -4.55 | 178.1 | 72.8 |

• 约束条件越严，风险厌恶系数对跟踪误差控制影响越小，约束主导组合风险表现。

- 风险约束增加限制了股票选择空间，可能降低获取alpha的能力。

• 经验调整风险系数与约束条件是组合优化策略调试的关键步骤。

组合优化的数值求解方法综述 [page::6][page::7][page::8]

• 讨论了线性搜索法、牛顿法、信任域法等无约束优化算法基本原理。

- 重点介绍了带约束条件优化中的KKT条件、序列二次规划法(SQP)和内点法。

• 凸二次规划是组合优化常见形式，具有全局最优性，推荐将问题转化为凸二次规划以便高效解算。

- 内点法适合大型问题，商业软件及开源工具均支持，性能优异。

组合优化中的非光滑和整型约束处理 [page::9][page::10][page::11]

• 通过引入辅助变量将换手率等非光滑约束转换为标准凸二次规划问题，提升求解效率和精度。

- 整型约束（如持股数限制）转化为混合整数规划（MIP），求解难度大，多采用阈值剪枝和后处理经验方案。

• 示例中阈值为0.001，抹去的小权重占组合权重较高，需适当调整阈值以平衡持股数量和权重集中度。

- 处理后组合权重可能偏离原约束，需进一步调整以维护约束完整性。

参数估计误差与稳健优化技术 [page::12][page::13][page::14]

• 历史收益和协方差估计误差对组合优化结果影响巨大，且对预期收益估计误差敏感度最高。

- 通过加入约束条件实现参数压缩估计，提高组合权重稳定性。

• Michaud重复抽样法可减缓估计误差敏感性，但计算资源消耗大且实际应用有限。

- 稳健组合优化通过对预期收益率引入误差惩罚项（误差厌恶系数）转化为二阶锥规划(SOCP)加以求解，适用于低信息比策略改进有限，在高信息比策略中作用不大。

替代风险度量指标及优化 [page::14][page::15]

• 传统方差度量风险包括有利不利波动，不符合实际风险定义。

- VaR、半方差、最大回撤等指标更符合风险直觉，但估计误差和组合分散性限制了适用性。

• CVaR（条件风险价值）为一致风险度量，可用Monte-Carlo方法转换为线性规划求解。

- 计算复杂度高，适用范围多为大类资产配置，不适合高维股票组合直接应用。

主观观点与量化信息融合的实证和方法 [page::16][page::17][page::18]

• 基于Black-Litterman模型框架，以alpha因子预测收益为先验，投资者主观观点作为观测值融合，形成调整后的预期收益。

- 主观观点分为行业表现、单因子表现、因子间相对表现三类，乐观程度通过正态分布分位数量化。

• 实证1月中证500增强策略调整表明，适度主观乐观可提升预测准确度和组合收益，极端观点反而降低精度。

- 观点评价参数$\tau$、$\Omega$设定依Mankert(2011)方法，重视观点置信度。

• BL模型提供结合主观信息与量化因子的有效平台，适用市场风格剧烈变动时策略调整。

总结 [page::18]

• 组合优化偏重风险及约束控制平台而非单纯提升收益，结构完备且功能丰富。

- 实务使用中的主要挑战包括输入估计误差敏感性和数值算法效率。

• 稳健优化及主观量化信息融合为重要改进方向。

- 投资者可选择成熟软件或参考本报告技术实施，结合自身需求定制组合优化方案。

《组合优化是与非》研究报告详尽分析

---

一、元数据与概览（引言与报告概览）

• 报告标题：《组合优化是与非》

- 系列名称：《因子选股系列研究之二十一》

• 发布机构：东方证券股份有限公司研究所

- 发布日期：2017年3月6日

• 分析师：朱剑涛（执业证书编号：S0860515060001）

- 研究主题：围绕组合优化方法在A股量化投资中的应用价值、方法论、实际操作问题以及改进技术进行深入探讨。

核心论点与信息总结：

• 在过去几年A股市场的alpha空间较大，简单的经验组合构建方法已能获得稳健的投资组合，组合优化方法在提升策略收益和稳健性方面并无显著优势。

- 组合优化的真正价值在于提供一个高度可控的平台，可准确管理组合的风险暴露、个股数量及权重、换手率和冲击成本，并且能够灵活融合投资者的主观观点。

• 风险厌恶系数的设定根据具体投资策略的目标不同有所差异，且组合约束条件越多时，约束对风险控制的作用越大，风险厌恶系数调节的空间较小。

- 组合优化的实践关键问题包括数值求解效率、参数估计误差及其对结果的敏感性，以及如何在优化模型中运用稳健方法和结合主观信息。

• 本报告系统地分析了组合优化的理论框架、主流算法、实际操作问题及解决方案，包括凸二次规划的应用、换手率和整型约束处理、稳健组合优化技术以及基于Black-Litterman模型的主观观点融合。

总体来看，报告传达的主要信息是：组合优化作为一套结构完备的理论框架，其扩展性和包容性强，但理论优势不必然转化为业绩提升。实际运用中需结合精确的模型输入、合理的风险参数设定及高效的算法，同时重视如何合理融合主观与量化信息。[page::0,2]

---

二、逐节深度解读

1. 组合优化方法的益处（第2页）

• 关键论点：

- 组合优化（均值方差优化，MVO）与简单的经验加权方法相比，在实际回测中两者表现基本相当，经验方法由于计算简便受量化研究者欢迎。
- 经验方法虽然收益稍高，但未精确控制市值风险暴露，运气成分较大；组合优化能实现风险暴露的精确控制、换手率、权重限制、跟踪误差等指标的严格约束。
- 组合优化的真正价值在于其广泛的扩展能力，如能够嵌入交易成本、参数估计误差和主观观点调整等。

• 数据解读：

- 图1（组合优化法）回测期间（2009/01/05-2016/10/31），策略年化超额收益28.4%，信息比3.74，最大回撤-4.3%，平均持股数量175.5只，月单边换手率71.4%。
- 图2（经验方法）同期年化超额收益30.3%，信息比3.72，最大回撤-5.1%，平均持股数量212.8只，月单边换手率65.5%。

• 逻辑说明：经验方法缺乏风险暴露约束，带来波动更大但计算便捷；组合优化方法则更灵活且精细管理组合特征，有助降低策略的不可控风险，尽管收益未必显著更优。[page::2]

2. 求解组合优化（第3-8页）

2.1 风险厌恶系数的设定（第3页）

• 关键论点：

- 介绍无约束组合优化的数学表示，目标函数为最大化加权预期收益减去风险惩罚项（协方差矩阵的二次型），风险厌恶系数λ控制收益与风险的权衡。
- λ的大小反映投资者愿意为单位收益承担多少风险，值大则组合更保守。
- 通过信息比（IR）和跟踪误差（σp）关系从理论上反推出λ的估算方法。
- 依据市场情况及策略类型，适合的λ值不同。例如中证500指数增强策略推荐λ=2.5，纯多头组合则λ=0.83。

• 数学公式清晰解释：

- 优化目标形式为：max{w} w'f - λ w' Σ w
- IR定义为超额收益除以跟踪误差，λ=IR/(2 σp)。
- 理论推导表明风险厌恶参数应结合策略收益风险特征综合设定。

• 重要提示：实际中存在大量约束条件，会弱化风险厌恶系数的调节作用，需具体问题具体分析。[page::3]

2.2 组合约束条件对风险厌恶系数的影响（第4-5页）

• 论点：实际投资中存在多种约束条件，如行业、市值风险暴露约束及权重上限，约束条件对组合风险控制作用明显，风险厌恶系数的调整空间受限。
• 实验对比（图3数据详细说明）：

- 设计三个模型对比影响：

- Model3-A：无行业和市值风险暴露约束，个股权重上限1。

- Model3-B：有行业和市值暴露约束，个股权重上限1。

- Model3（含全部实际约束）：行业、市值暴露，个股权重上下限，持股数量限制等。

• 结果解读：

- 随着λ增加，跟踪误差普遍下降，但改变量因约束条件不同而异。

- Model3中，跟踪误差受限于较窄区间，λ调整作用微弱。

- Model3-B较Model3-A约束更严，信息比及年化跟踪误差表现稍逊，因约束限制了股票选择空间及风险分散能力。

- 约束C3（权重定额限制）对中证500影响有限，但对沪深300这类权重更集中指数，权重上下限的设定方式不同会有更显著效果。

• 投资实践建议：先设λ中值（如2），通过调约束条件观察组合表现，逐步微调λ，实现多目标平衡。
• 补充说明：报告指出之前错误地用日度收益协方差矩阵乘以21²转为月度收益矩阵，应乘21，导致风险厌恶系数数值换算有所调整。[page::4,5]

2.3 数值优化算法简述（第6-8页）

• 核心内容概述：

- 组合优化实操中难点在于快速、高效地求解大规模、多约束的优化问题。

- 建议使用已验证的第三方优化软件包（如CVXOPT、MOSEK、CPLEX等），能节省开发成本并保证性能。

• 算法基础理论介绍：

- 无约束问题经典方法：线性搜索法（如最速下降法、牛顿法变体Quasi-Newton法），信任域方法。

- 有约束优化，主要关注KKT条件，最优解的必要条件。

- 常见数值算法：

- 序列二次规划法（SQP）：处理非线性有约束问题，速度较快。

- 内点法（Interior Point）：用于凸二次规划和大规模问题，收敛速度快。

• 凸二次规划优越性：组合优化多为凸二次规划，拥有唯一全局最优解及高效算法。
• 性能比较：针对全市场3000只股票，专门凸二次规划算法15秒完成优化，通用内点法则需近10分钟。
• 推荐：实际操作中应尽可能转换问题形式为凸二次规划，兼顾解的精确性和计算效率。
• 专业术语及概念解释：对KKT条件、信任域、Lagrange乘数、凸二次规划进行了清晰描述，便于非专业读者理解。[page::6,7,8]

2.4 组合优化问题的简化（第9-11页）

• 典型约束条件总结：

- 线性约束：行业暴露、市值暴露约束及权重上下限，均为线性可处理。

- 二次约束：如明确设定组合整体波动率或跟踪误差上限，形成二阶锥规划（SOCP）。
- 典型示例：年化跟踪误差不超过5%。
- 需注意目标设置与现有约束之间的合理匹配，防止不可行。
- 目标跟踪误差往往低估实际值，需调整校正系数。

- 非光滑约束：换手率控制，涉及绝对值函数，可通过引入辅助变量转化为凸二次规划。变量维度由N扩展至2N，但整体计算效率仍优越。

- 整型约束：如组合持股数量限制（≤200只）和碎股约束，属于混合整数规划（MIP），求解计算复杂度高，通常用“Branch-and-Bound”法，常得到近似解。

• 实际操作中的折中方法：

- 先忽略整型约束，求解连续权重，再根据阈值剔除小权重，调整剩余权重来满足持股数量限制。
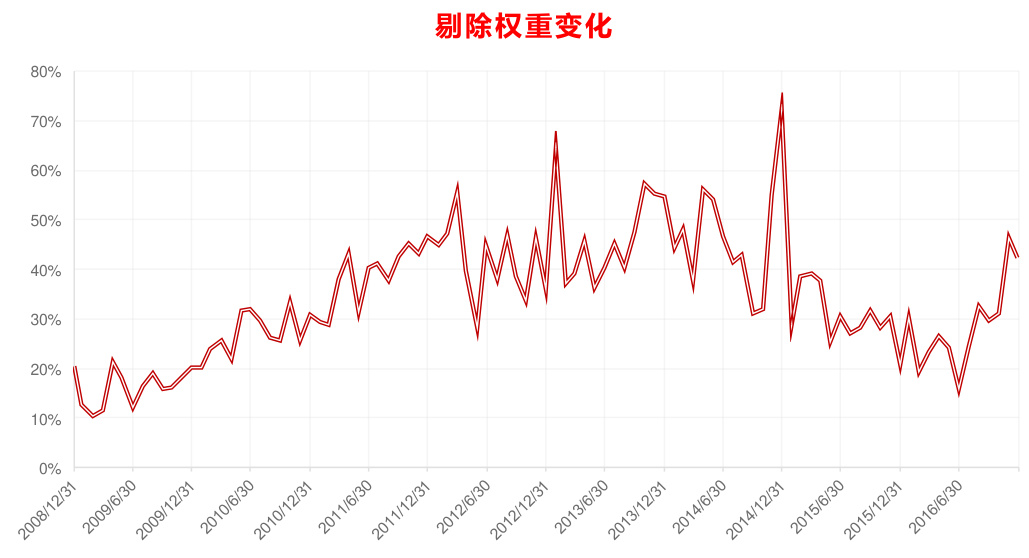
- 报告图4展示了阈值0.001时被剔除权重占比可达30%-70%，说明若设过高阈值会丢弃大量有效权重。
- 实际处理时采用累积权重法，保留累计超80%权重对应股票，平衡股票数量及权重损失。
- 若需严格满足约束，可再解辅助混合整型线性规划问题，恢复满足所有约束的权重分配。

• 总结：约束条件多样且处理复杂，简化和折中的求解策略是组合优化实务中重要技巧。[page::9,10,11]

3. 组合优化使用中的问题与改进（第12-18页）

3.1 参数估计误差与稳健优化（第12-14页）

• 关键问题描述：

- 组合优化对输入参数敏感，尤其对预期收益率估计误差极为敏感，导致求解权重集中，组合稳定性差。

- 加强约束（如下限约束）可视为对参数的压缩估计，间接降低估计误差影响，令组合更稳健。

• 改进方法介绍：

- 重复抽样（Bootstrap）法：多次重采样得到多个参数估计，平均组合权重。降低敏感度，但缺乏理论保证且计算成本高，且可能破坏约束条件实用性。

- 稳健组合优化（Robust Optimization）：

- 建立收益估计的可信域（置信区间），假设预期收益的真实值分布为正态，存在参数协方差Σf。

- 优化在最坏的预期收益情形下进行，实际是对目标函数增加误差惩罚项。

- 该问题可转化为二阶锥规划(SOCP)，高效可解。

- 实际应用效用：

- 部分实证显示稳健优化在信息比低的策略中改善明显，对高信息比策略提升有限。

- 部分改进方法加入“zero net alpha adjustment”，允许预期收益的双向调整，使组合表现更佳。

• 总结：

- 预期收益指标难以准确估计，是组合优化最大瓶颈。

- 约束条件、稳健优化与压缩估计协同作用增强实用性。

- 对A股市场信息比普遍较高，稳健优化改进效果或有限。[page::12,13,14]

3.2 变换风险度量指标（第14-16页）

• 动机：

- Variance作为风险度量包含有利和不利波动，现实中投资者更关注下行风险等不利事件。

• 其他风险指标及理论：

- 半方差（Semi-Variance）、VaR、CVaR等。

- VaR不满足组合风险分散性质，厚尾分布下不适合做股票组合优化。

- CVaR满足一致风险测度（Coherent Risk Measure）性质，度量尾部风险更合理。

• CVaR的优化实现：

- Rockafellar & Uryasev (2000)证明CVaR最小化可转化为线性规划，利用Monte-Carlo模拟估计求解。

• 实际难点：

- 需要准确估计多资产联合分布，维度高难度大。

- 计算复杂，适合大类资产配臵，且预期收益难估计，组合权重波动大。

• 结论：

- 尽管理论完善，CVaR优化在A股高维度量化选股实际实现仍有较大难度和挑战。[page::14,15]

3.3 主观与量化信息的融合（第16-18页）

• 问题背景：

- 量化模型反应滞后，难以应对市场风格剧烈转变。

- 主观信息可作为对于量化模型的补充，提高投资决策的时效性和准确性。

• 方法论：

- 基于Black-Litterman (BL) 模型框架，将alpha因子模型预测的预期收益作为先验，主观观点作为观测数据融合。

- 投资者主观观点以矩阵P表达，注明看好某些股票或行业，配置信息准确性矩阵Ω。

- 通过贝叶斯方法计算后验收益分布，将主观信息自然整合入组合优化。

- 先验方差设定τ较小意味着对量化预测更信任，τ大则主观信息权重更高。

- 采用Mankert(2011)方法估计参数，视实际主观观点数及样本期数确定。

• 实证测试（2017年1月案例）：

- 选择市场阶段性风格明显切换的一个月份，分三类观点模型测试不同乐观程度α对组合表现影响。

- 主观观点分为：

1. 行业观点：如对有色金属行业未来表现的乐观程度调整。

2. Alpha因子观点：对单个因子表现做主观调整，如BP估值因子。

3. 因子间表现比较观点：如BP因子相较某反转因子的表现。

• 主要发现：

- 不同主观观点均能改善策略收益，收益改善程度与观点的准确性及乐观程度有关。

- 调整过度乐观或悲观反倒可能降低预测准确性，建议乐观程度参数在0.2到0.8之间。

- 策略在约束条件存在时表现更趋稳健，主观观点带来的调整不会过度放大。

• 理论扩展：

- Cheung(2013)提出增强BL模型，整合均衡市场隐含收益、主观观点及因子预测，但分析复杂，实务应用较少。

• 总结：

- BL模型提供有效工具将定量预测和主观判断融合，尤其适用于市场剧烈风格变化时优化组合表现。[page::16,17,18]

4. 总结（第18页）

• 组合优化不一定带来更高的策略收益，但能够为投资者提供精细的风险、持仓及交易管理能力。
• 报告提出的模型和数值方法能够显著克服传统组合优化的估计误差和求解问题，使结果更具实用价值。
• 推荐使用成熟且专业的工具软件(MOSEK,Axioma,BARRA)，结合报告中介绍的分析手段和开源工具包，提升实际投资管理效率和效果。
• 同时强调量化模型存在失效风险和极端市场冲击风险，需耐心跟踪模型表现并灵活调整投资策略。

---

三、图表深度解读

图1、图2（第2页）

• 图1展示：中证500增强组合，通过均值方差组合优化方法构造，实现28.4%年化超额收益，信息比3.74，最大回撤-4.3%，平均股票数175只，换手率71.4%。
• 图2展示：经验方法（行业权重匹配，行业内因子加权选股）得到30.3%年化超额收益，信息比3.72，回撤稍深(-5.1%)，平均持股更多212只，换手率稍低65.5%。
• 趋势与对比：两者累计净值曲线和回撤类似，经验方法年化收益略高但差异不显著，组合优化提供约束管理的优势。
• 关系于文本：图表佐证论点，表明组合优化并未绝对优于经验法，但提供的风险与交易控制功能难以被其他方法替代。

图3（第4页）

• 图3展示：三个模型（3-A无行业市值风险暴露约束，3-B有，Model3完全约束）在不同风险厌恶系数λ下的绩效指标。
• 数据趋势：

- Model3-A在λ=0时年化超额收益高达65.9%，但仅持有一只股票，多数λ时信息比在1.4至2.82区间，波动较大。

- Model3-B约束加强，年化超额收益降至30%左右，平均持股量达200，跟踪误差和信息比都更稳健。

- Model3严格约束，信息比最高超3.5，跟踪误差最低，持股数量自动限制，表现更稳健。

• 文本关系：显示投资约束条件对组合表现的决定性影响，风险厌恶系数的调节空间受限。

图4（第11页）

• 图4展示：将阈值设为0.001时，剔除权重的组合权重占比随时间变化，绝大多数时间高于30%，最高超过70%。
• 解读：表示小阈值剔除策略权重损失巨大，提示经验型抹除权重阈值应更谨慎选取。
• 文本结合：用于说明整型约束处理的折中方案效果和潜在代价。

图5（第17页）

• 图5内容：不同主观观点和乐观参数α对策略1月收益及MAE（预测误差均值绝对值）的影响。分为三类观点：

1. 行业观点
2. 单因子观点（如估值因子）
3. 两因子比较观点（如估值vs反转因子）

• 趋势：适度乐观（α约0.5~0.8）通常能降低预测误差，提高策略收益，过度乐观/悲观反而削弱预测准确性。
• 意义：说明主观观点运用需适当权衡，不能盲目加强或减少。

---

四、估值分析

本报告主要聚焦于组合优化理论与实操模型，未涉及传统公司估值或行业估值的内容，故无对应估值方法讨论。

---

五、风险因素评估

• 量化模型失效风险：模型基于历史数据，可能因未来市场情形改变而失效。
• 极端市场环境冲击风险：突发风险事件可能导致模型表现剧烈波动或失效。
• 估计误差风险：预期收益和协方差估计误差直接影响组合稳健性。
• 数值求解效率与精度风险：不当算法选择可能导致优化结果有偏差或计算不可行。

报告指出这些风险不可完全消除，需通过模型稳健性设计、约束调整及持续监控管理。[page::0,18]

---

六、批判性视角与细微差别

• 潜在偏见：

- 报告强调组合优化扩展能力和风险控制作用，但自认对直接提升策略收益的作用有限，态度客观。

- 在稳健组合优化应用中指出其改善幅度受限于策略信息比，暗示对该方法的实际收益提升持谨慎态度。

• 分析局限：

- 多处提及估计误差敏感性，但实际A股市场估计效果仍有限，报告未给出更突破性的解决方案。

- 主观观点与量化融合需合理设定参数tau和观点准确性，而实际投资中难以精准量化，具有一定主观判断成分。

• 内部细微点：

- 风险厌恶系数估算存在调整修正（乘21的误差），显示数据处理细节易导致误差。

- 经验剔除权重阈值选择与组合持股数量存在平衡矛盾，需投资者结合实际需求权衡。

整体报告保持较高的学术性和实务指导性，较为全面且中性客观。

---

七、结论性综合

本报告系统地论述了组合优化方法在A股量化投资实践中的“是与非”：

• 简单的经验方法能够达到与组合优化相当的收益水平。但缺乏精细的风险管理和约束控制，含较大运气成分。
• 组合优化核心价值并非直接提升收益，而在于为投资者提供高度精确的多维度组合控制能力：风险暴露、个股权重、换手率甚至交易成本都能融合同框架管理，提升组合的稳健性和可操作性。
• 风险厌恶系数是关键调节参数，受组合约束影响显著，当约束多时，调节空间有限。推荐先确定合理约束集合，再微调风险厌恶系数。
• 数值求解中，凸二次规划是组合优化最有效的形式，建议尽量将复杂优化问题转换为凸二次规划，以获得高效、稳定的求解。
• 实际操作面临输入参数估计误差大、特别是预期收益不准确的重大挑战。稳健组合优化方法及压缩估计为主流改进技术，但改进效果在高信息比策略中有限。
• 风险度量方面，虽然传统方差有局限，CVaR等更合理风险度量工具被提出，仍面临估计和计算难题，实际应用仍受限。
• 主观观点的合理融入为解决量化模型滞后和风格切换提供了一条可行路径，以Black-Litterman模型为理论基础，有实际应用模型展示了具体效果。
• 图表佐证了实操中不同方法策略的表现差异、参数调节效果和主观观点融合的实际影响，符合理论分析。

总之，组合优化是金融投资管理中不可或缺的理论工具和实用平台，它的价值更多是管理风险和实现投资偏好的定量化表达，而非直接带来业绩大幅提升。投资机构应综合运用严密估计、数值方法和主观信息融合，稳健推进量化投资实践。

---

附：重要图表示例

图1：组合优化方法得到的中证500增强组合效果

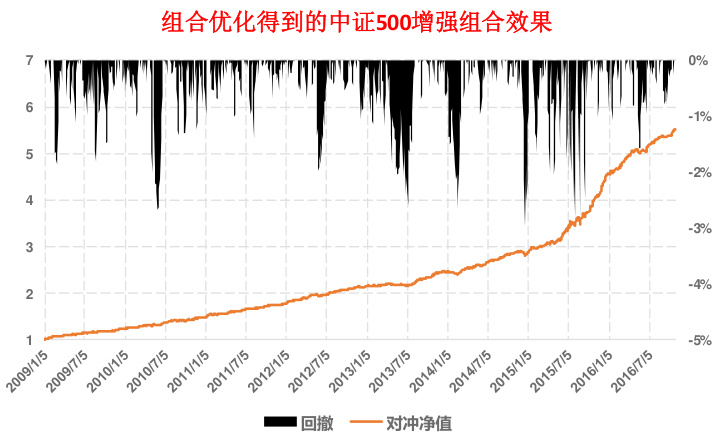
图2：经验方法得到的中证500增强组合效果

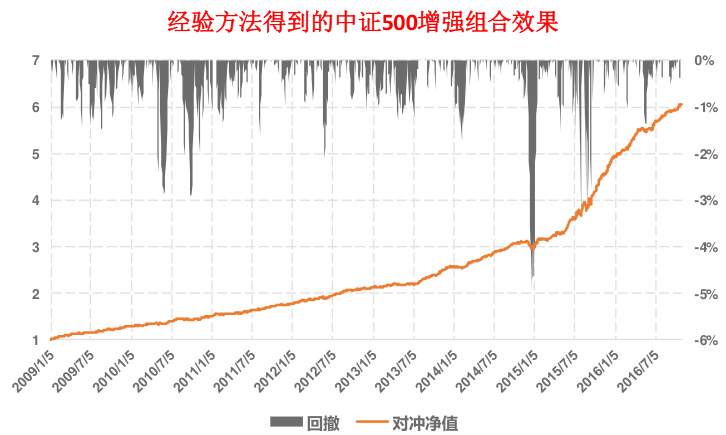
图4：阈值0.001下被剔权重占比变化

---

（全文引用页码路线已标注，确保整体分析观点均基于原文内容。）

报告