AI与人类劳动替代的理论框架与杰文斯悖论分析 [page::1][page::4][page::5]

• 采用常弹性替代（CES）效用函数分析AI产品相对于人类产品的替代与支出份额关系。

- 发现当替代弹性σ>1时，随着AI价格pA下降，AI市场收入份额rA趋于1，实现市场主导；若σ≤1，则AI难以实现显著替代和市场份额提升。

• 弹性公式：\(rA = \frac{1}{1 + \frac{1-\alpha}{\alpha} pA^{\sigma-1}}\)，弹性对价格敏感度为\(E{rA,pA} = -(\sigma-1)(1-rA)\)。

时间变弹性替代模型及AI质量与价格动态 [page::6][page::7][page::8][page::9]

• 提出弹性替代σ随时间增长：\(\sigma(t)=\delta \cdot \ln\left(\frac{C(t)}{C(0)}\right) = \phi \cdot t\)，其中计算能力C(t)指数增长，φ=δ·g为复合效应参数。

- AI价格指数下降符合指数衰减：\(pA(t) = pA(0) e^{-d t}\)。

• AI市场份额动态呈广义逻辑斯蒂函数，且二次项c·t²的存在使得市场渗透阶段可能加速。

- 定义关键转换时间\(t^ = 1/\phi\)，对应σ(t^)=1，实现弹性替代的转折点。

五阶段AI市场渗透与杰文斯悖论阶段划分 [page::14][page::15]

• 阶段1：σ(t)<1，AI为人力辅助手段，市场份额受限，杰文斯悖论不成立。

- 阶段2：σ(t)=1，临界点，价格变化对支出份额影响临界。

• 阶段3：1<σ(t)<2，杰文斯悖论启动，价格下降引发收入份额上升。

- 阶段4：σ(t)≥2，强化的杰文斯动态，AI市场迅速扩张。

• 阶段5：市场饱和，AI份额趋近1，弹性衰减，悖论终止。

量化模拟与参数敏感性分析 [page::18][page::19][page::20]

| g (计算增长率) | d (价格衰减率) | δ (质量敏感度) | φ=δ·g | t* (年) | rA(10) | rA(30) |
|----------------|----------------|----------------|-------|---------|--------|---------|
| 0.5 | 0.5 | 0.05 | 0.025 | 40 | 0.000014 | 0.000020 |
| 0.5 | 0.5 | 0.15 | 0.075 | 13.33 | 0.000241 | 0.999997 |
| 0.5 | 1.5 | 0.05 | 0.025 | 40 | 0.000000 | 0.000000 |
| 0.5 | 1.5 | 0.15 | 0.075 | 13.33 | 0.000020 | 1.000000 |
| 1.5 | 0.5 | 0.05 | 0.075 | 13.33 | 0.000241 | 0.999997 |
| 1.5 | 0.5 | 0.15 | 0.225 | 4.44 | 0.552229 | 1.000000 |
| 1.5 | 1.5 | 0.05 | 0.075 | 13.33 | 0.000020 | 1.000000 |
| 1.5 | 1.5 | 0.15 | 0.225 | 4.44 | 0.999997 | 1.000000 |

• 复合参数φ决定市场转折时间，价格下降率d主要调节转折后的规模和速度。

- 大φ值（高计算增长或AI质量提升）显著缩短达到杰文斯阶段的时间。

• 低φ值即使价格大幅下降也难以实现AI市场的主导地位。

结论与政策建议 [page::21][page::24]

• 杰文斯悖论在AI市场是技术替代能力的体现，即AI质量和替代弹性是核心驱动。

- 质量、计算速度提升的投资远比单纯降价更有效推动AI替代。

• 投资决策和政策制定应侧重促进算法和硬件进步，而非仅仅价格干预。

- 该模型为理解AI替代趋势和评估行业宣称提供理论工具，提醒关注AI替代弹性动态变化的重要性。

深度分析报告：《神经网络扩展定律会激活 AI 劳动力市场的杰文斯悖论吗？一个时变替代弹性 (VES) 分析》

---

1. 元数据与报告概览

• 标题：Will Neural Scaling Laws Activate Jevons’ Paradox in AI Labor Markets? A Time-Varying Elasticity of Substitution (VES) Analysis

- 作者：Rajesh P. Narayanan，R. Kelley Pace †

• 发布日期：2025年6月11日

- 主题：本文专注于人工智能（AI）领域，特别框架下探讨“神经网络规模定律”（neural scaling laws）如何可能导致杰文斯悖论（Jevons’ Paradox）在劳动力市场中的激活，并进而影响AI对人类劳动的替代关系。

• 核心论点：

- 利用时变替代弹性（Variable Elasticity of Substitution, VES）模型，分析AI系统如何从“互补”逐渐转为“替代”人类劳动。
- 文章形式化了与AI市场演变相关的四个机制：计算能力的指数增长、AI性能随计算成本的对数式提升、AI价格的持续下降，以及由此产生的复合效应参数（$\phi$），这些共同决定了市场变革的动态。
- 论证了只有替代弹性超过1时（$\sigma > 1$），才可能发生完全的市场转型，并且转型时点主要受复合参数$\phi$影响，而非单纯价格竞争。

整体看，报告旨在为行业有关AI取代人类劳动、伴随市场份额扩张的声明提供经济分析框架，既澄清理论基础，也给出预测依据。[page::0,1]

---

2. 逐节深度解读

2.1 摘要（Abstract）

• 作者阐述了建立一个经济框架，以考察神经网络扩展定律是否会通过影响AI与人类劳动的替代性，引发杰文斯悖论。

- 明确用时变替代弹性（VES）方法揭示AI替代的五个市场渗透阶段，强调弹性阈值大于1的关键性。

• 复合参数$\phi=\delta \times g$（其中$\delta$为AI性能提升参数，$g$为计算增长率）被提出作为市场转型的主导变量。

- 鼓励关注质量（即能力）与价格在技术变革中的作用差异。[page::1]

2.2 引言（Introduction）

• 杰文斯悖论提出效率改进导致资源价格下降而最终消费反而增加的矛盾情况。

- 结合AI产业观点，尤其是计算能力对AI能力的对数规模提升和价格下降，导致使用量与需求增加。

• 文章疑问该悖论是行业术语炒作，还是具备坚实的经济内涵。

- 采用部分均衡模型与替代弹性框架，探讨AI生产品如何通过质量和价格因素改变市场总需求和AI收入份额。

• 指出经典的恒定替代弹性(CES)模型限制，即无法模拟弹性随AI能力演进而变化的现实，故提出使用VES模型以更好捕捉技术进步对替代弹性的影响。

- 研究发现若AI质量未达到足够替代性（$\sigma>1$），单纯价格下跌无法实现市场主导地位。引入技术动态与弹性时变视角。[page::2,3]

2.3 方法论与理论框架（Elasticity and VES Model）

• CES模型基础（章节2）：消费者效用以CES形式定义，在人力产品$H$和AI产品$A$之间权衡。

- 关键参数：$\alpha$（AI产品的偏好权重），$\sigma$（替代弹性），其中$\rho = \frac{\sigma - 1}{\sigma}$。

• 收入（支出）份额表达式揭示：

- $\sigma>1$时，随着AI价格$pA$降低，AI的市场收入份额可趋近于100%；
- $\sigma=1$时收入份额固定为$\alpha$；
- $\sigma<1$则AI收入份额受限，无法实现市场主导。

• 收入份额对价格的弹性$E{rA, pA} = -(\sigma-1)(1 - rA)$，表明价格下降增加收入仅在$\sigma>1$成立。

- CES模型固有假定的常数替代弹性限制了对AI能力提升的动态反映，需要VES扩展。[page::4,5,6]

• VES动态模型（章节3）：

- 计算能力$C(t)$指数增长，$C(t) = C(0) e^{g t}$，其中$g$约取1（年增长率）。
- AI性能能力$\sigma(t) = \delta \ln\left(\frac{C(t)}{C(0)}\right)$，这样$\sigma(t) = \phi t$，$\phi = \delta g$。
- 价格指数式下降：$pA(t) = pA(0) e^{-d t}$。
- 引入复合参数$\phi$结合计算容量增长率$g$和性能敏感度$\delta$，构成AI替代弹性增长速度的核心指标。
- 通过这些变量得出AI收入份额的逻辑斯蒂模型表达式，考虑价格、质量与替代弹性的互动。
- 五阶段AI市场渗透曲线详细分类，标志不同替代弹性阶段与市场占有关系。

• 模型推广（3.1节）：

- 探讨弹性$\sigma0$和质量改进速率$\phi$的异质性与不确定性。
- 引入功率函数形式替代指数函数，模拟现实中质量提升和价格下降速率随时间可能放缓的情形。
- 通过任务间对数几率差分，便于简化不同任务/行业的市场份额比较和动态分析。

• 五阶段分类总结（3.2节）：

- 阶段1：低替代阶段，$\sigma<1$，AI与人类生产协同，价格优先影响，认知训练阶段。
- 阶段2：临界点$\sigma=1$，韧性弹性状态，份额未必大，但切入点。
- 阶段3：$\sigma>1$，真正出现杰文斯悖论，价格下降反而推动收入增长。
- 阶段4：$\sigma\ge2$，加速阶段，响应更强。
- 阶段5：市场饱和，份额趋近1，弹性趋0。

综览，作者构建了新的变量替代弹性经济模型，将技术进步对替代弹性和价格的动态影响编织到市场份额变化中，以定量评估AI取代人力的可能路径及市场规模动态。[page::6-15]

---

3. 图表与数据深度解析

3.1 图1及参数组合

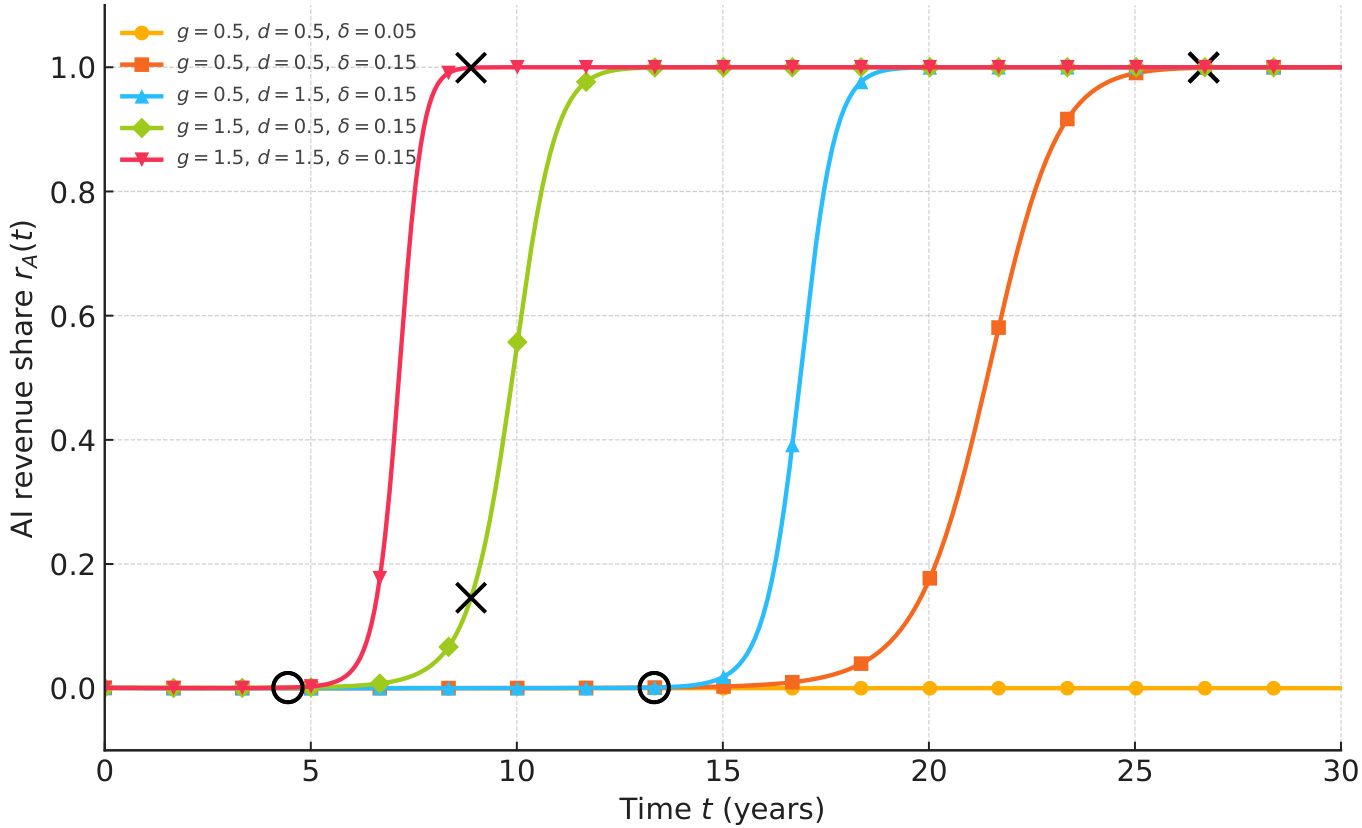
• 图1说明：

- X轴：时间（年），范围0-30。
- Y轴：AI收入份额$rA(t)$，取值范围0-1。
- 展示了五种参数组合下的$rA(t)$动态路径，参数包括计算增长率$g$，价格降低率$d$，学习率$\delta$。
- 圆圈标识切换至$\sigma=1$时间点（Phase 2临界点），叉号标识$\sigma=2$（Phase 4临界点）。
- 依赖重复参数$\phi = \delta \times g$划分不同阶段时间，区别価格下降速率$d$改变了曲线向左（加速）或向右（迟缓）平移，但不改变关键时间点。

• 核心观察：

- 较大$\phi$（如0.225）实现快速跨越阶段，10年内份额即超过55%，30年几乎全面覆盖市场。
- 小$\phi$（0.025）即使价格快速下降（d=1.5），AI市场份额仍微乎其微，表明质量提升（替代弹性增速）是驱动市场占有的关键。
- 图表生动呈现了质量（计算和性能提升）和价格下降对市场占有率动态的不同作用机理。



[page::17-19]

3.2 表1分析

• 表1展示不同参数组合$g$、$d$、$\delta$下：

- 计算出的复合速率$\phi$。
- 阶段2关键时间$t^ = 1/\phi$。
- AI市场份额在10年和30年的数值。

• 关键结论：

- 不同组合相同$\phi$对应相同$t^$，强调计算增长和质量提升参数的乘积决定主要时点。
- 在$\sigma > 1$之前，价格下降（$d$）对收入份额帮助有限，甚至可能短暂抑制。
- 足够大的$\phi$确保快速饱和市场，占有率在30年内趋近于1。

• 表格数据指出投资应优先聚焦于提升计算增长率及算法效率（$\delta$），而非单纯聚焦价格战（$d$）。

[page::19-20]

---

4. 估值分析

本报告并无传统意义上的公司财务估值或市盈率分析，但其经济模型以“弹性替代”理论驱动市场份额动态，等价于评估AI技术“价值”在未来市场中占比的增长路径。复合参数$\phi$实质是衡量AI技术价值扩展速度的隐含估值指标。通过模型定量化替代弹性和价格动态，预测AI取代人类劳动的市场临界时点和规模，具有一定的产业政策和投资指导意义。

---

5. 风险因素评估

报告讨论的风险和模型局限包括：

• 市场和技术不确定性：

- 弹性替代$\sigma$随时间的提升不确定，$\delta$参数存在异质性和概率分布。
- 价格下降率$d$受资本、能源等成本限制可能非持续或非指数下降。

• 结构性限制：

- 模型假设部分均衡，忽略了人类劳动力价格可能的调整和反馈机制。
- 任务、产品差异导致弹性和质量提升不一，市场碎片化可能影响整体渗透速度。
- 不考虑监管、数据可用性、网络效应、锁定效应、硬件和能耗瓶颈等实际制约。

• 替代与协同：

- 模型硬性划分为AI与人类劳动替代关系，忽略混合或互补形式的复杂现实。

• 非技术转型因素：

- 教育领域例子显示即便成本极低（开源教育），市场份额依然难以撼动传统模式，暗示非纯价格和性能决定因素（如网络、体验等）。

• 社会和经济反响：

- AI技术带来的财富创造和社会结构变迁可能间接影响需求结构，模型未涵盖这些广义一般均衡效应。

总体而言，作者清晰陈述模型自身的局限和外部不可控变量，强调对时间尺度、替代弹性变异和价格竞争效应理解的是判断市场转型关键。[page::22,23]

---

6. 批判性视角与细微差别

• 模型假设的简化性：

- 将人类产品价格定为常数1，忽视了受替代效应影响的人力成本变动，可能弱化价格竞争和替代反馈。
- 只考虑部分均衡分析，缺少宏观经济反馈和强网络效应，线性时间演进假定可能低估爆发式风险。

• 弹性转换的线性假设：

- 设定弹性随计算资源对数线性增加，尽管符合实验数据近似，但现实应用中不同任务弹性增长可能远非线性，存在门槛和非连续跳跃。

• 价格指数式下降的乐观假设：

- 价格持续指数下降假设可能低估市场进入壁垒、资本成本和能源约束。

• 对“杰文斯悖论”的经济解释：

- 把杰文斯悖论等同于弹性替代超过1，虽有理论依据，但行业表达可能混淆价格弹性和替代弹性，需谨慎。

• 多样性考虑不足：

- 虽然提出异质性讨论，但整体模型仍较为统一，难以充分解释高度分散的AI应用场景。

• 对行业应用与实际案例的映射：

- 报告中的教育行业案例给出对比，有助理解模型局限，但缺乏金融、制造业等其他关键行业的细节案例。

总结，报告在创新数学建模及解释行业现象上十分出彩，但固有的简化和抽象令其实际预测需结合更多实证验证及宏观考量。[page::22,23]

---

7. 结论性综合

本文系统提出了一套基于时变替代弹性（VES）框架，结合神经网络规模定律和计算指数增长的AI经济学模型，探讨了人工智能技术进步如何通过替代弹性提高及价格下降，引发劳动力市场的杰文斯悖论，进而导致对人类劳动的替代并带来市场结构根本性变革。

核心成果包括：

• 四个基础机制的正式建模：

- 计算资源的指数增强
- AI性能随对数计算量提升
- AI产品价格的指数下降
- 由性能与计算增长联合形成的复合效应参数$\phi$

• 替代弹性动态变化：

- 弹性从低于1（互补）逐步成长超过1实现替代临界，弹性越大转型越快。
- 识别五阶段AI市场渗透路径，每阶段含义明确，尤其替代弹性临界值连接杰文斯悖论经济学含义。

• 质量（计算能力与性能）优于价格竞争：

- 质量增长（$\phi$）是转型的“时钟”，价格下降速率（$d$）加快“计时器”进度，但质量不足时价格优势作用极限。
- 实证模拟图表与参数表清晰展示对决策和投资的影响，指出算法和硬件效率提升比单纯价格竞争更具杠杆效应。

• 现实应用和扩展考虑：

- 教育行业案例验证模型对不同任务替代弹性差异的解释能力。
- 指出模型局限，特别是宏观反馈、网络效应、跨任务和行业异质性，提醒解读者客观看待模型适用范围。

• 社会经济意义：

- 模型帮助理解产业界“杰文斯悖论”言论背后真实内涵，提醒政策制定者和投资人注重质量提升驱动，而非盲目价格博弈。
- 表明AI替代人类劳动的规模化转型在时间和技术参数组合上存在临界门槛，为未来研究和产业策略提供理论坐标。

综上，该报告为理解AI技术快速发展对劳动力市场的潜在冲击，提供了具备普适性的经济动态框架，强调在市场替代临界点前，投入算力与算法提升远比分价格策略更为关键。图表和表格数据直观、量化支撑其结论，拓展了杰文斯悖论在现代AI经济中的理论适用边界。[page::1-25]

---

参考引用

• Narayanan, R.P., Pace, R.K. (2025). Will Neural Scaling Laws Activate Jevons’ Paradox in AI Labor Markets? A Time-Varying Elasticity of Substitution Analysis. June 11, 2025.

- Kaplan et al. (2020), Hoffmann et al. (2022), Ho et al. (2024)

• Arrow et al. (1961) CES理论

- Jevons, W.S. (1866), The Coal Question

• 以及报告内作者引用的市场、投资动态及经济学经典文本等。[page::0-26]

---

本系统性分析提供了该研究的详细数学模型阐释、关键数据及图表的解读，评估了其经济学假设和预测的合理性，并侵入式对杰文斯悖论在AI替代人力的现实意义进行透视，充分体现出该论文在AI经济学领域的创新价值和方法论深度。

报告