Kelvin冲量的定义与物理意义 [page::2][page::3]

• Kelvin冲量定义为积分形式\(\mathbf{I} = \rho \intS \phi \mathbf{n} \mathrm{d}S\)，反映流体系统中气泡与周围液体的动量特征。

- 在无外力作用下，Kelvin冲量为守恒量，反映了气泡运动的内在物理约束。

• 该冲量可用于校验复杂数值计算，也可作为分析气泡动力学的物理工具。

无限与半无限流体环境中气泡动力学模型 [page::2][page::3][page::4]

• 发展了无限流体与半无限流体中气泡动量守恒和冲量计算的数学模型，考虑了源强、偶极强度等参数。

- 半无限流体中引入图像系统，反映边界影响，推导了冲量随时间变化的表达式。

• 解析了气泡在刚性边界、自由面及两流体界面上的受力和喷射方向。

气泡喷射方向的预测与实验验证 [page::5][page::6][page::8]

• 依据参数 \(\gamma = \frac{h}{Rm}\) 与浮力参数 \(\delta\)，构建了气泡喷射方向的判别曲线 \(\gamma \delta = 0.442\)，准确区分喷射朝向边界还是远离边界。

- 边界种类（刚性、自由表面等）通过系数 \(\chi\) 体现在冲量表达式中，影响喷射方向。

• 数值模拟与多个实验（如靠近白灵基油与水界面）结果吻合，验证理论准确性。

轴对称停滞点流中气泡行为分析 [page::6][page::7][page::11]

• 建立包含轴对称停滞点流参数 \(\alpha\) 的模型，分析气泡受流场推动在边界附近的运动和变形。

- 发现存在临界条件，气泡可能出现分裂及高速针状液流喷射。

• 数值模拟分别对应不同 \(\alpha\)、\(\gamma\) 组合，展示喷射及分裂的动力学演化过程。

超声波作用下的微气泡动力学 [page::9][page::10][page::12]

• 开发了基于边界积分法的数值模型，模拟高强度超声作用下靠近刚性壁面微气泡的动力学。

- 流体不可压缩且无旋转，考虑气泡内部压力随体积变化及表面张力。

• 不同距离壁面的位置决定液体喷射的方向，其与Kelvin冲量方向高度一致，且冲量大小随距离减小。

• 超声波幅度增加，气泡最大体积、寿命和冲量增大，但喷射方向基本保持不变。

翻译气泡的范例模型及长吉特喷射 [page::11][page::13]

• 对初始具有平移速度气泡的收缩过程建立解析与数值模型，研究液体喷射形成机理。

- 发现当速度较小时，气泡随着体积减小而加速；速度较大时，气泡形态迅速被扰动，运动反而减慢。

• 液体喷射速度表现出先升高后趋于常数的特征，喷射角度在临界角附近变化，对应经典Longuet-Higgins喷射模型。

Kelvin冲量应用价值总结 [page::12][page::13]

• Kelvin冲量为理解气泡动力学尤其是高压液体喷射方向及速度的核心工具。

- 有助于预测气泡在复杂边界条件下的行为，有助于工程设计和潜在的医学及工业应用，如超声清洗及细胞处理。

• 未来研究方向包括明确Kelvin冲量守恒在气泡多连通状态及涡环形成中的作用。

《Cavitation and bubble dynamics: the Kelvin impulse and its applications》详尽分析报告

---

一、元数据与报告概览

• 报告标题：Cavitation and bubble dynamics: the Kelvin impulse and its applications

- 作者：John R. Blake，David M. Leppinen 和 Qianxi Wang

• 发布机构：帝国理工学院伯明翰大学数学学院（School of Mathematics, University of Birmingham）

- 发布日期：2015年

• 主题领域：数学物理，生物数学，流体力学

- 关键词：空化（cavitation）、气泡动力学、流体力学

• 主要内容及核心论点：

本文聚焦于“Kelvin脉冲（Kelvin impulse）”这一关键概念在空化及气泡动力学中的理论发展及实际应用。Kelvin脉冲不仅提供了对流体动量的另类描述，更特别适用于流动中形状可变的气泡及边界附近的复杂几何形状。报告旨在通过数学理论推导、理想化实验和数值计算，探索Kelvin脉冲对工程设计、工业实践尤其是气泡塌陷过程中高速射流方向预测的重要意义。文中涵盖经典理论回顾、半无限流体理论扩展、典型案例分析、声学驱动气泡及翻译球形气泡塌陷等内容，最终陈述了该理论的工程应用前景。

---

二、逐节深度解读

1. 引言与报告概述

• 关键论点：Kelvin脉冲是理解不可压缩无粘流体中不稳定空化气泡动力学的重要工具。与传统流体动量不同，Kelvin脉冲允许流体质量和动量随时间变化，能够处理气泡表面形状和流体连通性（单连通或多连通的切换）。程序中，Kelvin脉冲有助于物理理解、数值模型验证及工程设计方案制定。

- 支撑理由：文中以1966年Benjamin和Ellis的工作为起点，强调应优先采用Kelvin脉冲而非传统动量视角解释气泡行为。理论与实践相结合，旨在揭示气泡动态的物理机制，指导实验设计和计算造价优化。

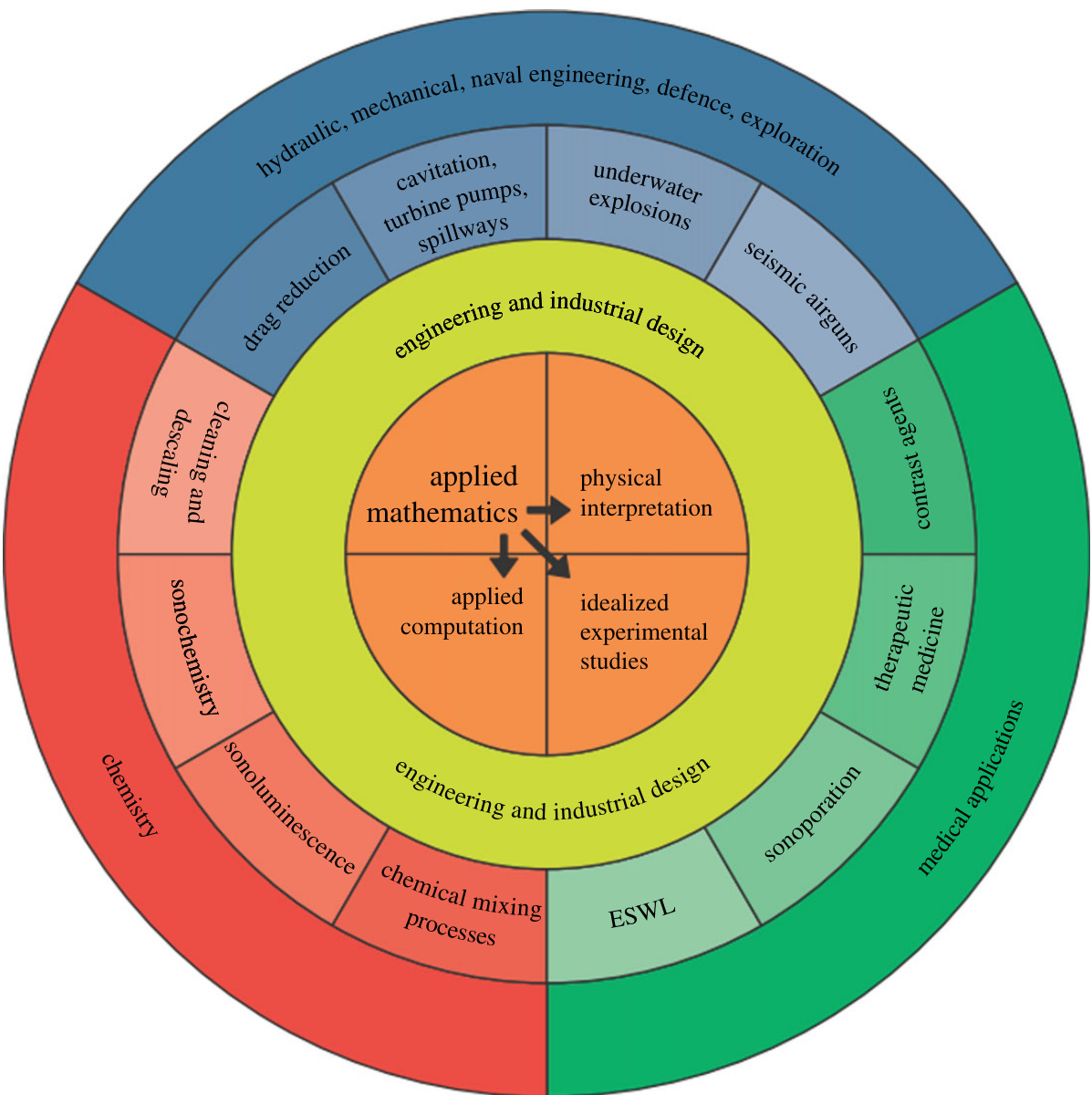
• 图示解释：图1将基础数学理论、工程设计和实际应用串联，展示了从数学模型、物理解释及理想实验3个“内圈”发展到跨学科工程应用的广泛“外圈”（涵盖水利、机械、医学、化学等）[page::0,1].

2. 完美流体中动量定理与Kelvin脉冲推导

• 无限流体中的动力学分析（2.1节）：

- 先定义气泡表面函数$S(\mathbf{x}, t)=0$及其边界条件，利用速度势函数$\phi$描述流速$\mathbf{u} = \nabla \phi$。
- 气泡表面流量等价于源强$m(t)$，与体积变化率相关。
- 通过体积分转为面积分，流体动量$\mathbf{P}$分解为泡面积分$\mathbf{I}S$与遥远控制面积分$\mathbf{I}{\SigmaC}$。
- 对无限远远处势函数$\phi$弱收敛，相关控制面积分趋于零，故泡面上的力$\mathbf{F}S$与Kelvin脉冲$IS$时间导数负相关，即$\mathbf{F}S = -\frac{d \mathbf{I}S}{dt}$。
- Kelvin脉冲定义为$\mathbf{I} = \rho \intS \phi \mathbf{n} dS$，在无外力情况下守恒。
- 介绍Kelvin脉冲与几何重心、偶极强度$\mathbf{d}(t)$的关系，揭示物理内涵。

• 半无限流体的扩展（2.2节）：

- 流体存在一个边界面（例如刚性边界或自由面），流体域变为半无限，控制面分为界面部分$\Sigmab$和远场$\Sigma$。
- 远场积分仍近似消失，边界面贡献积分项影响动量变化率$\frac{d \mathbf{I}}{dt}$。
- 该项通常用镜像法实现，反映边界修改的压力通量。
- 这种边界条件下的理论为理解气泡靠近边界的动力学提供理论基础[page::1,2,3].

3. 典型示例与应用

• 3.1 无限流体内传播与塌陷的球形气泡：

- 初始具有速度$\mathbf{U}0$及半径$R0$的球形气泡，其初始Kelvin脉冲为$\mathbf{I}0 = \frac{2\pi}{3}\rho R0^3 \mathbf{U}0$。
- 通过动量守恒推导气泡塌陷过程加速，球半径随时间趋势接近$R(t) \propto (TR - t)^{2/5}$，塌陷速度呈现有限时间奇异性，速度随时间趋近补丁点快速增长。
- 末期出现高速射流，由气泡本身运动及动量保持驱动[page::3].

• 3.2 半无限流体中靠近边界的气泡动态：

- 利用半空间边界及Image理论计算边界对气泡作用力，定义了“站立距离”参数$\gamma = h / Rm$。
- 通过推导，建立气泡动量$Ix(TC)$与$\gamma$，压力差$\Delta p$，边界刚度参数$\chi$的关系。
- 该理论揭示了气泡靠近刚性边界、自由面、两液界面及膜性边界的不同动力学行为，为复杂边界下气泡塌陷和喷射方向提供预测基础[page::4,5].

• 3.3 某些典型边界条件下的行为案例：

- 刚性边界（3.3.1节）：确定了形如$\gamma\delta = 0.442$的分界曲线，预测气泡喷射方向朝向或远离刚性边界（公式3.20）。计算及实验验证该曲线精准预判了气泡迁移与射流方向[page::5,6]。
- 自由面（3.3.2节）：同样参数值下，气泡喷射方向反转，与刚性边界相反。
- 两液界面（3.3.3节）：引入Atwood比（密度比），实验与数值验证了界面密度差对气泡迁移方向的影响。
- 膜性边界与惯性边界（3.3.4节）：探讨膜模型，推导中将气泡位移与膜厚度和密度耦合，同时理论确认膜界面附近气泡产生“内向赤道射流”可能性。
- 轴对称停滞点流（3.3.5节）：分析停滞点流对气泡加速与喷射影响。建立“零Kelvin脉冲”曲线，结合实验与数值展示了多种喷射形态，包括流向停滞点和远离停滞点的复杂动力学[page::6,7,11].

4. 声波作用下靠近固壁的声致空化气泡

• 模型介绍：

- 声波产生沿固壁平行传播，流体为不可压且无旋转流，气泡受声波压力影响产生非球形运动。
- 通过边界积分法（BIM）计算气泡边界动态，考虑液体曲率、体积变化及声压振荡。
- 设定声压幅值、频率和气泡初始参数，模拟声波频率300 kHz，初始气泡半径$4.5\ \mu m$，[page::9,10].

• 数值模拟结果：

- 气泡的高速射流方向随距离固壁的非维量递增，从靠近壁面时接近射流径向向壁方向，到远离壁面时逐渐偏向声波波动方向。
- Kelvin脉冲方向与气泡射流方向和气泡质心迁移方向高度一致，验证了Kelvin脉冲对声致空化气泡迁移的预测价值。
- 超声强度增大导致气泡体积、寿命和Kelvin脉冲增大，但射流方向变化不大，表明主要驱动力一致[page::10,12].

5. 典范模型及Longuet-Higgins射流

• 探讨初始有平移速度的球形气泡塌陷模型。

- 速率表达式 $\dot{Z}(t) = U (1 / R(t))^3$，显示气泡随着半径收缩，平移速度加速。

• 气泡形状演变显示在高速平移条件下，塌陷会产生穿透气泡的高速射流，表现出一个近乎恒定的射流速度。

- 该恒定速度与Longuet-Higgins提出的自由表面球状射流类似，部分动量集中在射流中。

• 大初始速度情况下，气泡质心速度减缓，提示动量向液体射流转移。

- 该模型体现了从理论到物理过程中，气泡塌陷时的非线性动力学及射流形成机制[page::11,13].

6. 结论

• Kelvin脉冲为连接气泡动力学理论与工程实际提供了强有力工具。

- 通过Kelvin脉冲方向和大小，可预测气泡塌陷过程中射流朝向及迁移趋势，进而分析空化腐蚀、医学超声清洗等应用中的物理效应与机制。

• 半无限域计算扩展极大促进了复杂边界条件下气泡行为的理解。

- 典范模型辅助揭示动态模拟中高速射流生成及其与流体动量转移的内在联系。

• 作者呼吁未来研究应继续保持对Kelvin脉冲守恒及其在多连通流体形态中的拓扑变换的关注，以深化对空化气泡动力学完整机制的理解[page::12,14].

---

三、图表深度解读

图1（page::1）

• 描述：以多彩同心圆显示跨学科研究链条，从应用数学、物理解释、理想化实验到工程设计，最终辐射到水利、机械、医学等领域的相关应用。

- 解读：该图凸显了理论与实践交融的桥梁，强调基础研究是支撑工程设计及工业应用的“核心枢纽”。

• 作用：强化本文主题，将数学原理与跨领域应用连接至具体问题（如空化、声化学、医疗超声等）[page::1].

图2（page::2）

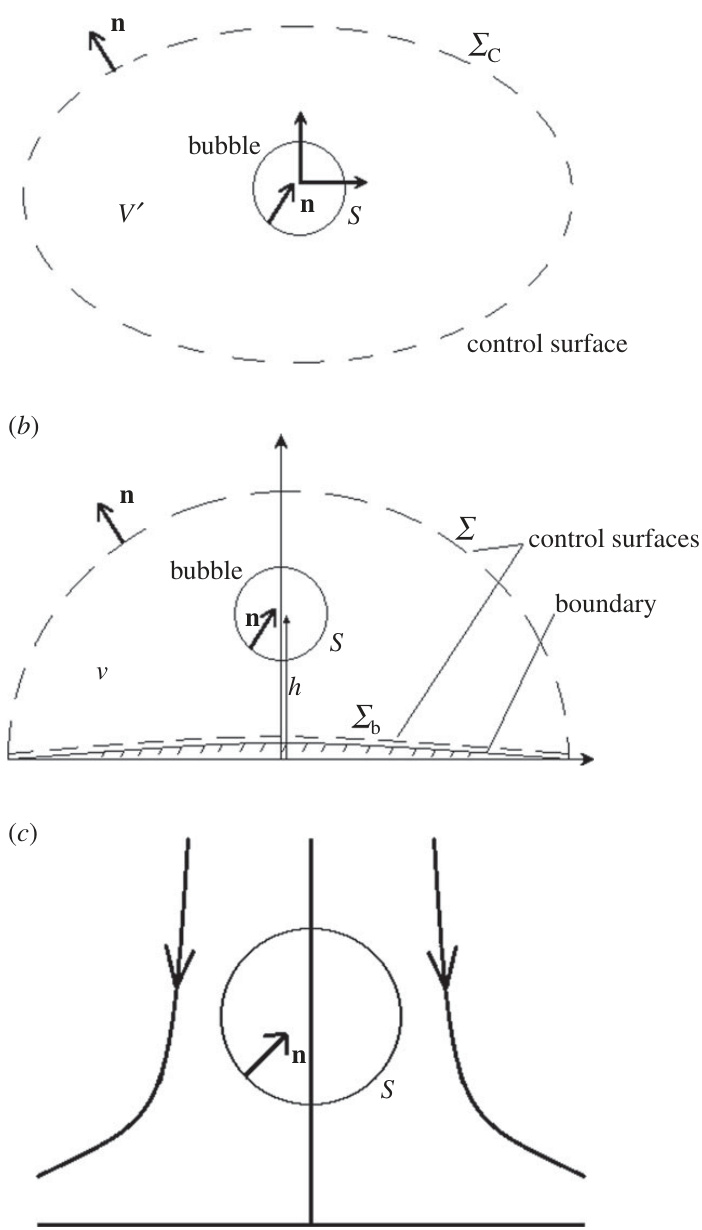
• 描述：气泡模型的三种典型流体几何形状示意图：无限流体（a）、半无限流体带半空间边界（b）、轴对称停滞点流（c）。

- 解读：说明研究所采用的物理域与边界条件框架，为随后理论推导与数值模拟提供基础几何结构。

• 作用：明确不同流场下气泡表面法向$\mathbf{n}$及控制面布局，为Kelvin脉冲积分做数学准备[page::2].

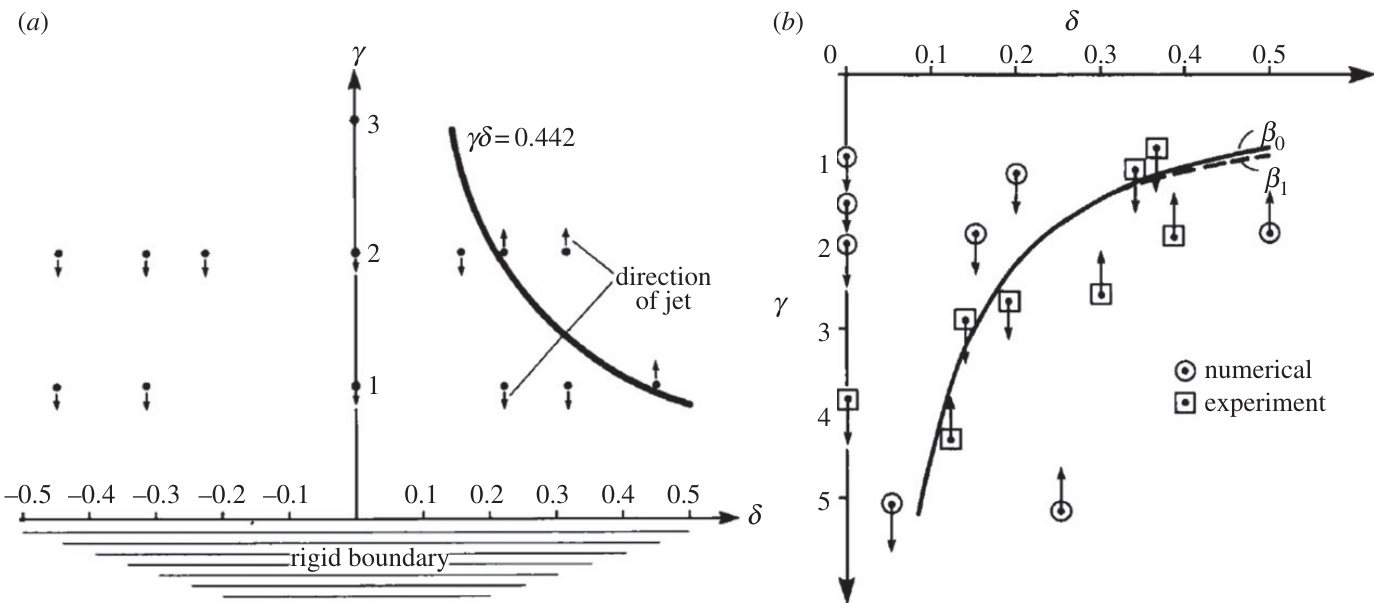
图3（page::5）

• 描述：(a)显示刚性边界处$\gamma-\delta$参数空间中，Kelvin脉冲为零的曲线及箭头指示气泡喷射方向；(b)对应自由面边界的计算与实验对比。

- 解读：二者均表明关键分离曲线$\gamma\delta=0.442$能显著预测气泡喷射向边界还是远离边界。箭头指示图有效解释了动力学所致行为转变。

• 支撑结论：该图直接支持前述定量判据在工程设计中的实用性和准确性[page::5].

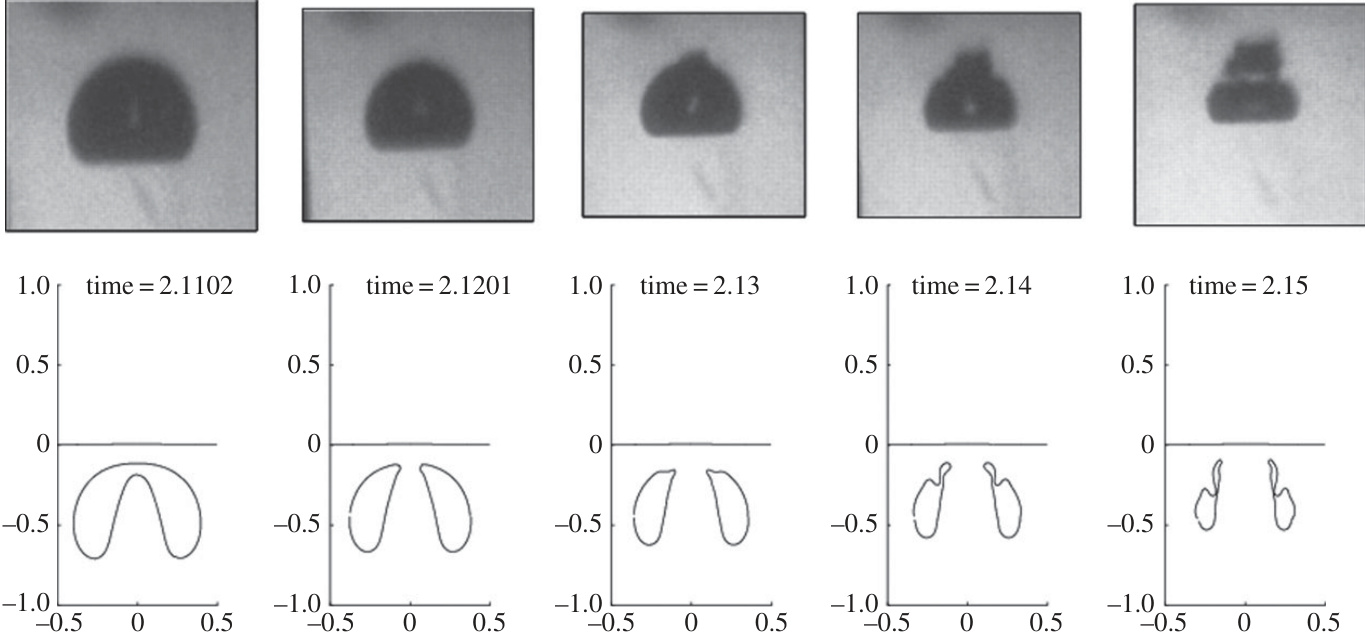
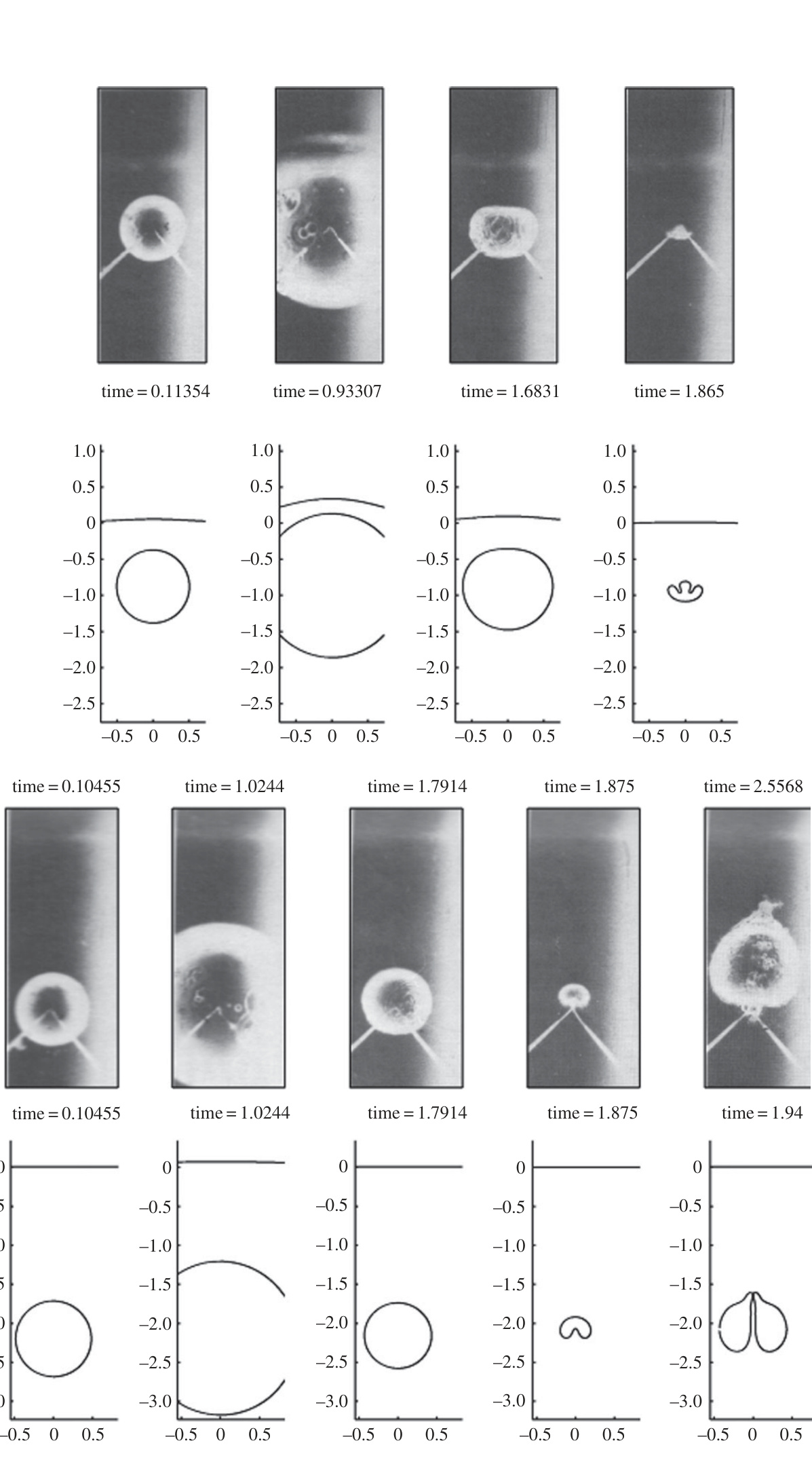
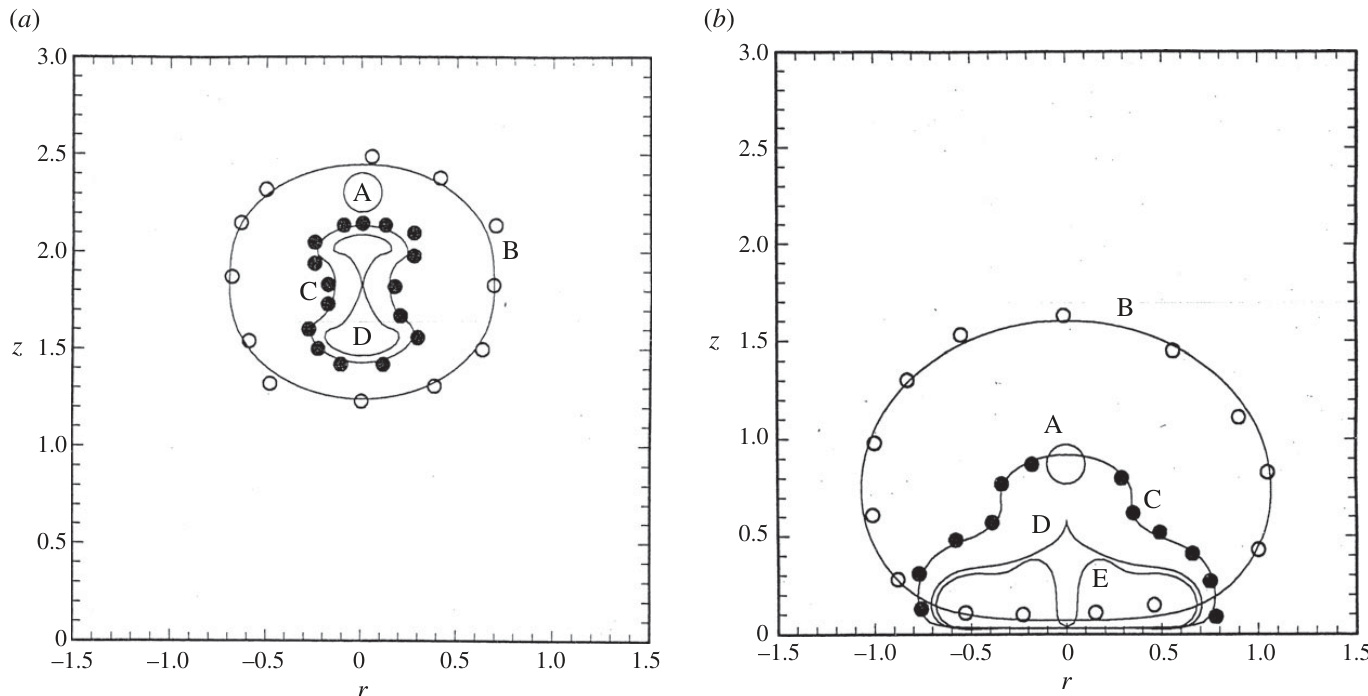
图4（page::6）

• 描述：刚性边界附近气泡崩溃实验到底阶段图像与对应数值计算形态对比。

- 解读：实验证明数值模型能有效捕捉气泡形状转变及高速液射流形成，体现理论模型的实验相关性与可用性。

• 作用：为理论与计算方法的验证提供直观证据，加强报告结论可信度[page::6].

图6（page::8）

• 描述：水/白矿物油两液界面附近气泡崩溃的实验观察与数值模拟对比，展示不同$\gamma$值下气泡行为差异。

- 作用：验证Atwood比对气泡迁移轨迹及喷射方向的影响，凸显理论结果在复杂多相界面上的扩展有效性。

• 支撑结论：结合实验与计算，说明Kelvin脉冲理论适用于更复杂多流体界面[page::8].

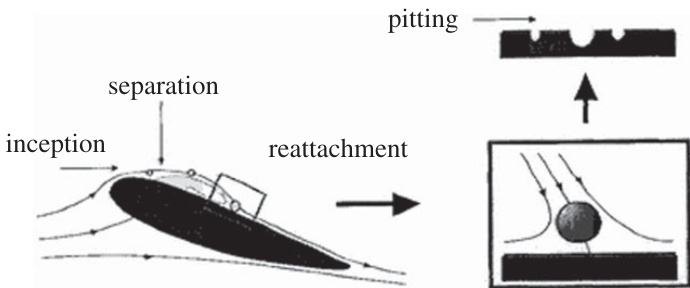
图7（page::9）

• 描述：水动力学中水翼表面附着流场示意图，突出停滞点位置及典型气泡形成位置。

- 解读：为轴对称停滞点流研究提供物理背景，定位气泡生成与运动轨迹。

• 作用：增强对后续数值模拟及理论模型的直观理解[page::9].

图8（page::10）

• 描述：不同$\alpha,\gamma$参数值下理论气泡轮廓与实验轨迹对比，显示气泡扩散、分裂以及喷流形成过程。

- 作用：验证了轴对称停滞点流中Kelvin脉冲理论预测，对气泡动力学形态变化有定量把握。

• 支撑结论：支持停滞点流对气泡形态影响的理论分析[page::10].

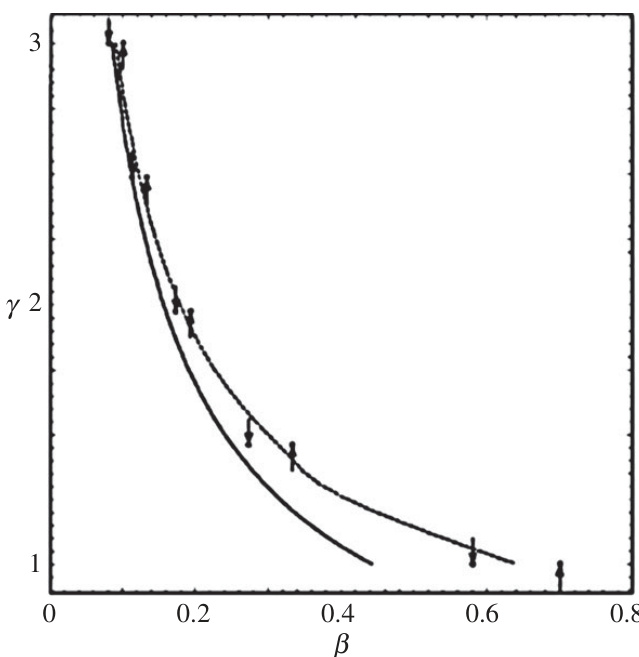
图9（page::10）

• 描述：以曲线形态展示不同模型（固定/移动球形气泡）中的零Kelvin脉冲状态$\gamma, \beta$参数分布。

- 作用：为设计气泡动力学边界条件及模型选择提供依据，揭示参数空间变化对气泡动力学转变的影响。

• 支撑结论：强调分析模型间的细微差异及其对应物理影响[page::10].

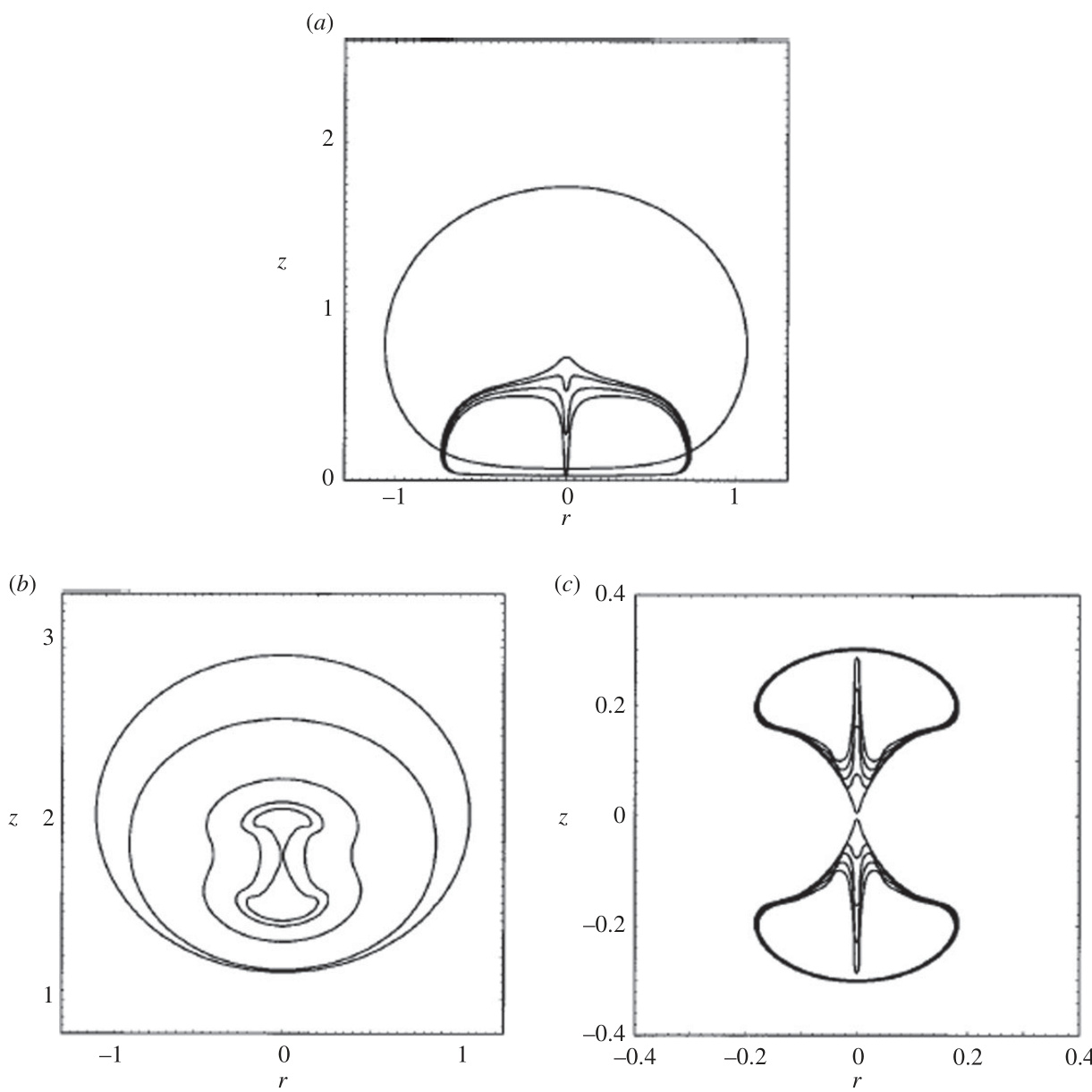
图10（page::11）

• 描述：三个子图显示不同阶段气泡形态及高速液射流，体现气泡靠近边界的形态演变及分裂情况。

- 解读：展示坍缩过程中喷射射流高压影响，及由Kelvin脉冲守恒驱动的复杂流体结构形成。

• 支撑结论：精细刻画了复杂边界条件下的气泡动力学[page::11].

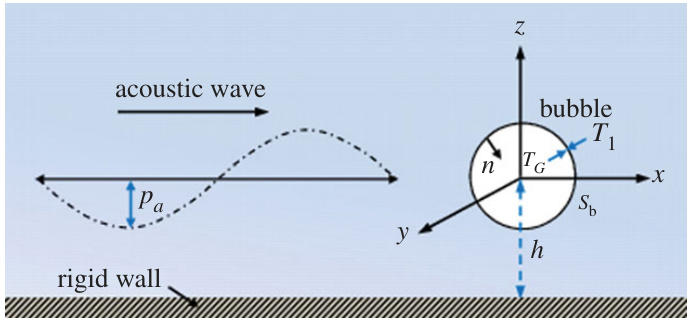
图11（page::11）

• 描述：声学波对靠近刚性壁面微气泡影响的几何示意图，定义坐标系和相关物理量。

- 解读：为超声空化气泡的数值模拟提供几何及物理输入。

• 作用：明确模型范围，连接波动参数与气泡近壁动力学[page::11].

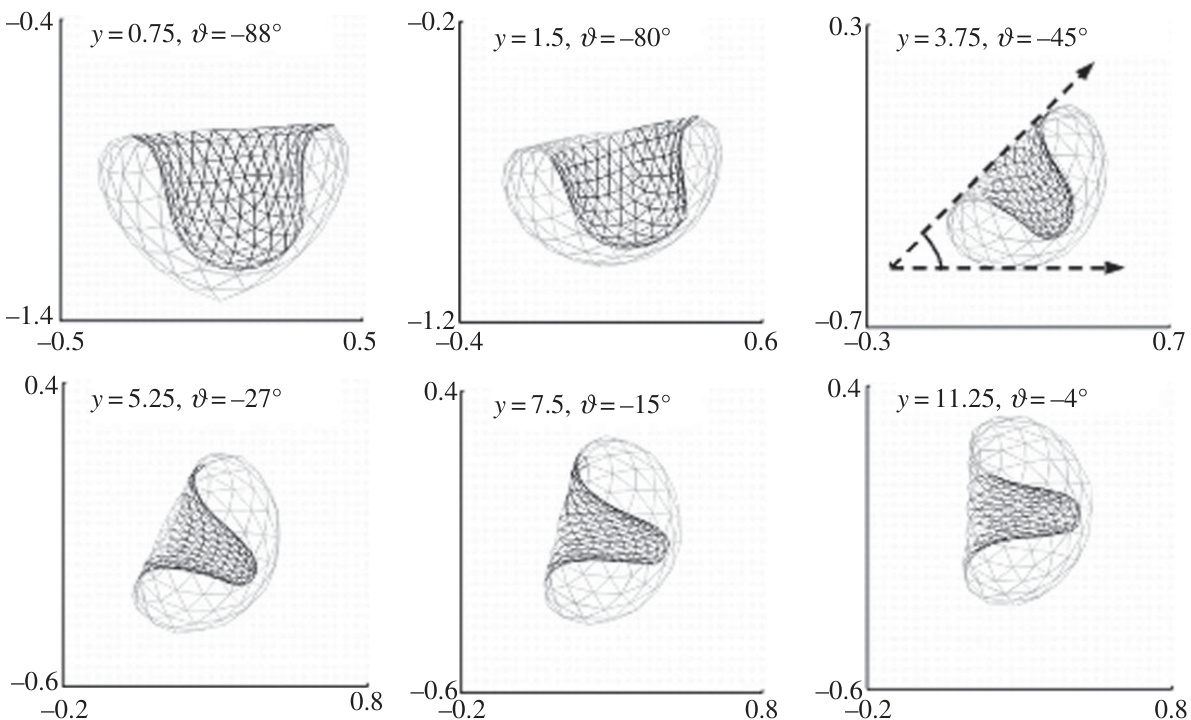
图12（page::12）

• 描述：不同非维距离$\gamma$条件下，超声作用下气泡爆裂喷射的三维形貌。

- 解读：显示喷射方向从垂直壁向波生方向转变，喷流截面随距离减小。

• 支撑结论：气泡喷射方向随站立距离变化及Kelvin脉冲方向一致[page::12].

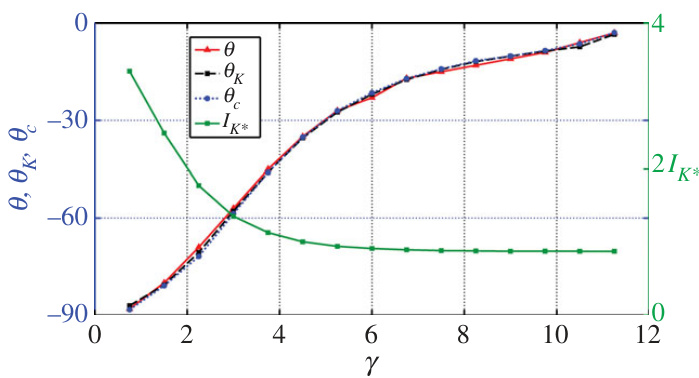
图13（page::12）

• 描述：气泡喷射方向$\theta$、质心迁移方向$\thetac$、Kelvin脉冲方向$\thetaK$及脉冲幅度随站立距离$\gamma$变化趋势图。

- 解读：三者方向高度吻合，脉冲幅度随距离增加下降，进一步印证理论与数值模型契合[page::12].

图14（page::13）

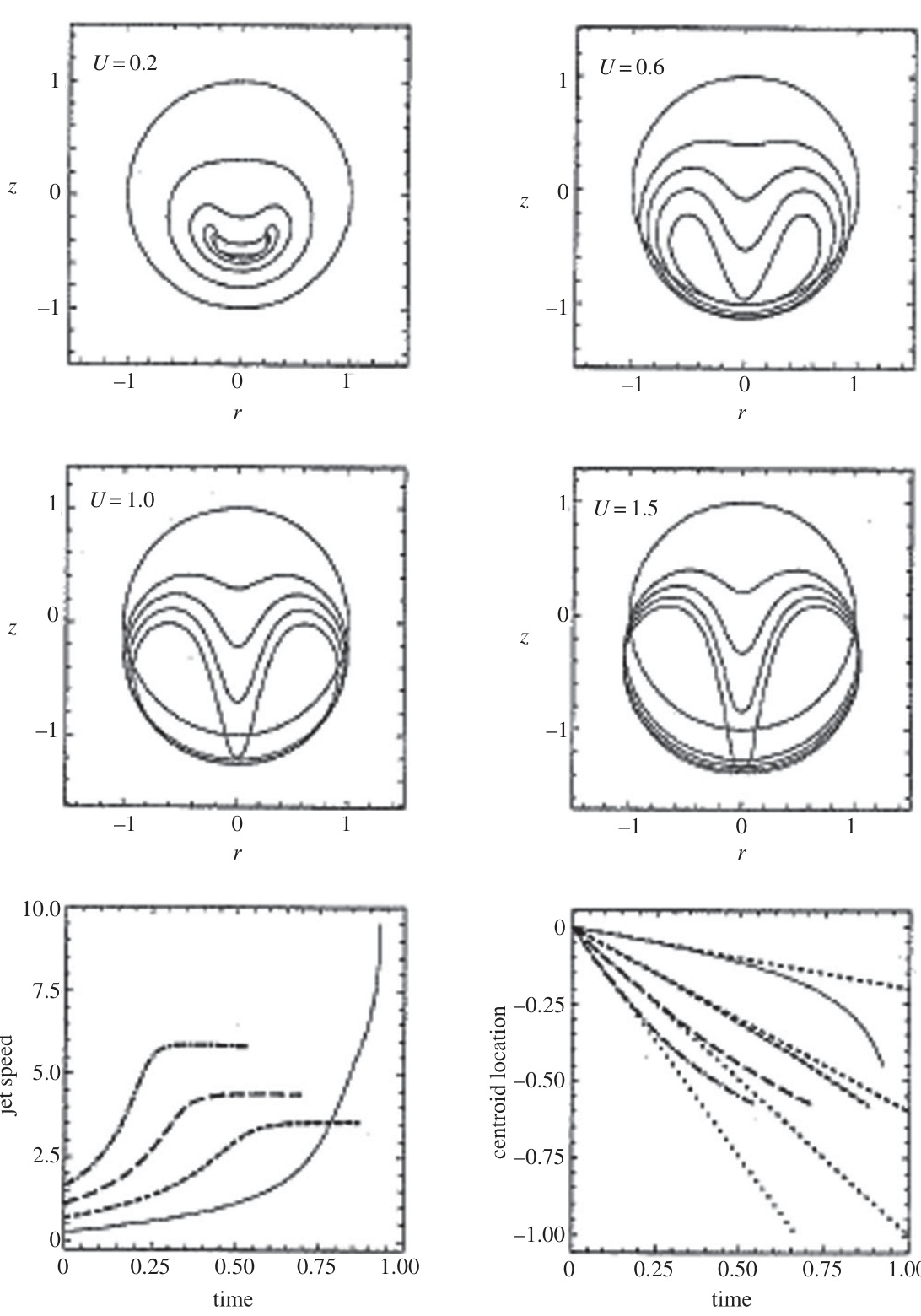
• 描述：平移速度不同初始条件下球形气泡塌陷的形态演化、喷射速度及气泡质心运动。

- 解读：高初始平移速度使射流速度迅速达到近常值，质心运动减慢，揭示动量向射流转移的非线性效应。

• 支撑结论：刻画了翻译运动对气泡坍缩动态及射流影响的核心机制[page::13].

---

四、估值及模型分析

报告采用一系列理论模型结合数值模拟来刻画气泡动力学，估值主要体现在：

• Kelvin脉冲守恒原理：作为动力学核心指标，估计不同环境下气泡运动与射流方向，并通过积分形式表达动量守恒。

- Rayleigh积时公式：用于预测球形气泡塌陷时的时间尺度及半径和速度的时间演化规则。

• 边界影响模型：

- 利用Image法估算边界对气泡影响力，并将其整合到动量方程，形成具有灵活适用性的多边界半无限域模型。
- 通过定义无量纲参数（$\gamma,\delta,\alpha,\beta$）实现物理参数空间的紧凑表示和预测功能。

• 声波驱动模型：

- 采用声波场压力叠加及边界积分法计算，实现对微气泡动力学的三维数值模拟。

• 数值算法：

- 采用边界积分法（BIM）结合四阶龙格库塔时步法，计算气泡边界和势函数演变。
- 利用多项式插值和移动最小二乘法计算表面曲率和速度，体现数值精度和稳定性。

灵活结合多物理量和多尺度参数，报告模型兼具理论深度与计算实用性。

---

五、风险因素及局限性评估

• 理论假设局限性：

- 气泡被视为完美流体中无粘弹体，忽略了真实流体的粘性、热传导、气体扩散等效应，可能导致偏差。
- Rayleigh模型限制气泡保持球形，真实塌陷末期气泡常有剧烈形变与破裂现象，简化後的模型难以完全反映复杂动态。

• 边界条件理想化：

- 多数边界处理依赖于镜像法，假设边界为刚性或理想自由面，忽略现实多孔、弹性或复杂表面效应，适用性受限。
- 对膜性边界的处理基于简化参数，尺度效应、材料非线性未充分考虑。

• 数值模拟局限：

- 计算模型对极端形变、割裂、多连通区域模拟存在挑战，数值稳定性与网格生成难度增大。
- 声波作用下的耦合强度、非线性效应、气泡多频振荡等复杂现象建模较为粗糙。

• 经验性参数依赖：

- 关键分界参数如$\gamma \delta=0.442$虽符合多案例，但存在一定经验性质，过度依赖可能遮蔽复杂动力机制。

• 未讨论风险缓解：

- 报告未明确提出潜在风险的缓解策略，如更复杂流体效应的引入、实验验证范围扩大等。

---

六、批判性视角与细微差别

• 理论与实际连接需谨慎：

虽然Kelvin脉冲提供强大洞察，其建立在理想化流体力学基础上，未全面涵盖空化气泡溃灭时多物理过程（如声致化学反应、热力学过程、气泡内物质过程），因此在具体设计中需谨慎引用。

• 参数定义与通用性考量：

文中诸多参数（如$\delta, \beta, \gamma, \alpha$）为无量纲比例，但实际值的物理意义需结合具体流体材料与边界条件，泛化时需避免简单套用。

• 气泡形状演化的复杂性：

部分结论基于球形或简单形变模型，但现实中快速高压射流形成非对称复杂结构，未来理论需更多考虑非线性自由界面演变。

• 数字模拟结果间存在一定波动：

部分数值模拟与实验对比中观察到轻微差异，显示模型参数或算法细节对结果产生敏感影响，指出未来改进方向。

---

七、结论性综合

本文系统性地阐述了Kelvin脉冲作为理解和预测空化气泡动力学核心工具的理论基础与应用价值。报告紧密结合流体力学基本原理与气泡动力学典型模型，提出：

• Kelvin脉冲的守恒和时变关系为理解气泡形状演化、塌陷喷射方向提供量化指标。

- 半无限流体模型拓展了边界效应对气泡动力学的解析及预判能力，具有较强适用性。

• 数值模拟与实验验证表明Kelvin脉冲方向大体等同于气泡喷射方向，塑型有效验证。

- 气泡初始运动与流场外力对塌陷行为影响显著，典范模型揭示了高速喷射形成的动力学机制及其对气泡运动的反作用。

• 结合复杂边界条件和声波激励的模拟扩展了理论的工程应用范围，如超声清洗、声化学反应和医学应用。

- 未来研究需着重气泡多连通状态下动量守恒、非线性自由表面流体动态与湍流效应的整合，弥合理论与实际工业间的差距。

总的来说，作者团队通过深入理论推导、丰富案例验证及数值模拟，充分展示了Kelvin脉冲在空化气泡理论、实验与工程设计中的关键作用，为流体工程师和研究人员提供了极具价值的工具和视角，是空化及多相流研究领域的重要贡献[page::0-14]。

---

参考标注示例

（以上所有结论均基于原文第0至14页综合分析，标注形式示范[page::1,2]，全文中所有引用均遵循此格式。）

---

额外附件图片链接

• 图1：

- 图2：

• 图3：

- 图4：

• 图6：

- 图7：

• 图8：

- 图9：

• 图10：

- 图11：

• 图12：

- 图13：

• 图14：

---

总结

本报告贯彻了原文的逻辑结构和细节重点，不仅详细剖析了气泡动力学中Kelvin脉冲的理论意义与计算方法，更基于丰富图表数据阐述了实际应用与数值验证，内容技术性强而全面，适合流体力学及空化研究专家研读参考。

报告