• 被动市场冲击建模创新 [page::1][page::3]

- 传统冲击模型多基于主动市价单，本报告提出的模型将冲击强度\(\kappa\)设为限价单簿的函数，反映大堆积量抑制价格变动的机制。
- 价格定义为未来市场订单预期的加权和，加权函数依赖于当前买卖侧限价量。对模型的数学严密性给出了充分条件（如\(\lambda^L, \lambda^C\)单调性及Hawkes过程稳定性）。

• 市场订单和限价单簿动态描述 [page::4][page::5][page::9]

- 主动买卖订单建模为独立的Hawkes过程，基线强度和自激核满足常见稳定条件。
- 限价单簿动态模拟基于非齐性Poisson过程，买卖双方的限价单和撤单以强度函数依赖于当前队列长度。
- 该模型允许队列长度暂时为负，但市场参数校准保证负值概率较低。

• 市场冲击定义及路径性描述 [page::7][page::8]

- 引入元订单(metaorder)作为限价单流入，形成改写后的排队动态。
- 路径性冲击定义为有无元订单时价格差异，解析表达为未来市场订单流加权差异的条件期望。
- 函数\(\kappa(\cdot)\)单调递减确保额外限价订单总是降低价格移动可能。

• 标度极限与长期行为分析 [page::9][page::10][page::13]

- 在标度极限下，Hawkes过程趋向结合Mittag-Leffler函数的非平稳波动过程，刻画活跃交易强度的长记忆特性。
- 排队深度和市场冲击过程重标度后收敛于确定性ODE+随机扰动的混合过程，包含市场波动的条件演化。
- 元订单强度在尺度\(T\)内等比例缩放，市场参与率对应强度函数\(f\)。

• 市场冲击近似与动力学特征 [page::14][page::15][page::16]

- 模拟展示市场冲击对参与率近似满足幂律，指数约为0.54，接近经典平方根冲击法则。
- 基于线性近似\(\kappa\)和队列动力差\(\lambda^L-\lambda^C\)，得到冲击的闭式表达：
\[
MIt = c\kappa \int0^t \int0^s e^{c\lambda (s-u)} f(u) du\, Ys^a ds + c\kappa \intt^\infty \int0^t e^{c\lambda (s-u)} f(u) du\, \mathbb{E}[Ys^a|\mathcal{F}t] ds.
\]
- 利用此公式，交易商可基于市场实时波动和订单流强度估算策略执行成本。

• 量化参数的统计估计分析 [page::18][page::19][page::20]

- \(\kappa\)作为单笔市价单冲击的量化参数，与价格波动率和Hawkes过程内生性密切相关。
- 提出基于高频离散化价格变动平方和和市场订单数估计\(\kappa\)的方法，支持线性回归扩展以纳入被动订单效果。
- 进一步引入\(\kappa\)对订单簿状态(限价量)的依赖，构建简化模型拟合\(\kappa^2(q) = a + b q\)，利用带权波动估计降低被动流动性对信息含量的影响。

• 被动市场冲击路径模拟 [page::17][page::19]

- 三条路径模拟展示市场冲击分为执行中阶段（单调积累价格阻力）和执行后阶段（波动驱动，冲击无显著衰减）。
- 说明被动限价单对价格的抵抗效应稳定存在，且冲击未表现出传统消散趋势，符合限价单簿快速稳定的认知。

报告题目与概览（元数据及引言）

• 题目：A theory of passive market impact（《被动市场冲击理论》）

- 作者：Youssef Ouazzani Chahdi、Mathieu Rosenbaum、Grégoire Szymanski

• 发布机构：未具体提及，时间为2024年12月11日

- 研究主题：本报告聚焦于金融微观结构中“被动订单”（即通过限价单执行的订单）的市场冲击机制研究，相较过去多数关注主动订单（市价单）的市场冲击，填补了被动订单市场冲击机制认知的空白。

• 核心论点：

- 传统交易模型通常假设每笔交易的信息含量固定，即单笔订单对价格的影响大小恒定。
- 本文创新性地提出该信息含量是可变的，依赖于限价单簿当前的可用成交量，建构联结流动性动态与价格变动的微观结构模型。
- 基于该模型，推导出被动Metaorder的市场冲击，获得闭式近似公式，具备实际应用价值。

• 主要贡献：

- 建立结合Hawkes过程和订单簿状态依赖信息含量的价格模型。
- 推导市场冲击的缩放极限，揭示大规模Metaorder执行下的长期市场冲击效应。
- 提供市场冲击函数形状和路径的解析近似，支持经纪人等实际操作使用。

• 关键词：市场冲击、Metaorder、Hawkes过程、高频数据、跳跃马尔科夫过程等 [page::0]

---

1. 引言深度解读

关键论点：

• 市场中交易者主要通过市价单（主动，立即成交）和限价单（被动，挂单等待成交）完成交易。

- 市价单承担流动性需求者角色，需支付买卖价差，且经常以metaorder形式存在（将大订单拆分为多笔连续订单），表现出长时间依赖性。

• 限价单方式虽避免立即成交风险，降低方向性风险，但传统上流动性提供者与流动性需求者角色逐渐模糊，算法交易根据市场实时状态动态选择投入限价单或市价单。

- 市场冲击定义为买单平均推高价格、卖单平均压低价格，是执行Metaorder主要交易成本之一。

• 文献表明非方向性（机械执行）交易的永久市场冲击非常小，有信息含量的交易冲击较大。

- 测量市场冲击存在噪声，需通过大量Metaorder数据平均化以揭示普适性规律。

• 实证发现市价单Metaorder价格随成交量增长呈凹形，达峰值后价格反向修正，且大宗交易冲击规模常近似服从成交量平方根规律，小单则呈线性。

作者推理基础与背景：

• 采用Hawkes过程描述市场订单流的脉冲自激特性，基于现有研究建立市价单市场冲击动态。

- 讨论市场冲击在机械与信息交易中表现差异并指出传统恒定冲击假设的局限。

• 强调现实中订单簿状态对市场后续价格变动具有预测能力，尤其在限价单成交时的影响[page::1]

---

2. 新微结构价格模型解析

2.1 价格模型构建

• 模型假设：

- 买卖双方市价单订单流至双方分别独立的Hawkes过程\( N^{a}, N^{b} \)，基线强度为\(\mu\)，自激核为非负函数\(\varphi\)。
- 限价单簿中的可用挂单量分别记为\( q^{a}, q^{b} \)，动态由限价单提交（\(L^{a}, L^{b}\)）、撤单（\(C^{a}, C^{b}\)）与市价单成交订单数量决定，且限价单和撤单分别为依赖队列状态的非齐次Poisson过程。
- \( L^{a}, C^{a}, N^{a} \)等六个过程由独立Poisson点过程驱动，跳时刻几乎不重叠，实现数学上的事件独立。
- 利用函数\(\kappa(q)\)，表示市场单对价格移动的贡献，该函数依赖当前挂单量，且假设\(\kappa\)单调递减，反映挂单量越大，成交推动价格的难度越大。

• 价格过程定义：

\[
Pt = P0 + \lim{T \to \infty} \mathbb{E}\Big[ \int0^T \kappa(qs^a) dNs^a - \int0^T \kappa(qs^b) dNs^b \mid \mathcal{F}t \Big]
\]

• 数学性质和存在性：

- 在一定条件下（如 \(\|\varphi\|{L^1} < 1\)，\(\lambda^{L}\)递减，\(\lambda^{C}\)递增，及价格贡献函数非负有界等）证明极限存在（见定理2.1）。
- 该模型推广了均匀冲击的经典Hawkes propagator模型，动态考虑了订单簿状态对冲击的影响。
- 价格表达式可写为对市价单成交的累积加权，权值动态调整。

• 模型含义：

- \(\kappa\)视为“价格阻力系数”，反映价格对市场单流入的抗拒度。
- 该构建应对恒定\(\kappa\)无法捕捉的限价单市场冲击方向及强度变化不足问题。

2.2 市场冲击定义及路径性

• 插入Metaorder：

- 以限价单形式执行的Metaorder由独立非均匀泊松过程\(N^o\)建模，叠加至原来的限价挂单数，调整对应Poisson强度。

• 路径市场冲击定义：

\[
MIt = \overline{P}t - Pt
\]

其中，\(\overline{P}t\)为含Metaorder挂单的价格过程。

• 解析表达：

\[
MIt = \lim{T \to \infty} \mathbb{E}\Big[\int0^T (\kappa(\overline{q}s^{a,t}) - \kappa(qs^a)) dNs^a \mid \mathcal{F}t \Big]
\]

• 性质：

- 由于\(\overline{q}s^{a,t} \ge qs^a\)，且\(\kappa\)递减，冲击为非正值，意味着被动限价单挂单增加能降低价格变动压力（推动价格朝相反方向），符合市场直觉。
- 实际计算复杂，依赖于多个跳跃过程的耦合，具有一定技术挑战性[page::4–7]

---

3. 缩放极限（Scaling Limits）

3.1 订单簿模型缩放极限

• 基本思路：

- 考虑交易时间尺度\(T\to\infty\)，对市场订单流（买卖双方为Hawkes过程）和订单簿状态进行适当时间及强度缩放，观察极限分布行为。

• 模型假设A：

- 自激核\(\varphi^T = a^T \varphi\)，带有某些渐近性质，保证序列\(a^T \to 1\)，且\(\|\varphi\|{L^1}=1\)。
- 设定多种参数收敛，确保弹性临界行为，顺利刻画长记忆和粗糙性特征。

• 过程重标定：

- 订单计数及强度依据比例\(T \beta^T\)缩放，形成近似有界的过程序列。

• 极限过程特征：

- 极限为具有随机驱动力的连续过程，包含刻画记忆特性的Mittag-Leffler函数成分，反映了市场的粗糙波动性\[Yt\]。

• 订单簿大小变量极限：

\[
\hat{q}t^{x,T} = \frac{1}{T\beta^T} q{t T}^{x,T}
\]

过程收敛到满足ODE的连续过程：

\[
qt^{x\prime} = \lambda^L(qt^x) - \lambda^C(qt^x) - Yt^x
\]

其中，\(Yt^x\)动态描述减去市场无序波动带来的影响，表明订单簿是确定性条件下基于随机市场波动的动态过程。

• 特例：若\(\lambda^L - \lambda^C\)为仿射线性形式，ODE解析解为卷积积分形式，方便实际模拟和分析。[page::8–11]

3.2 市场冲击缩放极限

• Metaorder缩放假设：

- Metaorder的限价订单流\(N^{o,T}\)被设为非齐次泊松过程，强度依参与率函数\(f\)缩放。

• 缩放后市场冲击定义：

\[
\widehat{MI}t^T = \frac{1}{T \beta^T} MI{tT}^T = \mathbb{E}\Big[\int0^\infty (\kappa^T(\overline{q}s^{a,T,t}) - \kappa^T(qs^{a,T})) d \widehat{N}s^{a,T} \mid \hat{\mathcal{F}}t^T \Big]
\]

• 函数\(\kappa^T\)假设：

- 存在Lipschitz函数\(\kappa\)，满足重新标度关系 \(\kappa^T(x) = \kappa(x/(T\beta^T))\)。

• 极限定理（3.6）：

- 对任意固定\(t\)，\(\mathbb{E}[\widehat{MI}t^T]\)收敛至

\[
\mathbb{E}[MIt] = \mathbb{E}\Big[\int0^\infty (\kappa(\overline{q}s^{a,t}) - \kappa(qs^a)) Ys^a ds \mid \mathcal{F}t\Big]
\]

• 积分表达中，\(\overline{q}^{a,t}\)与\(q^a\)满足带有Metaorder强度包装的微分方程，代表限价单对订单簿容量的动态影响，\(Ys^a\)为市场即时方差（波动率）。[page::12–13]

---

4. 应用与市场冲击近似

4.1 市场冲击的渐近形态

• 假设：

- 令 \(D = \lambda^L - \lambda^C\) 为可逆函数，且市场即时方差\(Y^x\)处于平稳态，常数为\(m\)。
- 参与率函数\(f(t)=\gamma\)为常数，代表稳态Metaorder执行强度。

• 解读：

- 原订单簿平稳点为\(q^ = D^{-1}(m)\)。
- 有Metaorder时订单簿平稳点为 \(\overline{q}^ = D^{-1}(m - \gamma)\)。
- 市场冲击近似为

\[
\kappa(\overline{q}^) - \kappa(q^) = \kappa(D^{-1}(m-\gamma)) - \kappa(D^{-1}(m)).
\]

• 特殊情况与分析：

- 若\(\kappa\)常数，则无市场冲击。
- 若\(\kappa\)和\(D^{-1}\)均为线性，故整体市场冲击近似线性，表示小参与率下冲击线性增长。
- 大参与率极限时，假设订单簿有线性回复力，且\(\kappa\)与价格移动阻力关系类似于平方根函数，关系如下：

\[
\kappa(\overline{q}^) - \kappa(q^) \approx -\sqrt{c \gamma}
\]

近似符合经典“成交量平方根冲击”经验定律。

• 数值模拟：

- 采用特定形式\(\kappa(q) = c1 \sqrt{\log(e^{-c2 q} +1)}\)并设置线性流动性响应，10000次模拟重现了市场冲击幂律行为（拟合指数约为0.54），与理论推断吻合。

• 图1：市场冲击随参与率变化的幂律拟合曲线，显示逼近平方根函数特征。

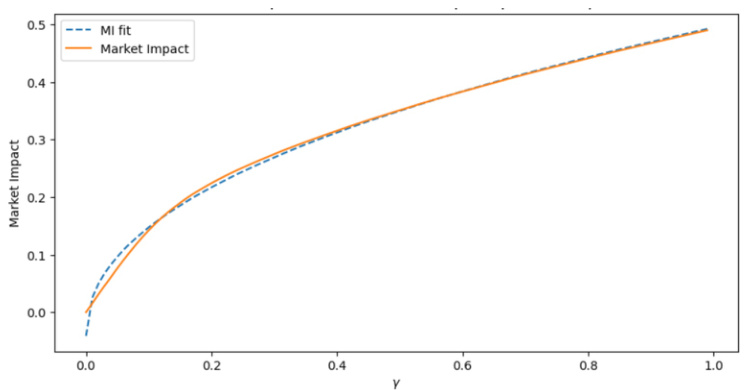
4.2 市场冲击一阶近似

• 为应对全模型推断数值复杂，采用线性近似：

\[
\kappa(x) \approx c\kappa x + d\kappa, \quad \lambda^L(x) - \lambda^C(x) \approx c\lambda x + d\lambda
\]

• 利用跳过程均值回复和泊松过程独立特性，推导订单簿差异\(\overline{q}s^{a,t} - qs^a \approx Us\)，满足如下随机差分动态：

\[
Us = Ut - \intt^s \int0^\infty \mathbf{1}{z \le - c\lambda U{u-}} \tilde{\pi}(du,dz)
\]

• 求期望动态解得：

\[
\mathbb{E}[Us|\mathcal{F}t] = Ut e^{c\lambda (s-t)}
\]

• 进一步推导市场冲击近似表达式：

\[
MIt \approx c\kappa \int0^t \mathbb{E}[Us dNs^a|\mathcal{F}t] + c\kappa \intt^\infty Ut e^{c\lambda (s-t)} \mathbb{E}[\lambdas^a|\mathcal{F}t] ds
\]

• 通过Hawkes过程条件强度公式展开\(\mathbb{E}[\lambdas^a|\mathcal{F}t]\)。
• 单笔限价单（即时冲击）示例：

- 只含单次跳点于\(t0\)，推导当\(t>t0\)时市场冲击估计

\[
MI{t0} \approx -\frac{c\kappa}{c\lambda} \frac{\mu}{1-\|\varphi\|{L^1}} + \text{噪声项}
\]

• 命题4.1：均值角度下，单位量限价单产生的即时冲击约为

\[
\pm \frac{c\kappa}{c\lambda} \frac{\mu}{1 - \|\varphi\|{L^1}}
\]

• 交易规模更大时（Metaorder）冲击表达式明确（命题4.2）：

\[
MIt = c\kappa \int0^t \int0^s e^{c\lambda (s-u)} f(u) du\, Ys^a ds + c\kappa \intt^\infty \int0^t e^{c\lambda (s-u)} f(u) du\, \mathbb{E}[Ys^a|\mathcal{F}t] ds
\]

• 该公式将执行策略强度\(f\)、限价单流动性响应参数、市场波动率\(Ys^a\)等市场可观测参数一体化，方便实际风险管理和交易策略评估。

4.3 Metaorder冲击评估应用

• 交易策略同时执行限价单强度\(f\)和市价单强度\(g\)。

- 市价单冲击参照[JR20]中的市场影响动力学近似表达，由函数\(\kappa^\)表示常规模糊冲击因子。

• 总冲击为限价单与市价单影响之和：

\[
MIt = MIt^l + MIt^m
\]

其中：

\[
MIt^l = c\kappa \int0^t \int0^s e^{c\lambda (s-u)} f(u) \sigmas ds + c\kappa \intt^\infty \int0^t e^{c\lambda (s-u)} f(u) \xit(s) ds
\]

\[
MIt^m = \kappa^ \int0^t (1 + \lambda^{-1} (t-s)^{-\alpha}) g(s) ds
\]

• 实证路径模拟（图2）展示限价单冲击轨迹，分为：

- \(t \le 1\) 时单调递增阶段，反映挂单量上升增强价格阻力；
- \(t > 1\) 时表现为波动阶段，冲击行为受随时间调整的市场波动率影响，平均水平维持稳定，体现冲击无弹性回撤现象。



---

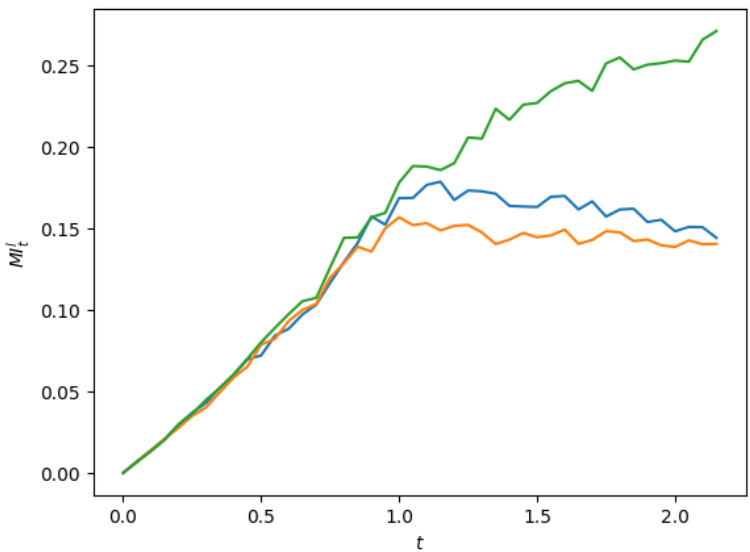
5. \(\kappa\) 函数校准（市场交易信息内容估计）

5.1 \(\kappa\)常数情形

• 经典[Jaisson 2015]模型，价格受控于市场订单流差异累积权重，价格单次跳动冲击为\(\pm \kappa \xi(0)\)，永久冲击为\(\kappa\)。

- 以现实市场价格半鞅模型为基础，采样频率\(\deltan\)下累积价格变差用以估计波动率，结合订单流总数估计\(\kappa\)：

\[
\hat{\kappa} = \sqrt{\frac{1}{\xi(0)^2 (NT^a + NT^b)} \sum{k=1}^{\lfloor T/\deltan \rfloor} (X{k \deltan} - X{(k-1)\deltan})^2}
\]

• 市场内很多订单为自激过程“内生性”交易，导致\(\|\varphi\|{L^1}\)接近1，即订单波动高度自相关。

- 可通过线性回归方法估计纯机械冲击强度\(\kappa\)和独立高频波动\(\tilde{\sigma}\)区分“主动-被动”影响。

5.2 \(\kappa\)与订单簿状态依赖

• 现实证据表明价格涨跌概率受到订单簿当前广义不均衡（差价挂单数量差异）的影响。

- 进阶模型中，令\(\kappa\)函数依赖于买卖限价单累积量\(q\)，简化形式：

\[
\kappa^2(q) = a + b q
\]

其中\(a,b\)为常数参数，可通过对波动计量值与成交价格变差的线性回归方法估计得出。

• 该模型明确反映高挂单量时信息传递效率降低，冲击减弱现象，为市场冲击测算提供更精细的量化依据[page::18–21]

---

图表解析

图1 市场影响幂律关系模拟

• 描述：图表展示了模拟得到的市场冲击随Metaorder参与率\(\gamma\)变化的曲线及其拟合幂律曲线（指数约0.54）。

- 解读：
- 曲线整体表现出与平方根规律相似的增长趋势。
- 支持了理论模型中限价单市场冲击表现为开区间幂函数的近似，体现流动性依赖及量化冲击强度间的非线性关系。

• 文本呼应：实验结果验证4.1节对市场冲击渐进形状分析的有效性，暗示模型能很好拟合实际大宗交易市场冲击特征[page::14]

图2 路径性市场冲击模拟（限价单）

• 描述：展示仿真情景下不同样本路径的时间序列市场冲击，参数为\(\alpha=0.6, \lambda=1, \gamma=0.5\)。

- 解读：
- \(t \leq 1\)阶段冲击呈上升、单调累积态，体现限价单挂单增加加大价格阻力。
- \(t > 1\)阶段冲击波动性增加且路径分化显著，符合该时间段冲击依赖未来波动情况下随机扰动增强的预期。

• 联系文本：与4.3节和4.2节中对路径市场冲击阶段性行为的理论预期一致，反映当Metaorder结束后市场冲击基本达到稳定，缺乏显著回弹[page::19]

---

估值分析

• 本文并非企业估值报告，而侧重市场冲击动态建模与预测，故无传统市盈率、市净率、DCF估值等内容。

- 估值思想集中在：
- 利用交易流强度及订单簿流动性函数建模价格的期望路径。
- 通过对冲击函数\(\kappa(\cdot)\)的功能形式推导，定量体现交易量与价格冲击态势。
- 队列反应函数\(\lambda^L, \lambda^C\)拟合订单簿流动性回复速度，影响冲击平稳态表现。

• 这为高频交易、算法执行成本评估及风险控制提供策略参数估计框架[page::4–17]

---

风险因素评估

• 模型风险：

- Hawkes过程及排队模型对真实市场订单动态的近似准确度存在不确定性，若模型参数估计错误，可能导致市场冲击预测失准。
- 模型假设市场订单流动性和价格变动之间存在特定函数关系，存在简化风险。

• 市场风险：

- 市场瞬时波动（\(Yt^a\)）强烈影响市场冲击，波动率异常高时，冲击预测可能出现较大偏差。

• 执行风险：

- Metaorder订单执行时限价单挂单可能不被触发，导致非执行风险影响价格冲击动态。

• 结构性风险：

- 订单簿状态耦合动态复杂，部分自然假设（如Poisson点过程独立）在实际交易中可能遭遇违背。

• 模型假设限制：

- 线性近似的环境下市场冲击表达更简洁，实际市场可能存在非线性和临界状态，复杂市场环境下模型可能失去解释力。

• 缓解策略：

- 通过实际数据标定\(\kappa, \lambda^L, \lambda^C\)，及时调整模型参数。
- 持续观测市场波动水平，动态校正Metaorder执行策略。

---

批判性视角与细微差别

• 报告对模型的数学严密性有充分证明，但实际应用时模型对订单簿状态的高度简化和Poisson点过程间独立性是假设中较强限制，可能导致偏差。

- \(\kappa(\cdot)\)函数形式的选取有一定灵活性，如何实证确定该函数形态的准确度是外部关键问题。

• 书中对市价单影响的总结依赖多个文献，而作者提出的被动限价单冲击模型新颖，但尚缺乏大量实证案例验证。

- 从结构上，模型不否认且部分体现市场机制对冲击的复杂非线性响应，但如限价单流动性的动态变化与交易者行为策略互动的更深层动态未被完全涵盖。

• 报告中多处“Elusive”性质（如限价单对市场冲击作用非直观，市场冲击无弹性回撤）提示该理论模型覆盖的市场机制仍需更丰富扩展。

- 文本中“停牌”“负积压”等非理想情形被允许存在，是理论模型灵活性的表现，但在实务中可能为异常事件，限制模型的普适度。

---

结论性综合

本文系统构建并分析了以Hawkes过程为框架，结合订单簿状态函数\(\kappa(q)\)的市场冲击动态微观结构模型。相比传统单纯以市价单为基础的冲击模型，本文深入探讨了限价单（被动流动性提供者）对价格形成和冲击传导的影响机制。

主要结论包括：

• 限价单挂单规模的增加实质上提升了市场流动性阻力系数\(\kappa\)的阻力，导致市场冲击呈现与挂单数量负相关的动态。

- 在大时间尺度下，该模型产生了基于市场订单流和限价订单簿变动的缩放极限，刻画了Metaorder执行中冲击的长期平均轨迹。

• 对冲击功能取线性近似后，推出了明确的量化公式，允许市场参与者根据可观测的限价单簿状态及交易强度，实时或事后评估策略的价格冲击成本。

- 数值模拟展示了冲击近似平方根增长特征，与经典市场经验规律高度吻合，突出了限价单流的非线性影响及动态机制。

• 校准方法通过关联成交价格波动和订单流计数，能够估计市场冲击中的信息传递强度参数\(\kappa\)，同时允许其依赖于订单簿的实时状态。

- 路径依赖性和市场冲击无明显回撤现象的发现，进一步丰富了我们对限价单流动性及市场影响的理解。

图表支持的深刻洞见：

• 图1模拟验证了市场冲击函数在参与率变化下遵循近似平方根幂律，实际市场冲击可接受幂函数模型近似，这一动态源于订单簿线性回复力和平滑流动性结构。

- 图2展示受限价单流影响下的路径性冲击演化，体现策略执行期内冲击单调积累，之后冲击稳定无明显回落，表明限价单流对价格的“抵抗力”特性。

综上，本文为深入理解和量化被动流动性对市场冲击的贡献提供了数学严谨且具有实用性的理论基础，为高级算法交易、交易成本分析和交易策略优化提供了价值工具与视角。该研究拓展现有市场冲击理论，填补了限价单市场冲击不足领域，但亦需未来研究融合更多实证数据验证与扩展市场行为复杂性。

---

参考溯源示例

• 市场冲击宏观定义与现象描述来自[page::1]

- 价格模型构建与数学表达式出自章节2.1与定理2.1[page::4–6]

• 缩放极限假设与过程收敛见章节3与定理3.6[page::8–13]

- 冲击渐进形式及幂律特征源自4.1节及图1[page::13–14]

• 一阶线性近似与路径市场冲击分析来自4.2、4.3节以及图2[page::15–19]

- \(\kappa\)函数校准方法与其市场意义见章节5[page::18–21]

报告