永续期权市场概述及模型设计 [page::0][page::1]

• 永续期权允许持有者无限期持仓，避免了传统期权频繁展期的高交易成本和流动性分散问题。

- 基于Black-Scholes模型，通过权重衰减的固定期限期权组合近似永续期权价格。

• 采用动态主动做市商（DPMM）根据库存调整标价，提高市场定价效率。

永续期权与固定期限期权滑点对比分析 [page::1]

• 永续期权滑点几乎保持不变，显示其流动性集中效果明显。

- 固定期限期权滑点呈抛物线形随库存变化显著增大，交易成本较高。

不同流动性水平下资金费用演变 [page::2]

• 高流动性池资金费用更低且波动减小。

- 更高行权价对应更大资金费用波动。

• 资金费用波动与流动性和行权价呈负相关和正相关关系。

流动性提供者(LP)收益与风险控制分析 [page::3][page::4]

• 结合DPMM与动态$\Delta$对冲策略的LP收益呈正态分布，平均收益正向且随着流动性增加趋势增强。

- DPMM模型表现稳健，夏普率达0.63，胜率90.8%，远优于传统AMM模型。

• 采用对冲策略显著缓释尾部风险，并提升整体盈利能力。

结论与未来展望 [page::4]

• 永续期权有效解决传统期权的流动性分散和交易成本高的问题。

- DPMM与动态对冲策略为LP提供了稳定且正向的收益路径。

• 提出未来研究将关注投资者行为及更优做市机制的探索。

对《Proactive Market Making and Liquidity Analysis for Everlasting Options in DeFi Ecosystems》研究报告的详尽分析

---

1. 元数据与概览

• 报告标题：Proactive Market Making and Liquidity Analysis for Everlasting Options in DeFi Ecosystems

- 作者及机构：Hardhik Mohanty, Giovanni Zaarour, Bhaskar Krishnamachari，均隶属于南加州大学维特比工程学院

• 发布日期：2025年8月12日

- 主题：去中心化金融（DeFi）生态内永续期权（Everlasting Options）的市场建模、流动性分析及主动做市机制

• 核心论点：

- 永续期权通过收取每日资金费用，解决了传统期权合约的滚动和流动性分散问题，提供了更高效的交易工具。
- 采用动态主动做市商（DPMM）模型分析其市场行为，揭示资金费用和交易成本在不同流动性条件下的表现。
- 流动性提供者（LP）可通过有效的Δ对冲策略实现净正收益，哪怕是在流动性低和交易成本高的环境中。
- 通过模拟和理论分析，强调永续期权对交易者和做市者的激励机制及其改善市场效率的潜力。

本报告旨在推进永续期权作为去中心化衍生品市场的替代品应用，并为流动性提供者的利润与风险管理提供实证依据。[page::0,1]

---

2. 逐节深度解读

2.1 摘要与引言（Abstract & Introduction）

• 要点总结：

- 永续期权允许持仓者通过支付每日资金费用永久持有头寸，避免了固定期限期权的频繁合约更换过程和由此产生的高昂交易成本与流动性分裂。
- 资金费依据期权市场价格与当日到期支付差额确定，将永续期权视为一组固定期限期权组合的加权递减和。
- 提供市场动态的分析框架，并提出了适合LP的Δ对冲策略，改善做市盈亏表现。

• 逻辑与假设：

- 使用Black-Scholes定价框架，假设永续期权的价格可等效于多个固定期限期权的组合，利用该数学工具简化复杂衍生品定价问题。
- 假设市场存在统一且充裕的流动性池，以支持永续期权的单一市场。
- 报告假设交易成本、流动性水平和市场波动均为核心影响因素。

• 重要数据点：

- 表1列出主流DeFi平台的期权流动性与做市机制差异，其中不同平台规模从数百万至数百亿美元不等，涵盖内部AMM、外部LP、订单簿模型等多种做市方式，为后续分析提供背景。[page::0]

2.2 相关工作综述（Related Work）

• 总结：

- 比特币永续合约的引入为加密货币衍生品市场奠定基础，期权作为重要衍生品，面临着传统DeFi期权的流动性碎片化与滚动成本问题。
- 永续期权由于其价格结构和资金费机制，更适合DeFi环境，特别是在动态主动做市商模型相结合时，能更高效地完成价格发现与风险管理。
- 现有研究集中于传统AMM与集中流动性，缺乏专门针对永续期权的流动性全面分析，填补了研究空白。

• 关键假设和术语：

- DPMM通过价格动态调整（与库存数量的平方成比例）实现对库存风险的管理，与常规AMM不同。
- 相关公式及符号定义详见表2，涵盖价格、波动率、流动性参数、对冲比例等，为后续模型和计算提供数学基础。[page::1]

2.3 方法论（Methodology）

• 3.1 GBM路径生成

- 假设基础资产价格遵循几何布朗运动（GBM），以每日为步长进行模拟，确保价格正值及收益对数正态分布。
- 公式为： \(S{t+\Delta t}=S{t}\exp((\mu - \frac{\sigma^2}{2})\Delta t+\sigma \sqrt{\Delta t} Z)\), 其中Z服从标准正态分布。

• 3.2 永续期权定价

- 通过对多个固定期限欧式看涨期权价格的加权递减和近似永续期权价格，展示永续期权的数学壳架。
- Black-Scholes典型定价公式用于计算固定期权价格，并以衰减因子D控制权重。

• 3.3 动态主动做市机制（DPMM）

- 价格标记根据当前库存规模进行调整，库存越大，价格偏离公平价值越显著以激励买卖平衡，公式为：
\[
Pm = i{\text{value}} \left(1 + k \left(\frac{V}{Q0}\right)^2 \right)
\]
其中，\(V\)为库存，\(Q0\)为参考流动性。

• 3.4 资金费用与交易成本

- 资金费用计算为标记价格减去即期支付，体现多空双方的资金转移。
- 交易成本模型涵盖了基础gas费和动态影响因子，并考虑市场波动与链上拥堵，具体公式复杂且包含随机变量的影响，反映实际链上交易成本波动。

• 3.5 LP的Delta对冲

- LP承担期权库存的市场风险，通过反向持有基础资产头寸进行风险中和，Delta按照期权希腊字母的基本定义计算。
- 通过每日调整仓位及库存限额，降低极端风险，保证风险与收益的平衡。

• 3.6 PnL计算

- LP的每日盈亏由三部分合成：对冲盈亏、资金费用收入和交易成本支出，即
\[
PnLt = PnLt^{hedge} + Ft - \mathcal{G}c
\]

• 模拟参数

- 模拟基于以太坊（ETH）价格，初始价$3000美元，年收益率3%，年波动率60%，覆盖180天，运行100次独立模拟以保证统计显著性。[page::1~3]

2.4 实验结果（Experimental Results）

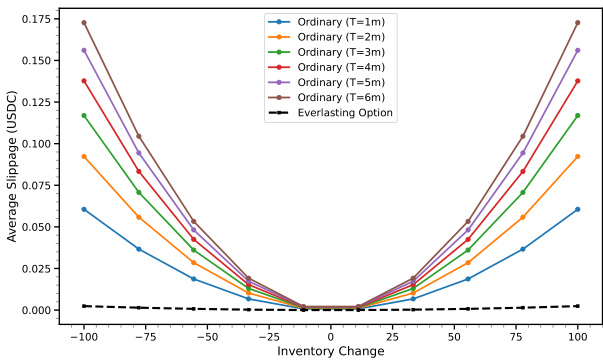
• 5.1 滑点分析（见图1）

- 永续期权的滑点对库存变化敏感度远低于固定期限期权，后者滑点呈抛物线趋势显著上升。
- 统一流动性池减少了交易时的价格冲击成本，特别适合大规模交易。

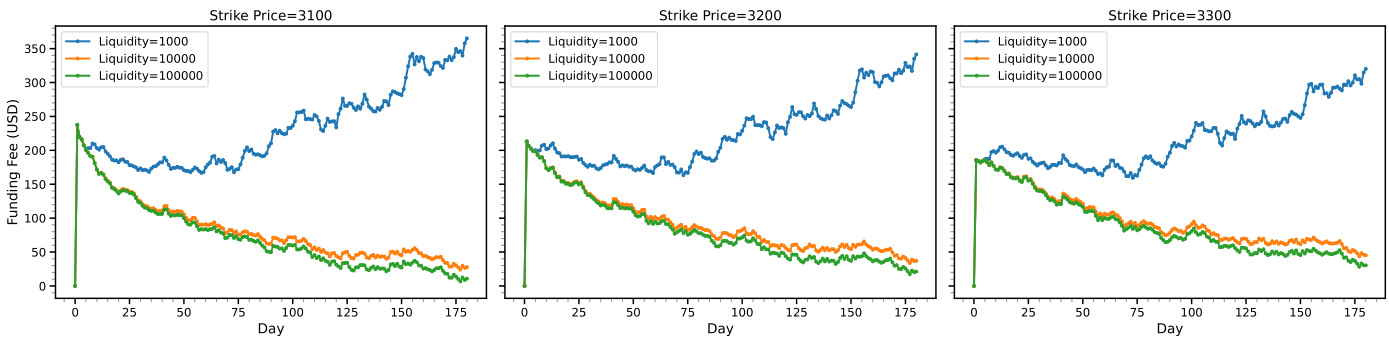
• 5.2 资金费用与交易成本（见图2）

- 资金费用随流动性增加而降低波动性，说明高流动性市场更稳定。
- 期权行权价越高，资金费用普遍偏大，反映风险-回报特性。
- 时间序列显示资金费用在初期有峰值，随后逐渐趋于平稳。

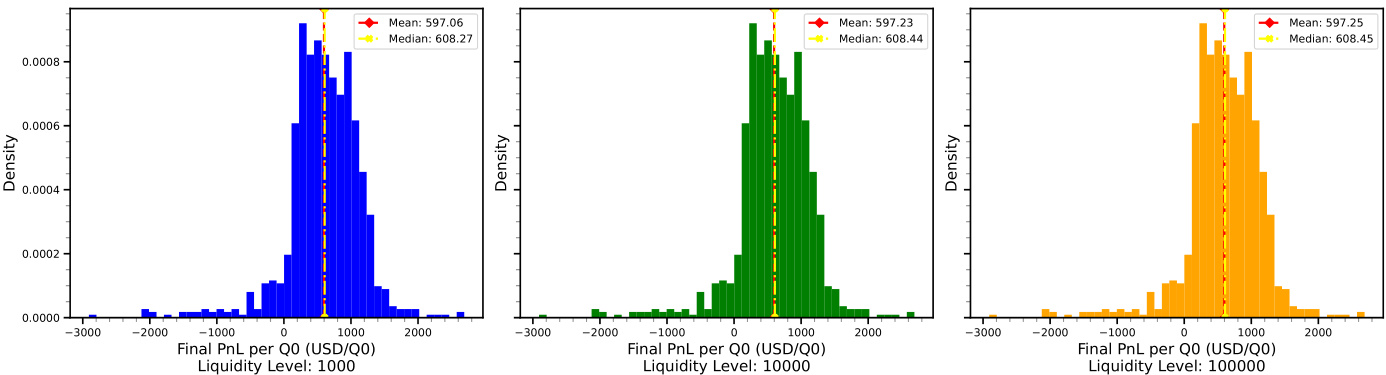
• 5.3 LP盈利能力分析（见图3）

- LP在不同流动性下的累积PnL分布均近似于正态分布，均值与中位数均为正，表明使用DPMM配合Delta对冲可实现稳健盈利。
- 流动性越高，LP平均收益越大，波动率适中，交易表现更优。
- 实际市场数据测试阶段，基于ETH价格和行权价为3200美元的永续看涨期权，LP实现正的220.74美元净收益，有效验证模型。

• 5.4 AMM 与 DPMM 比较

- DPMM模型因其库存敏感的动态定价和主动对冲策略，在收益波动率控制与盈利概率上表现更为稳定和优越（夏普率0.63，胜率90.8%）。
- 传统AMM虽然平均盈利能力较高，但中位数负值与极高波动暴露风险，夏普率较低且胜率不足一半，显示出较差的风险控制。
- 指出DPMM适合高波动及动态市场，AMM适合静态或待遇不频繁市场。

• 结论强调

- 永续期权通过单一流动性池降低流动性分散，提高交易效率。
- 资金费机制在合适流动性下保证市场稳定，减少价差波动。
- LP的Delta对冲策略有效控制风险，且盈利显著。
- 永续期权模型和市场机制为DeFi衍生品市场提供了强有力的替代方案，促进市场的健壮和可扩展增长 。[page::3,4]

---

3. 图表深度解读

图表1：滑点对比——永续期权 vs 固定期限期权

• 描述：该图呈现了不同库存变化下，永续期权与多期限固定期权的平均滑点（单位：USDC）。

- 解读：
- 永续期权的滑点几乎恒定且接近0，表现出极强的对冲流动性冲击的能力。
- 固定期限期权滑点随库存变动呈抛物线增长，尤其在库存极端变动时滑点高达0.175 USDC，表明多个独立池分散了流动性，导致较高交易摩擦。

• 联系文本：支持报告中永续期权通过资金费与单一池集中流动性降低交易成本的核心论点。

- 潜在局限性：图中仅为模拟数据，实际链上滑点可能受更复杂因素影响。

图表2：资金费用随流动性和行权价的变化趋势

• 描述：三个子图分别展示了行权价为3100、3200、3300 USD下，流动性规模为1000、10000、100000 USD时资金费用随时间（180日）的变化。

- 解读：
- 低流动性（1000 USD）的资金费波动最大且水平最高，表现出更大的资金费成本压力。
- 流动性增大到10万USD，资金费用快速收敛至较低且平稳水平，说明深度流动性可抑制资金费波动。
- 行权价升高，资金费用总体呈上升趋势，反映期权权利金与风险的增加。

• 联系文本：验证了资金费用稳定性和成本与流动性紧密相关，强调增加流动性的重要性。

图表3：不同流动性水平下LP最终PnL分布（归一化）

• 描述：三个直方图展示了流动性分别为1000，10000，100000 USD时，LP最终PnL归一化后的密度分布。红线和黄线分别表示均值和中值。

- 解读：
- 所有三级流动性PnL分布皆呈钟形且“右偏”，均数高于中位数，表明LP多头获利可能较集中。
- 增加流动性后，分布峰值更集中在更高正收益区域，显示盈利潜力显著提升。
- 流动性最低时尾部风险明显，两端具有概率较大负收益。

• 联系文本：支撑了DPMM配合Δ对冲策略能够实现稳健盈利的论断，也凸显流动性深度对LP风险收益的正面影响。

---

4. 估值分析

• 估值核心基于Black-Scholes期权定价模型，结合期权定价的连续时间金融数学。

- 永续期权的估值通过加权求和多个固定期限期权价格的递减序列来实现，权重由衰减因子D控制，确保无限期权近似有收敛性。

• DPMM中的价格调整机制基于库存的平方比例调节，体现风险弹性定价，这在定价过程中起到动态风险管理作用。

- 没有显式DCF或贴现债券估值，估值重点在于期权数学模型与市场动态之间的耦合。

---

5. 风险因素评估

报告中对风险明确提出包括：

• 流动性风险：低流动性会导致资金费高且波动性大，增加LP的成本与风险暴露。

- 市场风险：需要日常调整Delta对冲比例，目标控制风险暴露，库存上限避免极端亏损。

• 交易成本风险：链上交易气费波动和网络拥堵势必影响交易成本，使得对冲效率受限。

- 策略风险：Delta对冲假设波动率参数准确，且市场行为符合模型假设，偏离可能引发财务损失。

• 模型风险：Black-Scholes模型的假设（如波动率常数、正态收益分布）与加密市场现实存在差异，可能影响实际表现。

对这些风险，报告建议通过动态调整库存、流动性规模和对冲比例，以及设计合理的交易费用模型进行缓解。

---

6. 批判性视角与细微差别

• 报告优势：结构严谨，理论与模拟结合紧密，实验设计充分体现现实条件（如高波动率、链上交易成本）；首次系统研究永续期权流动性与市场效率。

- 潜在偏见：
- 模型基于Black-Scholes及GBM，典型假设可能低估加密市场跳跃风险与极端波动。
- 交易成本模型虽然涵盖拥堵因素，但链上不确定性可能更复杂。
- Δ对冲策略未探讨手续费大幅提升时的策略失效情况。

• 细微之处：AMM与DPMM性能对比显示AMM均值更高但中位数负值，证实AMM可能适合不同投资者偏好，但报告略缺对此现象深入的行为学分析。

- 数据局限：图表均基于模拟及有限实证案例，未涵盖多样市场环境及极端事件，后续需扩展验证。

---

7. 结论性综合

综上所述，本报告成功揭示了永续期权在DeFi生态系统中作为创新金融衍生品的巨大潜力：

• 永续期权显著优化了传统期权存在的流动性分散及高滚动成本问题，通过单一流动性池和资金费用机制，提升了交易效率与市场稳定性。

- 动态主动做市商（DPMM）结合库存敏感价格调整与Delta对冲策略，助力流动性提供者在复杂多变的市场环境下实现净正收益。

• 图1数据显示永续期权滑点低且稳定，远优于多期限固定期权池的滑点表现，为高频大额交易场景提供支持。

- 图2表明资金费用与流动性正相关，提升市场深度可降低资金成本波动，有利于各方稳定持仓成本。

• 图3证明LP通过DPMM与Delta对冲不仅能维持风险可控，还能实现长期盈利，流动性越强，盈利潜力越大。

- AMM与DPMM的比较强调了动态定价机制和主动风险管理的重要性，DPMM表现出更优的风险调整后收益和稳定性。

• 报告结尾提出未来研究方向包括从投资者角度深入分析永续期权交易行为，资金费用优化及新的做市策略设计，显示领域仍有丰富发展空间。

总体上，作者传达的主旨是：永续期权搭配DPMM是一种极具前景的DeFi衍生品市场机制，其有效性已获理论和模拟的多重支撑，具备助推DeFi衍生品市场成熟与增长的潜力。[page::0~4]

---

参考文献及致谢

报告引用了大量最新和经典文献，包括Black-Scholes定价基础、加密衍生品市场动态、DeFi流动性机制研究等，体现了扎实的研究基础与广泛的学术背景。

---

总结

本报告以数据、模型和模拟全面解析了永续期权在DeFi生态中的市场动态及风险/收益特征。其结合创新的主动做市商机制和风险对冲策略，为市场参与者提供了具备可操作性的策略和洞见，对推动去中心化衍生品市场的发展具有重要参考价值。视角独特且深入，适合金融工程、区块链及数字资产领域的专家学者和从业人员学习借鉴。

报告