Ultrasonic cavitation damage characteristics of materials and a prediction model of cavitation impact load based on size effect
创建于 更新于
摘要
本文基于球形压痕理论与Johnson–Cook本构并引入基于位错密度的尺寸效应,建立了含尺寸效应的空化冲击载荷、冲击压强与微射流速度预测模型,指出在微纳尺度凹坑形成过程中尺寸效应显著,考虑尺寸效应后预测值较传统模型可提高0.94%–322.5%,且对典型凹坑的反演结果(压力473–1131 MPa,速度355–848 m/s)更接近实验观测,从而验证了在空化反演分析中引入尺寸效应的必要性与合理性 [page::1][page::5].
速读内容
研究目的与方法 [page::2]
- 目标:解释为何高压高速微射流只在微纳尺度产生凹坑,并建立可逆算的空化冲击载荷与微射流参数预测模型。采用球形压痕等效理论、Johnson–Cook (J‑C) 本构并在其上叠加基于Taylor位错理论的尺寸效应修正项来描述微尺度塑性行为 [page::2].
- 方法要点:将凹坑几何(直径 dp、深度 hp)等效为球形压痕问题,求解等效应变、J‑C 应力 σJC,并通过GNDs(几何必要位错)引入尺寸效应系数得到修正应力 σp,再由投影面积算出冲击载荷、冲击压强与利用water‑hammer方程估算微射流速度 [page::3].
理论模型与尺寸效应 [page::3]

- 等效应变:εp ≈ 0.8·(hp / dp)(当 dp ≫ hp 时)[page::3].
- J‑C 本构用于描述高应变率下材料强度:σJC = (σ0 + B εp^{n1})(1 + C ln(ė/ė0)),忽略温度项用于本模型 [page::3].
- 尺寸效应修正:基于Taylor关系,引入GND密度ρ
- 冲击载荷与压强关系:Lp = ψ σp Ap(取完全塑性约束因子 ψ = 2.87,Ap = π dp^2/4),微射流冲击压强 σj = 4 Lp / (π dp^2) = 2.87 σ_p;速度由water‑hammer估算得到 [page::3].
主要结果与定量结论(含表/图) [page::4][page::5]

- 尺寸依赖:增大凹坑直径或增深均导致冲击载荷、压强与速度增加,但对直径的敏感性更强;在所选理论范围内,考虑尺寸效应后参数提升范围为 0.9408%–322.5%,在最小直径‑深度比(dp=2 μm, hp=2 μm)时增幅最大 [page::4].

- 极值示例(理论扩展区间2–15 μm、0.05–2 μm):带尺寸效应时冲击压强可达数百至上千 MPa(372.6–2478 MPa),速度可达数百至上千 m/s(279–1857 m/s);未考虑尺寸效应时范围显著偏小(≈369–605 MPa, 277–454 m/s)[page::4].
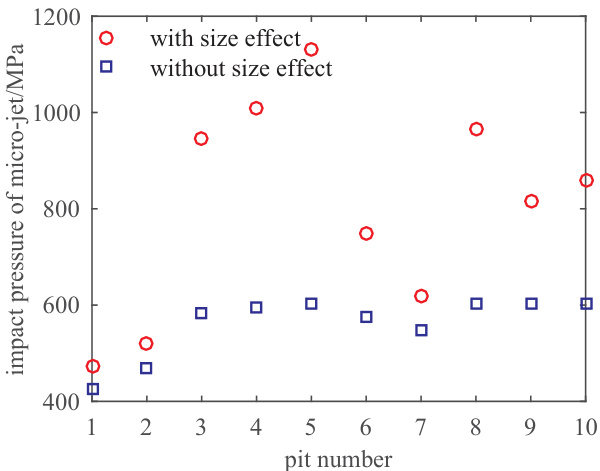
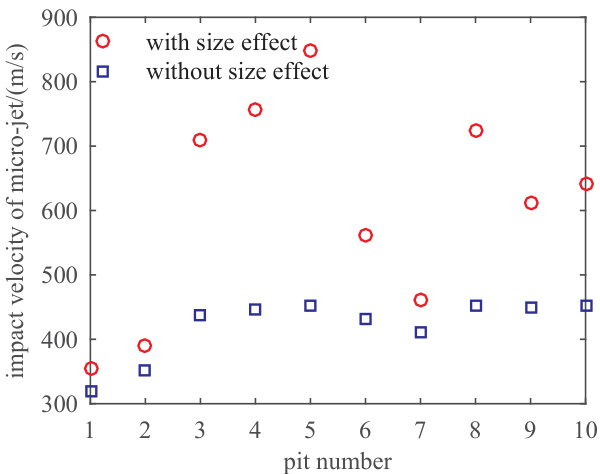
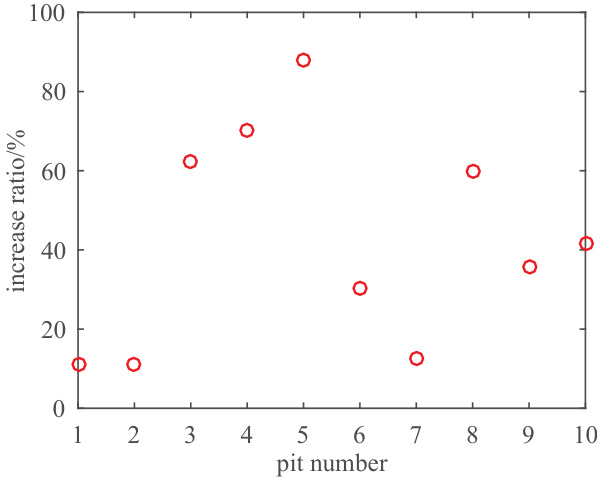
- 十个代表性凹坑反演(表格下)结果:带/不带尺寸效应的微射流压强与速度分别为 473–1131 MPa / 427–604 MPa 与 355–848 m/s / 320–453 m/s,平均增幅约 11%–88%,且带尺寸效应的速度与高速摄影观测更接近,支持尺寸效应修正的合理性 [page::5].
表 — Table 2: Sizes of ten representative pits [page::5]
| Pit number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|------------|------|------|-----|-----|-----|----|------|-----|------|------|
| Depth (μm) | 0.06 | 0.27 | 1.1 | 1.5 | 1.9 | 2 | 2.4 | 3.8 | 5.2 | 6.7 |
| Diameter (μm) | 4.07 | 7.76 | 4.8 | 5.1 | 4.9 | 10 | 18.6 | 8.8 | 14.1 | 14.5 |
- 基于上述十坑的反演图示(Fig.5–8)显示:带尺寸效应点值(红圈)系统高于不带尺寸效应值(蓝方),且相对增幅受dp与hp组合影响显著 [page::5].
工程或研究意义 [page::5]
- 在微纳尺度空化损伤反演与寿命评估中,忽略材料尺寸效应将低估冲击压强与速度,从而影响损伤机理推断与材料抗空化设计建议 [page::5].
深度阅读
报告元数据与概览
- 作者与单位:Linzheng Ye, Xijing Zhu, Yan He, Xumin Wei,来自 North University of China(山西先进制造技术重点实验室)与 Inner Mongolia Frist Machinery Group 等[page::1].
- 核心结论/作者意图:作者主张空化坑的等效应力、等效应变、微喷射冲击压力与速度在不考虑尺寸效应时只与坑的直径/深度比相关,但当考虑尺寸效应后,还将显著依赖坑直径本身;在所选尺寸范围内,考虑尺寸效应后预测值比不考虑时提高约0.94%–322.5%,并通过十个典型坑的反演说明考虑尺寸效应能使预测的微喷射速度更接近高速摄影观测值,从而验证方法的必要性与合理性[page::1][page::4][page::5].
逐节精读与剖析
1) 摘要与引言(研究动机与问题界定)
- 研究提出两点疑问:为何极端的高压/高速度塌陷仅在纳米/微米尺度上造成坑?以及如何有效反演/预测作用在材料表面的冲击压力与喷射速度[page::1].
2) 理论模型(材料本构与尺寸效应的引入)
- 选用 Johnson‑Cook(J‑C)本构模型处理高应变速率条件下的等效流动强度:σJC = (σ0 + B εp^{n1}) (1 + C ln(ėp/ė0))(忽略温度项),以体现应变硬化与应变率强化[page::3].
- 进而定义空化冲击载荷 Lp = ψ·σp·Ap(ψ 为约束因子,作者在完全塑性假设下取 ψ = 2.87;Ap ≈ π dp^2 /4)并导出带尺寸效应的 Lp 表达式以及微喷射的等效冲击压力 σj = 4 Lp / (π dp^2) = 2.87 σJC sqrt(1 + …);最后通过水锤方程将冲击压力转换为喷射速度 νj,完成链式预测模型[page::3].
关键数据点与模型参数(Table 1)
- 这些参数是模型数值预测的关键输入,尤其 σ0、B、n1、C 决定 σJC 的基线与应变/应变率响应,而 μ 与 b 决定尺寸项中 GND 引起的强化幅度[page::3].
图表与图像深度解读(每个图/表)
- 图 1(cavitation impact load under different pit sizes)呈三维曲面,横轴为坑直径 dp(2–15 μm)、纵轴为坑深 hp(0–2 μm),纵向高度为冲击载荷 Lp;图中标注“with size effect”和“without size effect”两表面,显示考虑尺寸效应后 Lp 整体提高且随 dp、hp 增大而增大,dp 对 Lp 的影响强于 hp,对应最大值约 0.1125 N(有尺寸效应)与 0.09719 N(无尺寸效应),增幅约 15.75%[page::3].
- 图像嵌入: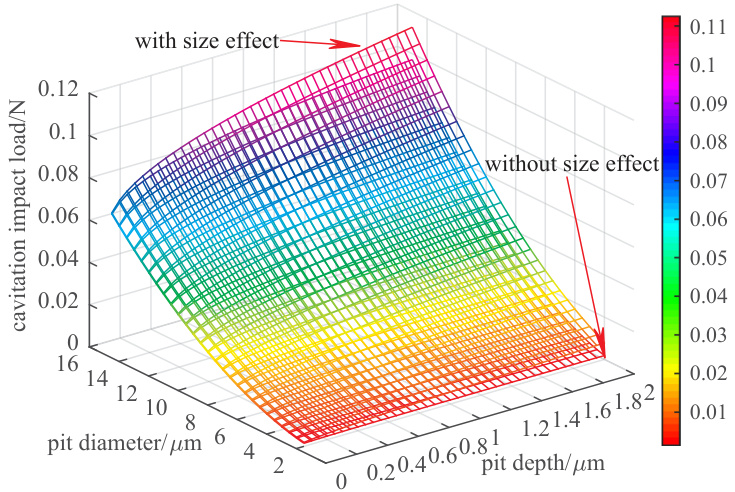 [page::3].
[page::3].
- 解释:Lp 与投影面积 Ap ~ dp^2 成正比,因此直径增加会显著提升载荷;尺寸效应系数对小尺度(小 dp)影响更大,使得在微小坑半径时强化效果更明显[page::3].
- 图像嵌入: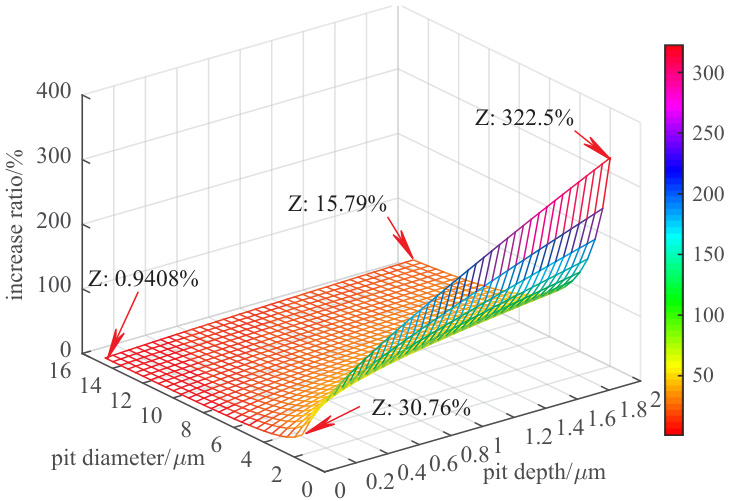 [page::3].
[page::3].
- 解释:这直接反映尺寸效应系数 ~ 1 + const·(hp/dp^2) 的数学结构,dp 在分母的平方项导致小直径时强烈增大。
- 图像嵌入: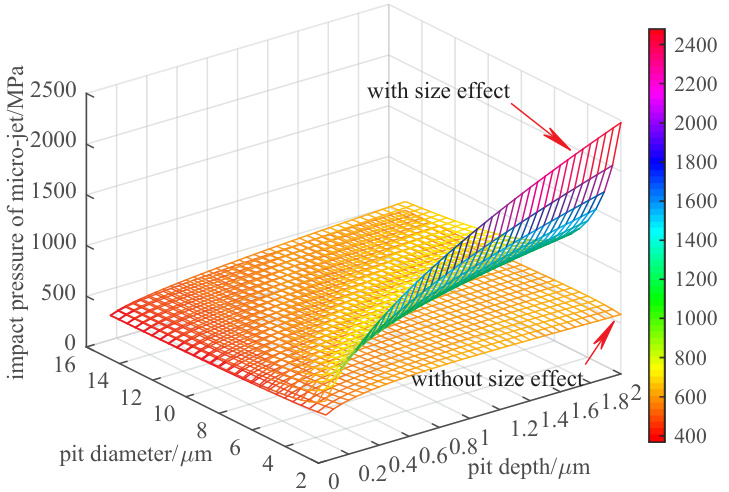 和
和 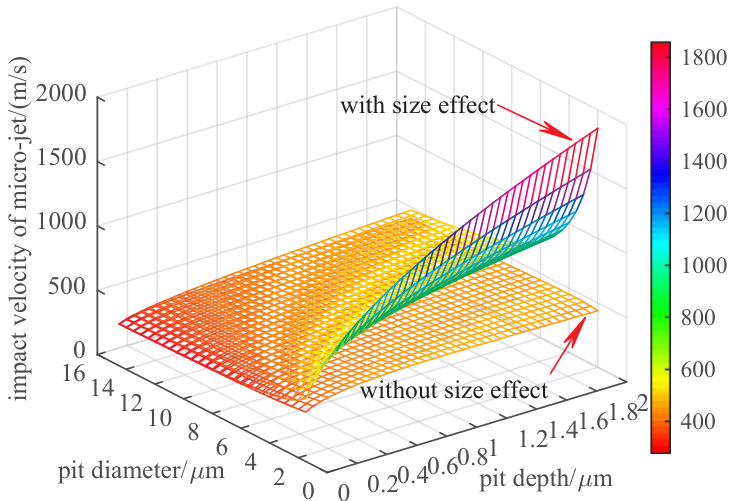 [page::3][page::4].
[page::3][page::4].
- 注:作者也强调这些极端理论值(如 dp=hp=2 μm 时的 ~2478 MPa、1857 m/s)在实践中不一定可达,仅用于揭示尺寸效应作用趋势[page::3].
- 表格嵌入说明:Table 2 来源于多篇文献整合而得,用于更实际的参数输入以避免理论极值偏离实际[page::5].
- 图像嵌入: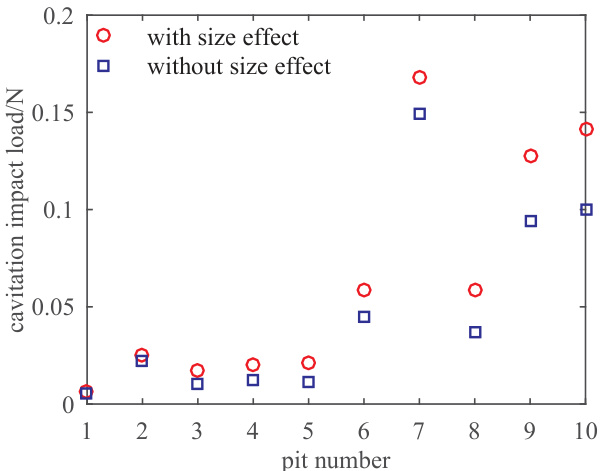 ,
, ,
, ,
, [page::4][page::5].
[page::4][page::5].
- 解释:这些反演结果更接近实验观测的速度区间(如文献报道的 ~200–700 m/s),从而支持作者认为引入尺寸效应能提高反演可信度[page::4][page::5].
估值分析(模型的灵敏度与“估值”类讨论)
- 建议(方法学上):应对 J‑C 参数(σ0、B、n1、C)以及 μ 与 b 的误差进行严格敏感性分析并给出不确定性带来的置信区间,当前论文主要给出点值和增幅范围,但未系统给出参数不确定性下的置信带,这在反演实际工件时是一个局限[page::3].
风险因素与局限性评估
- 几何近似与等效:将空化坑等同于球形压头的投影与等效应变是一种近似(在 dp ≫ hp 时采用简化 εp ≈0.8·hp/dp),对于形状复杂或非对称坑以及重叠坑情形可能偏差较大[page::3].
- 反演非唯一性:由表面几何反推微喷射压力/速度属于经典的逆问题,可能存在非唯一解—不同冲击历程(如压力时程形状、持续时间)可能产生相似坑几何,从而增加反演不确定性(论文未充分讨论逆问题的不适定性)[page::2][page::4].
批判性视角与细微差别
- 需慎重之处:1) 选择完全塑性的约束因子 ψ=2.87 的假设简化了弹塑过渡情形,实际坑可能处于弹塑混合区;2) J‑C 模型参数是否适用于非常短的纳秒尺度脉冲与极高应变率需要谨慎(虽然 J‑C 是常用模型,但其在极短时程下的适用性需通过实验验证)[page::3].
结论性综合(关键发现汇总)
- 主要定量结论:在所选的理论参数域(dp 2–15 μm,hp 0.05–2 μm)内,考虑尺寸效应将使预测的 Lp、σj、νj 增加约 0.9408%–322.5%,增幅随 dp 减小且 hp 增大而增加;在基于文献的十个代表性坑上,σj 从 427–604 MPa(无尺寸效应)增至 473–1131 MPa(有尺寸效应),νj 从 320–453 m/s 增至 355–848 m/s(有尺寸效应),约提高 11%–88%,且有尺寸效应的速度更接近高速成像的观测区间[page::3][page::4][page::5].
参考与附注
- 文中关键图像与表格引用如下以便核查:Table 1(参数)见图像嵌入 ;增幅三维图
;增幅三维图  ;十坑反演图见
;十坑反演图见  、
、 、
、 、
、 以供详细比对[page::3][page::4][page::5].
以供详细比对[page::3][page::4][page::5].
- 报告标题:Ultrasonic cavitation damage characteristics of materials and a prediction model of cavitation impact load based on size effect(超声空化对材料的损伤特征及基于尺寸效应的空化冲击载荷预测模型)[page::1].
- 作者与单位:Linzheng Ye, Xijing Zhu, Yan He, Xumin Wei,来自 North University of China(山西先进制造技术重点实验室)与 Inner Mongolia Frist Machinery Group 等[page::1].
- 主题与研究问题:以超声诱导近壁气泡塌陷产生的微喷射(micro‑jet)为出发点,研究形成材料表面“空化坑(cavitation pit)”的力学机制,重点在于把微纳尺度的“尺寸效应(size effect)”纳入材料本构与反演预测模型,从而建立含尺寸效应的冲击载荷、冲击压力与微喷射速度的预测模型并做反演分析[page::1][page::2].
- 核心结论/作者意图:作者主张空化坑的等效应力、等效应变、微喷射冲击压力与速度在不考虑尺寸效应时只与坑的直径/深度比相关,但当考虑尺寸效应后,还将显著依赖坑直径本身;在所选尺寸范围内,考虑尺寸效应后预测值比不考虑时提高约0.94%–322.5%,并通过十个典型坑的反演说明考虑尺寸效应能使预测的微喷射速度更接近高速摄影观测值,从而验证方法的必要性与合理性[page::1][page::4][page::5].
逐节精读与剖析
1) 摘要与引言(研究动机与问题界定)
- 作者指出微喷射和冲击波是造成材料空化损伤的两大机制,其中微喷射在近壁塌陷中占主导,留下典型的微纳尺度坑(直径典型为0.1–10 μm)并可能累积导致破坏[page::1].
- 研究提出两点疑问:为何极端的高压/高速度塌陷仅在纳米/微米尺度上造成坑?以及如何有效反演/预测作用在材料表面的冲击压力与喷射速度[page::1].
- 逻辑与出发点:作者认为关键在于微喷射作用时间很短且作用尺度微小,材料在微纳尺度的塑性表现会发生“尺寸效应(indentation size effect)”,因此需要把尺寸效应引入反演模型[page::2].
2) 理论模型(材料本构与尺寸效应的引入)
- 使用球形压入(spherical indentation)接触力学框架来类比空化坑的几何与等效应变,引用 Tabor 的接触边缘等效应变表达式并将坑深 hp 与坑直径 dp 代入,得出坑的等效应变 εp≈0.8·(hp/dp)(在 dp ≫ hp 的近似下)[page::3].
- 选用 Johnson‑Cook(J‑C)本构模型处理高应变速率条件下的等效流动强度:σJC = (σ0 + B εp^{n1}) (1 + C ln(ėp/ė0))(忽略温度项),以体现应变硬化与应变率强化[page::3].
- 为了刻画尺寸效应,作者基于 Taylor 位错理论与几何必要位错(GND)密度公式引入尺寸修正项,得到:σp = σJC · sqrt(1 + 54·hp·α^2·μ^2·b / (dp^2·σJC^2)),其中新增的乘子被称为“尺寸效应系数”(size effect coefficient),显示在有尺寸效应时等效应力不仅与 hp/dp 有关,而且与 dp 本身有关[page::3].
- 进而定义空化冲击载荷 Lp = ψ·σp·Ap(ψ 为约束因子,作者在完全塑性假设下取 ψ = 2.87;Ap ≈ π dp^2 /4)并导出带尺寸效应的 Lp 表达式以及微喷射的等效冲击压力 σj = 4 Lp / (π dp^2) = 2.87 σJC sqrt(1 + …);最后通过水锤方程将冲击压力转换为喷射速度 νj,完成链式预测模型[page::3].
关键数据点与模型参数(Table 1)
- Table 1 给出计算所用参数(Al1060 和水):液体密度 ρ0=1000 kg/m3,声速 c0=1480 m/s;固体(Al1060)密度 ρs=2707 kg/m3,声速 cs=5000 m/s;J‑C 参数 σ0=66.562 MPa,B=108.853 MPa,n1=0.23,C=0.029;α=0.5,μ=27 GPa,b=0.143 nm 等[page::3].
- 这些参数是模型数值预测的关键输入,尤其 σ0、B、n1、C 决定 σJC 的基线与应变/应变率响应,而 μ 与 b 决定尺寸项中 GND 引起的强化幅度[page::3].
图表与图像深度解读(每个图/表)
- 表格 Table 1(模型参数)说明:列出材料与流体的密度、声速与 J‑C 以及位错相关参数,直接用于代入模型计算[page::3]. 解读与潜在局限:参数来源为作者之前工作或文献引用,若这些参数在不同合金成分或热处理态下变化,预测结果敏感性可能显著,需在反演实际样品时使用测得或更接近的材料参数以减少误差[page::3].
- 图 1(cavitation impact load under different pit sizes)呈三维曲面,横轴为坑直径 dp(2–15 μm)、纵轴为坑深 hp(0–2 μm),纵向高度为冲击载荷 Lp;图中标注“with size effect”和“without size effect”两表面,显示考虑尺寸效应后 Lp 整体提高且随 dp、hp 增大而增大,dp 对 Lp 的影响强于 hp,对应最大值约 0.1125 N(有尺寸效应)与 0.09719 N(无尺寸效应),增幅约 15.75%[page::3].
- 图像嵌入:
 [page::3].
[page::3]. - 解释:Lp 与投影面积 Ap ~ dp^2 成正比,因此直径增加会显著提升载荷;尺寸效应系数对小尺度(小 dp)影响更大,使得在微小坑半径时强化效果更明显[page::3].
- 图 2(increase ratio of parameters with size effect)三维色带图显示随 dp 与 hp 变化的增幅百分比(0.94% 至 322.5%);最大增幅出现在 dp=2 μm、hp=2 μm(即小直径而较深时)[page::3].
- 图像嵌入:
 [page::3].
[page::3]. - 解释:这直接反映尺寸效应系数 ~ 1 + const·(hp/dp^2) 的数学结构,dp 在分母的平方项导致小直径时强烈增大。
- 图 3(impact pressure of micro-jet)与图 4(impact velocity of micro-jet)分别给出 σj 与 νj 在同一参数域下的三维曲面,均展示“with size effect”曲面明显高于“without size effect”曲面,数值区间分别扩大到约 372.6–2478 MPa(有尺寸效应)与 279.3–1857 m/s(速度)等极端值(理论范围)[page::3][page::4].
- 图像嵌入:
 和
和  [page::3][page::4].
[page::3][page::4]. - 注:作者也强调这些极端理论值(如 dp=hp=2 μm 时的 ~2478 MPa、1857 m/s)在实践中不一定可达,仅用于揭示尺寸效应作用趋势[page::3].
- 表 2(十个代表性坑的尺寸)列出十个坑的 hp 与 dp(例如坑1:hp=0.06 μm,dp=4.07 μm;坑6:hp=2 μm,dp=10 μm 等)用于实际反演[page::5].
- 表格嵌入说明:Table 2 来源于多篇文献整合而得,用于更实际的参数输入以避免理论极值偏离实际[page::5].
- 图 5–8:对这十个坑分别绘制了 Lp、σj、νj 与增幅百分比的点图,结果显示有/无尺寸效应下的 σj 分别约 427–604 MPa(无)与 473–1131 MPa(有),νj 分别约 320–453 m/s(无)与 355–848 m/s(有),总体增幅约 11%–88%,并且有尺寸效应下的速度更接近高速摄影观测[page::4][page::5].
- 图像嵌入:
 ,
, ,
, ,
, [page::4][page::5].
[page::4][page::5]. - 解释:这些反演结果更接近实验观测的速度区间(如文献报道的 ~200–700 m/s),从而支持作者认为引入尺寸效应能提高反演可信度[page::4][page::5].
估值分析(模型的灵敏度与“估值”类讨论)
- 本文并无金融/价值评估意义上的估值分析部分,因此“估值分析”在财务语境下不适用;但在工程预测语境下应进行敏感性/不确定性分析,作者在文中用 dp、hp 的参数扫掠与典型坑反演完成了某种形式的敏感性研究,并指出尺寸效应主要通过项 ~hp/dp^2 影响最终结果[page::3][page::4].
- 建议(方法学上):应对 J‑C 参数(σ0、B、n1、C)以及 μ 与 b 的误差进行严格敏感性分析并给出不确定性带来的置信区间,当前论文主要给出点值和增幅范围,但未系统给出参数不确定性下的置信带,这在反演实际工件时是一个局限[page::3].
风险因素与局限性评估
- 参数依赖与普适性:模型对材料本构参数(J‑C)与微观参数(μ、b)高度敏感,若实际样品的化学成分、晶粒度或表面状态不同,预测误差可能显著[page::3].
- 几何近似与等效:将空化坑等同于球形压头的投影与等效应变是一种近似(在 dp ≫ hp 时采用简化 εp ≈0.8·hp/dp),对于形状复杂或非对称坑以及重叠坑情形可能偏差较大[page::3].
- 动力学与时效假设:作者假设塑性变形主要发生在高峰压力阶段(持续仅几纳秒),并据此采用 J‑C 模型忽略温度项;但若实际过程伴有显著热软化或多次冲击累积,忽略温度和循环效应会影响准确性[page::3].
- 反演非唯一性:由表面几何反推微喷射压力/速度属于经典的逆问题,可能存在非唯一解—不同冲击历程(如压力时程形状、持续时间)可能产生相似坑几何,从而增加反演不确定性(论文未充分讨论逆问题的不适定性)[page::2][page::4].
- 实验验证范围:作者以文献中十个坑进行反演并与高速摄影速度区间对比,说明合理性,但仍需更多针对同一坑同时测得冲击过程(例如同步高速成像与局部应变/温度测量)的实测数据来进一步验证模型[page::4][page::5].
批判性视角与细微差别
- 优点:作者将微纳尺度的尺寸效应系统地引入空化坑反演中,并从解析层面给出尺寸项的形式(依赖 hp/dp^2),清晰地揭示了为何小直径深坑会产生相对更大的强化效果,这在以往多用宏观本构的反演研究中相对缺失[page::3][page::4].
- 需慎重之处:1) 选择完全塑性的约束因子 ψ=2.87 的假设简化了弹塑过渡情形,实际坑可能处于弹塑混合区;2) J‑C 模型参数是否适用于非常短的纳秒尺度脉冲与极高应变率需要谨慎(虽然 J‑C 是常用模型,但其在极短时程下的适用性需通过实验验证)[page::3].
- 建议改进:给出参数敏感性(如表格或热图展示 σj、νj 对 σ0、μ、b 的敏感度),以及对反演非唯一性和参数估计的不确定度进行量化(例如蒙特卡洛或贝叶斯反演)将大幅增强结论的稳健性[page::3][page::4].
结论性综合(关键发现汇总)
- 方法与贡献:本文构建了一个将球形压痕理论、J‑C 高应变率本构与 Taylor 位错/几何必要位错机制结合的混合解析模型,从而在空化坑反演中引入了尺寸效应系数并给出闭式表达,形成从坑几何(dp、hp)到冲击载荷 Lp、冲击压力 σj 与微喷射速度 νj 的完整链式预测关系[page::3].
- 主要定量结论:在所选的理论参数域(dp 2–15 μm,hp 0.05–2 μm)内,考虑尺寸效应将使预测的 Lp、σj、νj 增加约 0.9408%–322.5%,增幅随 dp 减小且 hp 增大而增加;在基于文献的十个代表性坑上,σj 从 427–604 MPa(无尺寸效应)增至 473–1131 MPa(有尺寸效应),νj 从 320–453 m/s 增至 355–848 m/s(有尺寸效应),约提高 11%–88%,且有尺寸效应的速度更接近高速成像的观测区间[page::3][page::4][page::5].
- 实践意义:作者论证了在微纳尺度空化损伤反演中纳入尺寸效应的必要性与合理性,为更可靠地从表面坑形反推出微喷射冲击参数提供了理论工具,但在应用到具体工件或不同材料体系时需进行相应的参数校准与不确定性评估[page::3][page::5].
参考与附注
- 文中关键图像与表格引用如下以便核查:Table 1(参数)见图像嵌入
 ;增幅三维图
;增幅三维图  ;十坑反演图见
;十坑反演图见  、
、 、
、 、
、 以供详细比对[page::3][page::4][page::5].
以供详细比对[page::3][page::4][page::5].




