• 核心概念定义 [page::0][page::1]：

- 提出了“货币化套利利润”，即套利获得净代币数乘以该代币在中心化交易所（CEX）价格。
- 传统套利只针对单一代币（例如Ether），忽略了代币在CEX价格差异，可能导致非最优收益。

• 三种套利策略比较 [page::1][page::4]：

- MaxPrice策略：从价格最高的代币开始套利，但该策略并不总能获得最大货币化利润。
- MaxMax策略：轮流计算每种代币作为输入时的货币化利润，选择最大者，理论上优于MaxPrice策略。
- 凸优化策略：将MaxMax策略转化为凸优化问题，理论上利润最高，实证中与MaxMax策略收益几乎相同。

• AMM套利利润优化数学模型及求解 [page::2][page::3]：

- 利用Uniswap V2的常数乘积模型，定义输入输出代币数量与储备关系函数，构造利润最大化单变量凸函数。
- 利润最大点满足导数等于1，可用二分法数值求解，保证凸性与单峰特性。

• 策略举例演示 [page::4][page::5]：

- 以三代币套利环路为例，设置流动性池储备和CEX价格，分别计算不同策略利润。
- 结果显示MaxMax策略利润显著高于仅单一路径策略，凸优化策略优于MaxMax策略。

- 凸优化策略回测收益随起始代币价格变化优于MaxMax策略表现。

• 实证数据验证 [page::5][page::6]：

- 基于2023年9月1日Uniswap V2链上数据构造代币交易图，筛选超过阈值流动性池，检测123个三代币套利环路。
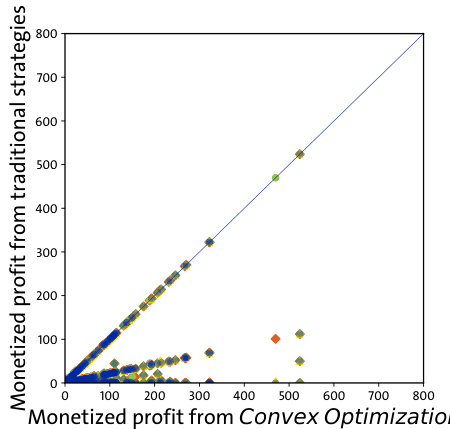
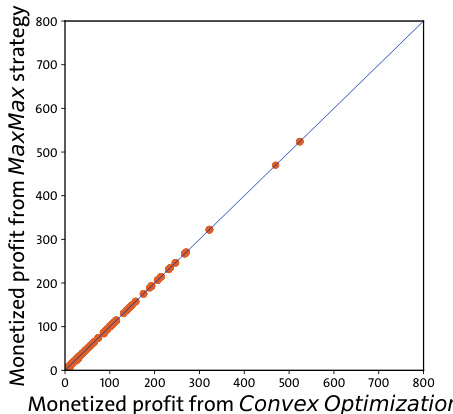
- 实证对比传统策略、MaxPrice、MaxMax及凸优化策略利润，确认MaxMax策略为传统策略上界，凸优化策略略优于MaxMax策略但差异有限。

• 策略适用性与计算复杂度分析 [page::6]：

- MaxMax策略需对每个代币计算一次，计算快速，适合较长环路。
- 凸优化策略计算量较大，尤其环路较长时耗时达秒级，可能不适用于极短区块环境。

• 投资及研究启示 [page::6][page::7]：

- 传统仅针对单一代币的套利计算可能严重低估套利利润。
- MaxMax和凸优化策略为套利程序设计提供更精确、收益更优的算法框架。
- 未来研究可探讨这两种策略间理论上的差异及更复杂多代币套利优化模型。

报告详尽分析报告

---

1. 元数据与概览

• 报告标题：Profit Maximization In Arbitrage Loops

- 作者：Yu Zhang、Zichen Li、Tao Yan、Qianyu Liu、Nicolo Vallarano、Claudio J. Tessone

• 机构：苏黎世大学、香港中文大学

- 日期：未明确标出，文中引用的最新数据为2023年9月，可推测为2023年底或2024年初发表

• 研究主题：去中心化交易所（DEXs）特别是Uniswap V2上的套利机会与套利利润最大化策略研究

- 核心论点：传统套利策略仅以某一特定Token（如Ether）输入出发，忽视了在中心化交易所（CEXs）不同Token价格的差异，进而无法获得最大化的“货币化（monetized）”套利利润。报告提出并系统对比了三种套利利润最大化策略（MaxPrice策略、MaxMax策略和凸优化策略），其中凸优化策略能够理论上获得最高的货币化套利利润。最终通过例子和实证数据验证了三种策略的效果差异，指出MaxMax和凸优化策略在实践中的高度接近性以及传统策略和MaxPrice策略的不可靠。[page::0,1,2,3,4,5,6]

---

2. 逐节深度解读

2.1 摘要部分与引言（第一页）

• 关键论点：

- 在Uniswap V2这类基于AMM（自动化做市商）模型的DEX中，存在大量循环套利机会。
- 传统套利利润计算仅针对某一特定Token输入输出，忽视CEX上价格差异。
- 定义“货币化套利利润”为：套利中获得Token净数量乘以该Token在CEX中的价格。
- 提出了三种策略：MaxPrice（从CEX价格最高Token入手），MaxMax（依次计算每个Token输入的货币化套利利润，并取最大值）和凸优化策略（将MaxMax策略映射为凸优化问题，理论上获利更高）。
- 实证表明，MaxPrice策略表现不稳定，凸优化策略和MaxMax策略在实际中利润相近。

• 背景介绍：

- DeFi与DEX的重要性与当前市场规模。
- Uniswap作为最大DEX采用恒定乘积AMM，导致价格滑点限制套利利润。
- 以币对储备比率定义即时价格，套利存在于价格乘积大于1的循环。
- 文献回顾表明大量研究聚焦于基于单一Token套利路径，而本研究强调多Token、价格多层面的利润最大化视角。[page::0,1]

2.2 相关工作（第二页上半）

• 论点：

- 报告归纳已有文献多聚焦于套利路径识别（通过三角套利检测、Bellman-Ford、Johnson算法等），但缺乏对“货币化套利利润”最大化系统研究。
- 特别引用Danos等人的凸优化思路，但指出其套利路径复杂难以实际操作，启发本文将凸优化用于利润最大化而非路径发现。

• 创新点强调：

- 本文主攻“最大化货币化套利利润”策略，与前人仅关注套利检测和单Token利润计算区分明显。[page::1]

2.3 AMM交换规则与MaxMax策略（第二页下半至第三页中）

• 核心内容：

- 明确Uniswap V2采用恒定乘积市场做市商模型（CPMM），定义公式：\[ (x + (1-\lambda)\Delta x)(y - \Delta y) = xy = k \]，其中λ为手续费率，Δx输入量，Δy输出量。
- 定义了两个Token价格单元之间的价格关系通过储备比计算。
- 价格乘积超过1的Token循环即为套利机会。
- 详细推导套利利润的最大化数学模型，利润为输入Token净多出量：\(\max(\Delta x{out} - \Delta x{in})\) ，其中输出量通过逐池函数嵌套递归计算，函数单调递增且凸。
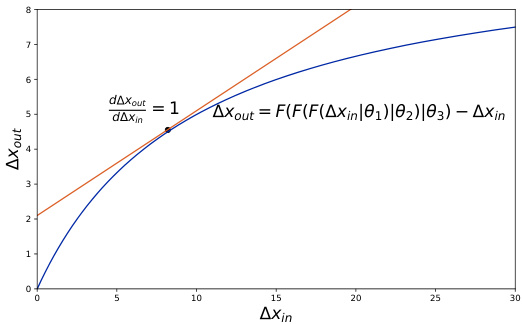
- 证明了最优输入量即为导数等于1时的输入量（边际输入等于边际输出），并展示了用二分法求解的可行性（图1）。
- 说明在输入一个Token后，循环中其它Token的参数也会相应调整，且套利余地会缩小。

• 核心数据点与公式：

- 输入输出的函数关系\(F(\Delta x | \theta)\)单调增且凸性是算法实现的数学基础。
- 三Token循环具体模型中输入量、价格及手续费率参数的结合。

• 重要观点：

- 该函数的凸性和单调性便于寻找最优输入量，确保利润最大化问题可用优化手段解决。
- 最大利润的临界点为导数1处，超出则边际利润递减。

• 图1：展示利润函数曲线和斜率为1的切线交点，直观说明最优输入点。[page::2]

2.4 货币化套利利润及三个策略表达（第三页下半）

• 扩展利润定义

- 利用CEX价格，定义货币化套利利润为Token净利润乘以CEX价格，如 \(Px (\Delta x{out} - \Delta x{in})\) 。
- MaxMax策略表达为对所有Token输入计算货币化套利利润后选最大值，数学表达为：
\[
\max \{ \max[Px(\Delta x{out} - \Delta x{in})], \max[Py(\Delta y{out} - \Delta y{in})], \max[Pz(\Delta z{out} - \Delta z{in})] \}
\]

• 说明：MaxMax策略确保利润不会低于任何单一Token起点策略。

- 引入Convex Optimization策略：
- 将MaxMax策略转换为凸优化问题，目标函数为三种Token净利润货币化和，附带池储备约束和内在的AMM不变乘积约束，优化变量为各输入输出数量。
- 表达的形式保证该优化具有唯一解且为凸问题，便于计算最优解。
- 该方法理论利润大于或等于MaxMax策略。

• 安全性约束说明：

- 介绍约束条件（如输出不小于输入量）保证套利是无风险的；若约束放宽则可能涉及借贷或做空，风险升高，故不讨论。

• 延拓性：方法同样适用于任意长度循环，非仅三Token。

- 无套利情况证明：若传统策略检测无套利机会，凸优化策略亦无法创造套利。[page::3,4]

2.5 案例比较（第四页）

• 假设与参数：

- 三种Token循环：储备(x,y)=(100,200)，(y,z)=(300,200)，(z,x)=(200,400)。
- DEX价格比率：Px/Py=2，Py/Pz=2/3，Pz/Px=2，乘积大于1，存在套利机会。
- CEX价格分别为\( Px=2, Py=10.2, Pz=20 \)美元。

• 关键结论：

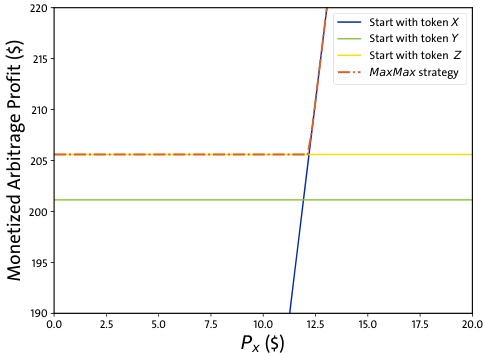
- 传统仅从Token X起点套利利润仅33.7美元，相较于Y起点201.1美元、Z起点205.6美元明显偏低。
- MaxMax策略为三路径利润最大值，防止选错起始Token导致利润流失。
- MaxPrice策略（单看最高价Token Z）并非总能获得最优利润（图2中黄色线与蓝线差异）。
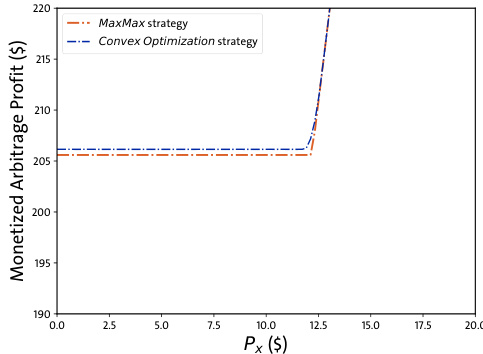
- 凸优化策略可进一步提高利润至206.1美元，高于MaxMax策略，且操作路径可灵活调整，建议结合闪电贷实现无风险套利执行。
- 凸优化策略需要更多总输入量，但利润更高。

• 图2：展示随着Token X CEX价格变化，三种起点套利路径及MaxMax利润变化关系，体现MaxMax策略的优势及MaxPrice策略的不稳定。[page::4]

2.6 凸优化与MaxMax实证对比（第五页至第六页）

• 图3：展示随着Token X价格变化，凸优化策略始终获得不低于MaxMax的利润，证明理论推导的实证符合。

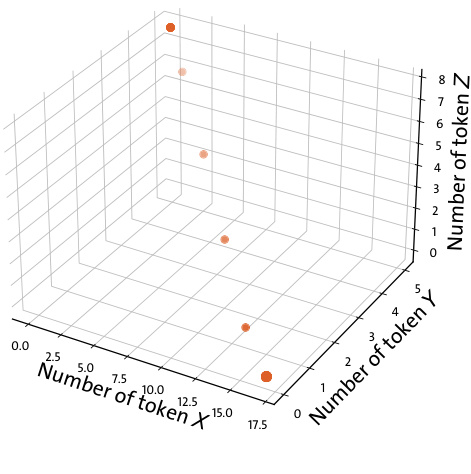
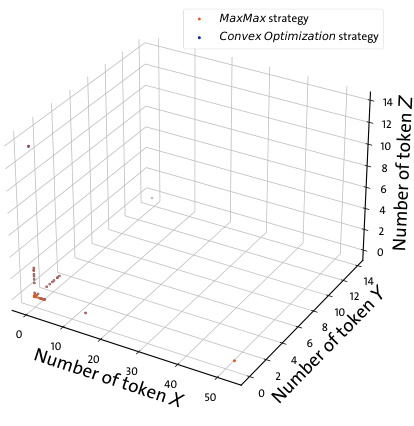
- 图4：3D散点图展示Token X, Y, Z的套利净利润数量分布，不同最优点分布显示套利变化非线性复杂，表明解析解较难。

• 实证数据分析：

- 构建了2023年9月Uniswap V2池子数据，挑选TVL大于3万美元且Token储备超过100的池子，构建51个Token和208条边的图。
- 找出123个3-token长度的套利循环。
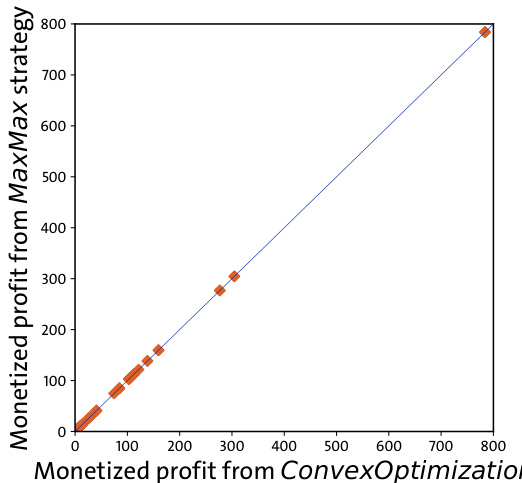
- 通过比较MaxMax策略与传统策略散点图（图5），MaxMax始终处于或偏上，证明MaxMax总是优于单一路径选择。
- 比较MaxPrice策略（图6），发现其常常低于MaxMax，验证其不可靠性。
- 凸优化与MaxMax利润散点几乎重合（图7），说明两者在实证层面差别极小，但凸优化计算复杂度较大。
- 按Token数量净利润维度对比（图8），两策略结果重叠。

• 效率与实践权衡：

- MaxMax需对n个Token分别计算，计算简单快速（毫秒级），适合实战。
- 凸优化计算更复杂（秒级），可能妨碍基于区块时间的交易时效。

• 其他说明：无套利情况下，凸优化与MaxMax策略一致无收益，从代码和优化约束得到验证。[page::5,6,7]

2.7 结论与未来展望（第六页）

• 研究贡献总结：

- 首次系统提出并验证货币化套利利润最大化理论，引入“MaxMax策略”和“凸优化策略”两个新方案。
- 理论与实证均证明MaxMax优于传统及MaxPrice策略。
- 凸优化策略理论获利最高，实证接近MaxMax策略，但计算时间较长，限制实际应用。
- MaxPrice策略不适于大规模套利利润最大化，容易产生获利低估。

• 实操建议：

- MaxMax策略因计算速度快，更适合集成于DeFi套利机器人。
- 凸优化策略适合学术或离线分析。

• 未来研究方向：

- 理论上量化凸优化与MaxMax策略利润差异。
- 扩展更长循环且考虑资金成本和风险的实际套利策略设计。

• 附录：四Token循环实证结果与三Token类似，验证方法的通用性。[page::6,7]

---

3. 图表深度解读

图1（page 2）

• 说明：展示三Token循环中，以Token X作为输入，输出数量与输入数量曲线（蓝色），及其斜率为1的切线（橙色）。

- 解读：
- 利润最大时输入输出差值最大，对应导数等于1点。
- 二分法可高效定位此点，从而找到最优投入量。

• 关联文本：支持数学推导效率和利润最大化理论基础。[page::2]

图2（page 4）

• 说明：以Token X CEX价格为横轴，纵轴为货币化套利利润，四条曲线分别是以X、Y、Z单Token起点路径，以及MaxMax策略。

- 解读：
- MaxMax曲线（红点虚线）始终为上界。
- MaxPrice（以价格最高Token Z起点，黄色线）不稳定，有时显著低于MaxMax和其它路径。
- 显示当Token X价格接近某值时，从X起点路径的利润大幅上升超越MaxPrice，验证单纯看价格选Token入手并非最优。

• 关联文本：实证反驳MaxPrice 策略有效性，强调MaxMax策略合理性。[page::4]

图3（page 5）

• 说明：以Token X价格为横轴，纵轴是Convex Optimization策略与MaxMax策略的利润对比。

- 解读：
- 两曲线高度重合，凸优化策略利润恒大于或等于MaxMax，实证体现理论预期。

• 关联文本：凸优化策略优势的现实体现，尽管理论最优利润与MaxMax差异微乎其微。[page::5]

图4（page 5）

• 说明：三维散点图显示Token X、Y、Z净利润数量分布，点大小代表整体利润大小。

- 解读：
- 净利润最优点集中于有限几个区域，利润与Token价格非线性关系复杂。

• 关联文本：揭示套利利润计算非线性特色，凸显解析难度。[page::5]

图5（page 6）

• 说明：散点图比较MaxMax策略与传统策略的货币化套利利润。

- 解读：
- 所有点均在或靠近45度线下方，说明传统策略套利利润不超越MaxMax，印证MaxMax为传统策略上界。

• 关联文本：实证支持MaxMax策略优越性。[page::6]

图6（page 6）

• 说明：比较MaxMax策略与MaxPrice策略利润。

- 解读：
- 多数点集中于45度线下方，显示MaxPrice策略多数情况下低于MaxMax，验证其不可靠。

• 关联文本：进一步否定以价格最高Token入手的简化策略。[page::6]

图7（page 6）

• 说明：散点图比较Convex Optimization策略与MaxMax策略。

- 解读：
- 点均分布在45度线附近，利润极度接近，凸优化策略虽理论更优但实际提升甚微。

• 关联文本：实证说明两者几乎无差异，凸显MaxMax作为实用策略的合理性。[page::6]

图8（page 7）

• 说明：三维散点图展示两种策略下，三Token净利润数量分布点的重合。

- 解读：
- 两种策略的结果点重合，表明在Token收益构成上亦无显著差异。

• 关联文本：强化利润不仅货币化值相近，具体Token分布结构也趋同。[page::7]

图9、图10（附录，第7页）

• 说明：四Token循环的各策略利润比较，图形结构与三Token循环类似。

- 解读：
- 凸优化策略对比传统策略展示显著优势。
- 凸优化和MaxMax策略利润高度一致。

• 关联文本：验证三Token研究结论的推广性。[page::7]

---

4. 估值分析

• 本报告不属于典型金融公司估值，而是针对DeFi交易路径套利利润问题的数学建模与算法效率估计。

- 三种套利策略即为不同优化模型：
- MaxPrice策略：单节点启始，无优化。
- MaxMax策略：多节点轮询优化单变量凸函数。
- 凸优化策略：多变量凸优化问题，为理论最优。

• 关键输入参数：

- 各流动池Token储备量（x,y,z等）。
- 交易手续费率λ。
- CEX上Token价格\( Px, Py, Pz \)。

• 优化指标为净套利Token数量乘以对应价格之和的最大化。

- 方法基于AMM不变积机制凸函数特性，与股票/企业估值不同，但体现了DeFi套利算法领域的“估值”问题。

---

5. 风险因素评估

• 报告未深入讨论市场风险、交易费波动、执行风险或价格冲击。

- 只对约束条件涉及的“无风险套利”定义做限定，强调只有满足输出不小于输入才能保证无风险。

• 凸优化去除这约束可导致借贷或做空行为，风险升高，故不在研究范围。

- 实际操作风险（交易延迟、链上拥堵、闪电贷失败等）未涉及，属于理论模型局限。

• 需用户自行结合实际区块链环境进行风险控制。

---

6. 批判性视角与细微差别

• 虽然凸优化策略理论优于MaxMax策略，但实证中两者利润差异极小，计算复杂度大幅增加，凸显技术与实践间的权衡。

- MaxPrice策略虽便利，实际盈利不可控，易产生误判。报告无过度美化且开放讨论其缺点，体现严谨态度。

• 报告对“套利循环检测”问题刻意忽略，聚焦利润最大化，体现主题精准。

- 报告基于截断的实证样本，规模虽含括中等Token数量，若扩展至更长循环或更动态环境，结论可能需要再验证。

• 没有对市场冲击性风险和套利执行失败成本进行讨论，可能限制实际应用。

- 理论利润假设手续费固定，未考虑手续费动态变化的影响。

---

7. 结论性综合

本报告从理论和实证层面系统研究了Uniswap V2套利循环中如何最大化“货币化套利利润”，重点突破了传统仅针对于特定Token套利利润计算的局限，创新地提出MaxMax和凸优化策略。

主要结论包括：

• 传统策略及基于最高CEX价格Token入手的MaxPrice策略普遍不能保证获得最大化利润，容易低估套利收益。
• MaxMax策略通过循环尝试每个Token作为起点，数学和实证证明其利润始终不低于传统和MaxPrice策略，计算简单且高效，非常适合实际操作。
• 将MaxMax策略映射为凸优化问题的凸优化策略，理论证明利润优于MaxMax，实证数据表明两策略获利差异极小。凸优化策略计算复杂、耗时长，限制其实用性。
• 综合实证基于2023年Uniswap V2数据验证了上述理论，具体循环结构和Token价格真实反映市场套利情况。
• 报告理论模型的数学基础扎实，辅以详实的图表如函数曲线（图1）、策略利润对比（图2、图3、图5至图10）等，论证严谨直观。
• 未来研究可聚焦理论上量化凸优化策略与MaxMax策略的利润差异，及扩展带风险成本的实际套利模型。

整体而言，本报告为DeFi套利领域带来了基于多Token、多市场价格信息的利润最大化新视角和有效计算策略，促进了理论与实务的结合，具有较高的参考价值和应用前景。

---

附图引用（markdown格式）

• Fig.1（利润最优化示意图）：

• Fig.2（不同起点策略利润对比）：

• Fig.3（凸优化与MaxMax利润对比）：

• Fig.4（Token净套利量三维分布）：

• Fig.5（MaxMax与传统策略利润对比）：

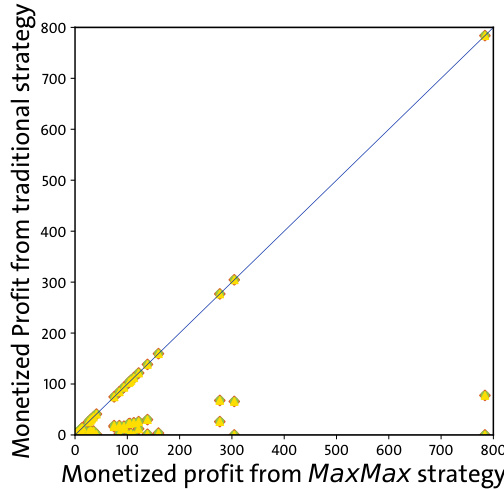
• Fig.6（MaxMax与MaxPrice策略利润对比）：

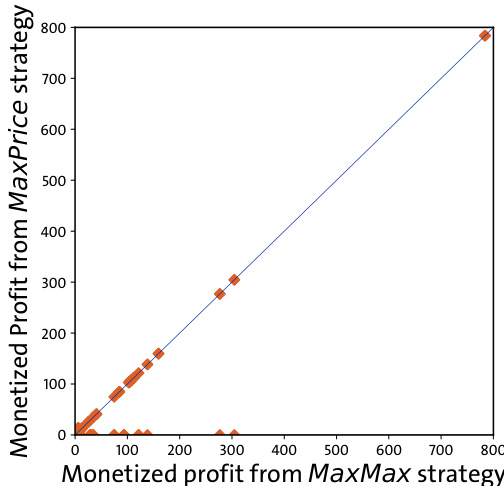
• Fig.7（凸优化与MaxMax策略利润对比）：

• Fig.8（Token套利净量对比）：

• Fig.9（四Token循环传统策略与凸优化策略利润）：

• Fig.10（四Token循环MaxMax与凸优化策略利润）：

---

参考页码

全篇引用[page::0,1,2,3,4,5,6,7]，分段详见结构部分。

报告