金融工程中Q Quant与P Quant的基本定义与区别 [page::0][page::3][page::4]

• Q Quant以推断当前资产公允价值为目标，侧重卖方衍生品定价，数学环境为风险中性概率测度Q，使用连续时间随机微积分和偏微分方程，面对模型校准挑战。

- P Quant以对未来风险和组合收益建模为主，属于买方工作，基于真实概率测度P，采用多元统计分析和计量经济方法处理高维离散时间数据，面临估计难题，重视因子降维技术。

• Q Quant聚焦低维单个证券，P Quant关注整体组合分布和多资产。

Q Quant 与 P Quant 在理论与应用上的交叉 [page::4][page::5][page::6]

• 两者均基于随机过程建模，但Q Quant用连续时间模型（如Levy过程、Ornstein-Uhlenbeck过程等），P Quant则用离散时间模型（如随机游走、ARMA、GARCH）。

- 数值方法分别为分类树和蒙特卡洛模拟，在不同场景下选用：Q Quant对美式期权用分类树，亚式期权用蒙特卡洛；P Quant用分类树设计动态策略，蒙特卡洛估计风险指标如VaR。

• 对冲作为两者交集，P Quant负责构建风险因子中性组合，Q Quant通过计算希腊字母（Greeks）提供风险敏感性，二者相辅相成。

统计套利策略及图示 [page::6]

• 通过Q Quant模型识别证券价格中定价错误，基于价格偏离预测值的alpha信号做多空头，价格逐渐向模型预测收敛。

- 图1展示了价格由当前价向Q模型预测价格回归的空头统计套利示意。

具体随机过程对比表 [page::5]

| 特征 | 离散时间 (P Quant) | 连续时间 (Q Quant) |
|------------|----------------------|-------------------------|
| 基础假设 | 随机游走 | Levy过程（Brownian、Poisson） |
| 自相关性 | ARMA | Ornstein-Uhlenbeck |
| 波动率聚集 | GARCH | 随机波动率模型 |

• P Quant和Q Quant用不同模型捕捉价格特征，分别适应离散和连续时间需求。[page::5]

报告详细分析——《量化研究新思维（二）——P vs Q：金融工程两大分支的异同》

---

一、元数据与概览

• 报告标题： 《量化研究新思维（二）——P vs Q：金融工程两大分支的异同》

- 发布机构： 海通证券股份有限公司研究所

• 发布日期： 2017年4月13日

- 作者及联系方式： 分析师冯佳睿，电话：(021)23219732，邮箱：fengjr@htsec.com

• 主题： 金融工程量化领域中的两大核心分支——Q Quant（衍生品定价）与P Quant（风险与组合管理）的区别、联系及应用分析。

核心论点及信息概括

报告围绕金融工程中的两大量化领域：Q Quant 和 P Quant，系统阐述了两者的基本定义、所处数学环境、面临的挑战、所使用的定量方法及工具，并探讨了它们的交叉领域，如风险溢价计算、随机过程模型、数值模拟方法、对冲策略和统计套利。特别提出：

• Q Quant聚焦“推断现在”，其核心为利用风险中性概率测度在连续时间框架下，通过复杂的数学工具（随机微积分、偏微分方程）完成衍生品的价格校准与定价，主要服务卖方。

- P Quant聚焦“对未来建模”，基于真实概率测度P，采用多元统计及计量经济学技术估计证券联合分布，改善投资组合的风险收益特征，主要服务买方。

• 两者虽有本质差异，但交叉领域尤为丰富，尤其在风险溢价的定义、随机过程模型和对冲策略的实际操作中互为支持。

- 该报告强调，未来金融工程领域两者界限将愈发模糊，合作趋于紧密。

此外，报告附带对市场风险、模型失效风险及国内外市场结构差异风险的风险提示。报告内容丰富，理论基础扎实，侧重于学术与应用实践的结合。[page::0, 3-7]

---

二、逐节深度解读

1. Q Quant——衍生品定价

关键论点

• 定义目标： Q Quant主要解决衍生品的市场公允价值定价问题，即“推断现在”，通过风险中性测度Q，预测衍生品现价。

- 基本数学环境: 基于风险中性概率测度Q，具体表现为连续时间内的鞅过程。

• 主要挑战： 模型的“校准”（calibration），即使模型参数与市场实际观测价格高度符合，确保对新产品的有效定价。

- 常用工具： 随机微积分、偏微分方程。

• 业务定位： 以卖方为主——交易员和市场制造者的核心技术手段。

支撑逻辑与历史沿革

• 报告由Bachelier早期随机过程应用到期权定价，继而Black-Scholes-Merton的几何布朗运动定价模型，至Harrison和Pliska提出的风险中性鞅理论，构成现代金融工程学的理论基石。

- “鞅”的定义说明无套利原则：未来价格在风险中性测度下的期望值等于现价，说明风险调整后期望价格稳定，是经典衍生品定价的核心假设。

• Q Quant的模型维度低，因为专为单一衍生品设计，强调精确估值和动态调整。

关键数据点

• 表 1总结了目标、数学环境、随机过程类型、数据维度、数学工具及主要挑战，凸显该分支的专注点。

分析

该章节详细梳理了Q Quant的发展脉络和基本特征，强调其数学复杂性与专注卖方市场的定位。校准问题尤为关键，体现市场和数学模型的结合难点。[page::3]

---

2. P Quant——风险与组合管理

关键论点

• 定义目标： P Quant关注“对未来建模”，基于真实概率分布P，用统计和计量方法估计未来证券收益状况，优化组合配置，提升收益-风险关系。

- 数学环境： 真实概率测度P，离散时间序列分析。

• 主要挑战： 估计（estimation），尤其是联合分布的高维估计与降维处理。

- 数学工具： 多元统计分析、计量经济学方法，降维方法如线性因子模型至关重要。

• 业务定位： 买方机构（投资者、资产管理者）核心职责。

支撑逻辑

• 理论基础来源于Markowitz均值-方差理论，随后CAPM、APT模型为风险和资产定价提供统计定量框架。

- 实际操作中，真实分布P难以直接获取，需依赖历史数据和市场信息进行估计，且数据是离散时间收集，增加了分析的复杂度。

• 降维技术是解决高维股票联合估计的关键，有助于合理管理投资组合的风险。

- 市场人才需求转换，P Quant课程逐渐纳入金融工程硕士课程，表明P Quant重要性上升。

关键数据点

• 表 2对P Quant的目标、数学环境、随机过程、数据维度、数学工具及挑战进行了系统总结。[page::4]

分析

P Quant从更多的实证统计出发，致力于未来风险收益建模，其高维度和真实世界测度带来了数据估计挑战。资金管理的买方机构大量依赖此分支研究实现资产配置决策。技术工具与Q Quant相比更偏向统计学与计量经济学方向。[page::4]

---

3. P Quant和Q Quant的共同点及交叉

本部分通过分子小节细致展开两大分支的交集。

3.1 风险溢价

• 数学上，风险中性测度Q与真实测度P的转换由风险溢价决定。

- 估计风险溢价是当前极具挑战但至关重要的课题。

3.2 随机过程

• 两者共同依赖随机过程建模，但Q Quant主用连续时间模型，P Quant主用离散时间模型。

- 重点随机过程对比如表3展示：

| 特征 | 离散时间（P Quant） | 连续时间（Q Quant） |
|------------|---------------------|-----------------------------|
| 基础假设 | 随机游走 | Levy过程（布朗运动、泊松过程）|
| 自相关性 | ARMA模型 | Ornstein-Uhlenbeck过程 |
| 波动率聚集 | GARCH模型 | 随机波动率模型 |

• 离散随机游走是P Quant利率和股票价格建模的基准，布朗运动为Q Quant期权定价基础。

- 自相关的ARMA及其连续版本Ornstein-Uhlenbeck广泛使用于时间序列与债券定价。

• 波动率聚集使用GARCH（P Quant）和随机波动率模型（Q Quant）。

3.3 数值方法

• 分别介绍分类树和蒙特卡洛模拟两种数值方法。

- 分类树结果呈指数增长，适合重要决策与美式期权定价。

• 蒙特卡洛路径数固定，更适合风险管理及亚式期权。

3.4 对冲

• 对冲作为P Quant的风险管理概念，依赖Q Quant计算的“希腊字母”（Greeks）确定具体对冲规模。

- 该部分详细解释希腊字母中的delta是期权对标的的敏感度，指导卖空对冲量。

• 体现P Quant与Q Quant工具互相依赖和相辅相成。

3.5 统计套利

• 统计套利案例细化两者如何结合使用：Q Quant模型确定定价误差，P Quant基于误差推断alpha构建多空头策略。

- 附有图1，描绘错误定价证券价格随时间向Q Quant预测价格回归的过程。



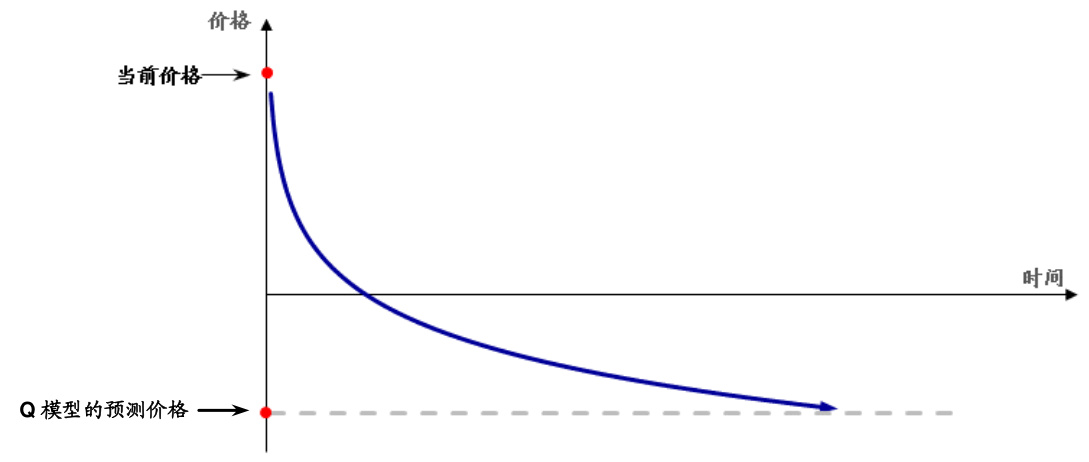
示意图清晰表明，当前价格偏离模型价格，未来价格将在统计套利交易压力下逐渐收敛，系统化套利策略的基本逻辑。

整体来看，三节重点揭示两者理论差异下的协同互补关系，体现不同数学架构之间的桥梁搭建。[page::4-6]

---

三、图表深度解读

表1 Q Quant——衍生品定价

| 项目 | 内容 |
|------------|---------------------------|
| 目标 | 推断现在（extrapolate the present）|
| 数学环境 | 风险中性概率测度Q |
| 随机过程 | 连续时间鞅 |
| 数据维度 | 低 |
| 数学工具 | 随机微积分、偏微分方程 |
| 面临挑战 | 校准（calibration） |
| 业务定位 | 卖方（sell-side） |

解读： 显示Q Quant侧重现值定价，数学工具高阶复杂，针对低维单品精准模型构建，突出校准重要性。工具与业务定位高度匹配[page::3]

---

表2 P Quant——风险与组合管理

| 项目 | 内容 |
|------------|---------------------------|
| 目标 | 对未来建模（model the future）|
| 数学环境 | 真实概率测度P |
| 随机过程 | 离散时间序列 |
| 数据维度 | 高 |
| 数学工具 | 多元统计分析 |
| 面临挑战 | 估计（estimation） |
| 业务定位 | 买方（buy-side） |

解读： 明确P Quant面对高维数据，对未来收益及风险的整体建模，依赖大量统计与计量分析，估计难度突出。业务端强调资产管理审核与决策[page::4]

---

表3 P Quant和Q Quant常用的随机过程对比

| | 离散时间 | 连续时间 |
|-------------|---------------------------|-----------------------------|
| 基础假设 | 随机游走 | Levy过程（布朗运动、泊松过程） |
| 自相关性 | ARMA | Ornstein-Uhlenbeck过程 |
| 波动率聚集性 | GARCH | 随机波动率模型 |

解读： 该表浓缩两大领域随机过程的核心模型，展示它们如何在不同时间框架和过程结构下对应类似的市场行为，具体技术选择体现了买方和卖方的建模需求差异[page::5]

---

图1 空头统计套利示意图

图中以价格为纵轴，时间为横轴，显示当前价格高于“Q模型预测价格”，通过时间推移价格向模型价格收敛。

解读： 视觉化说明统计套利实践步骤：先识别错误定价，后基于该偏差配置策略，最终通过市场行为推动价格调整，反映P Quant alpha和Q Quant模型预测的结合。进一步强化了两大分支的相互依存关系。[page::6]

---

四、估值分析

报告未包含单独估值模型对具体证券的估值说明，更多关注两类量化范式的理论内涵及应用区别。
不过，Q Quant本质上就是估值体系的核心，实现衍生品公允价值的精确定价，P Quant通过建模未来收益分布，决定仓位配置，间接实现资产的“市场估值”优化。报告在此方面更多为理论探讨，未给出具体数值估计或模型估值案例。

---

五、风险因素评估

报告明确提供了三类风险提示：

• 市场系统性风险： 无法通过分散投资规避的宏观经济及市场整体波动风险。

- 模型失效风险： 量化模型无法完全捕捉真实市场行为，假设偏离可能导致定价或风险管理失误。

• 海外与国内市场结构差异风险： 国际市场与中国市场的制度和结构差异可能影响模型迁移和应对策略有效性。

风险提示明确，且强调数量化模型的局限，提醒投资者和使用者理性看待模型输出，且报告声明不含主观调整，保证客观性。[page::0, 6]

---

六、批判性视角与细微差别

• 理论与实际的张力： 报告虽清晰区分了Q Quant和P Quant的测度与时间结构不同，但对两者在实际市场中的动态融合仅做浅显描述。真正的量化投资实践可能更多依赖跨领域混合模型，报告留有理论基础解释不足的空间。

- 估计风险与校准难题强调合理，但解决方案未深究： 校准和估计的困难是量化研究的老问题，报告未提供新颖路径，更多是理论总述，缺少创新见解。

• 部分数学原理非常浓缩，对非专业读者理解门槛高，未配备较完整的解释或示例： 比如鞅过程等，可能需要进一步展开。

- 报告中风险提示细节较泛，未具体列出风险发生概率或缓解措施。

• 总体表达较为学术体系化，忽略了当时中国市场特有环境对P Quant和Q Quant各自适用度和限制的更深入讨论。

尽管如此，报告在基础阐释和整体框架呈现上还是十分清晰和规范的，适合中高级金融工程、量化研究人员阅读。

---

七、结论性综合

本报告全面梳理了金融工程中两大量化核心分支——Q Quant（风险中性测度的衍生品定价方向）与P Quant（真实概率测度基础上的风险与组合管理方向）的根本差异和联系。核心观察点包括：

• 目标差异明确： Q Quant注重估值与市场价格“推断现在”，P Quant致力于“对未来建模”，优化风险和收益。

- 数学环境与技术工具差异鲜明，Q Quant侧重连续时间风险中性鞅，P Quant更多采用离散时间统计模型。

• 数据处理维度不同，Q Quant围绕单一标的低维建模，P Quant面对高维联合分布估计及降维。

- 交叉领域成为两者共融的桥梁，风险溢价、随机过程模型及数值模拟方法均有实际重叠。

• 对冲策略和统计套利实践尤为体现两者深度嫁接，例如Q Quant的希腊字母用于P Quant风险管理。

- 图表和模型总结清晰支撑了理论论点，图1生动演示统计套利中价格向模型价收敛的动态过程。

• 风险提示虽较为概括，但恰当提醒模型和市场的多重不确定性。

总体而言，报告以学术严谨的态度科学系统地展现了量化研究领域P与Q两大分支的内在特性及相互关系，传递了未来两者融合趋势不可避免的信息。该报告适用于金融工程研究人员、量化投资经理及相关领域学习者，为理解现代量化方法论提供了扎实的理论框架和知识地图。

---

参考溯源

• 量化研究新思维（二）正文主要内容及论述，见第0至第7页 [page::0-7]

- 关键图表与图形解读，见第3页至第6页 [page::3-6]

• 相关数学模型及风险提示，见第0页及第6页 [page::0, 6]

---

结束语

该报告系统总结了金融工程领域内两个重要量化分支的理论基础、实践应用及未来发展趋势，兼具理论性与实用性，是理解和研究现代金融量化方法的重要参考文献。

报告