研究背景与模型框架 [page::0][page::1][page::4][page::5][page::6]

• 研究波动率方差期权，标的变量为资产收益的年化实现方差，可与方差互换关联。

- 采用局部随机波动率模型描述资产和波动过程，模型参数满足一定有界性和Lipschitz条件。

• 期权支付与对数价格的二次变差联系，着重分析短期(T→0)极限下的价差行为。

- 遵循大偏差理论，推导样本路径大偏差率函数，形式为一个二维变分问题。

远价（OTM）期权短期渐近及变分问题解析 [page::7][page::8][page::9]

• 远价期权价格的对数被T倍放大后收敛于率函数的负值，该率函数为二维变分优化的最优值。

- 当资产价格和波动过程无相关(ρ=0)时，变分问题能简化为一维优化，解析表达由局部波动率函数和波动率过程的变分问题组合组成：

• 公式中涉及解方程确定函数$Gc(z), Gp(z)$满足积分关系，优化变量为聚合路径指标$z$。

- 此解连接了当ρ=0时的波动率方差期权价格渐近与亚式期权研究的已知成果。

• 对于非零相关，得到率函数的上下界估计，参数屏蔽相关影响。

完全相关与完全负相关特殊情形 [page::14][page::15]

• ρ=±1时，变分问题简化为单变量变分问题，可进一步转换为局部波动率模型亚式期权的变分问题，具有解析解。

- 给出显式定义的变换函数$\mathcal{F}_\pm$，将率函数问题降为单个函数上的优化。

率函数在平价点附近展开及ATM期权[page::16][page::17]

• 利用局部波动率函数及波动率波动率在平价点处的泰勒展开，给出率函数近似二次及更高次展式。

- ATM期权价格短期尺度为$O(\sqrt{T})$，不同于远价期权的指数衰减。

• ATM期权价格主导项有显式闭式形式，与局部随机波动率相关联。

数值验证及具体模型案例分析 [page::18][page::19][page::21][page::22][page::24]

• 采用Tanh型局部波动率函数，设置常数波动率波动率，数值求解变分问题。

- 比较了解析展开与精确数值解及蒙特卡罗模拟结果，验证率函数及隐含波动率的准确性。

• 提供了隐含波动率的上下界，覆盖不同相关系数。

- 蒙特卡罗模拟显示渐近公式对1个月及1日期权均较好拟合，短期（1日）拟合更佳，验证了理论预期。

量化模型与理论贡献

• 开创性地为局部随机波动率模型下实方差期权的短期极限定价提供系统研究。

- 连接局部随机波动率模型与亚式期权定价的短期极限分析。

• 引入大偏差率函数的变分表达，兼具理论严谨和数值可操作性。

- 提供不同相关条件下的边界估计及特殊解，具备应用推广潜力。

金融研究报告详尽分析报告

---

1. 元数据与概览

• 报告标题：Short-maturity options on realized variance in local-stochastic volatility models

- 作者：Dan Pirjol, Xiaoyu Wang, Lingjiong Zhu

• 发布机构及日期：日期标记为2025年9月16日，具体机构未明，可能为学术研究或金融数学研究团队。

- 主题：探讨局部-随机波动率（Local-Stochastic Volatility, LSV）模型下实现方差衍生品期权（options on realized variance）的短期到期（short-maturity）价格渐近行为。

核心论点与目标

报告主要目的是：

• 推导 LSV 模型中实现方差期权价格在短期到期的渐近行为，针对平价价外（out-of-the-money, OTM）和实值（in-the-money, ITM）期权分别处理。

- 利用大偏差理论（Large Deviations Theory）将OTM情况转化为二维变分问题求解。

• 针对无相关（$\rho=0$）情况，能够明确求解变分问题；相关$\rho\neq0$时给出解的上下界及针对平价问题的展开。

- 数值模拟验证模型与理论结果在小到期时间内的吻合度。

• 给出平价（at-the-money, ATM）方差期权的价格主导项闭式表达。

- 结合市场实际，特别是 CBOE 新推出的基于实现方差的期货及其期权，说明理论结果的市场应用价值。

主要信息传达：

• 建立针对局部-随机波动率模型下实现方差期权的短期价格近似分析体系，填补该领域严谨研究的空白。

- 为实际期权定价与风险管理提供理论基础和计算工具。

---

2. 章节深入解读

2.1 报告引言及背景（第0至1页）

• 定义和基础：通过离散采样对资产价格实现方差$\mathrm{RV}{T,n}$的定义，以及与连续时间下对数资产价格的二次变差$[\log S, \log S]T$关联。

- 讨论离散采样与连续极限的不同： 指出离散版期望不一定收敛至连续版本期望，特别如$3/2$模型。

• 关注点明确：聚焦于连续时间框架下，基于二次变差的实现方差期权短期到期价格的渐近研究。

- 文献空白：此前对 LSV 模型下实现方差期权短期渐近缺乏严格研究。

• 真实市场相关性：介绍2024年CBOE推出的S&P 500实现方差期货及其期权，该报告成果可应用于此类产品定价。

关键词：实现方差期权，短期渐近，大偏差，局部-随机波动率模型。[page::0,1]

2.2 相关文献综述（第2至3页）

• 传统模型回顾：包括Bergomi系列模型、Heston模型、Lévy过程等对实现方差期权的定价方法，其中Laplace变换、半解析公式、有限跳跃过程等方法。

- 离散时间取样影响：理论和实务中实现方差和其期权通常基于离散时间计算，相关的误差和偏差研究也较多。

• 与亚洲期权联系：指出某类模型（马尔科夫随机波动率）实现方差期权与局部波动率模型下亚洲期权等价，后者的短期期权渐近有已有研究。

- 大偏差与短期期权定价工具：提及样本路径大偏差原理及其在亚洲期权和波动率衍生品短期期权价研究中的应用。

对报告意义：本报告拓展并补充了局部-随机波动率模型中的短期期权定价理论，首次系统探讨对应OTM与ATM行为。[page::2,3]

2.3 模型设定（第4至6页）

• 模型形式：LSV 模型定义为：资产价格$St$满足带局部波动率函数$\eta(St)$乘以随机波动率$\sqrt{Vt}$，二者由两独立布朗运动$Wt,Zt$驱动，有相关系数$\rho$；标的波动率过程$Vt$自我演化遵循Itô过程(2.2)。

\[
\frac{d St}{St} = (r-q) dt + \eta(St) \sqrt{Vt} (\rho dZt + \sqrt{1-\rho^2} dWt), \quad \frac{d Vt}{Vt} = \mu(Vt) dt + \sigma(Vt) dZt
\]

• 期权标的含义：期权支付与$\frac{1}{T}\int0^T Vs \eta^2(Ss) ds$相关，实际为对数价格的二次变差。

- 假设：
- $\eta(\cdot),\mu(\cdot),\sigma(\cdot)$均统一有界（Assumption 1），
- $\eta$由减函数保证金融的杠杆效应，
- $\eta$和$\sigma$满足Lipschitz条件（Assumption 2），且正下界存在（Assumption 3）。

• 方差互换合约公平行权价$FV(T)$定义为期望实现方差。

- 期权类别与moneyness判定：Otm/Itm/ATM由$K$与$FV(T)$比较，且短期极限$moneyness$以$V0\eta^2(S0)$衡量。

• 讨论绕过了ITM情形，可通过套利关系处理。

提醒：当$\eta(x)\equiv1$时，该LSV会退化为纯随机波动率模型，此时实现方差期权价等价于局部波动率模型下的亚洲期权价。[page::4,5,6]

2.4 主要结果（第7至17页）

2.4.1 OTM案例定理（Theorem 4）

• 表述：短期极限下的OTM方差期权价格呈指数型衰减，其对数定价乘以$T$的极限等于负的变分问题定义的速率函数$\mathcal{T}{\rho}(S0,V0,K)$。

- 该速率函数用二维函数$(g,h)$的变分问题表示，约束积分$\int0^1 e^{h(t)} \eta^2(e^{g(t)}) dt=K$。

• 对$\rho=\pm 1$（完美相关/反相关）情况有特例分析。

- Remark：Heston等某些模型不满足强假设，但变分框架依旧可用，且市场行情吻合度较差不纳入重点。

2.4.2 $\rho=0$无相关解（Proposition 6）

• 在无相关情况下，变分问题分离简化为单变量变分问题，封闭形式解出。

- 关键是内变量$z$的优化，$z$表示波动率路径的均值，另一变量$g$关联局部波动率路径，$Gc(z)$满足包含积分方程。

• ATM选项（$K=V0\eta^2(S0)$）速率函数为零，符合法律大数定律。

- 具体函数形式复杂，涉及积分表达式和优化。

• 优化结果确定了最佳轨迹$(g0,h0)$的表达形式。

2.4.3 非零相关$\rho\neq0$（章节3.2.2）

• Euler-Lagrange方程给出隐式方程组，难以显式求解。

- 通过直观及数学技巧得到$\mathcal{T}\rho$的上下界，均围绕$\rho=0$案例速率函数展开（Propositions 11、12）。

• $\rho$趋近于1或-1时，单变量变分问题解决方案可引出完美相关极限（Proposition 14）。

- 近相关性时，提出可行上界$\mathcal{T}\rho \leq$某单函数最小化表达。

2.4.4 ATM情形（Theorem 20）

• 短期期权ATM市价的主要贡献来自中心极限定理范畴内的波动，价格不再指数小，而是规模为$O(\sqrt{T})$。

- 公式中明确指出ATM期权价格的渐近表达与局部波动率函数的一阶导数、中枢点值及参数$\sigma(\cdot)$一起决定价格震荡幅度。

2.4.5 速率函数ATM附近展开（Proposition 19）

• 基于局部波动率$\eta(\cdot)$和波动率波动率$\sigma(\cdot)$在现货点处二阶泰勒展开，构建以对数价外度$x=\log(\frac{K}{V0\eta^2(S0)})$为小参数的二阶及三阶展开。

- 给出展开后速率函数显式式子，包含多个参数组合系数$\beta0,\beta1,\beta2$，并提供最优路径的导数表达。

• 当$\eta(\cdot)\equiv1$时退化为已知亚洲期权速率函数。

---

3. 图表与数值结果深度解读（第18至24页）

3.1 收敛性与速率函数精确解的检验

• 利用“Tanh”局部波动率模型对无相关情况$\rho=0$的精确变分资源结果和基于对数价内度的渐近展开进行数值对比。

- 图1左：速率函数$\mathcal{T}0$随对数价内度$x$曲线（黑色实线），与三阶渐近展开（虚线）对比，说明展开仅在ATM附近较准确。

• 图1右：对应的期权隐含波动率曲线。实线为精确解，点线为渐近线。

- 结果表明，渐近展开对于价格接近ATM点的期权较好，但远离时误差显著。

3.2 相关性对波动率区间的边界控制（图2）

• 边界1（Proposition 11）：用$\rho=0$速率函数对任意$\rho$区间进行上下界估计，图中以蓝色和红色实线呈现。

- 边界2（Proposition 13）：提供另一下界，基于局部波动率模型下的亚洲期权速率函数（蓝色虚线）。

• 图2显示，对于$\rho=\pm0.5$和$\rho=\pm0.7$的情形，上下界有效近似，且边界独立于$\rho$符号。

- 实际逼近中，渐近近似偶有超出界限，提示边界并非全局极紧。

3.3 蒙特卡洛数值对比（图3、4与表1）

• 设定Tanh模型参数，进行不同$\rho$取值下的实现方差期权隐含波动率蒙特卡洛模拟。

- 图3为1个月期权，图4为1个交易日期权（更短），模拟点与渐近理论线高度吻合，但1个月期权有轻微偏差，1日期权拟合更佳。

• 通过数值模拟验证理论推导的准确性和适用期限，表明次阶$O(T)$修正是误差源。

- 表1罗列ATM隐含波动率水平和斜率等数值供参考。

---

4. 估值分析

• 报告主要使用大偏差理论构造实现方差期权价格短期期限行为的估值框架。

- 变分问题的速率函数$\mathcal{T}\rho$对应价格的指数速率，函数的参数反映局部波动率$\eta(\cdot)$、波动率过程特征$\sigma(\cdot),\mu(\cdot)$及相关$\rho$。

• 对于闭式解析难解问题，提供边界估值及数值优化技巧，平价ATM附近提供二阶展开便于实际应用。

- 估值方法实际上将期权价转化为对应速率函数的解，加上Black-Scholes定价框架，将实现方差期权近似为带非标隐含波动率的BS期权。

---

5. 风险因素评估

报告未直接以“风险因素”形式总结，但从理论及数值结果分析，隐含以下风险及限制：

• 模型假设敏感性：尤其对$\eta(\cdot), \sigma(\cdot)$的界限及连续性要求较强，Heston型等模型某些参数不满足。

- 离散采样误差：现实中实现方差按日采样，离散和连续模形间存在非统一收敛问题，需逐模型检验。

• 相关性极限处理复杂：$\rho \to \pm 1$时模型简化，但接近极限时数值稳定性和估值准确度有挑战。

- 数值计算复杂度：变分问题涉及微分方程边界条件，尤其多参数情况下求解需数值方法，误差控制需验证。

• 渐近展开有效区间有限：ATM附近表现良好，对较远价外期权拟合误差增大，提示要谨慎使用展开结果。

---

6. 批判性视角与细微差别

• 研究假设框架较为理想，实际市况中模型适用范围及参数选择存在一定不确定性。

- 相关系数$\rho$的变化对结果影响显著，报告在$\rho=0$和极端$\rho=\pm 1$情况提供较全解，中间区间仅有界估计，可能影响实际定价精度。

• 离散采样价格与连续极限的偏差未深入定量分析，但文中已有提醒，提示实际应用中需谨慎。

- 展开式截断所带来的误差在数值对比中表现较好，提示足够用于近ATM期权近似，但对价外期权得进一步分析。

• 虽然模型复杂，金融假设较理想，报告在数学严谨性上较完备，且配套数值模拟支撑。

---

7. 结论性综合

本报告系统探讨了局部-随机波动率模型中短期期限实现方差期权的价格行为，关键结论和见解包括：

• 针对OTM期权，价格在短期内呈指数型小（以期权价格对数乘以期限$T$收敛于负的速率函数），而该速率函数为二维函数的变分问题。

- 无相关$\rho=0$时可简化为单变量变分问题，并可封闭表达速率函数和最优路径。

• 相关$\rho \neq 0$时，通过变分法与Euler-Lagrange方程求得上下界，极端$\rho = \pm 1$时的解析解与局部波动率亚洲期权速率函数对应。

- ATM期权表现与OTM不同，短期价格为$O(\sqrt{T})$量级，反映中心极限定理范畴，给出了显式主导项公式。

• 对率函数ATM点进行对数价内度$x$的二阶展开，给出实际定价便利的近似式和路径修正项。

- 报告配合“Tanh”局部波动率模型进行数值模拟验证，模拟结果支持理论速率函数和隐含波动率展开，说明该方法在实际市场标的下有很好的应用潜力。

• 通过数值测试，证明对OTM期权价格的渐近展开对ATM附近有效，边界估计对于一般$\rho$控制风险具有指导意义。

{{@markdown}}



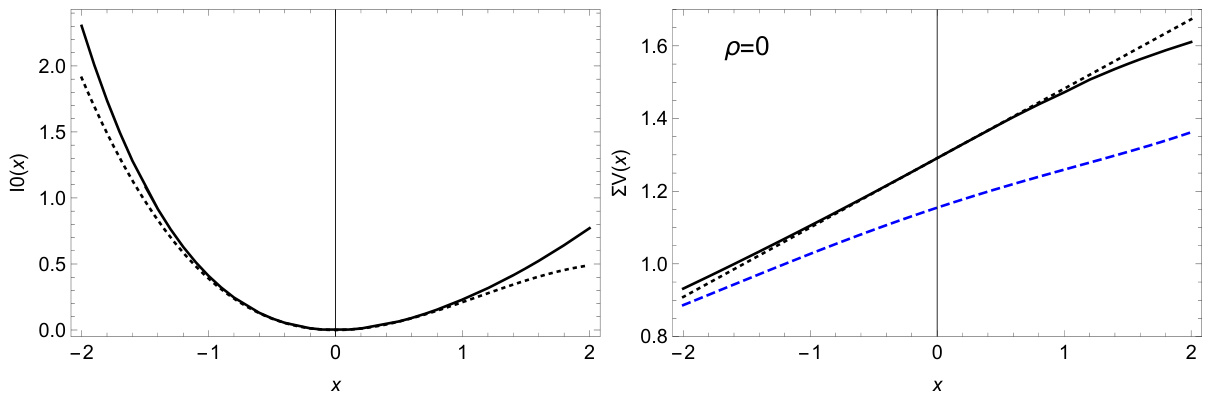
图1：左图为精确速率函数$\mathcal{T}_0$与三阶展开模型的对比，右图为对应隐含波动率曲线，验证了模型在ATM附近的拟合精度。



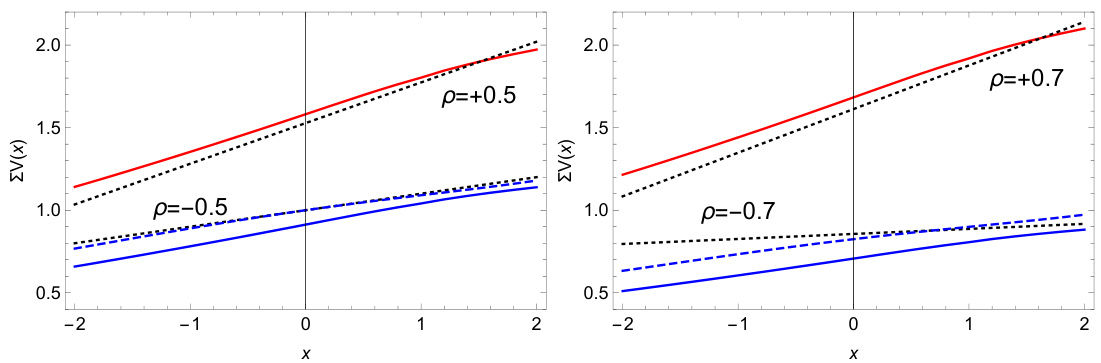
图2：不同相关系数$\rho=\pm0.5$与$\rho=\pm0.7$时，隐含波动率上下界（Proposition 11）及基于局部波动率亚洲期权速率函数的下界（Proposition 13）与渐近展开对比，显示出界估计具实用性。



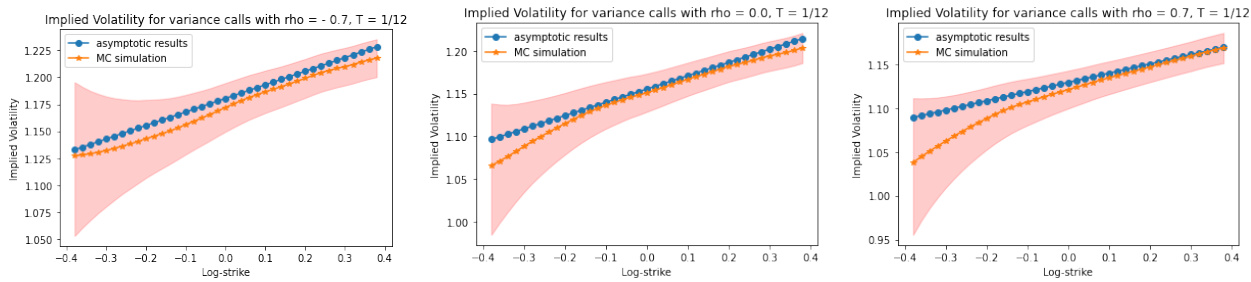
图3：1个月期限下不同$\rho$时期权隐含波动率的蒙特卡洛模拟（橙点）与渐近结果（蓝点）对比，展示渐近理论的实际有效性。



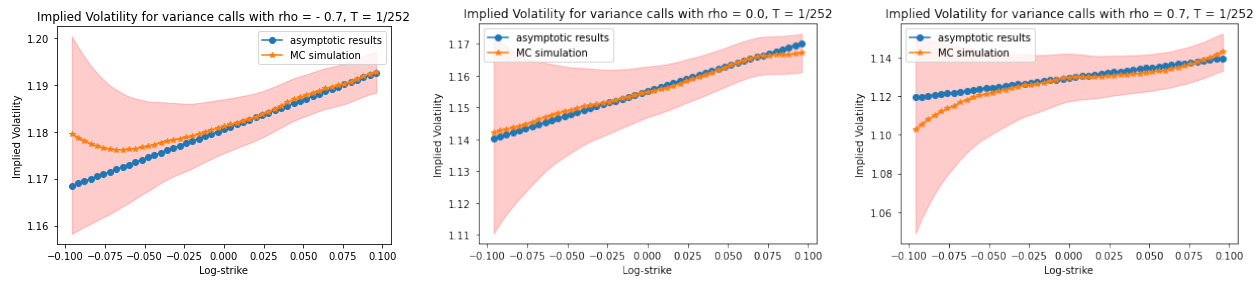
图4：1交易日期限下隐含波动率蒙特卡洛模拟与渐近理论对比，拟合更为精确，凸显渐近结果对短期限的适用性。

{{/markdown}}

---

总结

这份报告严谨地建立了LSV模型下实现方差期权的短期期限定价理论，采用大偏差方法提炼出结构清晰的二维变分问题，从而揭示OTM和ATM期权价格截然不同的渐进行为。其递归推导的解析和数值结论为实际金融工程中实现方差期权的定价和风险管理提供了理论支撑。报告配合详尽数值模拟，验证理论准确性，尤其在无相关或弱相关情况下表现突出，切实填补学界对于LSV模型复杂结构下短期期权定价理论的空白。

本报告贡献了可操作性强的工具，有望指导实际市场上基于实现方差的期权和期货产品的定价策略，亦为相关金融衍生品建模和波动率结构解析提供坚实基础。

---

【本文引用页码】[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]

报告