Kelly策略基础及核心原理 [page::1][page::3][page::4]

• Kelly策略依据胜率和盈亏比，计算最优资金分配比例，实现资本增值速度最大化且防止破产。

- 核心公式包括巴菲特形式f*=p−q和索普形式F=W−(1−W)/R。

• Kelly策略等同于对数效用最大化和几何增长率最大化，是一种基于概率优势的重复投资策略。

贝努利分布下的Kelly行业配置策略 [page::6][page::7][page::8]

| 行业 | 胜率 | 上涨时涨幅 | 下跌时跌幅 | Kelly比例 | 预期几何增长 | 实际几何增长 | 差值 |
|----------------|--------|------------|------------|-----------|--------------|--------------|--------|
| 农林牧渔 | 57.62% | 3.68% | -4.28% | 8.32% | 0.30% | 0.23% | 0.07% |
| 采掘 | 48.75% | 4.31% | -3.84% | 3.02% | 0.05% | 0.05% | 0.00% |
| 化工 | 53.74% | 3.35% | -3.68% | 2.87% | 0.04% | 0.03% | 0.00% |
| …… | ……… | …… | …… | …… | …… | …… | …… |
| 综合 | 55.68% | 3.83% | -4.14% | 7.72% | 0.28% | 0.22% | 0.06% |

• 贝努利分布假设下，Kelly策略在多个行业中表现出正的预期收益，组合年化收益率达约37%（一级行业），56.73%（二级行业），最大回撤控制在10%以下。

• 择时优势显著，策略胜率超过70%，显著超越沪深300基准。

对数正态分布及无分布假设下的Kelly策略及比较 [page::9][page::10][page::11][page::12][page::14][page::15]

• 对数正态分布模型下，Kelly优化转化为均值-方差优化问题，组合权重通过协方差逆矩阵计算得出。

- 与MVP（最小方差组合）策略对比，Kelly组合预期收益和几何增长率更高，适用于长期优胜的资产配置。

• 无分布假设下，Kelly策略通过对数收益近似，依然实现较高的年化回报（超50%），但波动率和最大回撤明显较高。

Kelly策略的局限与改进——Fractional Kelly策略 [page::16]

• Kelly策略对波动和风险的惩罚不足，为此采用Fractional Kelly策略调整风险厌恶参数γ，降低持仓比例。

- 不同γ值对回测结果影响明显，较高γ对应更低收益及回撤。

| Gamma | 财富终值 | 交易胜率 | 年化收益率 | 年化波动率 | 夏普比率 | 最大回撤 |
|-------|----------|----------|------------|------------|----------|----------|
| 10 | 1.74 | 58.68% | 17.97% | 13.63% | 1.06 | 12.07% |
| 20 | 1.63 | 59.28% | 15.65% | 10.06% | 1.20 | 7.59% |
| 100 | 1.44 | 58.68% | 11.43% | 7.88% | 1.03 | 5.39% |

研究总结及策略建议 [page::1][page::17]

• Kelly策略提供高年化收益及较优超额收益能力，但波动及最大回撤较大，风险分散能力有限。

- 策略长期优势明显，但短期近似均值方差组合，适用风险厌恶系数为1的投资者。

• 推荐采用Fractional Kelly策略或结合高波动标的，提升风险控制能力，应用于行业轮动配置中获益显著。

国泰君安2014年中基于Kelly公式的行业配置策略研究报告详尽分析

---

一、元数据与报告概览

• 标题： 基于Kelly公式的行业配置策略——国泰君安2014年中金融工程投资策略

- 作者： 刘富兵

• 发布机构： 国泰君安证券股份有限公司

- 发布日期： 2014年5月27日

• 研究主题： Kelly公式及其在行业配置中的应用，重点针对股票市场内不同行业的投资比例优化，结合不同概率分布假设（贝努利、对数正态及无分布假设）进行策略设计与回测。

核心论点及传达：

报告主要阐述Kelly公式在投资组合构建中的理论基础与实操应用，提出通过Kelly策略实现资本的几何增长率最大化，能够显著超越传统投资组合管理方法（如均值方差模型），并结合具体数据分析其在中国A股一级及二级行业上的应用效果。报告最终指出，虽然Kelly公式理论上有极佳的资本增长效果，但实际应用时需要权衡波动性和回撤风险，建议采用分数Kelly策略或集中于高波动资产以实现更优风险调整收益。总体，作者对Kelly策略持肯定态度，提出其在长期及高收益率条件下优于传统模型，适合金融工程领域投资策略实践。[page::0,1]

---

二、逐节深度解读

2.1 投资要点及Kelly策略基础（第1页）

报告开篇详细介绍Kelly策略的本质和投资组合应用的逻辑：

• Kelly策略适用于“具有优势的重复游戏”，能最大化资本增值速度且保证不破产；

- Kelly公式有两种主要形式：(1)简单形式（f=p-q，即胜率减去败率）；(2)更复杂形式，涉及胜率W与盈亏比R的函数；

• 应用场景覆盖资金分配和投资组合构建；

- 报告指出，Kelly策略在贝努利分布、对数正态分布和无分布假设下均可实施，并获得了年化收益超40%、胜率超60%的显著收益表现，但波动率和最大回撤均较大（约20%区间），且风险分散能力偏弱；

• 进一步指出Kelly策略等同于几何增长率最大化，也等同于对数效用最大化，并且在短期或收益率微变时相当于风险厌恶系数为1的均值方差组合；

- 缺陷在于对波动惩罚不足，提出两种调整方案：分数Kelly策略（提高风险惩罚权重）或选择高波动标的资产以获得更优结果。此内容为策略设计的核心指导思想。[page::1]

2.2 Kelly公式背景与理论推导（第3至5页）

• Kelly公式首次由John Kelly提出，旨在“重复性游戏中最大化资本几何增长率”，具备“资本不破产”保障；

- 介绍了简单版巴菲特形式f = p - q和索普形式F = W - (1-W)/R，明确胜率与盈亏比共同作用于资金分配比例计算；

• Kelly策略应用于资金分配与投资组合，多资产投资状态下通过最大化对数收益期望，计算最优权重；

- 讨论了该方法与著名投资者（香农、索普、巴菲特）的关联，及资本管理实务中的争议，强调Kelly准则优于传统Markowitz组合理论，长周期内应追求几何平均收益最大化，但短期则表现不一；索普强烈支持Kelly法以控制极端风险；

• 学院派（如萨缪尔森）对该理论持批判态度，认为存在假设不合理问题，体现凯利策略在学术界和实战的不同认知。[page::3,4,5]

2.3 贝努利分布下的Kelly策略（第6至8页）

• 假设单资产收益为贝努利分布（上涨概率p，下跌概率q，盈亏比WL），投资者通过最大化预期对数收益推导出最优投资比例公式：

\[
f^{} = \frac{pWL - q}{WL}
\]

• 产业配置以此模型为基础，对申万一级行业进行投资比例优化，列出各行业胜率、涨跌幅、Kelly比例及预期与实际几何增长率。

- 表格显示医药生物、家用电器、信息设备及农林牧渔等行业Kelly比例较高，预期收益也相对较优，虽存在实际收益略低于预期现象，但总体符合预期模式；

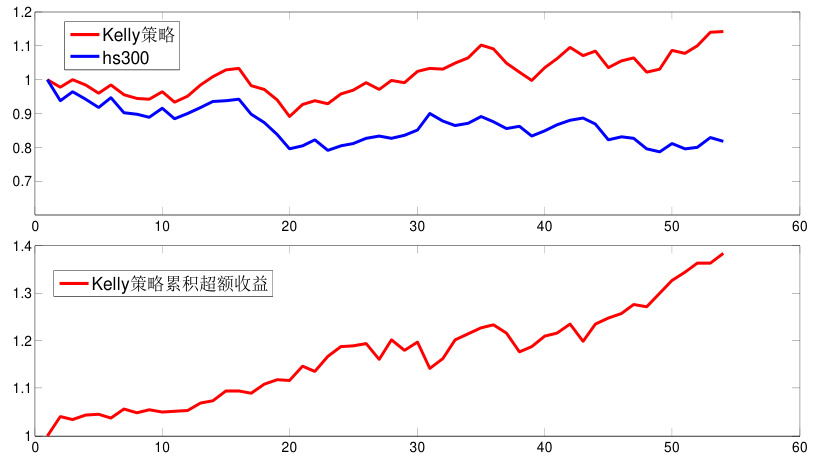
• 对比沪深300指数的贝努利Kelly策略回测显示财富终值达到1.38（一级行业），交易胜率71.7%，年化收益率37.47%，夏普比率2.42，最大回撤仅4.96%，相对稳健；

- 在二级行业上表现更佳，财富终值1.55，胜率76.47%，年化收益56.73%，最大回撤约9%。
这些数据支持Kelly策略在实际应用中收益颇丰，但波动和回撤仍不可忽视。[page::6,7,8]

2.4 对数正态分布下的Kelly策略（第9至13页）

• 假设股票价格服从几何布朗运动，收益率服从对数正态分布，组合年化几何增长率表达为：

\[
g_{P} = \boldsymbol{w}^\top \boldsymbol{\mu} - \frac{1}{2} \boldsymbol{w}^\top \Sigma \boldsymbol{w}
\]

• 以最大化年化几何增长率为目标进行投资组合权重优化，结合拉格朗日乘数法求解，权重表达式为

\[
\mathbf{w}^ = \Sigma^{-1} \left( \boldsymbol{\mu} - \lambda \mathbf{e} \right)
\]
并连续推导组合的期望收益和方差；

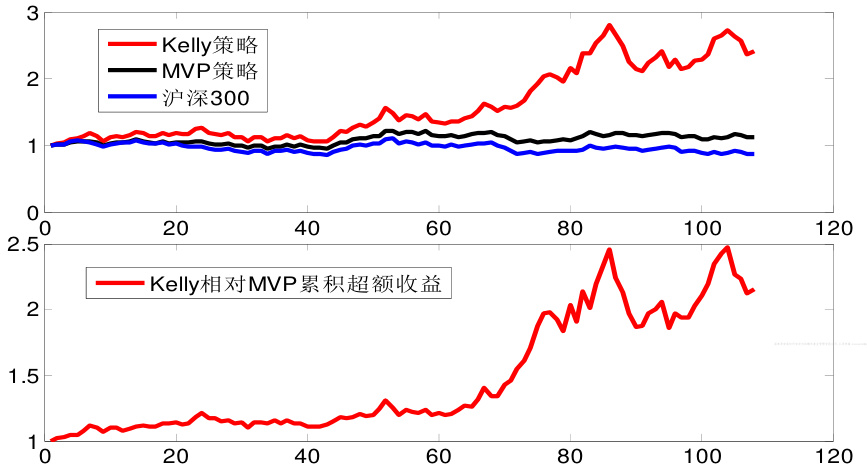
• 进一步比较Kelly组合与均值-方差模型中方差最小组合（MVP）差异，Kelly组合多了针对期望收益的调整项，使其在长期投资中表现出更高的几何增长率；

- 回测数据层面，Kelly策略在一级行业财富终值达到2.78，年化收益61.29%，最大回撤约23.87%，二级行业财富终值2.32，年化收益48.14%，最大回撤18.4%；

• MVP策略同一时期财富终值仅1.29，年化收益12.56%，最大回撤3.79%，显示Kelly策略拥有更高收益但伴随更大风险；

- 投资回报曲线显示Kelly策略明显优于MVP及沪深300指数，累计超额收益不断扩大；

• 交易胜率和夏普比率同样显示Kelly组合优于MVP组合。[page::9,10,11,12,13]

2.5 无分布假设下的Kelly策略（第14至16页）

• 通过泰勒展开式推导，近似等同于最大化投资组合的对数期望收益与波动权衡，形成无特定分布假设的Kelly优化模型

- 优化目标表达式:
\[
\ln(1 + \mathbf{w}^\top \boldsymbol{\mu}) - \frac{1}{2} \frac{\mathbf{w}^\top \Sigma \mathbf{w}}{(1 + \mathbf{w}^\top \boldsymbol{\mu})^2}
\]

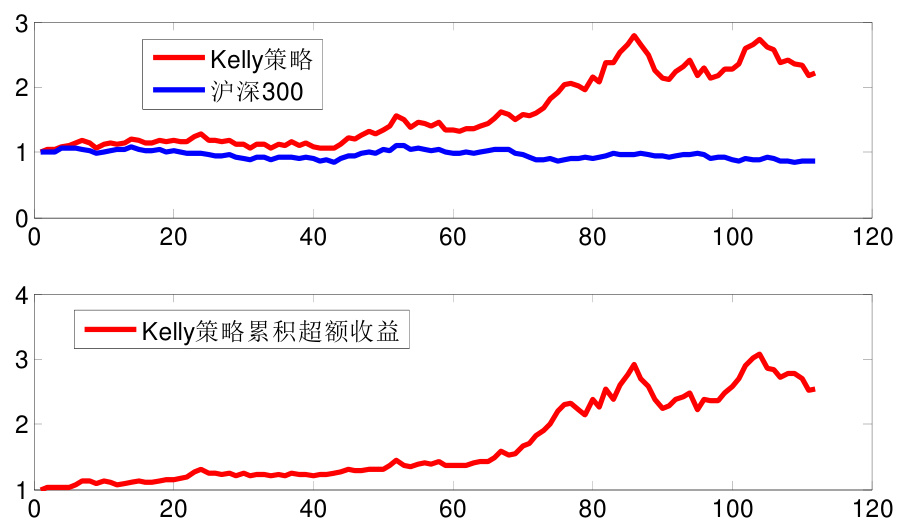
• 无分布假设更贴近现实市场，且得到的策略收益表现与对数正态分布下相似，回测财富终值2.53，年化收益52.03%，最大回撤23.87%；

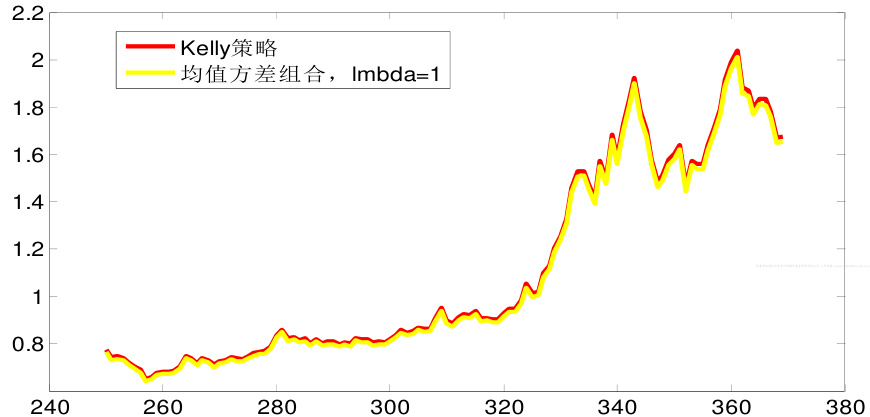
- 进一步比较Kelly策略与经典均值-方差组合，得出当风险厌恶系数（λ）为1时，拟合近似相等，表明Kelly策略是均值方差理论在特定条件下的推广；

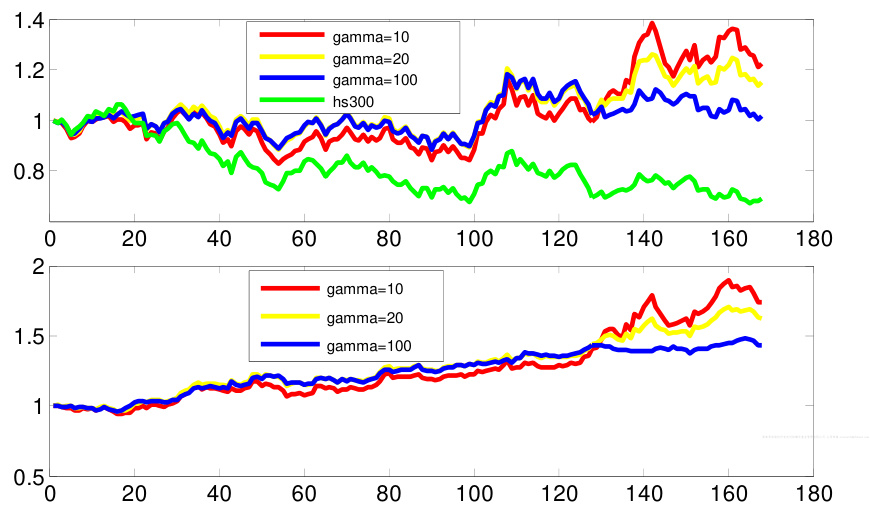
• 报告提出Fractional Kelly策略作为改良版本，引入γ参数调整对波动的惩罚力度，图表显示不同γ值对应组合表现保持稳健，且波动-最大回撤明显下降，适合更加保守的投资者。[page::14,15,16]

2.6 Kelly策略总结与风险提示（第17至18页）

• Kelly策略能有效提升长期收益，适合高波动市场及资产；

- 其主要短板是对波动性和回撤惩罚不足，实际应结合分数Kelly策略或选用高波动资产以规避体系缺陷；

• 实施需注意长期视角与收益周期，短期效果可能与均值方差组合无异；

- 报告明示了风险提示及免责声明，强调数据来源合规、报告观点独立、市场不确定因素和投资风险，提醒投资者谨慎决策。

• 权益归属明确，强调版权，提示投资者关注投资风险及专业建议。[page::17,18]

---

三、图表深度解读

以下是报告内主要表格与图表的详细分析：

3.1 贝努利分布部分（第6-8页）

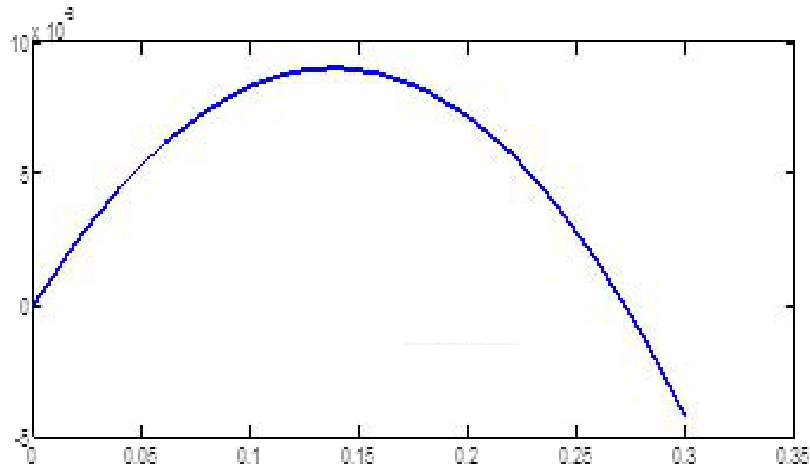
• 图表展示贝努利分布Kelly投资比例与对应预期几何增长函数关系：曲线呈现典型的凸性形状，存在唯一最优f值（投资比例）使得预期增长最大化；

- 行业配置表：每一行业的统计指标（胜率、涨跌幅、Kelly比例、预期及实际几何增长率）细致列出，数据反映各行业多空概率及上涨幅度，计算出最优Kelly比例；

• 贝努利Kelly策略累计财富增长图（一级与二级行业）：Kelly策略均优于沪深300指数，累计财富显著提升（达1.38和1.55）；

- 风险收益指标统计：胜率均高于70%，年化波动率较沪深300约2倍，最大回撤受控在5%-9%之间，显示风险控制良好。

3.2 对数正态分布Kelly策略部分（第9至13页）

• 理论计算公式推导图示、线性代数表达清晰，展示组合权重计算逻辑及几何增长关系；

- 一级、二级行业策略收益曲线显示Kelly策略策略曲线显著抬升与沪深300指数的差异，累计超额收益逐步放大；

• 风险收益表格显示财富终值和夏普比率大幅提升，和贝努利模型相比有更高的收益与波动；

- MVP方案比较图清晰展示两种模型的收益-方差权衡关系，Kelly策略位于更高的收益位置，支持理论优势。

3.3 无分布假设Kelly策略及Fractional Kelly改良模型（第14至16页）

• 无分布Kelly策略累计财富曲线与沪深300相比优势明显，收益稳定增长；

- 与均值方差理论重合情况图显示在λ=1时的均值方差组合与Kelly策略曲线高度重合，验证理论推导准确；

• Fractional Kelly策略表现对比图表列示不同γ参数值下组合表现，伴随γ增大，波动率和回撤下降，收益适度降低，说明对波动性的风险惩罚更加显著；

- 风险收益指标统计表明，分数Kelly策略在控制最大回撤（5%-12%）同时仍保持较好年化收益（11%-18%），夏普比率在1左右，适合风险偏好不同的投资者。

---

四、估值分析

本报告虽然主要为策略应用及理论分析，但间接涉及Kelly模型作为投资组合优化工具的估值思路：

• 采用的估值方法是基于Kelly公式的几何增长最大化，即通过估计投资组合长期复利增长率，来“估值”最优投资权重；

- 输入包括资产的胜率、盈亏比、均值收益向量、方差协方差矩阵等；

• 对应的优化问题为凸二次规划，约束条件为权重和为1；

- 通过敏感性调整（如Fractional Kelly引入风险偏好系数γ），可动态调节风险收益权衡，当γ=1时等价于原Kelly策略，γ>1时增加对波动的惩罚；

• 估值结果以最大财富终值及风险指标（回撤、VaR、ES）体现。

- 报告未直接提供传统的P/E、DCF等估值指标，但通过回测收益率与风险指标提供了策略有效性评估。

---

五、风险因素评估

• 波动风险不足：Kelly策略在数学上只对波动有部分惩罚，无法充分控制投资组合的极端下行风险，造成回撤较大；

- 胜率和盈亏比估计误差：策略基于历史概率估计，未来若参数显著偏离，投资比例计算将失准，影响收益和风险；

• 市场波动加剧风险：Kelly策略对高波动资产较为敏感，若波动异常放大，未加调节的Kelly策略可能导致资本迅速缩水；

- 假设限制风险：贝努利和对数正态假定可能不完全符合真实资产收益分布，尤其尾部风险以及市场联动效应未完全捕捉；

• 回撤风险：报告显示最大回撤在20%以上，适合风险承受能力强的投资者，短期波动可能导致资金压力；

- 流动性风险及实际操作风险：报告未深入涉及，但在现实中组合再平衡成本及市场摩擦亦可能影响策略表现。

缓解措施包括采用分数Kelly法降低仓位比例，加入波动性控制机制，或选择流动性较优且波动适中的资产以匹配Kelly策略结构。[page::1,17]

---

六、批判视角与细微差别

• 缺乏对模型参数不确定性的敏感性分析，例如胜率和盈亏比在市场环境剧变时变动对Kelly比例的影响未展开深入讨论；

- 策略适用范围强调为“长期”且收益率较高的资产，故短期波动或低收益资产可能表现平平，存在在实际较波动市场中的执行风险；

• 对侧重几何增长率的关注意味着对“潜在极端损失和投资者行为心理因素”的不足考量，这在投资组合理论中是重要层面；

- 报告中对Kelly策略与市场传统模型如均值方差的对比力量较大，但未重点讨论组合的多元化和风险因子对冲等现代量化策略中核心内容的融合可能；

• 部分公式文本的表达较为技术化，部分推导公式中符号排版略显混乱，可能导致理解门槛提升；

- 某些统计指标如VaR、ES未系统解释计算方法及置信水平，建议增加注释。

总体，报告内容严谨，数据详实，但对Kelly策略应用风险与现实操作难度的警示尚可加强，以避免读者对其策略完美性的过度误读。[page::5,17]

---

七、结论性综合

本报告系统全面地阐述了Kelly公式在行业配置策略中的理论基础、优化推导及实证表现，涵盖三种典型收益分布设定——贝努利、对数正态和无分布假设，分别建立了对应的策略模型。

关键发现包括：

• Kelly策略强调资本几何增长率最大化原则，理论上能实现投资组合的长期财富增长最优；

- 各分布假设下，Kelly策略均在中国A股一级和二级行业实现了明显优于沪深300指数的长期收益，尤其在对数正态及无分布模型中财富终值提升至2.3倍以上，年化收益超过50%；

• 相较传统的最小方差组合（MVP），Kelly策略显示出更高的收益潜力，但伴随着更高的波动和回撤，夏普比率也普遍更优；

- Kelly策略本质上等同于期望对数效用最大化，在短期波动较小时，表现类似风险厌恶系数为1的均值方差组合法；

• 最大缺陷为对波动惩罚不足，现实应用中通过分数Kelly策略(Fractional Kelly)进行风险调整有良好效果，兼顾收益与稳定性；

- 适合长期视角、收益率较高及具备一定风险承受能力的投资者和量化投资团队。

图表验证了上述结论：

• 贝努利模型下各行业Kelly比例细致解析，显示医药、家电等配置比例较高且回报理想；

- 累计财富曲线与超额收益图表直观展示Kelly策略在绝大多数时点持续跑赢基准；

• 对比MVP组合的收益风险表现，明确凯利组合更优，但风险管理不可忽视；

- 分数Kelly调整策略有效降低最大回撤和下行风险，风险收益权衡更合理。

总体而言，刘富兵先生的报告向投资者传递了Kelly策略在行业配置中的潜在价值，并针对应用局限提出了改良建议，促进投资者理性看待与实践该策略，是一份理论与实务兼备的高质量量化投资研究成果。[page::1-17]

---

图片溯源展示

• 报告封面页及联系信息（页0）

• 投资要点与Kelly策略概述（页1）

• 贝努利分布投资比例与收益函数关系图（页6）

• 贝努利分布下一级行业财富增长及统计（页8）

• 贝努利分布下二级行业财富增长及统计（页8）

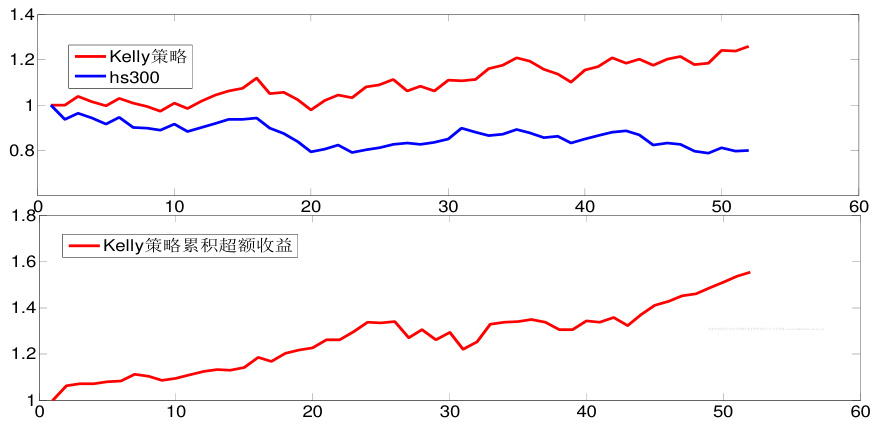
• 对数正态分布Kelly与MVP比较图（页11）

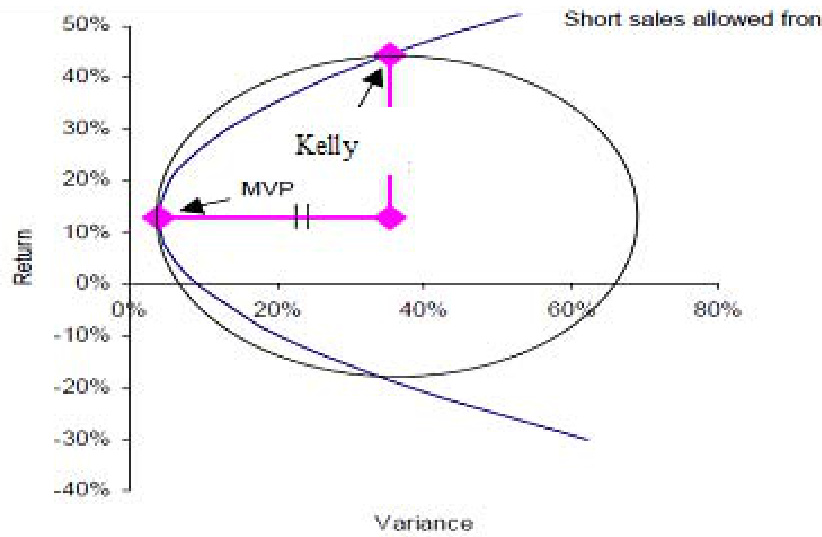
• 对数正态分布一级行业Kelly策略累计收益（页12）

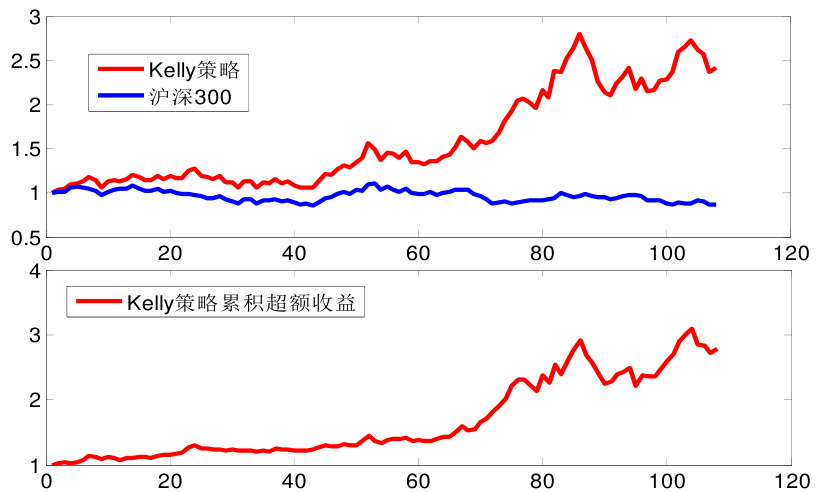
• Kelly与MVP累计超额收益对比（页13）

• 无分布假设Kelly策略收益表现（页15）

• Kelly与均值方差理论拟合图（页15）

• Fractional Kelly策略不同γ值表现（页16）

---

综上，国泰君安本次投资策略报告，既有理论系统性，也有实际策略回测佐证，对Kelly策略在行业配置的应用提供了宝贵参考。投资者应结合自身风险承受能力和市场环境理性应用该策略，方能发挥其长期超额收益优势。[page::0-17]

报告