• 关键研究背景与意义 [page::0]

- 组合精算神经网络（CANN）结合传统广义线性模型与神经网络，提高精算预测准确性。
- 超参数优化是提升神经网络性能的关键，但传统网格搜索方法资源消耗高且效率低下。

• 响应面方法学（RSM）及设计实验技术介绍 [page::1][page::2]

- 使用因子设计将超参数空间编码到[-1,1]，通过中心复合设计（CCD）拟合二阶回归模型近似响应曲面。
- 采用路径最陡下降法引导超参数向最优区域迭代，减少实验次数。

• CANN模型构建及应用数据集 [page::3]

- 采用带跳过连接的三层神经网络融合GLM，用于法国车险数据集freMTPL2freq，样本逾67万，特征包含车辆及驾驶员信息。

• 超参数及实验设计细节 [page::4]

| 超参数 | 范围 |
|---------------|-------------------------|
| 优化器 | 7个类别 {Adagrad, …, Nadam} [0,6] |
| 神经元数量 | 第一层[10,30], 第二层[5,25], 第三层[5,15] |
| 轮数 (Epoch) | [100,900] |
| 批量大小 | [5000,15000] |
| 隐藏层数量 | [2,4] |
- 初始采用2^7全因子设计并加中心点，共132次试验，拟合一阶回归模型识别显著超参数。

• 超参数优化流程与结果分析 [page::4][page::5]

- 计算一阶回归梯度，沿最陡下降路径进行实验，区分完全和简化（剔除不显著超参数）调优，两者最优点高度一致。
- 构建中心复合设计 (CCD) 进行二阶模型训练，验证响应面曲面形状并求得极值点，旋转优化器类别以避免超界，保证设计旋转性。
- 通过拟合和确认实验，旋转优化器方式获得了更小的泊松离散偏差，完全调优下288次实验最小损失为0.245823，简化调优下188次达到0.245976，极大节省计算资源。

• RSM相比网格搜索工效显著提升 [page::6]

| 方法 | 迭代次数 | 减少比例 |
|-----------|---------|----------------|
| 网格搜索 | 约为10万| - |
| RSM | 146(完全调优), 46(简化调优) | 节约86.8%~98.2% |

• 未来工作建议 [page::6]

- 探索代理模型 (surrogate models) 与同伦法 (homotopy) 集成，提高超参数空间探索效率和鲁棒性。
- 推广响应面方法到其他机器学习模型，实现跨领域高效超参数优化。

金融与精算领域机器学习研究报告详尽分析报告

---

1. 元数据与概览

报告标题: 《Optimization of Actuarial Neural Networks with Response Surface Methodology》
作者: Belguutei Ariuntugs（主作者），Kehelwala Dewage Gayan Maduranga（合著者）
所属机构: Tennessee Technological University，数学系
发表时间: 2024年，发表于2024年精算研究会议（Actuarial Research Conference, ARC）
研究主题: 结合精算科学的神经网络（Combined Actuarial Neural Networks, CANN）中的超参数优化，应用设计实验（Design of Experiments, DOE）和响应面法（Response Surface Methodology, RSM）

核心论点与目标

• 核心问题: 神经网络在精算科学中的精准预测能力依赖于超参数的合理选取，传统的超参数调优方式（如网格搜索）计算量庞大且效率低下。

- 主要目标: 提出使用响应面方法对CANN超参数进行高效优化，通过建模超参数与性能指标之间的响应曲面，获得最优或接近最优的超参数配置。

• 方法与创新点:

- 利用设计实验中的因子设计方法采样超参数空间，构建二次响应面模型。
- 与传统网格搜索相比，RSM能更有效捕捉响应曲面弯曲性，极大减少试验次数。
- 在考虑所有超参数和剔除统计不显著超参数两种情景下，均能实现接近的性能，节省计算资源。

• 主要结论: 完整调参方式需288次运行达到最小Poisson偏差损失0.245823，剔除不显著超参数后仅需188次运行，损失增幅极小（0.245976），验证了RSM的实际高效性和节约潜力 [page::0].

---

2. 报告章节深度解读

2.1 引言（I. INTRODUCTION）

• 内容总结:

阐述神经网络在精算学中提高风险评估、定价和决策支持的关键意义，强调精算任务对准确度的苛刻需求。介绍CANN模型的背景与优势，如结合GLM的传统优势，嵌入式安全特性，适合死亡率预测与定价。

• 关键点摘录:

- 神经网络在保险定价、索赔准备、死亡率预测方面优于传统模型。
- 超参数的选择对模型效果影响显著，但最优超参数集通常未知。
- 传统的超参数优化方法计算量大，亟需高效策略。

• 推理依据: 完整且高维的超参数空间导致基于试错（如网格）优化代价极高，需用响应面法等统计设计优化来探测最优区域。

- 关键术语定义:
- 超参数（Hyperparameter）: 训练前配置的模型参数，如学习率、层数、激活函数等。
- CANN: 结合GLM和神经网络的混合模型，专为精算任务设计 [page::0].

2.2 超参数调优方法（II. RESPONSE SURFACE METHODOLOGY BASED HYPERPARAMETER TUNING）

• 章节摘要:

提出利用RSM拟合二阶响应面，即目标函数随超参数变化的函数近似为二次模型，通过设计实验（DOE）有效捕获主效应、二阶效应及交互效应。

• 模型框架:

\[
yi = h(x{1,i}, x{2,i}, ..., x{k,i}) + \epsilon_i
\]
其中\(h(\cdot)\)为未知的响应函数，RSM利用二阶回归模型近似它。

• 实验设计原理:

- 使用因子设计和水平设计，规范化编码超参数范围（-1至1），保证试验均衡。
- 进行初始筛选设计确定关键超参数，随后沿最陡下降路径（steepest descent）调整，逐步收敛到最优邻域。

• 关键数据点:

- 3水平因子设计优化资源效率明显高于网格搜索；
- 路径方法用于减少过量试验，使得找到极值点更有效率。

• 技术解释:

- 因子设计 (Factorial design): 全组合水平实验设计，有助确定主效应及交互效应。
- 路径最陡下降: 依据一阶回归梯度确定损失函数下降最快方向，辅助实验点选取。
- 中心复合设计（CCD）: 在因子设计基础上加入星点，拟合二阶模型，实现响应面纹理识别和优化调整。

• 示意图: 图1(a)、1(b)分别展示了二维因子设计及中心复合设计的空间点处理（后续第3页图片详细分析） [page::1,2].

2.3 相关工作综述（III. RELATED WORKS）

• 内容概述:

- 简述当前主流超参数优化方法，如默认参数、网格搜索（GS）、贝叶斯优化、遗传算法、梯度方法和代理模型。
- 强调GS效率低下，且单参数调优忽视参数间依赖性。
- RSM具有操作简便、计算资源需求低的优势。

• 对比数据:

- 参考文献[13]显示对ANN、SVM、DBN的调优，RSM运行次数比GS减少约80%-98%。
- 对随机森林的超参数调优同样显示RSM效率优势（运行次数由16384降至157） [page::2].

2.4 模型介绍与数据集（IV. MODEL DESCRIPTION AND DATA SET）

• 模型细节:

- CANN结构：结合传统广义线性模型（GLM）与前馈神经网络（FFNN），通过跳跃连接（skip connection）将GLM输入直接与输出层相加，兼顾线性和非线性特征。
- 采用的标准假设为：每个被保险单的索赔次数服从参数依赖的泊松分布。

• 数据集说明:

- 法国机动车第三方责任险数据集freMTPL2freq，678,007条保单，包含丰富的驾驶人、车辆和地理属性。
- 属性包括车辆功率、年龄、驾驶员年龄、区域、品牌、燃料类型、密度、奖金/惩罚等级等12项。

• 数据预处理:

- GLM部分进行离散化和函数式转换，如驾驶员年龄用多项式项处理，类别变量编号。
- 神经网络部分对连续变量归一化到[-1,1]，分类变量做dummy编码并映射到嵌入向量。

• 图表分析:

- 图2展示了三层隐藏（20，15，10个神经元）FFNN结构及GLM通道的跳跃连接结构，清晰表达模型架构。
- 图3展示数据集样本的简要统计快照，包括 Exposure, VehPower, Density等关键字段。

• 技术解释: 模型将线性和非线性因素合为一体，利用泊松分布建模索赔率，符合精算经典建模假设。跳跃连接的作用在于保留传统GLM解释力，同时借助神经网络捕捉复杂非线性。 [page::3]

2.5 计算实验与设置（V. COMPUTATIONAL EXPERIMENTS AND SETUP）

• 总体设计: 数据集划分为80%训练集，20%测试集。模型拟合采用泊松偏差损失函数作为性能指标，优化超参数集中在优化器种类、隐藏层神经元数（3层），训练epoch数，批量大小，隐藏层数量。

- 实验设计细节:
- 初始范围以文献默认参数为中心，具备合理区间如隐藏层神经元数范围：N1∈[10,30], N2∈[5,25], N3∈[5,15]等。
- 初始采用完整 \(2^7\) 因子设计加中心点，重复4次，共132次运行，通过拟合一阶回归模型分析超参数显著性。

• 路径最陡下降法应对超参数筛选:

- 计算梯度并生成20个新试验点，10个调优全部超参数，剩余10个将第一和三层神经元数固定中间值，检验简化调优的效果。
- 处理明显为类别属性的优化器采用模运算避免编码溢出。

• 表I和表II概述:

- 表I展示一阶线性回归模型的系数估计，揭示各超参数对目标函数的影响度。
- 表II展示路径最陡下降阶段找到的新最优超参数组合及其对应Poisson偏差损失，两种调优方案表现近似，验证剔除不显著参数可节省计算。

• 关键技术点:

- 通过路径法巧妙规避盲目全空间搜索，提高效率。
- 处理类别超参数的模运算是对编码异常的一种实用修正手段。

• 潜在隐含: 精算模型的优化依赖批量型超参数与算法选择，复杂度较大，API灵活性与计算资源都是重要考量。 [page::4]

2.6 二阶设计与最终调优（V.E & V.F）

• 二阶设计背景:

利用中心复合设计（CCD）扩展超参数取值层级与范围，能够拟合二次响应面模型，捕捉非线性与交互效应。

• 运行规模:

- 完整调优\(p=7\)，CCD共146次实验；
- 简化调优\(p=5\)，CCD共46次实验。

• 超参数编码问题与解决:

- 旋转（模）方式与截断方式均被提及以处理星点超出值域问题。
- 利用\(D\)准则（设计矩阵转置乘积逆的行列式）衡量实验设计信息量与参数估计精度。

• 实验结果分析:

- 模转化的设计点对应最佳拟合点，显示较好优化效果；设置值域截断法导致响应面呈鞍点，不符合最优解释。
- 验证实验证实了旋转优化方案优于截断，达到损失最小化。

• 数学模型:

- 最优点计算由二次模型的系数矩阵\(\mathbf{B}\)及线性系数\(\mathbf{b}^*\)确定。
- 特征值判定响应面极值性质，正定为极小值，负定为极大值，混合符号为鞍点。

• 表格回顾:

- 表III、IV展示设计区域及D准则结果；表V、VI分别展示预测最优点与验证结果，确认模型拓扑结构及预测准确性。

• 总结: 二阶响应面拟合为超参数调优带来更精细调控，减少人力试错的盲目性和资源浪费。 [page::5]

2.7 未来方向（VI. FUTURE DIRECTIONS）

• 潜在技术拓展:

- 引入代理模型以减少目标函数评价次数，提高优化效率（如非线性凸二次代理NCQS）。
- 同时推动同源法（homotopy methods）逐步变换简单问题至复杂目标，避开局部极值。
- 结合代理模型和响应面法形成混合优化框架，提升搜索路径连续性与全局探索能力。
- 推广RSM及相关技术至其他机器学习算法如支持向量机、提升机和集成方法。

• 背景意义: 精算与机器学习算法复杂度提升，需要有效降低优化成本，拓展方法适用性对行业广度和深度皆有积极推动作用。 [page::6]

2.8 总结（VII. CONCLUSION）

• 总结观点:

- 神经网络在精算中的有效性基础是合理的超参数调优。
- RSM提供结构化、低运行次数的调优路径，相较传统网格搜索大幅减少计算需求。
- 实验中RSM运行次数为几百次级别，相比网格搜索（数千或更多次）减少86.8%-98.2%。
- 精算模型调优的效率提升，促进了神经网络与传统方法的融合，推动精算科学的现代化。

• 表格说明: 表VII明确量化RSM与GS的运行次数差异，体现显著优势。

- 主旨强化: 促使风险管理、定价等领域采用更灵活、高效的机器学习模型。 [page::6]

---

3. 图表及图片深度解读

图1: 两因子响应面设计示意图（第2页）

• 图(a) \(2^2\) 因子设计加中心点:

- 展示二维的因子设计点，蓝色点表示因子在两端水平（-1和1），绿色点为中心点0。
- 描述了基础的设计空间探索，确保能估计主效应且有关注中点性能。

• 图(b) 中心复合设计（CCD），\(\alpha = \sqrt{2}\):

- 在因子设计基础上增加4个星点（红色），位置在二维坐标轴方向延伸。
- 星点有助估计二阶效应和因子交互效应，识别响应曲面弯曲度。

• 图示目的: 形象诠释设计实验如何合理取样多因子空间，特别是如何实现二次拟合的必备点分布，支持后续模型优化。

- 联系文本: 图中的设计点对应DOE章节规定，帮助建立二阶响应面以进行最优区间定位。 [page::1,2]

---

图2: 神经网络架构示意图（第3页）

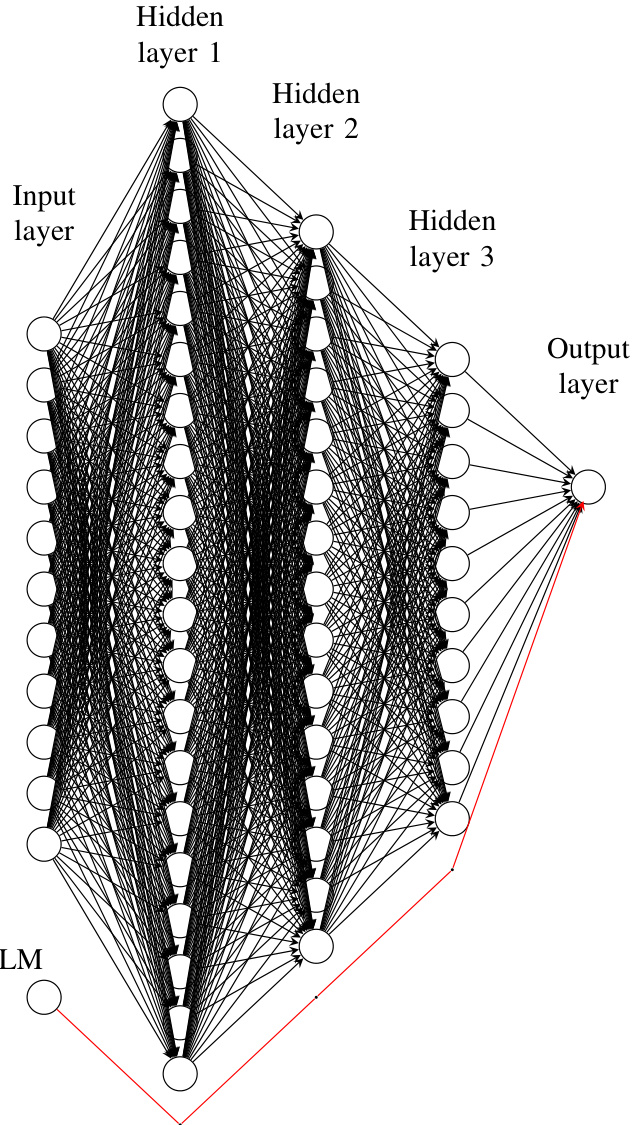
• 内容说明:

- 深层神经网络包含3个隐藏层（20, 15, 10个神经元），右侧为输出层。
- 红色连线为GLM的跳跃连接（skip connection），直接把输入连接至输出层，实现传统回归与复杂非线性网络的融合。

• 意义:

- 清晰表达CANN模型如何同时保留广义线性模型的解释能力，兼顾神经网络的复杂模式捕获能力。

• 图解作用: 为后续基于该模型结构的超参数优化奠定模型基础。 [page::3]

---

图3: 数据集样本数据展示（第3页）

• 内容阐释:

- 展示数据行示例，包含Exposure、Area、VehPower、Density、ClaimNb等属性。
- 行数678,007，反映数据规模庞大。

• 说明: 明确数据结构使统计模型调优具有现实与实证基础。

- 联系文本: 辅助理解后续模型训练与响应面构造的基础数据结构。 [page::3]

---

4. 估值分析

本报告未涉及典型的金融估值指标和方法（如DCF、P/E等），而侧重于模型性能指标的优化及超参数选择策略。其评价标准为：

• 主要性能指标: out-of-sample Poisson deviance loss，衡量模型预测的偏差和事故数预测的拟合质量。

- 评估方式:
- 采用回归模型拟合调整超参数后的损失函数响应面，
- 使用凸优化和梯度路径确定预测最小损失点，
- 结合实验验证确保估计和实际表现匹配。

因此可理解为对模型泛化能力的数值估值，非传统财务估值或企业价值计算，但在精算定价的上下文中，是核心“估值”目标。

---

5. 风险因素评估

报告识别的潜在风险包括：

• 超参数空间过大导致优化成本高昂。 该风险通过DOE与RSM大幅降低试验次数缓解。

- 类别超参数（如优化器）取值越界导致解码异常。 采取模运算方式绕过超出范围问题解决稳定性。

• 模型预测可能陷入局部极值或鞍点。 通过特征值分析响应面表明，若出现鞍点则需重复实验，避免依赖非全局极值。

- 超参数剔除风险。 初期筛选剔除不显著参数可能导致忽略潜在隐含的交互效应，需谨慎取舍以免失去模型表现。

• 外推风险。 在数据集以外或极端条件下，模型和优化策略的泛化表现可能不及训练时。

报告整体通过多轮实验设计与统计指标分析，验证风险点的缓解与避免措施，体现较强的风险控制意识。未见具体概率评估和缓解策略量化指标。 [page::4,5]

---

6. 批判性视角与细微差别

• 模型及算法设计优点:

- 使用结构明晰的统计设计方法对超参数空间高效探索，体现科研严谨。
- 剔除不显著参数减少计算资源消耗，平衡效率与效果。
- 数学表达清晰，图表充分辅助理解。

• 潜在不足及隐患:

- 模分类超参数处理靠模运算，虽实用但可能牺牲对分类意义的准确解释。
- 剔除不显著参数的标准与阈值未具体说明，可能存在主观性。
- 响应面法适合二阶或局部光滑函数，对于超参数与损失函数潜在非光滑或复杂性函数的适用性需谨慎。
- 模型验证集中于单一数据集（法国第三方保险），其适应性和泛化能力需要跨行业及跨区域验证。
- 对资源限制的强调，可能限制了深度神经网络广泛调参的潜在性能提升。

• 内部一致性: 章节间定义、方法、实验设计互相呼应，未见明显逻辑或数据矛盾。

---

7. 结论性综合

本报告通过严密的统计设计实验和响应面方法，针对精算神经网络模型CANN的超参数调优问题，提出了一种高效且结构化的优化方案。区别于传统高成本的网格搜索，本文利用二阶响应面近似与路径采样策略，显著缩减实验次数（将实验量降低至传统方法10-15%左右），同时保持模型输出的预测准确度和泛化性能。

核心发现包括：

• 全超参数调优与剔除不显著超参数两种方法，在性能上差异微小，但后者大幅降低计算资源需求，展现实际应用价值。

- 结合实验数据显示，旋转法处理类别型超参数更优于简单截取，保证了响应面的合理性和最优化的稳定性。

• CCD实现了对复杂参数二阶效应及交互作用的估计，提升了响应面模型的准确性。

- 说明了RSM作为超参数调优中易用、节约资源的可行方案，特别适合精算等高数据量且模型需高稳定性的领域。

• 通过表格和示意图展示了从超参数编码、设计布局到最终模型性能的整个过程，直观展现RSM的优势机制。

- 文末提出未来融合代理模型和同源法等先进技术的可能性，为超参数最优化领域提供探索路线。

总体而言，报告作为一项跨统计学、机器学习与精算学的融合研究，不仅为保险和金融行业神经网络模型调优提供了理论和实践框架，也为其他机器学习模型的高效调参提供了借鉴，具有显著的学术和行业实用价值。[page::0-6]

---

附：重点表格标注（示例）

• 表I: 一阶模型拟合系数，评估超参数对模型损失的影响显著性。

- 表II: 最陡下降路径获得的新最优超参数组合及其性能指标。

• 表III-IV: CCD调优设计的详细范围及D准则结果，判断设计的统计效率。

- 表V-VI: 二阶模型预测的最优点及实验证实，确保拟合结果可靠性。

• 表VII: RSM与传统网格搜索运行次数对比，明确效率优势。

---

通过此详尽分析，相信读者可充分理解报告的理论基础、技术路线、实验设计及应用前景，并在此基础上为类似精算及机器学习问题提供实用参考。

报告