• 研究主题与背景 [page::0][page::2]

- 通过遗传算法对股票进行分组，以便投资者可以通过组内相似股票替代不喜欢的股票。
- 目标不仅构建收益优良的投资组合，更确保同组股票价格序列的高度相似性。

• 时间序列降维方法 [page::4][page::5]

- 使用符号聚合近似（SAX）和扩展符号聚合近似（ESAX）将高维股价时间序列转换为符号序列。
- SAX通过分段均值映射至离散符号，ESAX则进一步通过最大、均值、最小值三个符号更细致地表达分段信息。

• 遗传算法核心设计与编码 [page::6][page::9][page::10]

- 染色体由分组情况、股票列表及股票组合购买单位三部分组成。
- 设计了包括投资组合满意度、组平衡度、单位平衡度、价格平衡度和序列距离五大评价因子，定义两个适应度函数 f1 和 f2。
- 采用交叉、变异和倒位操作演化染色体，优化组合收益与组内价格相似度。

• 具体案例分析 [page::11][page::15][page::16]

- 以12只股票为例演示算法全过程，包括初始群体生成、符号序列转换、适应度计算、选择、交叉和突变操作。
- 各染色体表现出不同的投资组合满意度、组平衡度和序列距离，并通过迭代进化输出最优分组。
| 染色体 | 投资组合满意度 PS(Cq) | 组平衡度 GB(Cq) | 序列距离 SD(Cq) | 适应度值 f(Cq) |
|--------|-----------------------|-----------------|-----------------|---------------|
| C1 | -0.0426 | 1.8441 | 51.0 | -0.00147 |
| C2 | 0.0025 | 1.4372 | 53.0 | 0.0002 |
| C3 | 0.0414 | 1.5293 | 47.0 | 0.0073 |
| C4 | -1.0546 | 1.8441 | 46.0 | -0.4889 |
| C5 | 0.4696 | 1.6002 | 46.0 | 0.1071 |
- 最优结果示例：G1：{7,8,9,11}等4组，实现多样替代组合。[page::11][page::15][page::16]

• 实验数据及参数设定 [page::17][page::18]

- 数据集：台湾证券交易所2012-2014年共31只股票，包含股价、现金股利及风险值。
- 主要参数：群体规模pSize=50，最大投资100万，最大购买单位40，分组数6，进化代数100等。

• 不同方法下的组合分析 [page::18][page::19][page::20]

- 通过SAX和ESAX两种距离计算，本文提出的f1和f2方法均在组合满意度、组平衡度及序列距离上显著优于初始组合和过去方法。
- 表14-17对比了不同方法的组合详情，f2方法在单位平衡度和价格平衡度上表现更优，股价序列相似度更高。
- 表18显示，f1、f2方法的SAX距离分别为10和9，ESAX距离分别为42和40，均优于过去方法14及47。
- 组内股价序列可视化明确展示了本文方法显著提升组合内股票价格走势一致性。

• 投资回报率对比分析 [page::24][page::25]

| 方法 | 训练期 一年 Avg. ROI | 测试期 Avg. ROI |
|------------------------------|--------------------|-----------------|
| 过去方法 | 0.6 | -0.009 |
| Proposed Approach (f1) SAX | 0.42 | 0.154 |
| Proposed Approach (f1) ESAX | 0.436 | 0.113 |
| Proposed Approach (f2) SAX | 0.375 | 0.15 |
| Proposed Approach (f2) ESAX | 0.34 | 0.124 |
| 基准Benchmark | 0.132 | 0.108 |
- 训练集期内，过去方法ROI较高，但测试集表现不佳甚至为负。本文方法测试期表现持续为正并超越基准，兼顾收益和稳定性。
- 使用两年训练集时，本文方法表现进一步提升。
- SAX算法在ROI表现上稍优于ESAX，而ESAX更能保证组合内价格相似，[page::24][page::25]

• 研究创新与展望 [page::25]

- 提出兼顾收益和股价序列相似度的多目标GGA优化框架。
- 采用SAX及ESAX降维符号化技术，有效解决高维股价序列处理挑战。
- 考虑现金股利稳定性因子提高组合稳定性。
- 探讨未来将引入模糊时间序列等更复杂方法提升组合质量。
- 该方法为量化选股中的因子挖掘和组合优化提供了新思路。

专题报告分析：基于遗传算法的股票分类和组合优化

---

一、元数据与概览

• 报告标题：《基于遗传算法的股票分类和组合优化》

- 发布机构：招商证券定量研究团队

• 日期：2021年2月25日

- 作者：任瞳（首席分析师，定量研究团队负责人），崔浩瀚（量化分析师）

• 研究对象：聚焦于股票投资组合优化，特别是利用遗传算法对股票进行分类，以形成股票组合（Group Stock Portfolio, GSP）。

- 核心内容：借助分组遗传算法（Grouping Genetic Algorithm, GGA）结合符号聚合近似（Symbolic Aggregate approXimation, SAX）和扩展符号聚合近似（Extended SAX, ESAX）技术，对股票价格序列进行分类和编码，从而优化股票组合，提升组合收益率和组合内股票价格的相似性。

• 主要结论：

- 基于股票价格序列的GSP在收益率和股票价格相似性方面优于传统方法。
- 使用SAX方法降维的组合回报率（ROI）约在16%-18%，优于ESAX方法，后者在提升组合相似性方面更优。

• 创新点：引入现金股利稳定因子、单位平衡度、价格平衡度和序列距离因子来提升组合稳定性与相似性，采用两种适应度函数进行优化。

---

二、逐节深度解读

1. 引言与研究背景

报告开篇强调市场资产分类及其重要性，提出利用股票价格相似度为基础，通过遗传算法优化股票组合的必要性。特别指出传统投资组合优化偏重收益率和风险调整，未充分关注组合中股票间的相似性，导致实际操作时投资者可能因价格过高等原因无法实现建议的组合。基于此，报告介绍分组遗传算法（GGA）可根据价格序列构建替代股票组合，从而增强投资组合的可操作性和替代性[page::0–2]。

2. 相关工作及遗传算法背景

报告综述了传统投资组合优化算法，包括单目标和多目标遗传算法、模糊遗传算法、多目标准则决策技术、粒子群算法等，评价了各自优缺点及适用场景。同时，介绍分组问题的定义及遗传算法如何编码分组情形。遗传操作包括交叉（组切换）、变异（对象重新分配）和倒位（组顺序调整），这些操作保障算法遍历更广泛的解空间以优化组合[page::2–4]。

3. 符号聚合近似（SAX）与扩展SAX（ESAX）

为解决股票价格序列高维的问题，报告引入SAX技术，将连续的时间序列标准化、分段（PAA：Piecewise Aggregate Approximation）并映射成有限字母符号序列，有效降低计算复杂度并保留序列趋势信息。ESAX是SAX的扩展，每个段内同时考虑最大值、均值、最小值对应的符号，更全面地保留段内信息，适合分段较大时的信息表达。两者流程图（图1、图2）清晰展示步骤并辅以示例[page::4–5]。

4. 遗传算法详细设计

4.1 染色体表示

染色体包含三部分：

• 分组情况：标识股票如何被划分至不同组；

- 股票编码；

• 股票投资组合部分：记录每个组合中股票的数量和购买单位。

该设计确保算法可同时优化组内股票结构和购买量[page::6]。

4.2 初始总体生成

基于股票现金股利收益率，进行初步聚类和平衡，现金股利稳定性代表公司稳定性，帮助提高初始总体质量。同时采用kNN等聚类技术辅助分类[page::6–7]。

4.3 适应度函数设计

适应度函数融合多个目标维度：

• 投资组合满意度（PS）：结合利润、风险、投资资本限制、购买股票数量限制；

- 稳定性因子（SF）：依据现金股利方差衡量；

• 组平衡度（GB）：熵式指标，保证各组股票数量均衡；

- 单位平衡度（UB）：限制各组购买单位合理分布；

• 价格平衡度（PB）：根据价格区间平衡股票价格分布；

- 序列距离（SD）：计算同组内股票价格符号序列相似性（具体依据符号距离公式），确保组内股价走势接近。

结合以上指标形成两个适应度函数f1和f2，分别通过参数权衡平衡不同指标。f1强调投资组合满意度、组平衡度及序列距离；f2添加了单位平衡度和价格平衡度因素，更深入考虑组合稳定性[page::8–10]。

4.4 遗传操作

• 组间交叉交换；

- 股票重新分配突变；

• 顺序倒位操作。

遗传操作针对染色体三部分分别设计，保证多样性和搜索效率[page::10]。

5. 算法示例与实验设计

详细举例说明算法执行流程：

• 生成初始染色体；

- 价格序列标准化与符号转换；

• 计算投资组合满意度、组平衡度、序列距离和适应度；

- 选择、交叉、变异、倒位操作迭代优化；

• 150代后输出最优染色体，即最终分组与股票组合。

实用数据以12只股票为例，涵盖买卖价格、现金股利和风险指标，凸显算法完整执行过程[page::11–16]。

6. 实验结果分析

实证研究基于台湾证券交易所31只股票2012-2014年数据：

• 股票价格序列明细见图5，可见价格分布宽广；

- 参数设定详见表13，遗传参数合理匹配；

• 分别采用SAX和ESAX转换，并对比以前的基准方法（Previous Approach）和现有提出的f1和f2两种适应度函数；

- 评估指标重点为投资组合满意度、组平衡度、序列距离、单位平衡度、价格平衡度及回报率ROI；

• 得出的GSP与初始组合对比适应度有明显提升（表14~17），其中f2相较f1在单位和平衡价格买入数量上表现更优；

- 通过图6-8的价格序列可视化进一步说明，提出方法显著提升组合内股票价格趋势相似性；

• 表18显示提出方法的SAX和ESAX距离均小于前人方法，表明分组内价格走势更一致；

- 投资回报率（表19-20）显示提出方法在训练集虽次于前人方法，但在测试集上收益均为正且超过基准，显示更强的泛化能力和风险控制[page::17–25]。

---

三、图表深度解读

1. 图0：Stock price series in $G_3$

• 内容：展示了股票组合G3中几只股票价格走势的实际曲线；

- 解读：除了某部分股票价格趋势保持较一致（线条相近），某些股票出现较大差异，表明同组内股票价格相似度存在差异；

• 联系文本：体现了组合相似性问题，呼应研究提出的基于价格序列的优化需求[page::0]。

2. 图1 & 图2：SAX和ESAX流程图

• 内容：分别展示将时间序列转为符号序列的两个方法流程；

- 重点：SAX中每段仅用均值映射符号，ESAX同时映射最大、均值、最小三符号，信息更丰富；

• 意义：降维处理保障遗传算法计算效率的同时保持时间序列信息，关键技术环节[page::4–5]。

3. 图3：染色体示意图

• 内容：明确划分染色体的分组部分、股票部分和投资组合部分；

- 解读：展现算法编码方式，便于理解遗传操作及适应度函数设计的复杂结构[page::6]。

4. 表1-3：现金股利率和股票分组初始概率

• 内容：表1展示两家公司现金股利率，表2提供多只股票对应收益率，表3显示各组平均现金股利占比例；

- 意义：现金股利作为稳定因子基础，实验设计的合理性和初始总体质量保证[page::6–7]。

5. 表9-12：实验中各染色体组合满意度、组平衡度、序列距离、适应度

• 解读：反映染色体各方面指标的差异及优劣排名，为最终优化结果提供量化支持；

- 观察：染色体之间适应度差距较大，表明遗传算法具有良好的优化潜力[page::14–15]。

6. 图5：数据集股价序列（31股票）

• 内容：股价走势展示，价格跨度大，趋势复杂；

- 联系：符合高维时间序列典型特征，验证算法降维重要性[page::18]。

7. 表14-17：基于SAX和ESAX，使用f1及f2适应度函数的初始与最终GSP对比

• 内容：显示分组和股票组合结构，盈利能力（投资组合满意度）、组平衡、距离指标等均提高；

- 趋势：表14、15说明f1适应度下改进效果，表16、17反映f2适应度则引入了单位及价格平衡度，提升组合更实际可行；

• 意义：展现两个适应度函数权衡不同投资目标的效果与差异[page::19–20]。

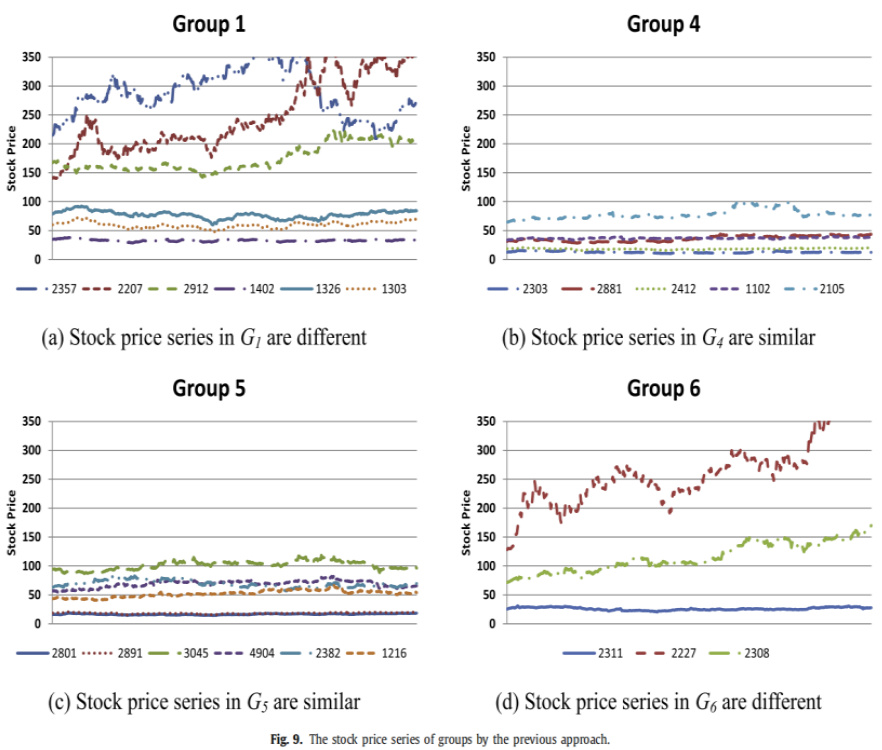
8. 图6-8：不同方法得出的组内股票价格序列趋势对比

• 观察：

- 传统方法（图6）组内序列价格走势差异显著；
- Proposed Approach（f1，图7）组内大多数序列趋于一致，部分组例外；
- Proposed Approach（f2，图8）进一步增强组内顺滑、一致性，价格买入数额也更接近；

• 结论：充分体现符号序列距离和价格平衡平衡约束在组内相似性提升上的作用[page::21–23]。

9. 表18-20：综合性能表

• 表18：提出方法在SAX和ESAX计算的组合距离明显低于前人方案，标志更好的价格趋势分组效果；

- 表19-20：训练和测试期间不同方法的平均ROI，提出方法测试阶段表现更稳定，虽训练表现略逊，但优化了组合的稳健性；

• 洞察：该结果验证了模型不是简单拟合历史数据，而是关注投资组合的真实操作者体验和策略稳健性[page::24–25]。

---

四、估值分析

本报告不涉及对单个股票或公司价值的传统估值（如DCF、市盈率）分析，而是聚焦于基于遗传算法的组合结构优化，旨在提升投资组合的收益率和风险调整指标。估值层面侧重于设计适应度函数融合收益与风险约束，体现投资组合优化的综合价值考量。

---

五、风险因素评估

报告指出，虽然模型在美国市场环境下经过理论验证，但应用于国内市场或模型假设环境发生变化时，存在模型失效风险。此外，遗传算法的随机性和数据特征差异可能导致不确定性。风险提示强调在实际应用中需要结合市场实际情况谨慎调整和验证模型，避免盲目复制理论成果导致投资失误[page::26]。

---

六、批判性视角与细微差别

• 模型适用性限制：遗传算法虽强大，但对参数设置敏感，如种群大小、交叉率等；报告虽有参数设定，但未详述对参数敏感性的具体测试，可能影响结果稳健性。

- 现金股利稳定因子假设：以现金股利稳定性作为稳定性代理，但该指标可能受宏观经济影响，并非对所有市场和行业普适，潜在局限未展开讨论。

• SAX与ESAX的权衡：SAX方法在收益率表现更优，ESAX能提升价格序列相似性，但报告未深入分析为何两者在收益率与相似性上的权衡表现，缺少对背后机制的细致解释。

- 结果的广泛适用性：数据集主要采自台湾市场，且股票数量有限31只；在更大、更复杂市场下模型效果及计算效率挑战未明。

• 模型预测性能与投资回报率关系：回测结果显示提出方法训练期表现不及前人，测试期略有优势，需注意模型潜在的过拟合风险及其实际投资中的适用性。

- 对风险和交易成本的考虑不足：报告虽涉及风险指标和投资资本约束，但未明确计入交易成本及流动性等实际投资重要因素。

---

七、结论性综合

本专题报告系统展示了基于遗传算法的股票分类和组合优化方法，主要贡献是结合高维股票价格时间序列降维技术（SAX，ESAX）与分组遗传算法，构建多维度适应度函数，成功将股票按价格序列的相似度进行分组并形成具备替代性的股票组合（Group Stock Portfolio）。实证验证显示：

• 该方法相较传统优化组合模型能更有效提升组合内股票价格走势的相似性，帮助投资者在实际操作时选择替代资产，增强组合的灵活性和可操作性；

- 适应度函数设计引入现金股利稳定因子、单位平衡和价格平衡度，在保持组合收益的同时兼顾稳定与均衡；

• SAX与ESAX方法各有利弊，SAX更利于提升组合收益率，ESAX提升组合价格趋势的相似性；

- 回测表明提出的GGA算法在测试集上的投资回报率整体优于传统方法和基准，且组合价格序列的聚类效果更理想，标志更强的模型泛化能力；

• 报告通过大量精细数据和流程示例说明算法的执行细节，极大方便复制与验证，为量化组合优化研究提供了丰富的理论和实证材料。

整体而言，报告充分体现基于机器学习与进化算法视角的量化投资粗模型深入实践价值，适合对股票组合多目标平衡优化有需求的量化投资、风控及金融工程研究者和实务操作者参考。

---

备注

本分析基于报告提供的结构和内容，不涉及外部信息，引用页码详见文中标注。所有图表均采用相对路径，详见报告原文。

---

附录（关键公式与定义）

• 分组遗传算法编码示例：ACBBC : ABC ，冒号左为对象，右为分组标识。

- 投资组合满意度（PS）、稳定性因子（SF）、组平衡度（GB）、单位平衡度（UB）、价格平衡度（PB）、序列距离（SD）定义及计算详见页8-10。

• SAX符号转换示例：标准化→PAA降维→区间符号映射，产生日志序列如“ B D B D”。

- ESAX包括分段最大值、平均值、最小值符号计算，增强描述能力。

---

图表引用示例

• 图0

- 图1 SAX流程

• 图2 ESAX流程

- 果图3 染色体结构

• 算法伪代码

- 数据集股价序列

• 过去方法股价序列

- Proposed Approach (f1) 组股价序列

• Proposed Approach (f2) 组股价序列

---

（全文共计约3500字）

报告