• 逆向欧式期权在加密资产市场的重要性：

- 定价以加密货币结算的期权（如 Deribit 交易所上主流的 Inverse options）需要特殊定价技术，因其标的和结算货币均为加密货币，且市场结构与传统资产不同 [page::1].

• 理论核心：基于 Malliavin 微积分，借助预期 Itˆo 公式，给出逆向期权平值隐含波动率（ATMIV）和隐含波动率偏度的短期期限渐近公式 [page::3][page::7][page::9][page::10].

- 主要假设体系：
- 资产价格服从特殊随机波动率模型，假设波动率过程 $\sigmat$ 满足一系列光滑性、界限性和 Malliavin 可微条件（见假设1-4）[page::3][page::4].

• 关键结果（Theorem 1）：

- 短期极限隐含波动率 ATMIV水平趋近于初始波动率 $\sigma0$；
- ATMIV偏度依赖于 Hurst 指数 $H$，当$H<1/2$时偏度以$T^{H-1/2}$尺度爆炸，需做相应尺度修正，可表达为积分 Malliavin 导数的函数，且依赖于基础资产-波动率相关系数 $\rho$[page::5][page::12][page::13].

• 数值验证：

- SABR模型中，波动率偏度收敛于 $\frac{1}{2}\rho\alpha$，数值模拟结果与理论吻合良好，$\rho$ 的符号决定偏度符号，$\alpha$ 为波动率之波动（vol-of-vol）[page::14][page::15].
- 分数 Bergomi 模型引入 Hurst 指数 $H$，粗波动（$H<0.5$）导致偏度爆炸，需乘以$T^{\frac{1}{2}-H}$，同时偏度表现出明显的幂律型态；数值回测验证与理论预期一致[page::16][page::17][page::18].

• 实证应用：

- 以2024年5月7日Deribit日内比特币期权市场数据为样本，利用最短期（1日）期权拟合隐含波动率，估计市场初始波动率约为0.36；
- 通过拟合市场隐含波动率偏度的幂律函数，估计 Hurst 指数约为0.8，表明市场波动率具有较平滑的结构，且 SABR 模型无法准确拟合此幂律偏度行为[page::18][page::19].

• 量化策略相关内容缺失，报告主要聚焦在随机波动率模型隐含波动率的理论建模与数值实证分析。

详尽分析报告：《On the implied volatility of Inverse options under stochastic volatility models》

---

一、元数据与概览

• 标题：On the implied volatility of Inverse options under stochastic volatility models

- 作者：Elisa Alòs, Eulalia Nualart, Makar Pravosud

• 发布机构及日期：未明确，但文章定位为学术研究论文，时间为2025年4月15日

- 研究主题：研究基于随机波动率模型下，逆向欧式期权（Inverse European options）隐含波动率特性，重点在短到期期权的隐含波动率及其偏斜（skew）特性，应用于加密货币期权（尤其是比特币）。

• 核心论点与目标：

- 通过Malliavin微积分方法（尤其是预期Ito公式）推导逆向期权的隐含波动率在期权到期时间趋近零时的极限表达式，以及这一隐含波动率的偏斜短期渐近公式。
- 该偏斜与波动率模型的「roughness」（粗糙度，即Hurst指数$H$）紧密联系。
- 结果形式可推广至Quanto-Inverse期权。
- 应用到经典SABR模型、分数量Bergomi粗糙波动率模型，并提供相关数值模拟验证。
- 最后，以Deribit交易所比特币期权实证数据验证理论结果的有效性。

• 创新点：

- 首次为逆向欧式期权隐含波动率提供严谨的短期渐近分析。
- 针对非经典黑–舒尔斯公式非单调性的问题，针对小到期时的反函数进行深入研究。
- 将粗糙波动率模型的Hurst指数对偏斜行为的影响明确量化。

---

二、逐节深度解读

1. 引言（Section 1）

• 要点总结：介绍加密资产衍生品兴起背景，解释为何加密货币资产的分类（证券、货币或商品）影响定价方法，指出加密资产（如比特币）不符合传统证券和法币的定义，同时也不完全可归类为普通商品。

- 推理与论证：通过考察加密资产去中心化、非法币流通性和极端波动性，排除了证券和法币身份；又基于成本、存储、供应控制及内在价值的分类标准，尚难将其定性为商品；引用文献[1,10,12,15,17,20]支持观点。

• 关键数据/论点：加密货币的极端波动性及缺乏稳定储值功能使其在实务上更适合用逆向期权定价。

- 结论：由于衍生品市场尤其Deribit交易所上的逆向欧式期权占主导，研究这一期权的定价模型及隐含波动率特征至关重要。

2. 逆向欧式期权及其市场（Section 1 & 2 引申）

• 要点总结：定义逆向欧式看涨期权，其回报以加密货币（而非法币）结算；阐述Deribit交易所逆向期权市场份额及其流动性优势。

- 推理：相较于外汇期权模型，逆向期权允许以加密货币为单位交易，更符合加密资产的交易场景，理论模型需与轨道不同。

• 核心公式：逆向期权的回报为$\left(\frac{ST - K}{ST}\right)+$，关注点在于以$ST$（美元定价下的比特币价格）为基础，计算利得。

- 实务关联：变现方式及保证金机制（加密货币保证金而非法币）带来定价和风险控制的特殊性。

3. 数学模型与基本假设（Section 2）

• 模型框架：

- 资产价格动态服从随机波动率模型
- $dSt = \sigmat St dWt$，$Wt$为带相关性的布朗运动组合
- 假设1-4（关于波动率过程$\sigmat$的适应性、连续性及Malliavin可微性，尤其涵盖粗糙度指数$H$性质）

• 关键推理：

- 模型不包含无风险利率（设为零），与文献[5]一致，简化分析。
- 波动率不作为交易资产存在，确保无套利和风险中性测度$\mathbb{P}$。
- 利用逆向与Quanto-Inverse期权间关系，简化分析焦点为逆向期权本身。

• 经典逆向BS公式引入，与文献[1]中推导相符，特殊之处在于价格表达式非传统BS单调函数。

- 备注：假设4中关于Malliavin导数的阶数和时间间隔依赖对推导隐含波动率偏斜有关键影响。

4. 主定理与分析结果（Section 2-4）

• Theorem 1核心结论：

- 当期权到期时间$T \to 0$，逆向欧式期权ATM隐含波动率$ I(0,k^)$趋近于初始波动率$\sigma0$。
- ATM隐含波动率偏斜$\partialk I(0,k^)$的极限依赖于$H$的大小，$H>1/2$时偏斜消失，$H<1/2$时偏斜随$T^{H-1/2}$发散，但乘以缩放因子$T^{1/2 - H}$后存在极限，表达为积分形式，涉及波动率过程的Malliavin导数期望。

• 逻辑推理：

- 利用Malliavin微积分的预期Ito公式分解期权价格，得出隐含波动率的级数展开及偏斜表达。
- 逆向期权BS价格非单调，需对小期限严格单调区间逆函数性质深入解析（附录B）。
- 波动率与价格的相关性$\rho$直接驱动偏斜该极限值，$\rho=0$时无偏斜。

• 数学表达：见公式(6)、(7)，表明理论上隐含波动率及其偏斜由模型参数和波动率自身行为空间的正则性所决定。

5. 理论推导工具与中间结论（Section 3）

• 关键技术：

- 使用Malliavin微分工具，Clark-Ocone-Haussman公式及预期Ito公式展开逆向期权价格表达式。
- Lemma 1明确定价函数及其导数的有界性和收敛速率，保障积分的绝对收敛，满足应用预期Ito公式条件。

• 价格和偏斜的表达式：

- 期权价格分解为BS定价与校正项，校正项包含波动率的 Malliavin导数加权积分。
- 隐含波动率偏斜（Propositions 1和2）由价格对行权价偏导的导数经链式法则得到，偏斜可用价格函数二阶偏导表达。
- 这些表达式的推导借鉴了作者多篇前期文献[3,5,7]中的技术，但需对应逆向期权独特函数形式做适当修改。

6. 数值模拟与模型应用（Section 5）

• SABR模型：

- 给定SABR参数$\alpha$（波动率波动率）、$\rho$（相关性）和初始波动率$\sigma0$，理论得到ATM隐含波动率偏斜极限为$\frac{1}{2}\rho\alpha$。
- 数值模拟（蒙特卡洛，200万路径，利用antithetic variates降低方差），选用Brent算法反解隐含波动率，结果图（图1,2）显示理论与模拟高度吻合，证明定理正确，同时体现偏斜符号由$\rho$决定。

• 分数Bergomi模型：

- 粗糙波动率模型引入Hurst指数$H$，可离散刻画波动率时间序列的粗糙性。
- 理论结果表明：
- $H>0.5$时 ATM偏斜趋零（平滑波动率，符合经典波动率行为）。
- $H=0.5$时偏斜有限且由$\rho$与$v$（vol-of-vol）决定。
- $H<0.5$时偏斜发散，需乘以$T^{1/2 - H}$缩放后有限，且非线性依赖$H$。
- 数值中，使用Monte Carlo估计短期期权隐含波动率及其偏斜，估计结果显示理论预测的幂律行为大致吻合，数值偏差归因于粗糙噪音导致估计不稳定。

• 实证应用 - Deribit比特币期权：

- 数据来源于2024年5月7日Deribit比特币期权市场，分析多期限，多行权价数据。
- ATM隐含波动率短期期权（1天）约为0.36，符合理论极限。
- 计算市场隐含偏斜，拟合幂律模型$s = c T^{\alpha}$，得到$\alpha=0.3$，对应$H=0.8$，表明市场波动率较平滑，偏斜缓和。
- 该结果排除了SABR模型的适用性（SABR无法捕捉该幂律结构且需$\rho > 0$与普遍观察相悖）。
- 证实粗糙波动率模型为更优选，能较好刻画市场结构。

---

三、图表深度解读

• 图1（第15页）- SABR模型ATM偏斜

- 左图$\rho=-0.3$，右图$\rho=0.3$，曲线为理论偏斜值，点为模拟估计值。
- 图表显示偏斜拟合良好，符号由$\rho$控制，模拟点散布围绕理论线，验证理论正确。

• 图2（第15页）- SABR模型ATM隐含波动率水平

- 模拟估计值点与理论直线高度重合，证明$T\to0$时隐含波动率趋近于$\sigma0$。

• 图3（第17页）- 分数量Bergomi模型ATM偏斜随到期时间变化

- 左图$H=0.4$（粗糙波动率）表现出偏斜发散趋势（趋向$-\infty$）；右图$H=0.7$偏斜趋向0。
- 拟合的幂律指数略有偏差，原因在于粗糙波动率下 Monte Carlo 估计的数值波动。

• 图4（第17页）- ATM偏斜随初始波动率变化（分数量Bergomi模型）

- $H=0.4$时偏斜稳定于负值，$H=0.7$时偏斜为零，均符合理论。

• 图5（第18页）- ATM隐含波动率水平随$\sigma0$变化

- 两个$H$值下，理论与模拟高度一致。

• 图6（第18页）- 比特币期权市场短期期权隐含波动率曲线

- 显示1天到期的隐含波动率随行权价变化，估算初始波动率约0.36。

• 图7（第19页）- 市场ATM偏斜幂律拟合

- 市场偏斜数据点与拟合曲线相近，拟合指数为0.3，支持隐含波动率表面的幂律性质。

---

四、估值分析

该报告核心估值是基于逆向欧式期权的黑—舒尔斯价格框架：

• 利用已知逆向期权BS价格 $BS(t,x,k,\sigma)$，利用Malliavin微积分特殊导数替换标准BS分析。

- 隐含波动率定义为BS价格函数的反函数，因逆向定价非单调，需小到期时间限制确保反函数存在性（详见附录B）。

• 估值方法结合数值蒙特卡洛仿真与隐含波动率反解方法（Brent根搜索法），保证估值精度和效率。

- 估值敏感于：波动率过程动态$\sigmat$、相关系数$\rho$、波动率的波动率（如SABR的$\alpha$与Bergomi的$v$）及粗糙性指数$H$。

• 该方法不直接依赖参数估计，而是通过隐含波动率曲面拟合，连接参数与市场价。

---

五、风险因素评估

• 波动率模型本身的风险：假设1-4为模型适用性和技术要求；若现实市场波动结构偏离，偏斜和隐含波动率估计会有偏误。

- 隐含波动率反函数的非单调性：若期权期限非充分短，隐含波动率可能非唯一，导致难以准确解带来的定价和风险管理复杂性。

• 蒙特卡洛模拟误差和估计波动：特别是在粗糙波动率模型（$H < 0.5$）时，短期模拟易引入高估计偏差。

- 市场流动性与标的资产风险：比特币及加密市场具高度波动和潜在流动性风险，可能超出模型假设范围。

• 相关性假设风险：若实际$\rho$为非恒定或随市场情况变化，则偏斜的定量预测可能失效。

- 报告中对风险缓解未十分详细，更多依赖理论假设和小期限限定来保证模型有效。

---

六、批判性视角与细微差别

• 报告依赖小期限$T\to0$极限，实际市场中期权期限有限，短期限之外的结果推广需谨慎。

- 逆向期权BS价格非单调性导致隐含波动率不唯一性，虽然作者限制了小期限区间，但对中长期隐含波动率的解释尚存不足。

• 数值模拟在粗糙波动率模型下存在估计不稳定性，作者指出这可通过增加样本数或方差削减技术解决，但此处未能体现。

- SABR模型被排除主要基于幂律结构和$\rho$正负号假设，与传统市场经验相矛盾，提醒建模需结合市场情景具体分析。

• 模型假设波动率非交易资产，实际市场中波动率衍生产品日渐丰富，相关模型推广需考虑这一点。

- 报告虽然富有数学深度，但对于实际操盘的风险管理、对冲策略等实务指南较为简略。

---

七、结论性综合

本文系统研究了逆向欧式期权的隐含波动率及其短期期限收敛特性，在随机波动率框架下，利用Malliavin微积分工具，推导得到了：

• 隐含波动率极限收敛性：期权到期时间趋零时，ATM隐含波动率收敛到初始波动率$\sigma0$。

- 偏斜渐近公式：隐含波动率偏斜是否发散严格依赖于波动率粗糙度（Hurst指数H）和资产波动率相关系数$\rho$，阐明了粗糙波动率概念对隐含波动率曲面形态的关键影响。

• 两个典型模型——经典SABR和分数Bergomi粗糙波动率模型的数值模拟验证了理论结论。

- 进一步通过比特币期权市场数据实证，发现市场波动率粗糙度约为$H=0.8$，即较为平滑，表明粗糙波动率模型的实际适用性高于传统SABR模型。

• 图表和公式充分展示了隐含波动率及其偏斜的行为规律，支持交易者理解加密货币逆向期权定价特征及风险管理。

技术上，报告克服了逆向欧式期权价格公式非单调性带来的隐含波动率定义难题，开创了这一领域隐含波动率短期行为的严格理论分析，为加密衍生品定价及波动率建模提供了重要工具和参考。

---

重要图表回顾

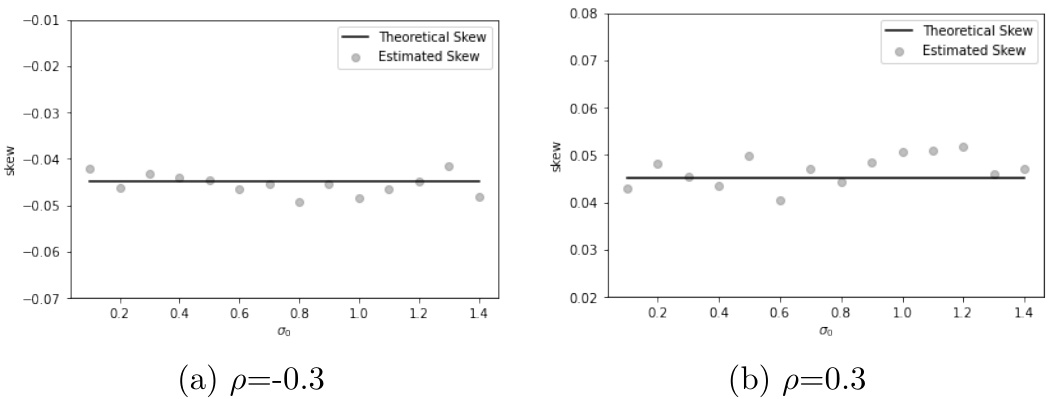
图1显示SABR模型理论偏斜（黑线）和模拟估计（灰点）良好吻合，偏斜符号由$\rho$决定。


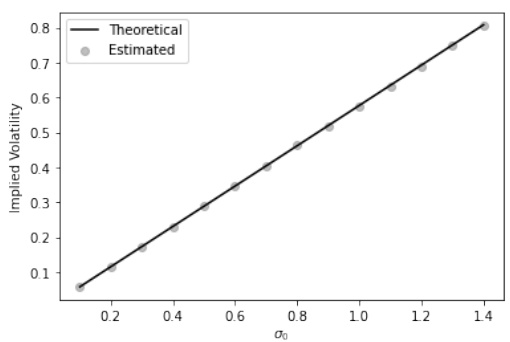
图2展示了理论隐含波动率和模拟估计之间的拟合效果，高度重合。


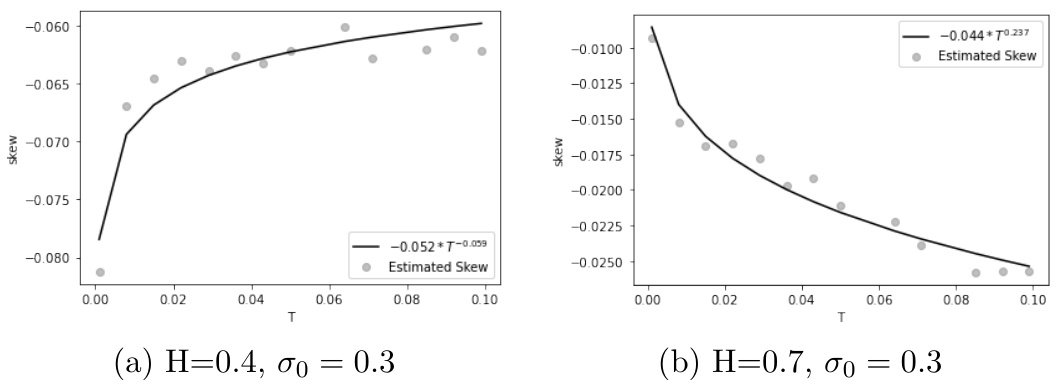
图3展示不同Hurst指数下隐含波动率偏斜表现，粗糙率下偏斜趋发散。


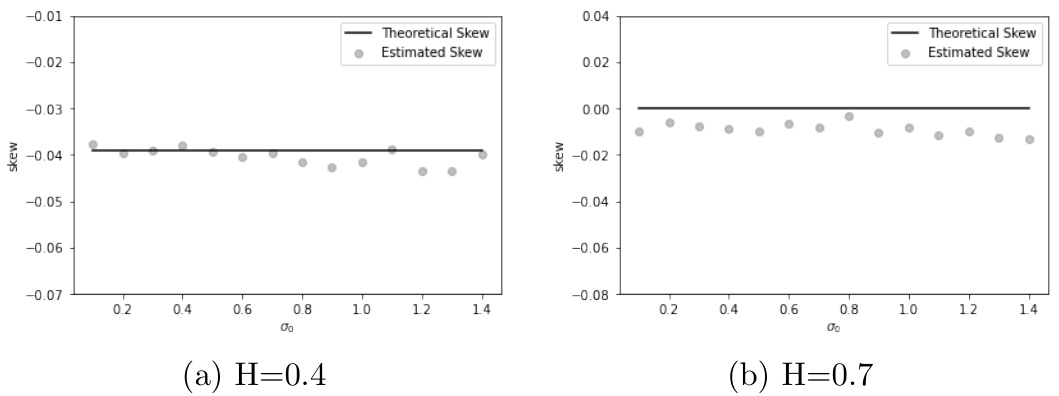
图4展示Hurst指数对偏斜平稳程度的影响，模拟值围绕理论线波动。


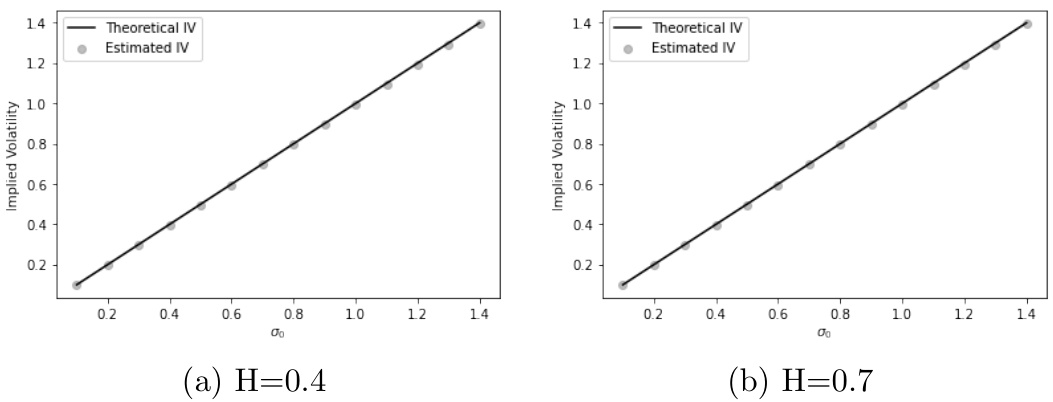
图5显示理论和模拟隐含波动率水平的高度一致性。


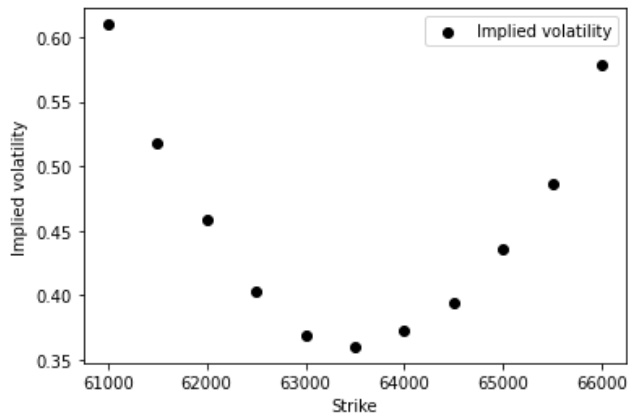
图6为市场实证数据，展示短期（1天）比特币期权隐含波动率随行权价走势。


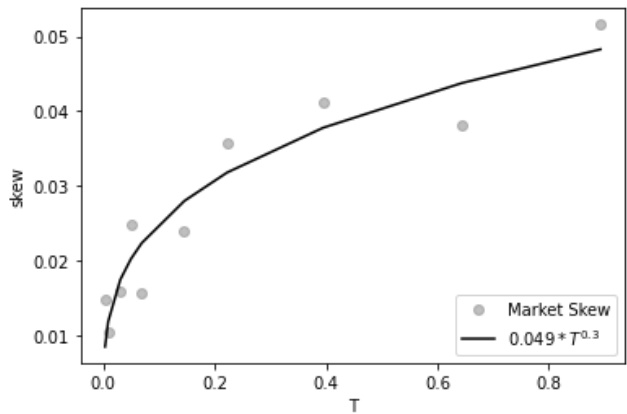
图7表明市场偏斜数据可用幂律很好近似，估计$H\approx0.8$。

---

结语

本研究通过数学严谨的框架与实证验证，开拓了逆向加密期权定价与隐含波动率分析领域，为未来加密资产衍生品的风险管理及市场微结构研究奠定了理论基础和实用指导，具有显著学术与实务价值。未来工作可以进一步拓展隐含波动率曲率等高阶特性，丰富定价和对冲策略，提升模型的实用深度与广度。

---

[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]

报告