• 研究提出了MKABSDE，即带McKean相互作用的前瞻性BSDE，专门用于描述带初始保证金(IM)要求的衍生品定价问题，其中IM基于未来组合价值的条件风险价值（CVaR）[page::0][page::1].

- MKABSDE模型体现了组合价值的非线性和依赖其概率分布的特性，保证了在较宽松的Lipschitz条件下存在唯一解（Theorem 2.1），利用Banach空间上的Picard迭代法证明[page::4][page::5][page::6][page::7][page::8][page::9].

• 在多维Itô市场框架下，将IM作为CVaR函数嵌入BSDE驱动项，实现对带保证金调整的对冲组合价值动态的数学刻画，证明了方程良定性（Corollary 3.1）[page::9][page::10].

- 针对IM追踪窗口Δ较小时，提出利用传统（非前瞻性）非线性和线性BSDE近似模型，并通过Gaussian展开方法给出了误差界估计。主要结论表明，非线性价差误差为O(Δ^2)，而无保证金和有保证金估值差异约为O(√Δ)[page::10][page::11].

• 关键近似BSDE模型：

- (3.5) 非线性BSDE：IM费用基于内生价格的Delta修正项。

- (3.6) 线性BSDE：IM费用基于无IM线性价格的Delta（外生价格）修正。

- (3.7) 标准BSDE：无IM。

• 下述误差估计严格说明了这些近似之间的收敛速率和解的稳定性，有利于实际数值计算的选择[page::11][page::12][page::13].
• 数值算法方面：

- 一维情况下，使用有限差分法高效解算半线性PDE，与BSDE等价，适用于欧式期权价格和Delta计算。

- 多维情况下，采用分层回归蒙特卡洛方法(SRMDP)，可处理高维、非线性BSDE问题，显著缓解维数灾难[page::14][page::15][page::16].

• 数值实验展示了IM调整对期权隐含波动率的显著影响（20-30个基点），并通过不同方法比较保证了算法的准确性，非线性BSDE解定价不满足欧式期权Put-Call对称性，导致隐含波动率曲线异于经典情况[page::17][page::18][page::19].
• 利用嵌套蒙特卡洛算法计算基于线性BSDE的近似解$V^L,Z^L$，通过内外层样本模拟并结合自动微分估计Delta，数值表现与有限差分法接近，适合高维情况[page::19][page::20].
• 高维篮子期权案例（维度2至5）验证了SRMDP算法的稳定性。结果显示包含IM调整后价格与无IM价格接近，说明该方法可支持多资产衍生品风险计算[page::21][page::22].
• 详细理论附录分析了非线性定价下Call与Put隐含波动率不一致的形成机制，关联于受到IM调节的非对称前瞻分布，进一步揭示了波动率微笑的奇异性[page::22][page::23].

报告深度分析报告

报告标题：Numerical Approximations of McKean Anticipative Backward Stochastic Differential Equations arising in Initial Margin Requirements
作者：A. Agarwal, S. De Marco, E. Gobet, J. G. Lopez-Salas, F. Noubiagain, A. Zhou
发布日期：第一版2018年1月29日，最新版本2024年8月5日
研究领域：金融数学，风险管理，衍生品定价，反向随机微分方程（BSDE），条件风险值（CVaR），初始保证金（Initial Margin, IM）
主题背景：本报告主要研究一种新型的、带有McKean型预期依赖（anticipative）的反向随机微分方程（MKABSDE），及其在衍生品定价和初始保证金需求中的应用和数值近似方法。

---

1. 元数据与报告概览

报告聚焦于衍生品市场中的初始保证金(IM)需求对价格和对冲策略的影响，提出了一类新型的MKABSDE，其生成元不仅与当前变量相关，而且与解的分布（law）相关，涉及未来状态的“anticipative”元素。
作者在理论上证明了该类BSDE在广泛条件下的存在性和唯一性，随后针对以CVaR度量初始保证金的实际情况，提出该问题的数学模型，设计了多个数值解法（确定性和蒙特卡罗），并对其进行比较和矩阵求解的实际数值测试。报告的核心信息是：

• 引入MKABSDE刻画考虑基于CVaR的IM所带来的非线性和预期依赖效应；

- 建立MKABSDE的理论基础（存在唯一解），并将其应用于多资产市场场景；

• 提出标准BSDE的线性或非线性近似，结合小时间窗口$\Delta$的尺度，评估不同定价方案之间的误差范围；

- 设计多种数值实现方法（有限差分、SRMDP回归蒙特卡罗、嵌套蒙特卡罗）并通过期权定价实验验证；

• 结果显示IM的引入对期权隐含波动率和价格有显著影响，且数值方法效率较高，适合高维资产定价。

其中，报告没有直接给出明确的买卖评级，而是从理论与数值方法两个层面深度解析与初始保证金紧密关联的非线性BSDE问题，为实际金融机构和监管机构的风险管理决策提供理论工具和数值支持。 [page::0,1]

---

2. 逐节深度解读

2.1. 引言及金融背景（第1章，第1.1节）

核心论点

• 过去金融衍生品的风险中性定价假设已被监管环境影响改变，出现了变动保证金和初始保证金要求以缓解交易对手风险。

- 初始保证金IM定义为覆盖潜在未来风险和对手方违约期间价格风险的保证金，期限通常为10个交易日或一周左右。IM往往按合同价值的CVaR计算，这比VaR更具一致性和数学优越性。

• 报告关注IM对合约定价和对冲策略的内生影响，当IM依赖于合约价值自身时，需用带有分布依赖的预期BSDE建模，即MKABSDE。

- 解决MKABSDE的存在唯一性质后，提出两个IM参考价格的定价原则（内生与外生），并量化它们的近似误差。

• 数值上采用有限差分（1维）、回归蒙特卡罗（多维）、以及嵌套蒙特卡罗实现。

逻辑与假设

• CVaR作为IM的风险度量，强调其符合风险测度的“相干性”；

- IM的时间跨度$\Delta$较短，允许进行小参数渐进分析；

• 价格是解BSDE的随机过程，生成元与CVaR的反馈项相关，从而使BSDE预期且McKean类型（依赖分布）；

- 理论依据建立在BSDE和McKean非线性随机过程理论之上；

• 以模型完全市场假设及适度Lipschitz连续性的假设保证数学可行性。 [page::1]

2.2. MKABSDE示例（第1.2节）

核心论点

• 举例单一资产几何布朗运动，传统微分方程为线性BSDE，其中终端目标为期权支付；

- 引入IM时，BSDE动态增加了基于未来时刻增量CVaR的非线性支付成本，调整了传统发法；

• 该CVaR项显著为条件（预测）风险测度，涉及未来价值$V{t+\Delta}$，是anticipative性质关键体现；

- MKABSDE数学模型具体为方程(1.5)，展示了BSDE的复杂生成元结构。

关键数据或定义

• CVaR条件定义为$$\mathbf{CVaR}{\mathcal{F}t}^\alpha(L) = \inf{x \in \mathbb{R}} \mathbb{E}\left[\frac{(L - x)^+}{1-\alpha} + x \mid \mathcal{F}t \right] $$；

- 期权动态采用几何布朗运动驱动资产和无风险账户；

• IM费率$R$和风控水平$\alpha$为模型参数。

推理和假设

• $V{t+\Delta}$的存在性通过截断为$V{(t+\Delta) \wedge T}$规避边界问题；

- 该BSDE为McKean类型，因为生成元依赖解的分布特征，且是anticipative——用未来信息。 [page::2]

2.3. 不同定价规则比较与文献（第1.3节）

• 作者比较了内生（MKABSDE动态系统内）与外生（市场价值或传统标价）两种计算IM的规则；

- 指出它们的近似误差量级和实际差异，强调理论和实践的平衡。

• 文献回顾涵盖Pardoux-Peng经典BSDE理论、ABSDE（预期BSDE）及其改进与时间延迟BSDE研究；同时比较了Crepey等对相关XVA研究的贡献；

- 本报告区别于以往文献之处，在于着重小时间尺度（$\Delta \approx$1周），并引入MKABSDE的McKean特征和数值近似详细研究。 [page::3,4]

2.4. MKABSDE 的理论构筑（第2章）

• 数学空间及范数定义清晰，便于给出存在唯一解定理；

- 重点给出MKABSDE的形式，解为$(Y,Z)$满足带参数的积分方程；

• Assumption (S)及Assumption (A)明确生成元和依赖非线性算子的Lipschitz条件；

- 主要定理（Thm 2.1）保证了在这些条件下解的存在和唯一；

• 关键的引理（Lemma 2.2）给出不同参数下解之间的稳定性估计，依赖于多参数及常数$\beta,\lambda,\mu$调整；

- 详细证明采用Itô引理、Young不等式、Burkholder-Davis-Gundy不等式和收缩映射原理，体现经典BSDE理论延伸；

• 这些技术对保证MKABSDE问题的数学合理性和求解算法设计基础至关重要。 [page::4-9]

2.5. CVaR初始保证金的MKABSDE应用（第3章）

• 迁移到多维资产Itô市场，对金融市场实际更贴近；

- 给出资产价格及组价动态，一般表述形式包含风险利率、风险溢价及协方差矩阵；

• MKABSDE被具体化为方程形式(3.2)，解为$(V,Z)$，即调整后的标价和对冲过程；

- 以CVaR定义的$\Lambda$算子满足Lipschitz条件，实现Assumption (A)；

• 进一步展开以时间尺度$\Delta$为小参数的近似理论（第3.2节）：

- 基于未来增量用布朗运动近似$Vs - V{s+\Delta}$，将CVaR简化为与$|Zs|$有关的标准BSDE；
- 构建三个BSDE模型：(i) 无IM的经典线性BSDE $(V^{BS},Z^{BS})$；(ii) 以无IM价格的Delta计算IM成本的线性BSDE $(V^{L},Z^{L})$；(iii) 以自身价格Delta计算IM成本的非线性BSDE $(V^{NL},Z^{NL})$；

• 定理3.1给出这三种模型解之间的严格误差界定，显示距离舒适的量级控制：

- $(V^L,V^L)$与经典BS的误差为$O(\sqrt{\Delta})$；
- $(V^{NL},Z^{NL})$与$(V^L,Z^L)$的误差为$O(\Delta)$；
- $(V,Z)$与$(V^{NL},Z^{NL})$误差为$O(\Delta^2)$，在合适正则条件下。

• 这些结果既理论丰富，又极大方便数值计算。 [page::9-13]

2.6. 数值实验（第4章）

• 维度1时，基于半线性抛物型PDE的有限差分法（第四节4.1节）实现非线性BSDE定价，验证准确性；

- 设计了SRMDP（分层回归蒙特卡罗）算法，可扩展至维度较大问题；

• 通过变异减少技巧，用经典Black-Scholes解作为基准，差分解$(V^{DF},Z^{DF})$降低数值方差（4.2节）；

- 嵌套蒙特卡罗方法实现高维度下方程$V^L$的估计，结合沃尔特估计和自动微分技术，通过内层、外层蒙特卡罗减轻计算负担（4.3节）；

• 从维度1到5维均实现了价格和Delta的稳定估计，实证上IM加入显著影响隐含波动率，达到20-30个基点的提升；

- 高频率数据表明SRMDP与有限差分以及理论解高度一致，数值方法成熟可靠；

• 特别是在复杂蝶式期权中体现，IM引发非线性价差，导致隐含波动率曲线双向偏斜，且不满足传统的买卖期权价差对称（put-call parity）关系（详见附录）。

- 图表丰富展示了IM对价格和Delta的影响及各方法误差范围，数值例证充分确证理论。 [page::14-21]

---

3. 关键图表深度解读

图1（页17）

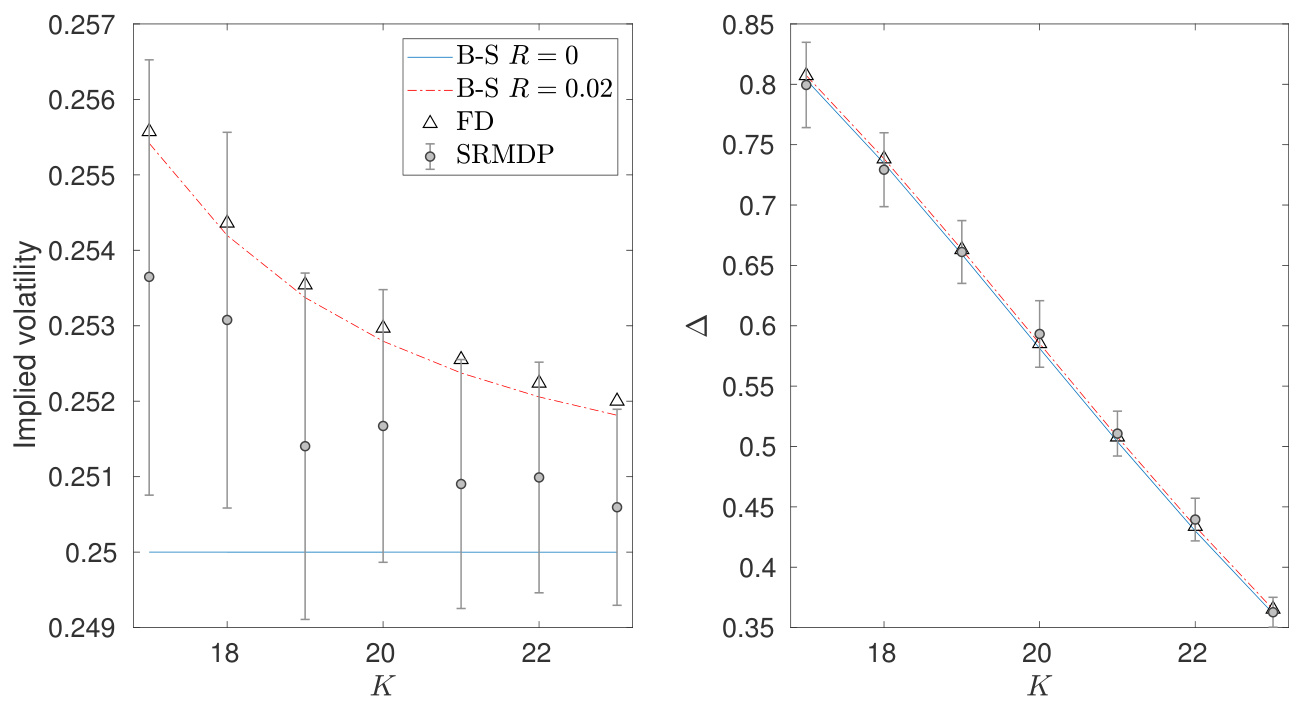
• 显示带IM（$R=0.02$）与不带IM（$R=0$）的不同计算方法下，期权隐含波动率和Delta对执行价$K$的变化。

- 波动率曲线：IM引起整体水平约20-30bps升高，且随着$K$变化趋于平滑递减；

• Delta曲线：三种方法（BS解析、有限差分、SRMDP）高度吻合，体现方法的数值稳定；

- SRMDP置信区间较窄，表明蒙特卡罗方法有效。

• 说明IM成本提高隐含风险预期，导致价格和Delta略有变化。 [page::17]

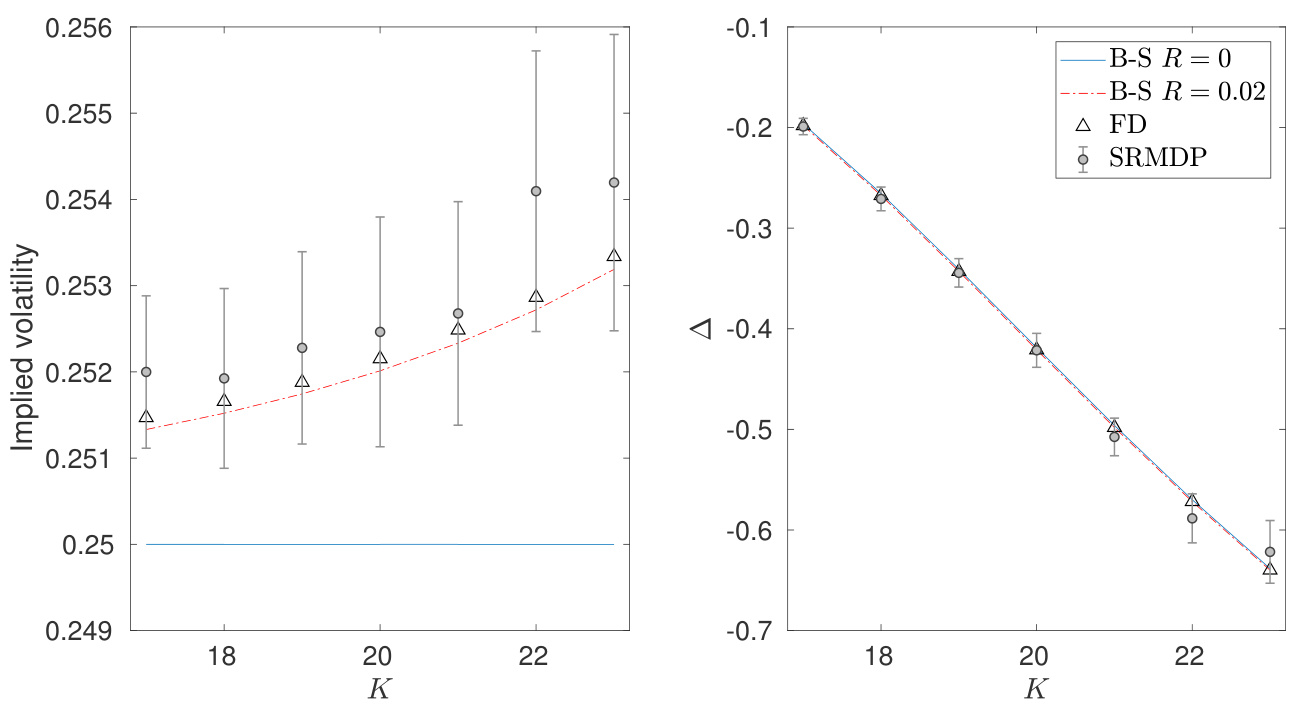
图2（页18）

• 类似图1，但针对看跌期权，显示IM影响期权隐含波动率向上倾斜，Delta呈负斜率；

- IM引入导致看跌的隐含波动率略大于无IM情况，且SRMDP方法置信区间覆盖基准；

• 再次体现定价的非线性复杂性，尤其看跌期权和看涨期权的隐含波动率曲线不对称。 [page::18]

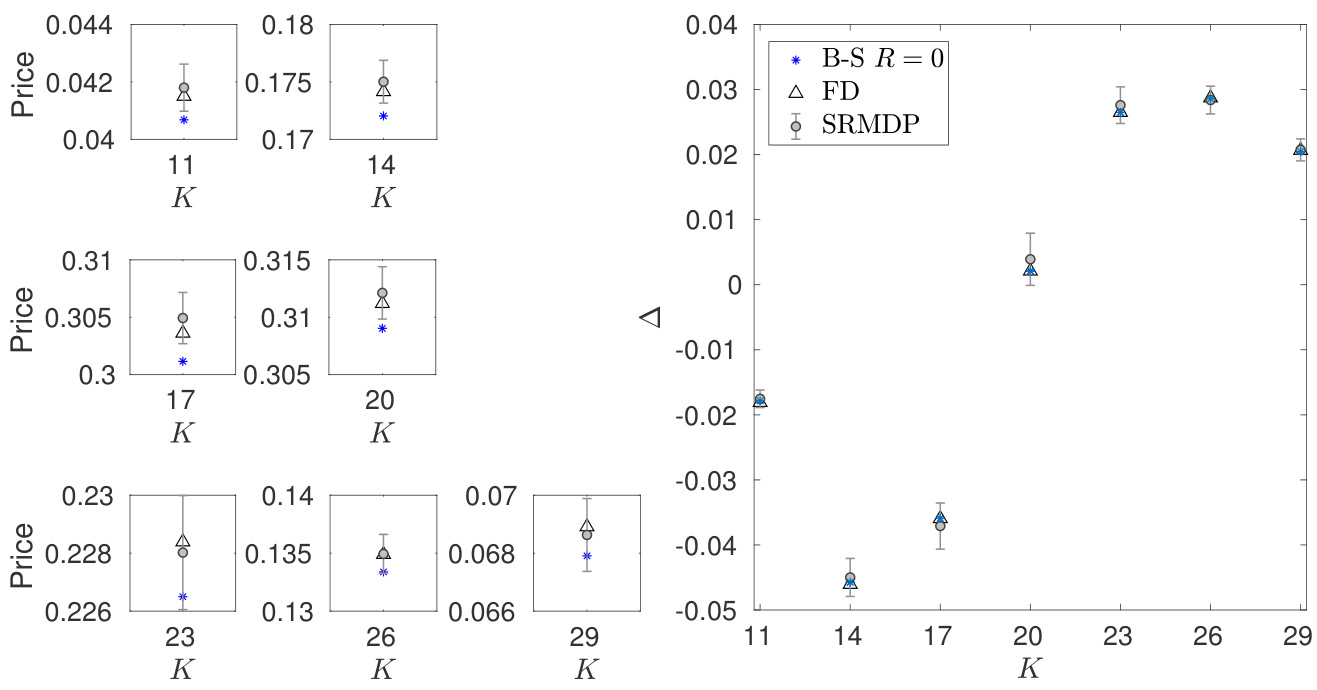
图3（页19）

• 描述蝶式期权不同敲定价对应的价格和Delta，IM介入带来显著价格修正；

- 显示Delta可正可负的复杂形状，经典BS解析法失效，但数值方法（有限差分、SRMDP）仍对比良好；

• IM导致的非线性使定价曲面复杂，反映更精细的市场风险管理效应。 [page::19]

各表格（表1-6，页17-21）

• 表1-3：明细展示不同执行价和期权类型下的价格和Delta估计，带IM和不带IM、不同算法比较，数值一致性良好；

- 表4：差分BSDE$(V^{DF},Z^{DF})$估计结果与解析值（差价）对比，验证方法的偏差降低；

• 表5：嵌套蒙特卡罗估计线性BSDE$(V^{L},Z^{L})$，随机误差区间提供算法效果评估；

- 表6：多资产篮子期权高维SRMDP定价结果，显示算法在高维情况下有效运行，且IM影响价格与Delta细微；

• 这些表格体现了模型对市场假设影响的量化，在不同情形下IM对风险价值和风险管理费用的导出。 [page::17-21]

---

4. 估值分析

• 估值问题自然转化为MKABSDE的解，作为衍生品价格的随机过程；

- 使用 McKean 预期BSDE捕捉IM引起的非线性风险调整；

• 通过小时间置换参数$\Delta$进行渐进展开，将MKABSDE近似为标准非线性BSDE，再线性化为更容易求解的BSDE；

- 线性BSDE带有权重为$\sqrt{\Delta}$的IM成本项，具体由CVaR的标准正态分布数值确定（$C_\alpha$）；

• 收敛与误差控制基于BSDE理论（Pardoux-Peng）和扩展理论（如Zhang 2004）；

- 估值框架包含内生与外生两种IM价格确认方式，通过误差估计比较和数值验证支撑估值方法的选择。 [page::9-13]

---

5. 风险因素评估

• 主要风险因素为IM的计算不确定性，包括对未来市场变化的依赖、量化CVaR时的模型假设；

- 期权价格和对冲策略受到生成元前瞻性（anticipative）变化影响，也即需预测未来风险分布，这在估计时有可能引入偏差；

• 小时间窗口$\Delta$的选择影响近似误差：$\Delta$过大会使线性近似失效，带来较大估值误差；

- 多维度资产相关性和市场参数（如波动率、利率）变化均会影响BSDE求解稳定性；

• 数值算法的蒙特卡罗估计存在随机误差，设置置信区间仍可能不足以捕捉全部计算风险；

- 报告通过理论收敛性和数值对比验证，缓解并控制了这些风险，但实际应用中仍需关注参数敏感性和模型风险，尤其是对远期未来波动性的误判。 [page::3,10-13,14-21]

---

6. 批判性视角与细微差别

• 报告依赖于对CVaR作为IM的度量，尽管Mathematically coherent，但在真实市场中CVaR估计受数据质量和模型假设限制；

- 生成元对分布的依赖提高了建模难度，对分布的估计错误可能导致模型解不稳定；

• MKABSDE框架中终端条件和生成元依赖较强，存在一定的模型递归复杂度，现实中实现需依赖数值方法，数值稳定性待持续关注；

- 报告提及多种数值方法，但未涉及深度神经网络等近年兴起的高维BSDE求解器，未来可拓展；

• IM作为一个多变量、多因子和动态调整特征的指标，报告中假设多为均匀时间窗口且缩小至小量$\Delta$，实际交易中会受到操作风险和流动性风险影响，模型未完全涵盖；

- put-call parity不成立的非对称性及隐含波动率差异为非线性定价的一个必然结果，需风险管理层进一步关注此类模型对于交易策略的实操影响。 [page::22-24]

---

7. 结论性综合

本报告提出并系统研究了基于McKean类型预期BSDE（MKABSDE）的衍生品定价方法，将金融市场中对初始保证金（IM）的复杂风险度量（CVaR）纳入BSDE生成元，实现了从理论建构到数值验证的闭环。

关键发现与贡献包括：

• MKABSDE新数学结构，预期BSDE结合分布依赖，真正捕获了IM的内生风险调整特征；

- 理论上证明了MKABSDE的解的存在和唯一，具备良好稳健性，为金融定价提供坚实理论基础；

• 通过渐进分析，近似为标准BSDE，显著提升计算可行性及效率，适合实际应用；

- 多种数值方法如有限差分、SRMDP回归蒙特卡罗和嵌套蒙特卡罗，针对低维和高维资产的定价问题均证明有效，数值结果与理论极为吻合；

• IM的加入明显提升期权隐含波动率，导致价格变动幅度显著，且破坏了传统的put-call parity，引发波动率微笑的非对称现象；

- 高维篮子期权问题展示了该方法对实际复杂场景的适用性；

• 所有方法的误差级别明确，为未来进一步模型优化和风险管理提供参考标准。

整体来看，作者在理论建模、数值算法和金融应用之间实现了深度融合，为监管指令下的衍生品风险度量与定价提供了创新且实用的数学工具。报告不仅填补了MKABSDE理论空白，也为银行及监管机构设定可靠的初始保证金定价和风险管理框架奠基。





---

溯源注释标记：[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]

报告