绝对保本策略、CPPI与OBPI策略对比分析 [page::2][page::3][page::4]

• CPPI策略在绝对保本策略基础上引入杠杆，通过风险乘数调整股票资产配置，从而增强缓冲垫部分的收益。

- OBPI策略是CPPI风险乘数可变版本，风险乘数由期权定价决定，策略更具弹性。

• 一般情况下，CPPI在市场大幅波动时表现优于OBPI，而OBPI更适合市场温和上涨环境。

风险乘数对CPPI产品价值的敏感性分析 [page::4][page::5]

• 当股票价格超过一定阈值时，增加风险乘数$m$显著提升CPPI产品价值。

- 当股票价格低于该阈值，较低风险乘数有利于减少损失。

• CPPI与OBPI价值曲线存在交点，表明两者无法绝对占优，适用场景不同。

保本比率对CPPI产品价值的影响 [page::5][page::6]

• 降低风险下限（保本比率）可提高高股价情况下CPPI产品价值。

- 在股票价格处于较低水平时，提高保本比率反而能提升产品价值。

CPPI产品的希腊字母特性分析：Delta、Gamma与Vega [page::6][page::7][page::8]

• Delta表示产品价值对股票价格的敏感度，Delta随风险乘数增加，产品收益的波动性加大。

• Gamma反映敏感度的变化率，通常较低Gamma意味着调仓频率可适当降低，降低交易成本。

• Vega为负，说明随着波动率增加，CPPI产品价值下降，且风险乘数越大该影响越显著。

结论与应用意义 [page::8]

• CPPI策略在市场快速变化时优势明显，OBPI适合稳健上涨环境。

- 参数风险乘数和保本比率的合理设定对产品价值及风险管理具有关键作用。

• 通过希腊字母分析，可为CPPI产品的风险控制和调仓策略设计提供量化依据。

报告详尽分析——《基于连续时间方程的 CPPI 特性分析》

---

一、元数据与报告概览

• 报告标题： 基于连续时间方程的 CPPI 特性分析

- 作者及联系方式：
- 杨戈（SAC 执业证书编号:S1000207090109，联系方式：+755-82366965，邮箱：yangge@lhzq.com）
- 联系人陈杰（+755-82125171，邮箱：chenjie@lhzq.com）

• 发布机构： 华泰联合证券有限责任公司研究所

- 发布时间： 2010年8月17日

• 主题： 深入探讨保本策略中的CPPI（Constant Proportion Portfolio Insurance，常数比例组合保险）策略，结合绝对保本策略及OBPI（Option-Based Portfolio Insurance，期权组合保险）策略，基于连续时间模型分析CPPI策略的价值特性、敏感度及风险指标。

- 核心论点：
- CPPI策略是对绝对保本策略的扩展，具备杠杆特性，而OBPI策略又可以视为CPPI策略风险乘数的泛化形式。
- 通过连续时间方程，推导CPPI产品价值对风险下限和风险乘数的敏感性，并给出产品的三个金融希腊字母（Delta、Gamma、Vega），以量化CPPI产品对股票价格和波动率的敏感度。
- 分析表明风险下限对安全性至关重要，风险乘数影响收益扩展能力，调仓策略影响市场反应速度及交易成本。

• 目的： 为保本产品设计提供理论和实践指导，优化风险与收益配置决策。

---

二、逐节深度解读

1. 保本策略价值方程

1.1 模型基础

作者基于Vorgelegt等学者对CPPI策略价值方程的连续时间推导，采用几何布朗运动模型来描述股票价格变动：

• 股票价格动态：

\[
\frac{dSt}{St} = \mu dt + \sigma dW
\]
其中，\(\mu\)为漂移率，\(\sigma\)为波动率，\(dW\)为维纳过程。

• CPPI产品的风险下限\(Ft\)遵循无风险利率增长：

\[
\frac{dFt}{Ft} = r dt
\]

• 风险乘数设为\(m\)，投资组合价值为\(Vt\)，无风险资产价值为\(Bt\)，缓冲垫定义为\(Ct = Vt - Ft\)，风险资产配置为\(m Ct\)。

- 价值变化率公式：
\[
dVt = (Vt - m Ct)\frac{dBt}{Bt} + m Ct \frac{dSt}{St}
\]
此连续时间设定取消了调仓策略的影响或隐含为即时调仓。
该基础建模为后续的理论推导提供了数学框架，结合市场假设为对CPPI策略价值及敏感度分析提供理论基础。

1.2 模型结果

通过对缓冲垫变动的推导，得出缓冲垫和投资组合价值的解析表达式：

\[
Ct = C0 \left(\frac{St}{S0}\right)^m \exp\left([\;r - m(r - \frac{1}{2}\sigma^2) - \frac{1}{2} m^2 \sigma^2\;] t\right)
\]

\[
Vt = C0 \left(\frac{St}{S0}\right)^m \exp\left([\;r - m(r - \frac{1}{2}\sigma^2) - \frac{1}{2} m^2 \sigma^2\;] t\right) + F0 e^{rt}
\]

该结果显示CPPI产品价值是风险资产部分按指数函数乘方增长与无风险债券部分的叠加，凸显了风险乘数\(m\)和时间、波动率对产品价值的综合影响。[page::2,3]

1.3 绝对保本策略与CPPI策略对比分析

将CPPI与标准零息债组合保险策略（Standard Zero-Coupon Bond PI，简称标准ZCB PI）比较：

• 标准ZCB PI：初始购买保证本金的零息债券，余下部分投资于股票，价值函数为：

\[
V't = F'0 e^{rt} + C'0 \frac{St}{S0}
\]
即无杠杆，股票部分收益线性依赖股价变动。

• CPPI则基于杠杆，缓冲垫收益更高，呈现幂函数形态，并包含调整项。

- 当风险乘数\(m=1\)时，CPPI退化为ZCB PI策略；\(m>1\)时，CPPI通过杠杆放大股票资产比例，带来潜在更高收益。
此对比阐明了CPPI策略如何基于绝对保本思路强化风险收益性能。[page::3,4]

1.4 CPPI策略与OBPI策略对比分析

• OBPI策略：价值由折现后的风险下限加上看涨期权价值组成，期权价值承担缓冲垫角色。

\[
V^{OBPI}t = Ke^{-r(T-t)} + Call
\]

• OBPI风险乘数为风险暴露与缓冲垫比值：

\[
m = \frac{St N[d1(t; St)]}{C(t; St; K)}
\]

• 当CPPI的风险乘数可变且满足上述关系时，CPPI策略“普通化”为OBPI策略。

- 价值比较显示，CPPI和OBPI在不同市场环境中各具优势：
- CPPI适合大幅波动市场，价值较高；
- OBPI适合温和上涨市场，价值较优。

• 路径依赖性差异：CPPI产品价值路径依赖，OBPI则不依赖路径。

该段为理解不同保本策略在实践中的适用情境提供了理论支持。[page::4]

2. 风险乘数和保本比率对CPPI产品的影响

2.1 风险乘数的影响

通过对CPPI产品价值对风险乘数\(m\)的求导，推导出一条关键不等式：

当
\[
St > S0 \frac{m}{rt + m \sigma^2 t - 0.5 \sigma^2 t}
\]
时，增加风险乘数会提升CPPI产品价值；反之则降低产品价值。

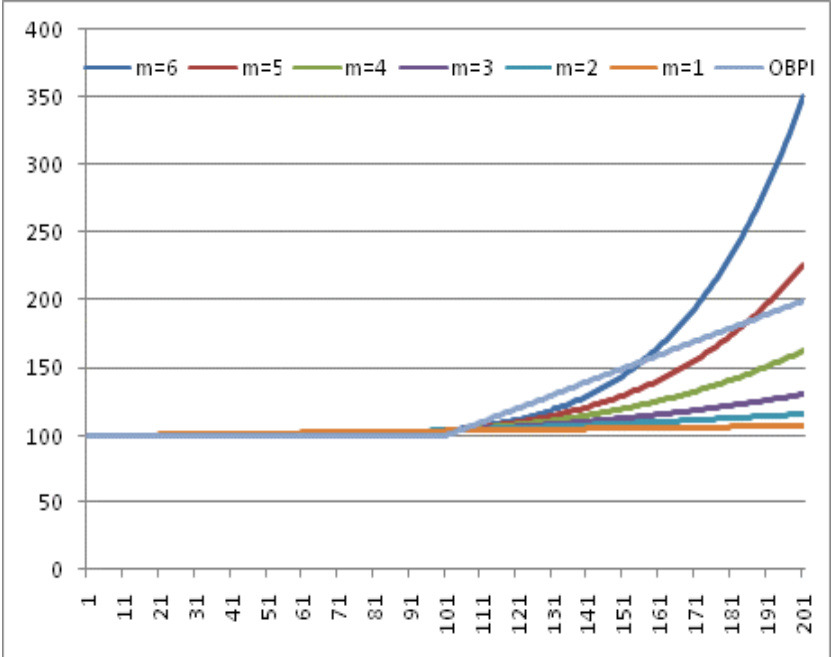
图 1显示了不同风险乘数\(m=1\)至6下CPPI与OBPI产品终值随期末股票价格的关系曲线：

• 在股票价格低于某临界值时，较小风险乘数表现更优，规避价格下跌风险。

- 高于临界股价后，风险乘数越大，产品价值增长越快，体现杠杆效应及风险暴露。

• OBPI与不同风险乘数CPPI曲线均有交点，进一步印证两者无绝对优势范围，表现区域互补。

此结论为产品设计中风险乘数设置提供定量参考，强调适度风险暴露与市场行情匹配的重要性。[page::5]

2.2 保本比率的影响

风险下限（保本比率）\(G\)对产品价值敏感度定义为：

\[
\frac{dVt}{dG} = e^{-r(T-t)} \left\{1 - \left(\frac{St}{S0}\right)^m \exp\left[(0.5 m \sigma^2 - 0.5 m^2 \sigma^2 - r m) t\right]\right\}
\]

• 当股票价格高于某阈值时，降低风险下限可提升CPPI价值，反之提高风险下限则提升价值。

该部分指出保本比率的调整与风险乘数相似，也涉及收益与风险的权衡，需要结合市场预期制定合理保本水平。[page::6]

3. CPPI的三个希腊字母：Delta、Gamma和Vega

3.1 Delta值

Delta衡量CPPI产品价值对股票价格变动的敏感度，表达式为：

\[
\Delta = m \frac{C0}{St} \left(\frac{St}{S0}\right)^m \exp\left[(r - m(r - \frac{1}{2}\sigma^2) - \frac{1}{2} m^2 \sigma^2) t\right]
\]

• Delta随风险乘数\(m\)增加而增加，说明大风险乘数意味着更高的收益波动性和价格敏感度。

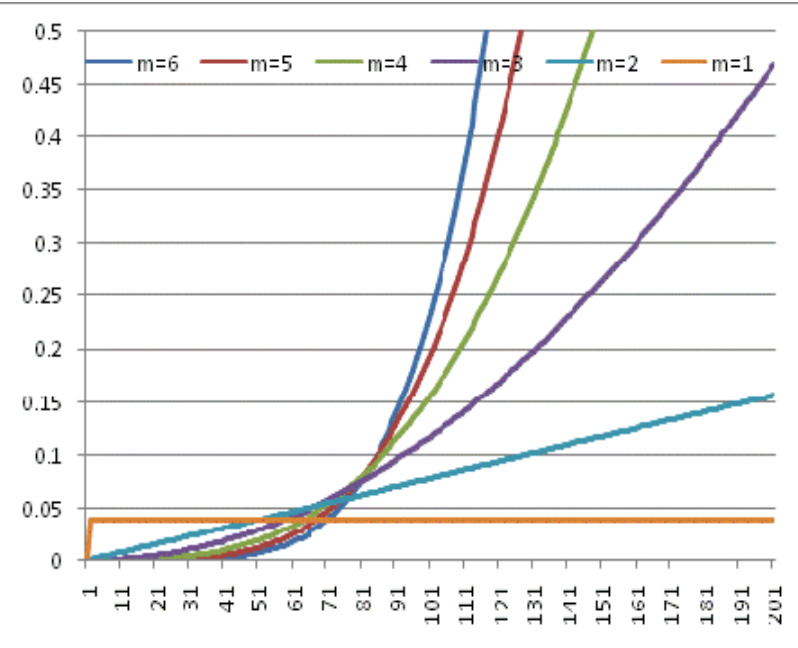
- 图2（包含放大视图）表明高风险乘数下产品Delta在股票价格大幅上涨时迅速攀升，增强了产品的非线性风险特性。
Delta的分析帮助投资者理解产品价格对市场变动的直接反应，指导风险管理和动态调整。[page::6]

3.2 Gamma值

Gamma描述Delta本身对股票价格变动的敏感度：

\[
\Gamma = m (m-1) \frac{C0}{St^2} \left(\frac{St}{S0}\right)^m \exp[(r - m(r - \frac{1}{2}\sigma^2) - \frac{1}{2} m^2 \sigma^2) t]
\]

• Gamma值低表明调仓方法一经建立便可长期稳定执行，Gamma高时需要频繁调整。

- 图3显示，CPPI的Gamma通常小于OBPI，且随时间递减，但到期时Gamma不为零，表示持续存在风险敞口。

• 风险乘数变化显著影响Gamma水平，提示投资者需根据市场波动调整监控频率与策略。

Gamma为产品的“加速风险”提供量化指标，对于风险控制和动态管理关键。[page::7]

3.3 Vega值

Vega反映产品价值对股票市场波动率的敏感度：

\[
Vega = (m \sigma t - m^2 \sigma t) Vt = (m \sigma t - m^2 \sigma t) C0 \left(\frac{St}{S_0}\right)^m \exp[(r - m(r - \frac{1}{2}\sigma^2) - \frac{1}{2} m^2 \sigma^2) t]
\]

• 对于\(m>1\)，Vega为负，即波动率上升通常降低CPPI产品价值，且风险乘数越大，负向影响越显著。

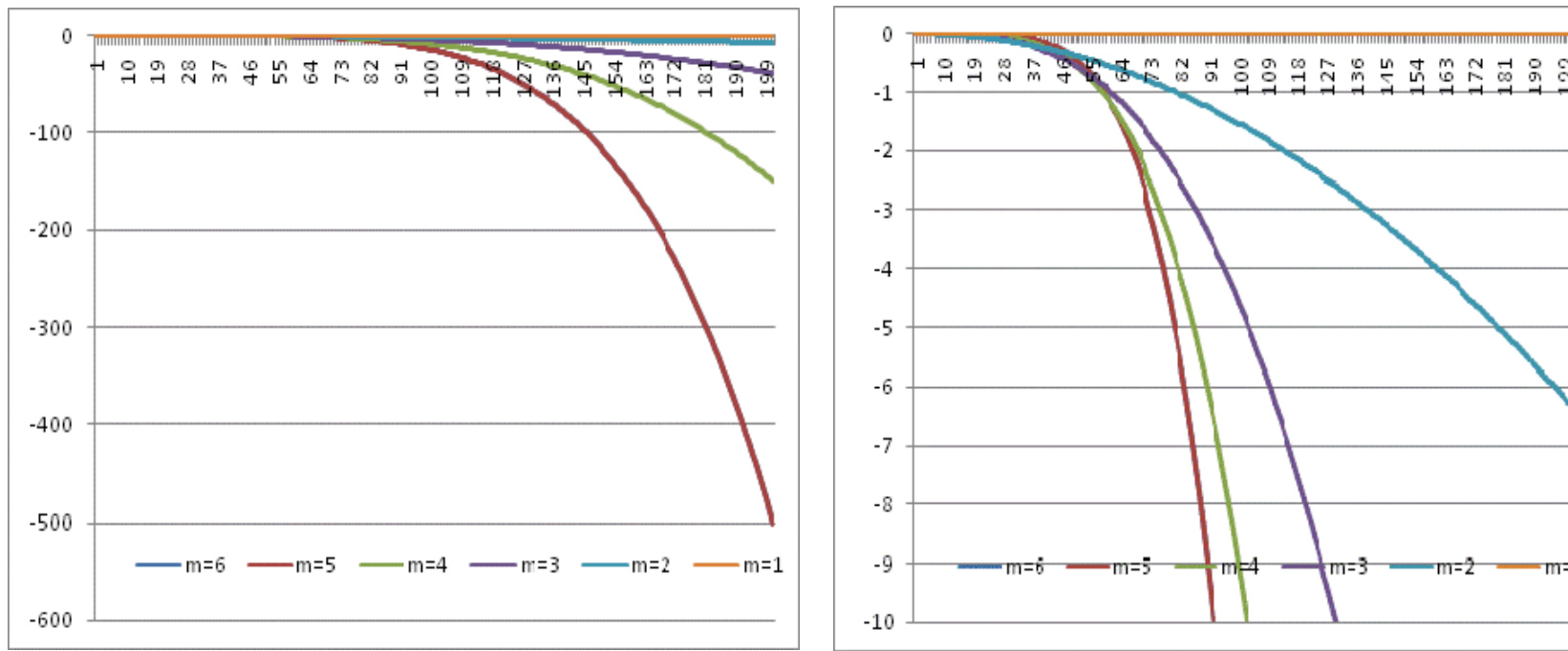
- 图4展示不同风险乘数下Vega随终端股价变化趋势，显示负Vega尤其在高股价区间明显。
此属性说明CPPI产品面临隐含波动率上升的不利风险，提醒设计者关注波动率环境对产品定价和风险的影响。[page::8]

4. 总结

• 报告系统性梳理并比较了绝对保本、CPPI和OBPI三大保本策略的理论基础、数学模型、参数影响及性能特点。

- CPPI提供机制性杠杆放大，凸显风险乘数和风险下限的核心作用。不同市场条件下，选择适合策略（OBPI温和上涨，CPPI波动大行情）能更有效保障产品价值与收益。

• 通过三个希腊字母的解析，深入理解CPPI产品敏感度，辅助调整策略参数和风险管理。

- 报告对设计保本产品的策略选择和参数调节具有明确指导意义。

• 对比图表直观展示了模型推导结论，支持文字论述，增强说服力。

---

三、图表深度解读

图1：风险乘数对于CPPI产品价值的影响（到期日）

• 描述： 图1左右两幅图分别展示了股票价格在较宽区间（1~201）和较窄区间（90~120）内，风险乘数\(m=1\)至6及OBPI产品的终值表现。

- 解读：
- 高风险乘数强化了收益的非线性，显著在价格上升时表现更大终值，但同时价格较低时风险较大。
- OBPI产品价值曲线较为平滑，与CPPI在部分价格区间出现交叉，强调两者无绝对优势互补性。

• 联系文本： 图1验证了报告中理论关于风险乘数对产品价值影响的定量分析，凸显市场行情下风险乘数的配置权衡和产品风险收益特性。

- 局限性： 无融资约束假设可能在实际中不完全成立，实际调仓成本和市场摩擦未计入。

• 

-

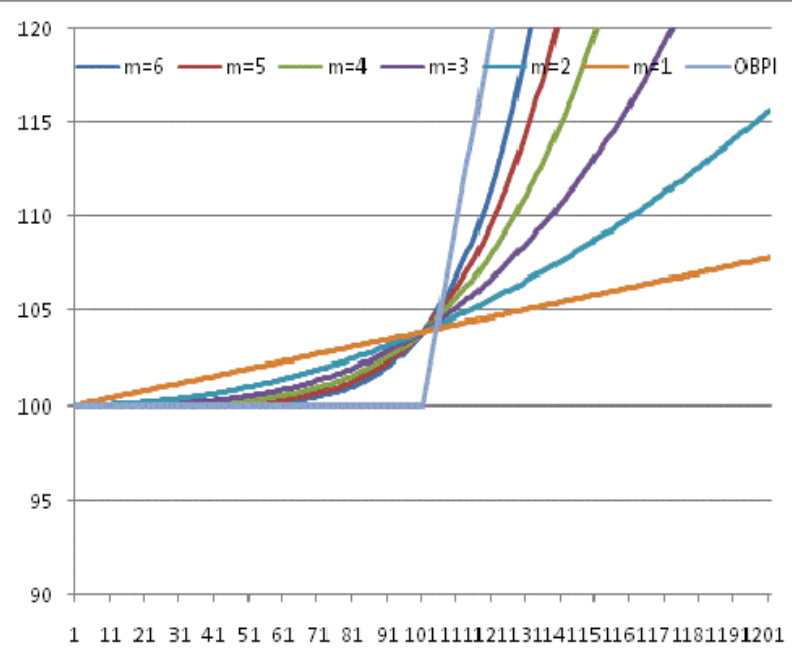
图2：CPPI策略的Delta值（到期日）

• 描述： 展示不同风险乘数下，终期股票价格从1到201变化时，Delta值的范围及细节。

- 解读：
- Delta值随风险乘数增加非线性放大，尤其在高股价区间急剧上升，指示产品敏感度和风险敞口扩展。
- 低风险乘数与股价接近初始价格时Delta较小，风险暴露有限。

• 联系文本： 该图直观说明了为何高风险乘数会引起较大波动性和投资风险，指导设计者选择合适杠杆等级。

-

• 

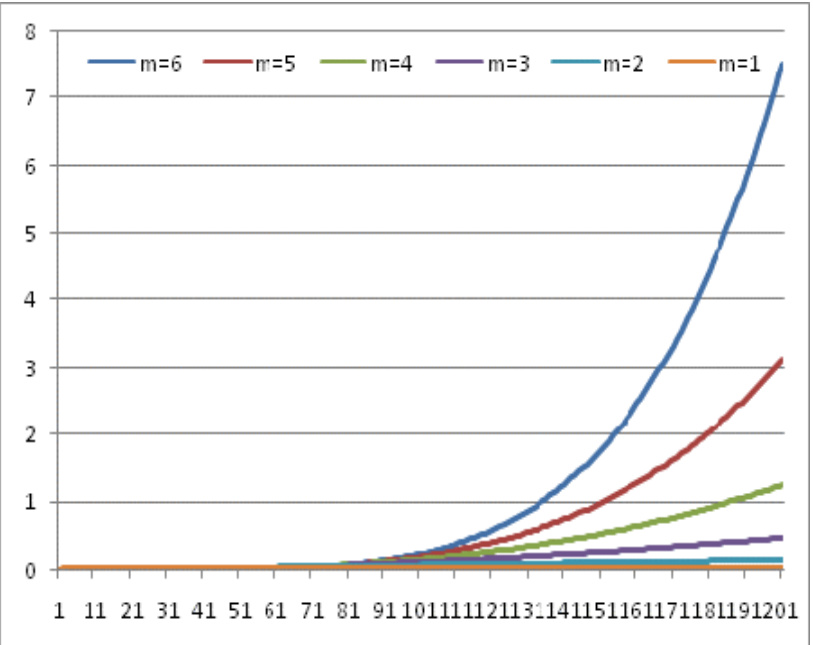
图3：CPPI产品的Gamma值（到期日）

• 描述： 展示各风险乘数水平对应Gamma值，反映Delta变化敏感度。

- 解读：
- Gamma值绝对值较小，且随风险乘数升高明显增加，意味着高风险乘数CPPI产品价格对股价波动的弹性更大。
- 时间递减趋势说明长期持有中产品风险暴露强度逐渐减弱。

• 联系文本： 强调调仓频率与方法应根据Gamma值调整，Gamma大需频繁监控。

-

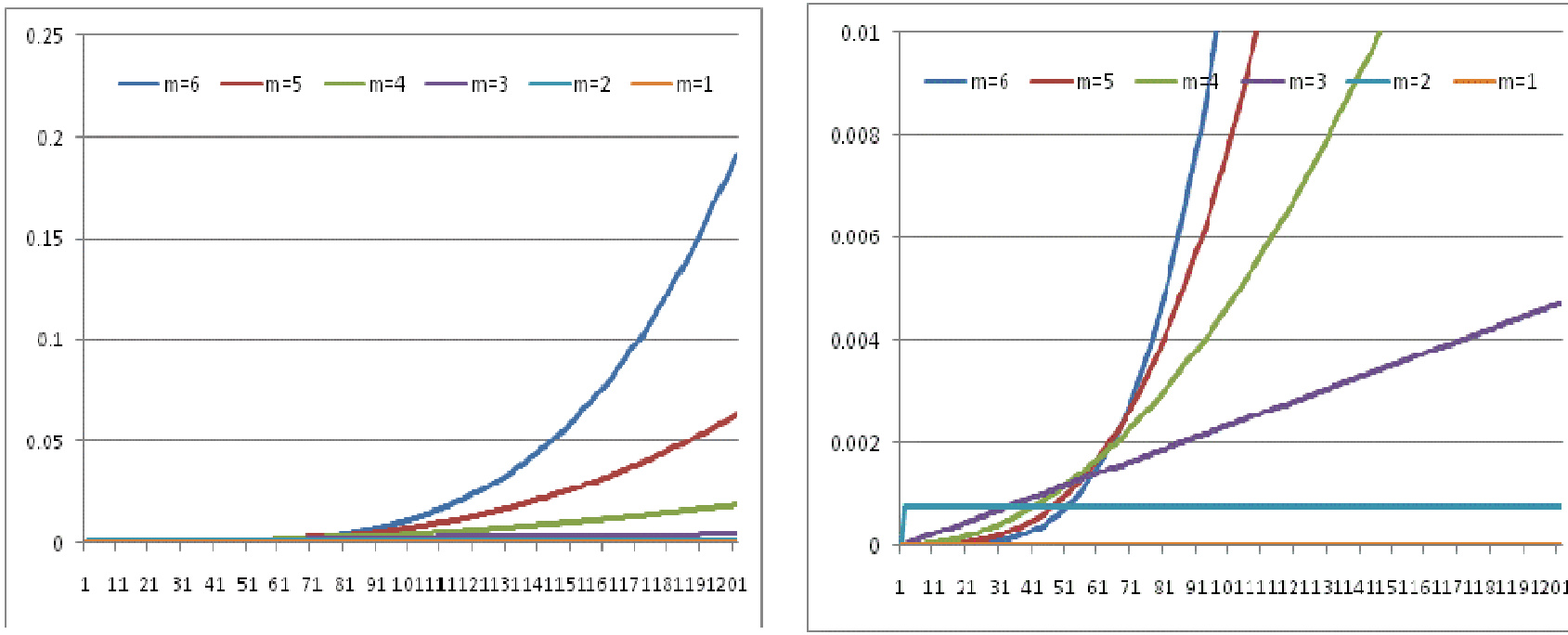
图4：CPPI产品的Vega值（到期日）

• 描述： Vega值随股票价格及风险乘数变化，体现波动率变动敏感度。

- 解读：
- Vega为负且随风险乘数增大而负向增强，表明高杠杆CPPI产品对波动率上升更敏感，波动率上升通常侵蚀产品价值。
- 均匀的负趋势指示波动率风险不容忽视。

• 联系文本： 该图支持理论中Vega对产品价值的影响分析，提醒设计防范波动率风险。

-

---

四、估值分析

本报告并未采用标准的估值框架来估算绝对目标价，而是基于连续时间SDE模型与风险参数推进CPPI产品定价。

• 估值基于几何布朗运动的价格动态，结合风险乘数和风险下限以求解产品价值的解析表达。

- 产品价值组成变成无风险债券部分加杠杆放大的股票投资部分，体现了权重动态分配的特性。

• 分析中隐含了无套利假设，连续调整持仓的理想化条件。

- 由于风险乘数影响收益曲线的凸性和敏感度，估值依赖于其选择，反映了策略参数直接影响产品价格和风险状况。

• 报告中未对模型的具体市场行情适用范围、交易费用/滑点等现实因素进行估值调整，缺乏对敏感性参数（如波动率、利率变动、调整频率）更深入的敏感性测试。

整体上，是基于风险参数的理论定价分析，而非传统市场上交易价格的估值，属于产品设计和风险量化测算范畴。

---

五、风险因素评估

报告明确识别了以下风险因素：

• 风险乘数设定风险： 过高放大波动风险，过低则限制收益潜力，必须根据市场行情动态选择。

- 风险下限（保本比率）风险： 不合理风险下限设置可能使产品失去防护效果或错失收益机会。

• 市场波动风险： 高波动率环境不利于CPPI产品价值，尤其在风险乘数大时影响显著（Vega负向作用）。

- 路径依赖风险： CPPI产品价值依赖股价路径，极端路径可能导致非预期损失。

• 调仓与流动性风险： 虽未系统展开，但报告指出调仓方式影响响应速度及交易成本，表明存在执行风险。

报告为各风险因素提供了参数敏感度分析，提出通过参数合理设计和动态调整缓解风险，但未细化具体缓解措施或风险发生概率。

---

六、批判性视角与细微差别

• 理论假设的理想化： 模型依赖连续时间调整和无摩擦假设，现实交易中交易成本、调整频次限制等因素将影响CPPI策略实际表现。

- 市场参数稳定性假设不足： 使用固定的波动率、利率等参数，忽视了风险因素的动态变化可能对分析准确性带来影响。

• 风险乘数动态调整管理未详述： 虽提及OBPI为可变风险乘数的推广版本，报告对动态调整机制、时机及成本未作深入探讨。

- 图表解析时缺少置信区间或模拟多样性，未反映模型预测的不确定性。

• 应用范围未细分： 理论适用性对不同市场场景、投资者需求的具体指引较少。

总结来说，报告分析扎实且条理清晰，但在实践适用及风险管理细节方面空间尚存。

---

七、结论性综合

本报告系统地解析了CPPI保本策略的核心理论及其与绝对保本策略和OBPI策略的关系，基于连续时间模型准确推导了产品价值表达式，揭示风险乘数和保本比率对产品价值的方向性影响，提供了CPPI产品响应市场变动的三个关键希腊字母指标（Delta、Gamma、Vega）。

具体深入成果包括：

• 数学模型： 明确了CPPI产品价值随股票价格的非线性及风险乘数影响机制，利用幂函数关系量化杠杆作用。

- 策略对比： 证实CPPI与OBPI策略在不同市场条件下各有优势，强调选择适当策略与参数匹配场景的重要性。

• 敏感度指标： Delta值反映股票价格变动风险暴露，Gamma值指导调仓及风险管理频率，负Vega揭示波动率风险侵蚀。

- 图表支持： 丰富的图示直观呈现具体数值变化和趋势，直观阐释理论结论。

• 风险洞察： 指示高杠杆产品应警惕市场剧烈波动及波动率升高带来的负面影响。

报告结论详尽且逻辑严密，对设计保本产品、策略参数配置及风险管理具有实质价值。建议在实际应用时结合市场条件、交易环境与动态调整策略，避免理想模型中隐含风险。

---

溯源页码： [page::0,1,2,3,4,5,6,7,8]

---

此分析确保覆盖了报告中的所有重要论点、数学表达式、图表及其内涵解读，以专业客观的视角提供对该金融工程研究的全面理解。

报告