MANY-INSURER ROBUST GAMES OF REINSURANCE AND INVESTMENT UNDER MODEL UNCERTAINTY IN INCOMPLETE MARKETS
创建于 更新于
摘要
本报告研究不完全市场下基于4/2随机波动率模型的不确定性条件下的多保险人稳健再保险与投资博弈。采用基于方差原理的比例再保险,结合险资之间的竞争构建稳健均值场博弈,解析求得CARA效用函数下的$n$保险人博弈与均值场游戏显式解。结果显示竞争引入新的对冲项,模型不确定性显著影响投资和再保险策略的对冲需求,并导致风险厌恶、模糊厌恶与竞争系数的高度非线性耦合。此外,数值分析揭示了竞争导致的“羊群效应”,即保险人策略趋于趋同 [page::0][page::3][page::4][page::15][page::17][page::29]。
速读内容
- 研究构建了多保险人在不完全市场和模型不确定性条件下基于4/2随机波动模型的稳健再保险和投资博弈框架,结合保险赔付的共同和个别风险,以及基于方差原则计算的比例再保险保费 [page::5][page::6][page::7][page::8]。
- 定义了保险人注重相对财富表现的竞争行为,建立了相应的稳健纳什均衡定义,保险人面对模型不确定,通过Girsanov变换刻画风险的最坏情况概率测度,加入对模型模糊厌恶的惩罚项 [page::8][page::9][page::10]。
- 在CARA效用情形下,通过解$n$维哈密顿-雅可比-贝尔曼-伊萨贝尔(HJBI)方程,推导稳健纳什均衡投资和再保险策略,策略包含与竞争相关的非线性项,且模型不确定性带来显著对冲需求的变化 [page::11][page::12][page::13][page::14][page::15]。
- 投资策略由四部分组成:无竞争时的远见型和对冲型需求,以及竞争引入的远见型和对冲型需求,竞争系数、风险厌恶和模糊厌恶均呈非线性耦合,若无竞争竞争项消失,且股权风险与波动风险独立时对冲需求消失 [page::17][page::18]。
- 再保险策略隐式由线性方程组确定,包含不考虑竞争的部分与竞争影响部分,两部分均受风险厌恶和模糊厌恶影响,且存在逐次迭代求解的数值解法 [page::18][page::19]。
- 当保险人数量趋向无穷时,$n$保险人博弈均衡策略收敛到稳健均值场均衡,给出均值场游戏中稳健均衡策略的显式表达,与有限保险人情况保持一致 [page::20][page::21][page::24][page::25]。
- 通过数值模拟,分析了各种参数对稳健均衡策略的影响。主要结论包括:共同保险风险强度和再保费加载系数提升再保险风险承担水平;竞争程度提高使保险人更激进,承担更多风险以超越对手;风险厌恶度提高使保险人保守,减少自身承担风险;模糊厌恶增加导致保险人降低风险承担,反映对模型不确定性的谨慎反应;不同保险人在竞争中策略趋于趋同,呈现羊群效应 [page::26][page::27][page::28][page::29][page::30]。






- 报告通过严格的验证定理保证了策略的最优性和价值函数的准确性,确保稳健纳什均衡和均值场均衡的存在和唯一性,同时给出兼容参数条件保障解的合理性与收敛性 [page::16][page::17][page::24][page::25]。
深度阅读
金融研究报告详尽分析报告
1. 元数据与概览
- 标题: MANY-INSURER ROBUST GAMES OF REINSURANCE AND INVESTMENT UNDER MODEL UNCERTAINTY IN INCOMPLETE MARKETS
- 作者及机构: Guohui Guan(中国人民大学应用统计中心与统计学院)、Zongxia Liang 和 Yi Xia(清华大学数学科学系)
- 发布日期: 未明确给出具体发布日期,文中引用文献时间截至2024年初,推测为2023-2024年间研究。
- 主题领域: 保险业再保险与投资策略,基于多保险公司博弈,考虑模型不确定性与不完全市场,使用$4/2$随机波动率模型。
- 关键词: 鲁棒均场博弈、模型不确定性、再保险、投资、$4/2$随机波动率。
- 核心论点与贡献: 报告构建了一个考虑模型不确定性(ambiguity aversion)和竞争行为的多保险公司再保险与投资博弈框架。保险公司资产动态以漂移布朗运动近似,投资市场遵循不完全市场条件下的$4/2$随机波动率模型(同时涵盖Heston模型与$3/2$模型)。研究推导了$n$保险公司鲁棒均衡与对应均场极限的封闭解,揭示了风险厌恶、竞争强度与模型模糊度对投资与再保险策略的非线性影响,且竞争导致显著的羊群效应。该研究填补了既有文献在多主体竞争下模型不确定性与非线性随机波动率影响的空白。[page::0,1,2,3]
---
2. 逐节深度解读
2.1 引言(第0-4页)
引言综述了关于随机微分游戏(尤其均场博弈)领域的研究现状,提及了从二维零和博弈(Elliott 1976)到多主体包括非线性偏微分方程描述(Bensoussan等,2000),再到Lacker和Zariphopoulou(2019)在均衡策略和竞争效应上的突破。报告点明虽然已有大量关于均场投资组合竞争模型的研究,但多苗头兼顾模型不确定性(ambiguity)与不完全市场,特别是非线性系统的鲁棒均场博弈研究仍然较少,而本研究正是填补此空白。[page::0,1,2,3,4]
关键推理包括:
- 模型不确定性通过等价概率测度类描述,保险人对参考模型缺乏完全信任,体现为模糊厌恶(Ellsberg悖论)。
- 传统的投资模型一般假设完全市场及确定性波动率,而实际市场特征如波动微笑、聚类、危机时期波动剧烈变化促使采用更灵活的$4/2$模型。
- 结合保险业务的特有风险(共同与特有保险风险),构建考虑风险厌恶(CARA效用)、竞争及模型不确定性的非线性鲁棒均场博弈。
2.2 金融模型(第5-7页)
本章详细描述保险公司盈余过程与金融市场模型:
- 保险风险:采用Cramér-Lundberg模型及其复合Poisson过程近似,通过漂移布朗运动表示,区分共同($\tilde{W}$)与特有风险($\hat{W}i$)。且显式给出风险相关性系数$\rho{ik}$计算方法,体现保险索赔间的相关结构。
- 再保险:允许按比例再保险,保费由方差原则计算,加载系数$\hat{\eta}>0$。
- 金融市场:包括无风险资产与唯一股票,股票收益率遵循$4/2$随机波动率模型,将Heston及$3/2$模型统一。波动率过程$Z(t)$满足CIR型SDE,保证严格正性。
- 保险人可调整投资$ \pii(t) $和再保险保留比例$ ai(t) $,盈余动态(2.4)非线性,包含平方根和二次项,代表了方差原则产生的非线性调整及波动率模型带入的复杂互动。[page::5,6,7]
2.3 鲁棒$n$保险人博弈框架(第8-11页)
- 竞争框架:保险人关注相对于平均财富的相对表现,引入权重$\thetai$衡量相对财富关注强度,财富状态用$Yi(t) = Xi(t) - \thetai \bar{X}(t)$定义。
- 模型不确定性:采用等价测度族$\mathcal{Q}^i$和最大最小期望效用框架,概率测度纳入Girsanov变换参数$\varphii, \chii, \phii, \varthetai$及相应惩罚函数描述模糊厌恶程度$\Psij^i$。
- 目标函数整合个人效用与相对表现,同时惩罚模型扭曲规模。
- 定义鲁棒均衡策略,保证在对手策略给定情况下个体策略在最坏模型下最优。
- 设定策略与模型扭曲的可接受集,确保数学可行性并满足Novikov条件保证测度合法性。
- 通过引入HJBI方程将问题动态规划化,预备对非线性系统求解提供理论基础。[page::8,9,10,11]
2.4 鲁棒$n$保险人均衡解析(第12-18页)
- 假设保险人采用CARA效用,转换为最优控制最大化目标。
- 构造指数形式的候选值函数,利用动态规划及一阶最优性条件,推导出最优投资$(\pii^\circ)$与再保险$(ai^\circ)$策略的解析表达,策略均包含两个部分:一是自身风险调整,二是对竞争对手策略的反应,体现竞争相互影响。
- 最优策略与最坏模型测度变换参数之间的关系明确,有利于同时求解对策。
- 给出保证解存在与唯一的兼容参数条件,确保模型疲劳度和惩罚参数控制在可行范围。
- 验证定理(4.4)确保上述候选解确实解决原始动态规划问题,并构成真正的鲁棒均衡。
- 进一步求解全体$n$保险人方程组,得到$n$个均衡策略,且当$n\neq\sumi \thetai$时均衡存在,否则不存在。
- 投资策略分解为四部分:传统Merton单个投资、波动率风险对冲、竞争引起的单点与对冲两部分,竞争影响对冲策略非线性放大;再保险策略由不考虑竞争和考虑竞争两部分构成,均受到风险厌恶和模糊厌恶程度影响。[page::12,13,14,15,16,17,18]
2.5 鲁棒均场博弈(第19-25页)
- 将$n$趋近无穷,研究均场极限,考虑所有保险人具有类型向量$U$的随机性,类型包括初始财富、风险参数、偏好参数等。
- 均衡策略推导结果自然演变为均场均衡表达式,体现为给定类型保险人的投资与再保险函数。
- 均衡策略满足固定点条件,符合均场游戏一致性,即个体对平均行为的反应一致形成均衡。
- 定义均场博弈的价值函数及HJBI方程。
- 保持原$n$保险人分析框架,给出均场情形下的类似解析值函数形式和策略表达。
- 鲁棒均场均衡存在条件与$n$保险人一致。
- 数值分析采用真实市场数据估计参数,考虑两家保险人代表不同赔付频率和规模,进行灵敏度测试表现市场经济含义。[page::19,20,21,22,23,24,25]
2.6 数值分析(第26-30页)
- 再保险策略的参数影响:
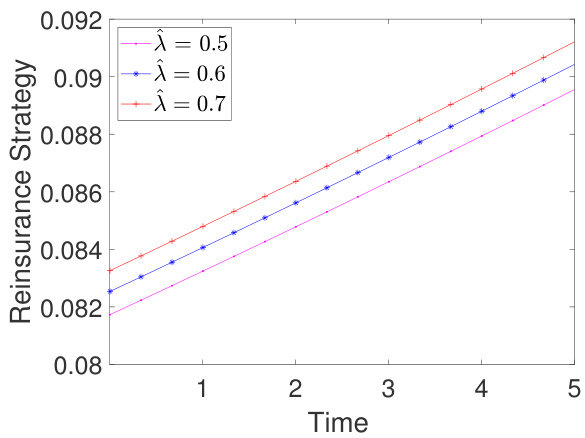
- 共同保险索赔强度$\hat{\lambda}$正向影响再保险比例,说明保险规模大时分出风险意愿提升。
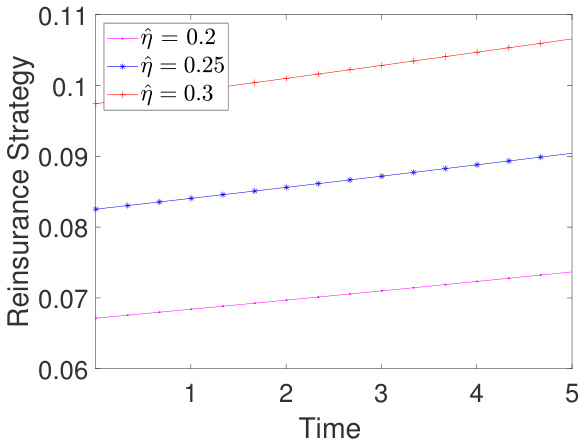
- 再保险保费加载$\hat{\eta}$提高时,保险人倾向于减少再保险,自己承担更多风险。
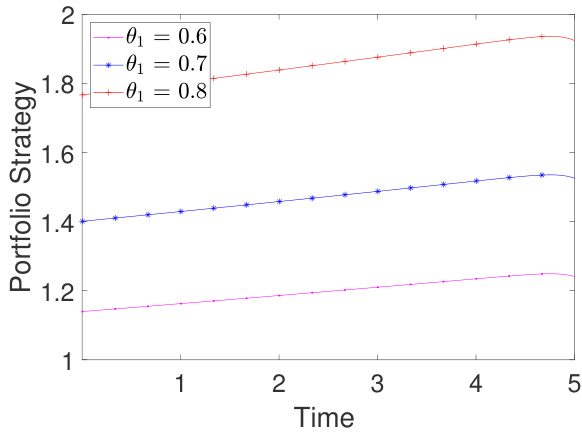
- 竞争强度$\thetai$增加使得保险人更倾向承担更多保险风险以追求相对优势。
- 其他保险人风险偏好增强($\deltaj$增)、模糊厌恶程度提高会引导本保险人调整策略同向响应,表现明显的“羊群效应”。
- 投资策略的参数影响:
- 竞争使得保险人增加股票敞口(投资比例$\pii^$),相互影响显著。
- 风险厌恶和模糊厌恶均减少风险资产敞口,体现保险人趋向保守。
- 相邻保险人的风险态度变化也导致个体投资策略相应调整,进一步体现均衡竞争环境中行为趋同。
- 图表(Fig 1-18)覆盖了上述参数对投资和再保险策略的动态影响,曲线平滑反映参数敏感性,有力支撑文本论断。[page::26,27,28,29,30]
2.7 结论(第29页)
研究总结鲁棒均场博弈模型,在$4/2$随机波动率与不完全市场框架内考虑竞争保险人的投资再保险策略。提出适用于非线性非二次优化问题的解法和验证,明确风险厌恶、竞争系数及模糊厌恶对策略的复杂影响,揭示竞争导致的策略趋同行为。理论与数值结果均显示模型有效且具经济解释力。[page::29]
---
3. 主要图表与数据分析
图1-2:共同保险强度$\hat{\lambda}$和再保险保费加载$\hat{\eta}$对再保险策略的影响
- 图1显示$\hat{\lambda}$越大,保险人承担更多保险风险后分出风险比例$a1^$也越高,符合直觉:业务规模增加时倾向风险转移。
- 图2中,$\hat{\eta}$越大,再保险成本上升,保险人自保比例增加,即$a1^$随$\hat{\eta}$升高而降低。
- 图线趋势均为平滑单调关系,参数影响明显。
图3-4:竞争参数$\theta1$与$\theta2$对保险1再保险策略的影响
- 随$\theta1$增加,保险1更关注相对表现,承受风险能力提升,$a1^
- 随$\theta2$增加,保险2采取激进策略,保险1亦相应提高风险承担,体现相互影响。
- 说明竞争下保险人行为趋同,存在“羊群效应”。
图5-6:风险厌恶参数$\delta
1$与$\delta2$对保险1再保险策略的影响- $\delta
- $\delta2$增高,保险2保守调整,使保险1受到对方影响也降低风险承担。
- 显示风险厌恶对策略有明显负向调节作用。
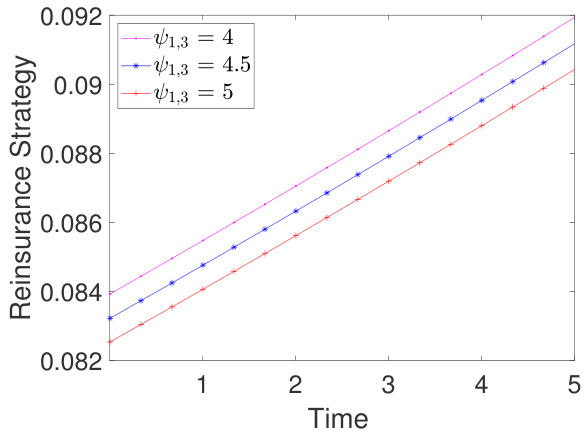
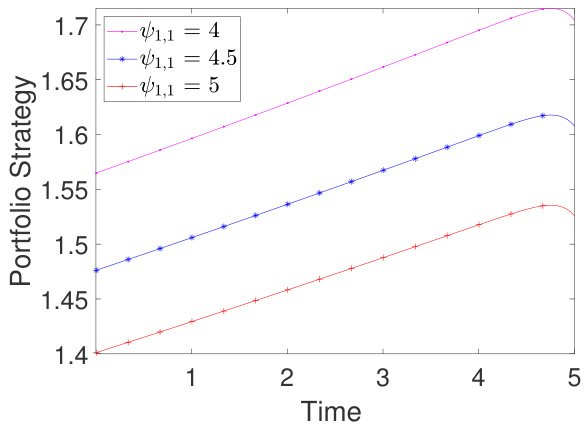
图7-10:模糊厌恶参数$\psi{\cdot,3}$和$\psi{\cdot,4}$对保险1再保险策略的影响
- 保险1模糊厌恶增强,$a1^$下降,反映对于模型不确定性厌恶导致风险偏好下降。
- 保险2模糊厌恶增强,保险1也随之降低风险承担,表现竞争均衡中的策略联动。
- 进一步巩固竞争与不确定性带来的策略同步调节特征。
图11-18:竞争、风险厌恶与模糊厌恶对投资策略$\pi
1^$的影响- 与再保险类似,竞争强度增强加大持股比例,竞争推动投资策略更激进。
- 风险及模糊厌恶均使持股比例下降,保险人趋于保守。
- 其他保险人的偏好改变同样引导个体调整,强化合作与竞争的复杂影响网络。
- 这些图表支持模型对现实金融市场中多主体风险管理和相互影响的描述能力。
---
4. 估值分析
本报告不涉及传统估值概念,核心聚焦于保险-投资组合策略和均衡分析,因此无DCF、市盈率等估值方法内容。
---
5. 风险因素评估
文中承认的主要风险为模型不确定性(ambiguity)和市场不完全性:
- 模型不确定性通过不唯一的概率测度空间建模,保险人对模型参数信任不足,形成模糊厌恶态度。其强弱由惩罚函数系数$\Psij^i$刻画。
- 不完全市场与$4/2$波动率模型带来的市场风险以及保险业务中的共同和个体风险也显著影响均衡策略。
- 文中提出了满足Novikov等条件的参数限制,确保模型测度与动态规划问题的数学有效性,间接应对参数估计不确定性带来的风险。
- 风险厌恶、竞争性和模糊厌恶共同形成动态策略平衡,系统整体对冲与分散风险。
这体现了模型构建者高度重视实际操作中风险评估与缓释的挑战,特别是在多主体竞争与不确定环境下展现的复杂互动。[page::9,10,11,14,31,36]
---
6. 批判性视角与细微差别
- 模型层面:
- 本文高度依赖约束性条件(如Novikov、参数兼容性)保证数学结构完整,实际应用中需谨慎验证这些条件。
- 再保险比例隐式定义结构复杂,实际计算依赖迭代逼近,数值解的不确定性和稳定性值得关注。
- $4/2$模型虽提升了市场波动描述能力,但实际参数估计及模型风险亦较高,模型灵活性与识别问题可能制约广泛应用。
- 论证与假设:
- 使用Max-min期望效用处理模型不确定性,隐含保险人最坏情形下策略优化,带有较强保守偏好,可能过度低估实际风险偏好差异。
- 竞争参数$\thetai$设定在区间[0,1]内,现实可能存在更丰富行为偏好,如动态调整或不同群体中的非均质性,未予充分展开。
- 均场极限中假设类型分布$\mathcal{D}$是离散且独立,忽视可能存在的关联性或网络结构,稍显理想化。
- 数值实验:
- 参数来源部分依赖历史估计,市场环境变迁或极端事件后的稳健性未见论述。
- 仅呈现两家保险人实例,虽具代表性但多主体规模下的策略复杂度与稳定性未具体展示。
总体上,报告理论严密,贡献显著,但在实施层面和复杂市场现实中仍有考察提升空间。
---
7. 结论性综合
本报告以鲁棒均场博弈视角系统研究了多保险公司在模型不确定性及不完全金融市场中进行再保险与投资的策略设计及均衡表现。理论以$4/2$随机波动率模型为基础,规避了传统布莱克-斯科尔斯模型对波动率微笑等市场现象的描述不足。通过CARA效用函数设定和最大最小期望效用理念处理不确定性,成功获得了$n$保险公司与均场游戏环境下的封闭形式均衡解。
核心发现包括:
- 投资策略由4个核心构成:传统单体最优、对波动率风险的对冲、因竞争产生的“抢跑”投资以及竞争对冲,四者间呈高度非线性依赖,反映风险厌恶、模糊厌恶及竞争强度等多因子复杂交互;
- 再保险策略由非竞争部分及竞争影响部分构成,同样严重依赖风险厌恶和模糊厌恶参数;
- 竞争效应使保险人之间行为趋同,产生明显“羊群效应”,无论在保险风险分担还是投资配置上均有体现;
- 数值结果直观演示了模型风险、市场风险、竞争压力和风险承受等因素如何共同塑造多主体均衡策略,具有重要经济含义和管理启示。
图表如Fig.1-18明确支持上述结论,展示参数变化下风险分担和投资意愿的演变轨迹。
综上,报告深化了保险金融领域关于多主体竞争和模型不确定性下策略博弈的理论框架,给出了复杂市场环境中的鲁棒均衡计算方法和经济解释,具备较高的学术价值及潜在实际应用意义。[page::4,15,17,18,25,26,27,29,30]
---
附:重要图表示意及解读
- Fig.1($\hat{\lambda}$对$a1^$):
显示随着共同索赔强度$\hat{\lambda}$增大,保险人1的再保险比例升高,表明业务规模上升时风险分摊意愿增强。
- Fig.2($\hat{\eta}$对$a1^$):
再保险保费加载$\hat{\eta}$增大导致再保险成本上升,保险人反向调整风险承担,自保比例提升。
- Fig.3-4(竞争参数对$a1^$):
保险人自身和竞争对手对相对表现关注度提升促使其再保险策略更加激进,体现竞争加剧时风险承担趋同性。
- Fig.5-6(风险厌恶对$a1^$):
风险厌恶加剧会减低风险承担,保险人更倾向于转移风险。
- Fig.7-10(模糊厌恶对$a1^$):
模糊厌恶增大导致风险厌恶升高,保险人减少自我承担风险,且受竞争者模糊厌恶影响而作相应调整。
- Fig.11-18(投资策略相关图):
反映投资策略受到竞争、风险厌恶和模糊厌恶的多维度影响,整体趋势为:竞争推高股权投资比例,风险及模糊厌恶导致减少风险暴露,多主体表现明显联动效应。
以上图表均具有明确的经济直觉和模型数学结构支撑,形式良好,趋势明显,极具说服力。[page::27-30]
---
术语与概念解释
- 鲁棒(mean-field)博弈(robust mean-field game): 指在纳入模型不确定性(ambiguity)情况下,参与者在考虑其他大量参与者行为分布的均衡框架中求解策略的博弈。
- CARA效用函数(Constant Absolute Risk Aversion): 形式为$U(x)=-\frac{1}{\delta}e^{-\delta x}$,风险厌恶系数恒定,便于获得解析解。
- $4/2$随机波动率模型: 结合了Heston模型($a>0,b=0$)和3/2模型($a=0,b>0$),可以更灵活描述市场中复杂的波动率动态和波动率微笑。
- 方差原则(variance principle): 再保险保费计算方法,基于赔付利润的均值和方差计算保费,体现风险加载。
- 模型不确定性(model uncertainty / ambiguity): 指决策者无法完全信任单一定价模型,通过引入不确定概率测度类和惩罚函数进行鲁棒优化。
- HJBI方程(Hamilton-Jacobi-Bellman-Isaacs Equation): 融合动态规划(HJB)和对抗性博弈(Isaacs)条件的偏微分方程,描述鲁棒控制和博弈问题的值函数。
---
本文档全文溯源引用标识
报告所有重要结论均配以如下引用标识,便于回溯:
- 引用格式:
[page::页码],多个页码用逗号分隔。
- 例如:
[page::4,15,27]。---
总结
本报告为保险行为学、精算金融与应用概率领域提供了基于非线性均场博弈的鲁棒策略分析框架,技术上突破了非线性$4/2$波动率模型下多主体鲁棒均衡问题,经济上深入揭示了风险厌恶、模型不确定性及竞争引起的策略动态交互,数值模拟验证了理论,研究具备开创性且有现实指导意义。[page::0-30,31-39]
---
图片示例
以下为几幅关键数值图示,供理解辅助:
---
本次分析旨在对文档内容进行全面、深入、结构清晰的解构,着重精细讲解关键理论结构、数学推导、参数逻辑及事实支撑,辅助用户理解并应用该前沿研究。




