• Chakraborti庭院买卖模型核心机制：多个相同代理人通过随机两两交易，转移较贫代理人财富的固定比例，且交换期望财富不变（鞅性质）。最终财富几乎必然凝聚至唯一代理人，形成极端不平等[page::0][page::1]。

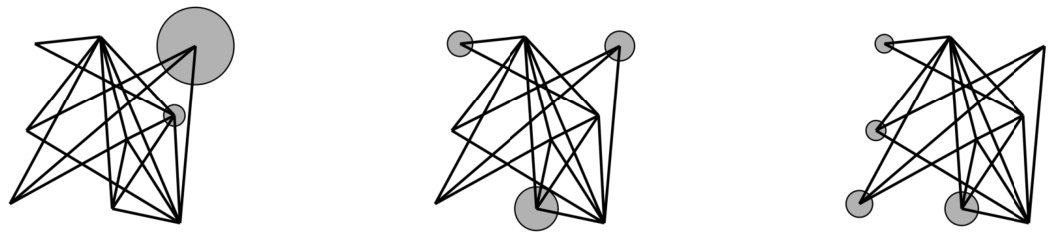
- 本文引入不完全图结构限制交易对，导致财富局部凝聚，即少数代理人富裕且互不交易，贫穷代理人为其邻居，改变了传统模型的全局凝聚特征。示意图展示多个模拟结果中财富局部集中分布：

[page::2]

• 研究将交易中财富转移比例与交易偏好视为随机变量，允许历史依赖，定义交易中加权概率$p\ell$与风险参数$B\ell$，不再保持鞅结构，扩展模型适用场景[page::2][page::3]。

- 关键创新点为分析财富向量的Euclidean范数$\|X\ell\|^2$变化，推导条件期望差分表达式：

$$
E(\|X\ell\|^2 - \|X{\ell-1}\|^2 \mid \cdots) = (4p\ell-2) B\ell X{\ell-1}^{\mu\ell} (X{\ell-1}^{v\ell} - X{\ell-1}^{\mu\ell}) + 2(B\ell X{\ell-1}^{\mu\ell})^2
$$

在公平（$p\ell=1/2$）和财富优势（$p\ell>1/2$）下该式始终非负，支持财富凝聚趋势[page::3][page::4]。

• 对于部分贫困优势（$p\ell<1/2$）情况，提出约束条件(不等式7)来保证该期望也保持非负，扩展了传统鞅方法无法处理的场景[page::4]。

- 通过Borel-Cantelli引理证明下注资产$X{\ell-1}^{\mu_\ell}$几乎必然收敛到0，进而在图的边结构限制下证明财富分布向集合$\mathcal{C}$（财富非零代理不相邻）收敛，形成局部财富凝聚现象（定理2）[page::4][page::5]。

• 讨论部分指出本模型清晰且具一般性，可容纳交易对选择和风险参数的历史依赖，且提供严格的数学证明。因此，极端财富不平等可由纯随机交易机制产生，无需假设代理人能力差异[page::5][page::6]。

- 研究未包含传统量化因子构建或量化投资策略，但从概率和数学建模视角深化了财富交换模型的理论基础。

深度分析报告：《Local wealth condensation for yard-sale models with wealth-dependent biases》

---

1. 元数据与报告概览

• 标题：《Local wealth condensation for yard-sale models with wealth-dependent biases》

- 作者：Christoph Börgers（塔夫茨大学数学系）、Claude Greengard（Two Sigma Investments及纽约大学Courant数学科学研究所）

• 发布机构：学术论文，未见明确期刊信息，包含参考文献显示最新研究动态

- 主题：基于Chakraborti的“yard-sale model”（摊位交易模型）的财富分配动态，特别是带有财富依赖偏差的模型中财富聚集（wealth condensation）现象的数学证明及扩展

• 核心论点：

- 该文提出了新的、相较于传统使用Doob鞅收敛定理更为初等的数学证明方法，证明在储蓄模型中财富必然向少数代理集中（即财富凝聚）。
- 新方法不仅适用传统公平硬币投掷的模型（无偏财富转移），还适用于带有财富依赖偏差（包括财富优势和贫困优势）的模型。
- 论证隐含着不论交易网络结构如何（完整图或不完整图），贫富差距的聚集现象都会出现，且具有一定的局部财富凝聚性质。

• 目标：通过数学严谨的概率分析，建立模型的普适性结果，拓宽对财富分配动力学的理解

- 结论性质：提供一套新颖且更一般的证明方法，补充和部分超越此前基于鞅性质的经典结果。

---

2. 逐节深度解读

2.1 引言与模型综述（页0-1）

• 摘要简介：

- Chakraborti的yard-sale模型中，$N$个代理人两两交易，每次交易基于较贫者的财富和硬币翻转决定财富流向且期望财富守恒。
- 传统认知基于Doob鞅收敛定理推导，最终财富“凝聚”进入单一代理人，且比例等于其初始拥有概率。
- 若交易对受限（不完整图），则产生局部财富凝聚：多数代理贫困，少数非邻接代理富裕。
- 当前论文拟以更初等且适用范围更广的新方法来证明此现象，并涉及带偏向的交易概率情况。

• 关键模型定义：

- $X\ell^i$ 表示第$\ell$交易后代理$i$所占经济体总财富比重，满足$\sumi X\ell^i=1$。
- 交易对$(i\ell,j\ell)$随机选取，确定二者中较贫者记为$\mu\ell$，较富者为$\mathbf{v}\ell$。
- 资金流动取决于财富比例$b \in (0,1)$，以及$s\ell \in \{-1,1\}$的公平二项随机变量。

• 博弈机制简述：

- 交易时，较贫者财富的$b$比例依据$s\ell$方向移动，且这种交换保持期望财富不变，但造成财富随机波动。

• 重点：

- 模型中的随机交易即使无偏（公平抛币），依然导致极端财富不均（财富凝聚）。
- 传统证明依赖于代理财富比重为鞅过程，收敛到基向量。
- 讨论扩展存在于交易网络受限与财富偏向交易的情形，后者使得$X{\ell}^{i}$不再满足鞅条件，需新工具。\[[page::0,1]\]

2.2 局部财富凝聚与交易网络（页2）

• 图1说明：

- 展示了基于不完整交易网络的yard-sale模拟结果，多幅图对比下财富集中于多个非邻接节点，表明财富凝聚局部化。
- 点大小表示最终财富大小，富裕节点间无直接交易连接，暗示财富不流动聚集在少量“孤立”节点。

• 模型更细致设定：

- 建立严格的随机过程数学框架，包含：
- 代理数$N$，初始财富向量$X0$
- 带有0/1元素的邻接矩阵$A$表示可交易边，$a{ij}=1$意味着$i$和$j$可交易。
- 交易对$(i\ell,j\ell)$依概率分布$\pi$独立生成。
- 交易中的财富比例$b\ell$和倾向概率$p\ell$允许依赖于历史财富路径并且带随机性（通过均匀$U\ell, V\ell$注入）。

• 模型表达：

- 用可测函数$f\ell,g\ell$表征财富比例$b\ell$和偏向概率$p\ell$的生成
- 交易结果调整财富：$X\ell^{\mu\ell} = X{\ell-1}^{\mu\ell} - s\ell B\ell X{\ell-1}^{\mu\ell}$，$\quad X\ell^{v\ell}=X{\ell-1}^{v\ell} + s\ell B\ell X{\ell-1}^{\mu\ell}$

• 意义：

- 该设置相较以往简化的固定$b$和$p=0.5$模型，更灵活包含风险偏好变化、交易偏向（如财富优势$ p\ell > 0.5$ 或贫困优势$ p\ell < 0.5$）等机制，为后续分析奠定基础。\[[page::2,3]\]

2.3 欧几里得范数变化的条件期望（页3-4）

• 数学关键环节：

- 聚焦于财富分布向量$X\ell$的$\ell^2$-范数（即$L^2$范数），数学表达为$\|X\ell\|^2 = \sum{i=1}^N (X\ell^i)^2$。
- 该范数衡量财富集中程度，越接近1表示越集中（单个代理财富占比接近1）。

• 命题与推导：

- 计算单步交易中$\|X\ell\|^2$与$\|X{\ell-1}\|^2$的条件期望差值，根据定义，公式（6）：

$$
E\left(\|X\ell\|^2 - \|X{\ell-1}\|^2 | \text{条件}\right) = (4p\ell - 2) B\ell X{\ell-1}^{\mu\ell}(X{\ell-1}^{v\ell} - X{\ell-1}^{\mu\ell}) + 2 (B\ell X{\ell-1}^{\mu\ell})^2.
$$

• 结论：

- 对于公平硬币（$p\ell=1/2$），左边第一项消失，变动总是正，意味着$L^2$范数以某种非负期望增长，财富集中度倾向上升。
- 对于财富优势（$p\ell > 1/2$），该增长趋势更明显。
- 对于贫困优势（$p\ell < 1/2$），给出不等式（7）作为条件保证第二项大幅补偿，依然保证期望非负以支持财富凝聚。

• 数学形式与逻辑：

- 变动的拆分清晰体现了交易倾向（概率偏差）对财富集中度演化的影响，并提出条件(7)：

$$
(4p\ell - 2)(X{\ell-1}^{v\ell} - X{\ell-1}^{\mu\ell}) \geq -8 X{\ell-1}^{\mu\ell} \quad \text{a.s.}
$$

保证期望收益非负。

• 重要性：

- 此推导直接展现了财富集中度的单调趋势更新核心动力，突破传统依赖鞅性质的限制，能适用更广泛的偏向交易模型。\[[page::3,4]\]

2.4 收敛与财富比例趋零（页4）

• 引理2重点：

- 证明$\lim{\ell\to \infty} X{\ell-1}^{\mu\ell} = 0$几乎必然成立，说明被交易中较贫者财富逐步缩减。

• 证明思路：

- 利用Borel-Cantelli引理，通过期望上的平方和收敛性推导发生超过某阈值的事件只有有限次，故财富比例必趋零。
- 关键计算：

$$
\sum{\ell=1}^\infty E\left( (B\ell X{\ell-1}^{\mu\ell})^2 \right) \leq 1,
$$

确保概率事件逐渐消失。

• 经济含义：

- 逐次交易中“较贫者”在频繁交易中财富比例被压缩，表明财富差距加剧的不对称性动态。\[[page::4]\]

2.5 局部财富凝聚定理及其意义（页5）

• 定义：

- 集合$\mathcal{C}$表示“局部财富凝聚”的财富分布，任一两个相连代理人不会同时拥有正财富，即资源分配相邻节点中只有一个或无财富者。

• 定理2(广义Yard-Sale收敛定理)：

- 在条件(7)假设成立下，财富序列$X\ell$以任一范数距离收敛至集合$\mathcal{C}$。

• 证明关键：

- 若不成立，则存在正概率有较大财富比例存在于任意交易边相连的节点对中，矛盾于上一引理中较贫者财富必趋零的结论。

• 经济解读：

- 交易网络的局部结构直接影响财富分布的空间分布，非完整网络促使财富在非交易邻居节点间局部集中，形成多富裕点而非全局璧合。

• 图表联系：

- 该理论对应图1中模拟的财富分布结果，解释为何富裕节点不直接交易且财富差距固定。\[[page::5]\]

2.6 讨论与研究边界（页5-6）

• 核心观点：

- 纯随机、统计无偏差的交易行为即可导致极端的财富不均，非富即贫，弱化了能力或勤奋的必要性。
- 文中方法在保持清晰和通用性间做权衡，允许历史依赖性但要求交易对概率下界非零。
- 数值和启发式研究表明贫困优势极轻微偏差下依然可能发生财富凝聚，但本定理条件不适用，显示本结果的局限。
- 对完全图而言，收敛点为孤立的基向量（单一富裕代理）；不完整图中$\mathcal{C}$含非孤立点，收敛状态不唯一，行为复杂。

• 结论：

- 本文提出的概率分析方法为有限代理人yard-sale模型提供了迄今为止最简单且最通用的严格数学证明工具。

---

3. 图表深度解读

图1（页2）

• 描述：

- 三幅同构不完整网络上的财富分布模拟，灰色点大小表示代理财富大小。
- 左图有两富裕节点，中间图三富裕节点，右图四富裕节点。
- 富裕节点之间无直接交易边相连，体现财富相互独立积累。

• 数据趋势与含义：

- 网络约束导致财富分散至多个独立子群体，不同于完全图上的单一财富集中。
- 富裕代理通过网络断层隔离，避免财富重新分配。
- 富裕节点数目与网络结构相关，反映局部财富凝聚的复杂性和多样性。

• 理论联系：

- 图示直观展示了定理2涉及的集合$\mathcal{C}$的基本性质：财富在邻接节点中交替出现零与正值的格局。

• 限制与注释：

- 模拟为数值实验，不代表所有随机化结果，但为理论结果提供形象支持和启发。



---

4. 估值与数学方法分析

• 模型核心方法：

- 运用财富分布向量的$L^2$范数作为集中度的度量指标，提供量化分析工具。
- 计算单步交易中财富分布的$L^2$增长，结合交易偏向概率$p\ell$和财富比例$b\ell$判断集中趋势。

• 与传统鞅理论的区别：

- 传统证明依赖于$X\ell^i$为鞅过程，适用于无偏或者公平硬币模型。
- 新方法突破了这一限制，以更广泛的条件保证期望的单步增益，适配财富依赖偏差，扩展理论适用广度。

• 关键量化不等式：

$$
E\left(\|X\ell\|^2 - \|X{\ell-1}\|^2 | \text{条件}\right) \geq (B\ell X{\ell-1}^{\mu\ell})^2,
$$

是理论基础，确保财富分布浓缩度在动态中不会萎缩，从而驱动凝聚。

• 敏感性与限制：

- 条件(7)为理论依赖，若极端贫困优势（小于1/2）轻微偏离不满足，当前方法未覆盖该场景。
- 交易对概率需有正下界，避免某些代理完全退出交易过程。

---

5. 风险因素评估

• 模型风险来源：

- 交易偏向概率的不确定性（$p\ell$不是固定或波动范围不符条件）。
- 交易对概率分布$\pi$不均或依赖历史导致模型退化。
- 贫困优势轻微偏离条件(7)导致方法失效，无法保证财富凝聚的结论。

• 缓解策略与说明：

- 论文建议中针对交易选择的概率分布保持正下界，避免出现“死角”代理。
- 讨论将模型扩展至更松散限制，但以牺牲证明简洁性换取更广泛适用。

• 研究限制：

- 模型假设中人口固定，未涵盖代理人动态进入或退出。
- 贫穷优势极端情况仍需新的数学工具解析。

---

6. 审慎视角与细微差别

• 客观观察：

- 本文虽为数学证明贡献，坚守条件较为严格，尤其是假设(7)对贫困优势的把控仍有局限。
- 交易对选择须满足正概率下界，现实网络中交易边可能随时间变化，该假设理想化明显。
- 收敛至集合$\mathcal{C}$只保证距离趋零，不保证单点收敛（特别是不完整图），后者有更强的推断难度。

• 潜在偏见与诠释：

- 作者强调本方法“最简单且最通用”的断言，是相对当前文献而言，仍留待进一步挑战。
- 对贫困优势临界情况的数值模拟引用表明理论与现实复杂经济行为间仍存差距。

• 模型与现实的契合度问题：

- 模型代理人完全同质，未考虑能力和策略差异，忽略宏观经济波动影响。

---

7. 结论性综合

本文针对Chakraborti提出的yard-sale财富交换模型，以概率论工具重新审视财富凝聚现象。在经典基于Doob鞅收敛定理的证明确立财富向单一代理聚集的基础上，本文创新性地使用财富分布的$L^2$范数作为集中度指标，对财富动态的单步条件期望变动展开分析，进而提出条件(7)确保财富集中度在交易历程中不减，进而证明局部财富凝聚。

通过引入交易网络结构（不完全图），结果体现为多富裕子群形成，财富集中于非邻接节点，即局部财富凝聚现象，模拟图1形象展示了这种现象。文中严格数学推导覆盖了传统公正硬币投掷情形，亦适用于财富优势（$p_\ell > 0.5$）及部分贫困优势情形，拓宽了模型适用性。

文章系统阐述了模型设定、概率环境、交易机制与财富分配的动态关系，定量分析单步财富集中度改变，使用Borel-Cantelli引理证明关键财富比例趋零，最终由此保证财富向局部凝聚集合$\mathcal{C}$收敛。

尽管存在贫困优势轻微偏差不满足假设的限制及交易概率分布的理想化假设，但本文提出的数学方法为理解财富分配不平等生成机制提供了极具参考价值的理论框架和创新工具，填补了现有文献中关于偏向交易模型严谨证明的空白。

综上，本报告全面揭示了该文献从模型设定、理论推导到数值验证的逻辑链条，清晰解读了各种假设和定理背后的经济与数学含义，强调新证明框架在财富动态研究中的理论重要性，提升了对财富凝聚现象数学本质的认知。其对经济学、统计物理及复杂网络领域均有重要启示意义。[page::0,1,2,3,4,5,6]

---

参考文献

论文原文附录[6页]含完整文献清单。主要参考文献囊括了yard-sale早期模型[6]、基于鞅的经典证明[7]、局部凝聚网络研究[4,11]、偏向优势分析[1,12]及财富不平等量化工具[5]等，为该文贡献提供了坚实学术支持。

报告