• 研究目标与背景 [page::0][page::1]

- 去中心化金融DeFi旨在通过区块链智能合约替代传统金融中介。
- 流动性提供者（LP）通过持有AMM发行的流动性代币参与市场，目前定价机制存显著套利机会。
- 现有流动性代币的定价多基于过时理论，缺乏对冲策略，导致近半数LP亏损。

• CPMM机制与流动性代币价值基础 [page::3][page::4]

- CPMM定义为二资产的恒定乘积函数u(x,y)=xy；流动性代币数量定义为L=√(xy)。
- 流动性代币价值与价格P和流动性L一一对应，价值公式为2L√P。
- 对流动性代币可通过持有基础资产进行Delta对冲，Delta=1/√P。

• 市场数据中的套利实证分析（Example 2.3） [page::5][page::6]

- 以Polygon链Uniswap USDC/WETH池为例，手续费5bps，区块间隔2秒，风险利率5%。
- 通过二次对冲展示Delta对冲组合存在显著的正趋势，表明套利机会存在。



- 不同利率条件均未消除套利，利率越低套利越明显，最低套利出现在0%利率时。

• 风险中性定价模型与对冲希腊字母分析 [page::7][page::8][page::9][page::13][page::14]

- 价格过程假设为风险中性几何布朗运动，流动性代币视为永久Bermudan期权，伴随费用流。
- 定义价值函数满足动态规划，建立风险中性定价定理，关键判据为手续费调整因子$\hat{\gamma}$是否超过阈值$\hat{\gamma}^$。
- 流动性代币价值公式：$V_0(P) = \frac{2\hat{\gamma}\sqrt{P}}{\hat{\gamma}^}$，当且仅当$\hat{\gamma} \geq \hat{\gamma}^*$。
- 重要希腊字母指标：
- Delta正值且随价格P的平方根逆相关；
- Gamma为负，表明价格曲线凹性；
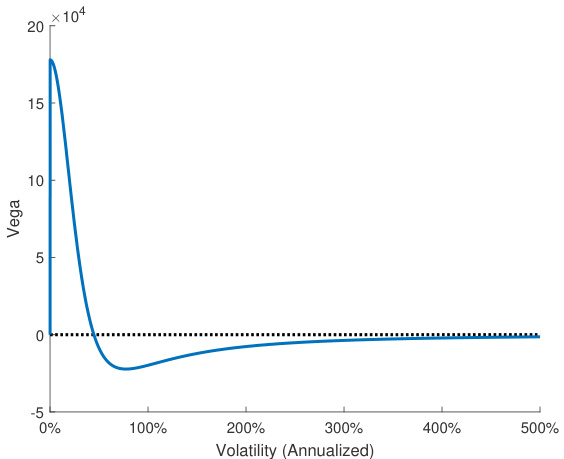
- Vega对波动率依赖非单调，小波动率时为正，大波动率时为负。


- 该关系揭示流动性代币复杂的波动率敏感性，区别于传统欧式期权。

• 隐含波动率分析与套利机会识别 [page::15][page::16][page::17][page::18]

- 定义隐含波动率为使风险中性价等于现行市场价$2\sqrt{P}$的波动率。
- 存在三种情形：无解、唯一解及双重解，具体取决于手续费率$\gamma$、区块间隔$\Delta t$和风险利率$r$。
- Polygon链标准参数下，当手续费5bps时存在两个隐含波动率，价格存在明显套利区间。

• 市场数据校准的无套利隐含波动率与重新定价 [page::19][page::20][page::22][page::23]

- 利用实际Uniswap USDC/WETH池数据构造损益函数，解出市场校准波动率$\sigma^M\approx25.82\%$。
- 校准结果表明当前市场以5bps费率显著低估流动性代币价值（低估因子约3倍）。
- 重新定价下的Delta对冲组合波动较小，近似无套利。

• 提出两种新型AMM设计框架以消除套利及实现动态定价 [page::24][page::25]

- 可变铸造/销毁成本定价：引入流动性代币价格依赖于流动性总量函数$v(L)$实现价格随市场变化浮动，函数条件保证价格合理变化。
- 可变手续费率定价：手续费率$\gamma(L)$随流动性调整，能更有效支持可变价格但投资者需动态评估手续费变化风险。
- 两种设计旨在突破当前恒定$2\sqrt{P}$定价盲区，实现更合理的风险中性定价。

• 结论与未来方向 [page::25][page::26]

- 当前CPMM流动性代币定价存在显著套利，报告提出的风险中性定价理论及校准方法实现了无套利重新定价。
- 拟议的动态定价设计为未来去中心化交易所及AMM智能合约设计提供新思路。
- 未来研究将聚焦集中流动性AMM等更复杂产品的风险中性定价及流动性风险管理。

DeFi Arbitrage in Hedged Liquidity Tokens — 详尽分析报告

---

1. 元数据与概览

标题：DeFi Arbitrage in Hedged Liquidity Tokens
作者：Maxim Bichuch, Zachary Feinstein
日期：2024年12月30日
机构：未明示，基于学术论文格式，理论研究性质明显
主题：去中心化金融（DeFi）中的流动性代币定价与套利，特别聚焦于基于恒定乘积市场制造商（CPMM，例：Uniswap）机制的自动化做市商（AMM）中的流动性代币风险中性定价与套保策略。

核心论点概述：

• 当前市场对CPMM流动性代币的定价存在可被套保套利的空间，这表明流动性代币价格未有效反映风险。

- 作者将流动性代币视为基于标的资产价格的路径依赖衍生品，推导了其风险中性定价和套保公式，类似于Black–Scholes框架。

• 通过这种风险中性定价方法，作者提出了一种隐含波动率标定方法，校正流动性代币价格达到无套利状态。

- 论文提出了若干新型AMM设计方案，旨在实现流动性代币价格机制的现代化，消除套利可能。

总体来看，作者通过理论与实证结合，突破传统CPMM价格模型，强调金融衍生品定价思路在DeFi领域的应用和发展需求。[page::0,1,2]

---

2. 逐节深度解读

2.1 引言与研究动机

• DeFi利用智能合约替代传统金融中介，允许投资者作为LP为资产池提供流动性。

- 以Uniswap等CPMM为代表的AMM通过智能合约实现分散交易，LP通过提供双资产获得代表其贡献的流动性代币。

• 作者创新地将流动性代币视为路径依赖的永久衍生品，获取手续费作为红利流（dividend），本质上是一种衍生品投资。

- 实证发现现有CPMM流动性代币报价存在明显套利机会，且近半数LP亏损，强调迫切需要风险中性定价与套保理论支持。

本节厘清了研究定位与现存问题，为后续理论框架构建奠基。[page::0,1]

2.2 相关文献与研究差异

• 文献多将流动性代币近似为期权性质，但未将其价格及波动率视作内生量系统性研究。

- 作者提出以波动率匹配价格的隐含波动率定标方法，首次对流动性代币的希腊字母（Greeks）进行系统探讨。

• 本文聚焦于基于手续费流的价值驱动，而非资产池标的资产本身，这种定位区分了现有文献。

通过理论细致差异化指出本研究创新点，突出系统性风险中性框架的独特贡献。[page::1]

2.3 研究贡献与论文结构

• 贡献一：将流动性代币建模为基于底层资产价格的衍生品，求解最优买卖（阻止）策略。

- 贡献二：基于最优执行，给出风险中性定价公式，首次系统构造流动性代币的希腊字母和套保策略。

• 贡献三：理论与Uniswap实际数据结合，发现现有定价存在套利，利用隐含波动率方法校正，得到无套利价格。

此外，篇幅结构清晰，逻辑连贯，分别从理论模型、实证分析、定价校准、设计改进等方面展开。[page::2]

---

3. AMM与CPMM基础

3.1 AMM定义

• AMM是资产池集合，交易者能直接与池子交互。

- 其中价格映射由效用函数定义，CFMM（Constant Function Market Maker，恒定函数做市商）确保交易前后效用保持不变。

• 具体的CPMM为二维资产池，效用函数形式为 \( u(x,y) = xy \) ，代表Uniswap等平台的主流实现。

- 定价oracle由偏导数确定资产边际价格比率，理论上无手续费，实际中引入手续费参数 \(\gamma\) 抽取部分成交资产。

• LP通过等价价值入池，持有流动性代币，提现时按份额提取底层资产与手续费分配比例。

- 区块链交易发生在离散区块时间，交易价格观测基于区块时间间隔 \(\Delta t\)，本文以此为假定，简化模型分析。

梳理AMM特别是CPMM数学框架，凸显智能合约和链上机制影响，给后续量化模型提供基础。[page::3,4]

3.2 流动性代币的价格与套保

• CPMM中，流动性代币的数量定义为 \(L = \sqrt{xy}\)，资产池中的资产 \(x,y\) 可由当前价格 \(P\) 与 \(L\) 反推： \( x = L / \sqrt{P}, y = L \sqrt{P} \)。

- 流动性代币价值表示为 \(2 L \sqrt{P}\)，即两倍的流动性平方根估值。

• 该流动性代币风险可通过对底层资产仓位按敏感度（Delta）动态对冲， 公式为 \(\Delta = \frac{d}{dP} 2\sqrt{P} = \frac{1}{\sqrt{P}}\)。

- 实证基于Uniswap v3上的USDC/WETH池，2秒区块时间，5bps手续费，数据显示持有单个流动性代币与其对应的Delta套保头寸相比，套保头寸波动明显降低，但却展现出正向趋势，暗示出现套利机会。

• 不同风险无风险利率（0%-50%）均存在套利，表明套利并非利率设定偏差的假象，而是价格机制固有缺陷。

这说明当前流动性代币市场价格定价存在结构性套利缺陷，强调改进空间。[page::4,5]

---

4. 定价模型及风险中性估值

4.1 市场模型假设

• 价格过程 \(Pt\) 假设遵循风险中性测度下的几何布朗运动（GBM）：

\[
dPt = Pt (r dt + \sigma dWt)
\]

• 价格可在链外连续交易，链上仅在离散区块时间 \(\Delta t\) 可交易。

- 合约假设每个区块仅有一笔交易，确保价格恰好对齐，简化套保估计。

该模型承接传统金融，应用于链上DeFi的时间离散及手续费结构，体现风险中性测度下衍生品估值标准。[page::7,8]

4.2 风险中性定价公式详解

• 流动性代币被建模为可在任一区块时刻行使的长期Bermudan期权。

- 价钱函数:
\[
V0(P) = \max \left\{ 2\sqrt{P}, \, e^{-r\Delta t} \mathbb{E}[ V0(P{next}) + \hat{\gamma} F(P, P{next}) ] \right\}
\]

• 其中手续费函数 \(F\) 定义资产池变动比例的手续费金额，\(\hat{\gamma} = \frac{\gamma}{1-\gamma}\) 表示LP在手续费中所占份额。

- 重要定理（3.2）指出，只有当手续费比例 \(\hat{\gamma} \geq \hat{\gamma}^\) 时，LP才会持续投资该池且流动性代币的价值为：
\[
V0(P0) = \frac{2 \hat{\gamma} \sqrt{P0}}{\hat{\gamma}^}
\]

• \(\hat{\gamma}^\)由区块时间长度、风险利率、波动率及标准正态累积分布函数综合确定（详细公式见正文）。

- 证明利用了期望计算与动态规划原理，验证持续持仓与随时取款的价值对比，严格建立了该衍生品的风险中性恒等价关系。

• 还有非区块时间点的价值计算（Corollary 3.3），强调因链上交易离散性，代币在链外连续时间内价差表现。

阐明了流动性代币的风险中性内在价值，直接指出市场定价中套利根源与优化空间。[page::8-12]

4.3 流动性代币的希腊字母（Greeks）

• Delta（对价格变动敏感度）：

\[
\frac{\partial}{\partial P} V0(P) = \frac{\hat{\gamma}}{\hat{\gamma}^ \sqrt{P}} = \frac{V0(P)}{2P} > 0
\]

• Gamma（Delta相对于价格的弯曲度）：

\[
\frac{\partial^2}{\partial P^2} V0(P) = - \frac{\hat{\gamma}}{2 \hat{\gamma}^* P^{3/2}} < 0
\]

• Vega（对价格波动率的敏感度）结构复杂：

Vega不是单调正值，呈现非线性，波动率较小时Vega正，波动率极大时Vega负，原因在于小波动率增加时交易频率提升手续费，波动极大时价格崩溃概率增大使代币价值下滑。

• 图示（图3）展示token价值和Vega相对年化波动率取值的非线性关系，强调风险管理中波动率参数选择的重要性。

该节首次系统推导CPMM流动性代币的风险管理工具，丰富了DeFi金融产品理论。[page::13,14]

---

5. 隐含波动率与无套利定价校准

5.1 隐含波动率定义及性质

• “隐含波动率”定义为使风险中性价值 \(V0(P) = 2\sqrt{P}\) 的波动率 \(\sigma\)，即市场价格与风险中性估值一致的波动率。

- 研究发现隐含波动率存在三种情况：
1. 不存在隐含波动率
2. 唯一隐含波动率
3. 两个隐含波动率

• 该现象与Vega对波动率的非单调特征相映照。

- 不同风险无风险利率 \(r=0\) 和 \(r>0\) 情况下，存在门限条件区分是否存在隐含波动率。

该分析为理解市场价格和风险中性模型价差提供理论因由。[page::15,16]

5.2 市场套利条件

• 明确指出市场上是否存在套利机会取决于是否符合 \(\sigma < \sigma^I\) （波动率小于隐含波动率）等条件。

- 结合手续费率 \(\gamma\) 与区块时间 \(\Delta t\)，阐明费率足够高且波动率处于区间时，存在套利空间。

• 图4说明在Polygon链不同费率场景下隐含波动率的变化与套利区域，具体参数点对应案例。

为理解市场实际运行机制中套利出现的动态条件与结构提供清晰准则。[page::17,18]

5.3 无套利价格的实证校准

• 研究以实测Uniswap USDC/WETH池数据为例，构造实际交易手续费流及价格序列，基于前述理论进行波动率标定。

- 解方程确定校准波动率 \(\sigma^M\)，使估值满足无套利马尔科夫定价。

• 结果显示校准波动率约为25.82%（年化），远离隐含波动率区间，提示原市场定价低估了流动性代币价值。

- 校准后流动性代币价格比原价格高出约3倍，表明现有定价严重低估投资风险收益。

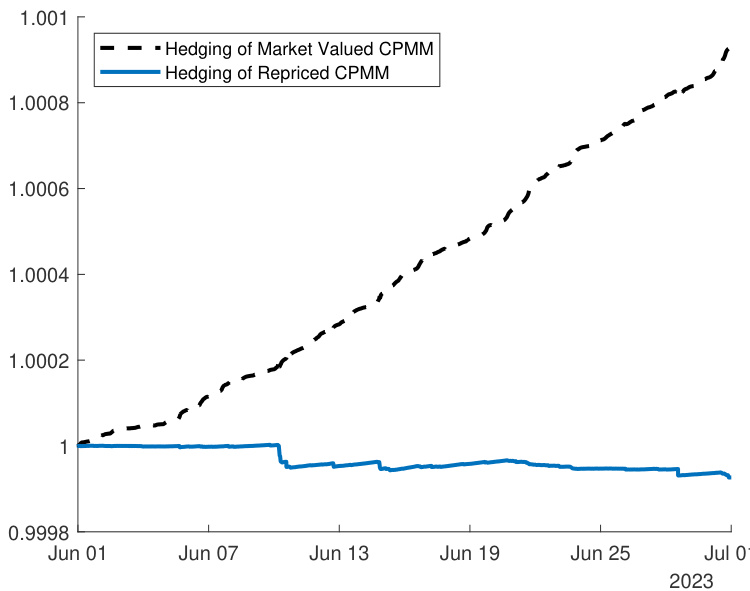
• 图5直观显示了重新定价后delta套保头寸的持平效果，较原市场价格的套保头寸走势呈现明显优势。

该实证支持理论模型实用性，并展示了如何从链上实际数据进行金融工程校正，为投资者与平台提供决策依据。[page::19-23]

---

6. 新型AMM设计建议

• 鉴于现有CPMM价格结构固定为 \(2\sqrt{P}\) ，导致流动性代币价格缺乏自由浮动，套利机会难以消除。

- 提出两类可实现流动性代币定价动态浮动的设计方案：

1. 流动性代币铸造/销毁成本依赖总流动性 \(L\)
- 定价函数设为 \(V(P,L) = 2 v(L) \sqrt{P}\)，其中 \(v(\cdot)\) 是单调递增函数。
- 例如，令 \( \ell(L) = L^{2\alpha}, \alpha > 1 \)，则定价权重 \(v(L) = \alpha L^{\alpha-1}\)。
- 这种方法使代币价格除受当前资产价格外，还随市场整体流动性动态变化。
- 然而，由于存在多个CPMM设计的价格竞争，若无统一市场机制，投资者难以接受价格高于传统 \(2\sqrt{P}\)。

2. 手续费率 \(\gamma\) 作为流动性函数 \(\gamma(L)\)
- 费率随着总流动性水平下降，例如指数或反比例函数，使手续费随流动性自动调节。
- 进而风险中性估值随费率自动调整，从而影响代币价格，对套利及流动性引入自我调节机制。
- 这种设计使LP无法在初始时锁定手续费水平，需要动态管理持仓，对投资者监控和模型复杂度提出更高要求。

两种方案的提出旨在理论上克服流动性代币定价固化问题。尽管当前无实际市场实践，理论探讨为未来DeFi协议升级提供方向。[page::24,25]

---

7. 结论总结

• 实证和理论均证实现行CPMM流动性代币定价机制存在结构性套利，近似于“预Black–Scholes”时代的定价方法。

- 提出基于风险中性测度的流动性代币定价及套保理论，系统构造代币价值与希腊字母，助力风险管控。

• 通过实证校准，得到无套利价格并显著量化原市场定价低估程度，提供可操作的修正方法。

- 设计框架为AMM流动性代币定价机制提供了革命性改革思路，包括币种价格与流动性双变量动态定价和费率调整机制。

• 展望更复杂AMM设计（如Uniswap v3集中流动性）领域，预见流动性代币将具备DeFi隐含波动率曲线特征，研究价值巨大。

- 文末强调理论推进需实践验证，建议未来部署动态定价AMM合约以进一步考察理论适用性。

总结，本文突破了传统CPMM简单定价范式，奠定了DeFi金融衍生品定价现代化的基础。[page::25,26]

---

8. 重要图表详解

图1（第6页）

• 描述：

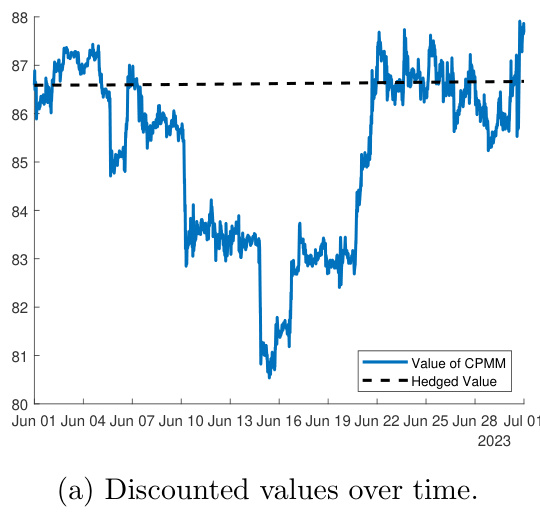
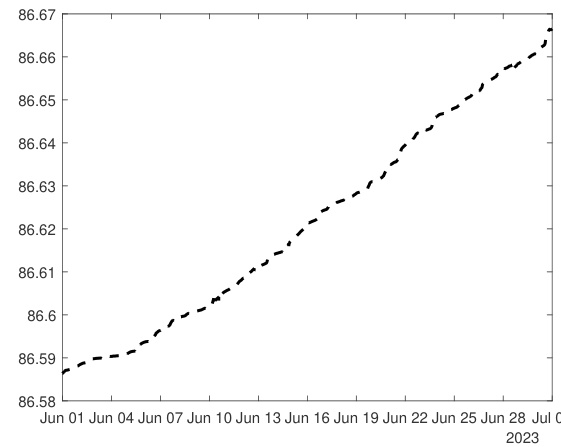
- 图1a展示2023年6月期间，一个流动性代币（基于当前价格与手续费的价值）及其Delta套保头寸的贴现价值随时间变化曲线。
- 图1b为图1a中Delta套保头寸贴现价值的局部放大图。

• 解读：

- 流动性代币价值波动明显大于Delta套保头寸，套保策略有效降低风险指标。
- 但Delta套保曲线呈现稳步上升趋势，揭示套保策略下存在正向套利机会。

• 数据支持文本论断：

- 反映市场定价不合理导致套利空间，与理论定价模型形成鲜明对比。[page::6]

图2（第6页）

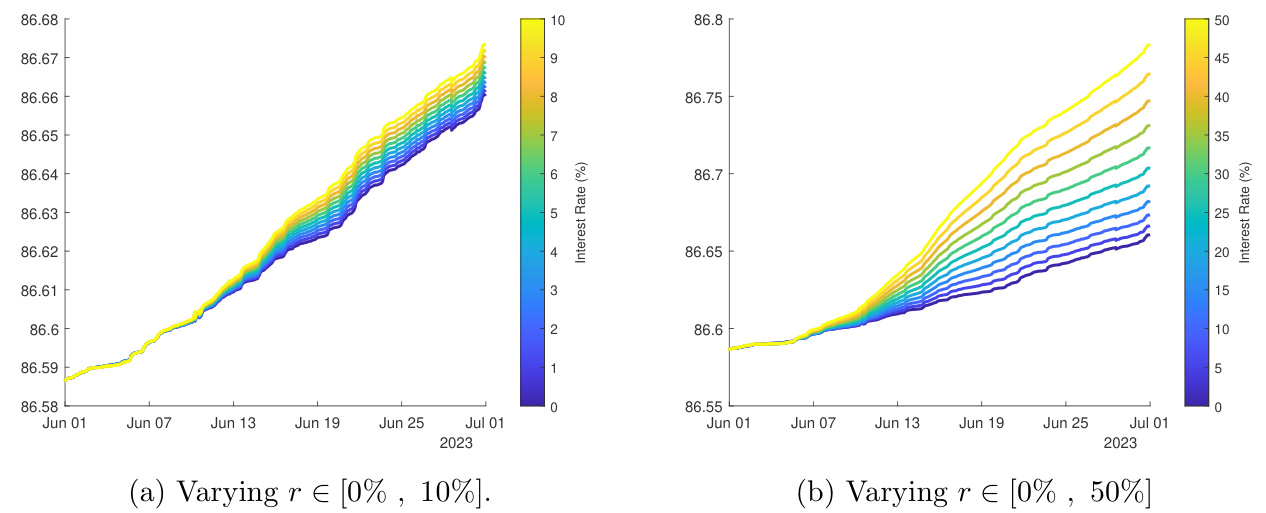
• 描述：

- 114小时内不同风险利率 \(r\) 设置下，Delta套保头寸贴现价值曲线叠加展示。
- 左图检视 \(r\) 从0%-10%，右图覆盖更大区间（0%-50%）。

• 解读：

- 不同无风险利率设置均存在类似正向套利趋势。
- 套利幅度随利率递增而减少，但即使为零利率，套利仍明显存在。

• 对比与支持：

- 证实套利机会不是利率假设的副作用，而是价格机制内生缺陷。[page::6]

图3（第14页）

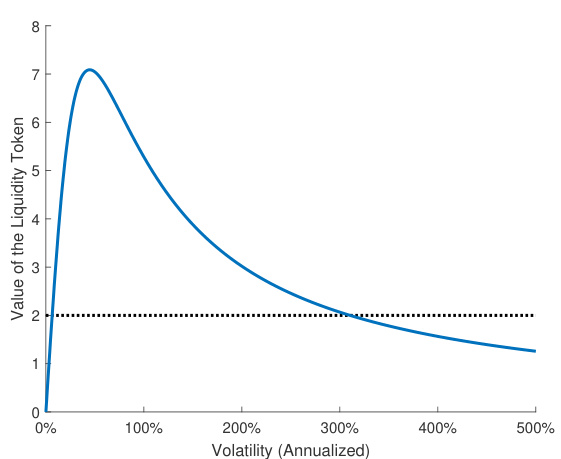
• 描述：

- (a) 展示流动性代币价值 \(V0(P_0)\) 作为年化波动率函数的变化；
- (b) Vega对波动率的非单调变化趋势。

• 解读：

- (a) 代币价值随波动率先上升后下降，峰值约在50%年化波动。
- (b) Vega正负交替，低波动率下Vega为正，高波动率下Vega为负，反映负面冲击风险。

• 联系理论：

- 解释了隐含波动率双重解现象，强化波动率对估值的复杂影响。[page::14]

图4（第18页）

• 描述：

- 标注不同手续费 \(\gamma\) 与波动率 \(\sigma\) 组合下套利区域和隐含波动率位点。

• 解读：

- 颜色填充区域显示套利可能存在的费率-波动率组合空间。
- 随手续费提高，允许的套利区间也扩展，存在单解和双解隐含波动率。

• 文本结合：

- 直观支持分段分析及案例验证，体现费率对市场定价及套利机会的关键影响。[page::18]

图5（第23页）

• 描述：

- 重新定价（校准波动率下）与原始市场价格下，Delta套保头寸的贴现价值对比。

• 解读：

- 校准后套保头寸价值稳定围绕1，波动极小。
- 原市场价的套保头寸持续上升，暗示套利存在。

• 论证效果：

- 验证校准波动率带来的价格近似无套利，提高模型适用性和实用性。[page::23]

---

9. 批判性视角与细节关注

• 本研究基于风险中性GBM假设，忽视了实际市场可能存在的跳跃、波动率微笑及流动性冲击，模型可能在极端行情下失准。

- 论文内假设手续费率为固定或依流水线性变化，但实际费率受多种链上经济激励及市场竞争影响，动态控制设计存在执行难度。

• 校准隐含波动率时依赖于区块链链上数据质量和频率，短期数据噪声可能影响准确性。

- 论文假设套保交易无摩擦且完全执行，实际由于链上交易延迟和成本，套保策略可能无法完美实现。

• 设计新型AMM的提案理论先进，但在实际DeFi生态中实施风险和系统复杂度尚未评估。

- 部分公式推导（尤其第9至10页）繁复且有排版问题，解读难度较高，后续应当优化表达。

篇幅较长的理论与实证融合论文，细节质量高但仍需进一步现实交易摩擦考量及实验验证。[page::9-12,24-26]

---

10. 结论性综合

本文针对去中心化金融AMM中的流动性代币，特别是基于CPMM机制的代币，系统建立风险中性定价与套保理论。作者创新地将流动性代币看作路径依赖的永久期权衍生品，通过风险中性测度，导出显式定价公式及希腊字母计算，极大提升了流动性代币风险管理的理论基础。

重要发现包括：实际市场价格 \(2\sqrt{P}\) 存在明显低估现象，套利机会触目惊心；以Uniswap上链数据为例，校准隐含波动率提供了切实可行的无套利价格体系，套利空间被有效缩小。多个关键图表直观展现了相关价格波动性、套利区间及再定价方案的优越性。

最终，作者提出了流动性代币定价机制革新的两种方案——基于总流动性调整代币定价与基于流动性动态调整手续费率，预示未来DeFi市场发展将趋向更加复杂和高效的价格竞争环境。

整体来看，本文突破DeFi资产定价传统预设，向现代金融衍生品理论看齐，建立了DeFi领域风险定价与套利检测的数学工具箱。对研究者与DeFi从业者均具高度价值，尤为适合结合链上数据应用于智能投资和协议设计。理论高度严谨，实证丰富且方法创新，虽有公式表达复杂等局限，仍是DeFi金融工程及风险管理领域极具参考意义的重要研究成果。[page::0-26]

---

附：图表展示

图1: 套保与未套保流动性代币贴现价值

(a)


(b)

图2: 不同无风险利率下的Delta套保价值

(a) 0%-10%区间


(b) 0%-50%区间

图3: 价值与Vega对波动率的反应

(a) 价值曲线


(b) Vega变化

图4: 费率-波动率套利区域与隐含波动率

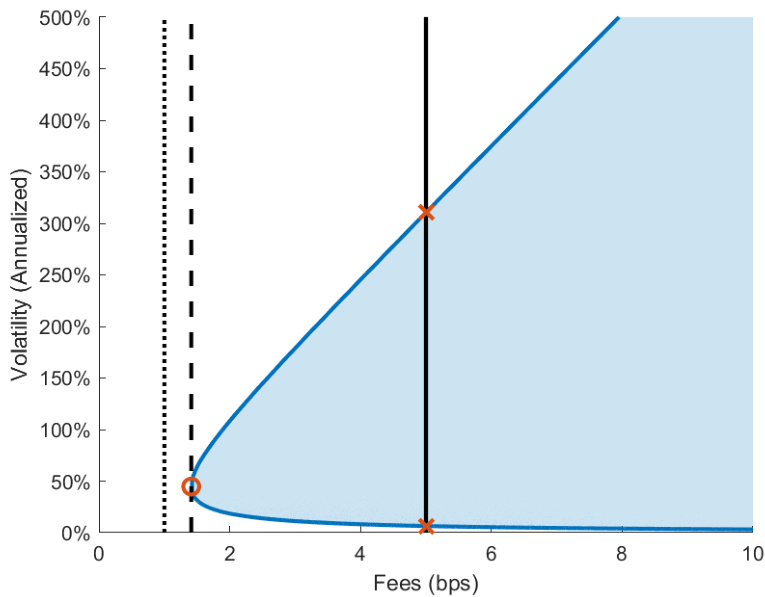
图5: 市场定价与校正定价下的Delta套保价值对比

---

总结

本文是DeFi领域极具前瞻性的金融工程研究，将复杂衍生品金融理论嫁接于区块链资产的流动性代币，深入剖析其内生定价缺陷及套利结构，结合数据校准与方案提案，推动AMM设计走向成熟和理论化。对DeFi流动性风险管理、智能合约设计及量化交易策略构建具有重要的启示和方法借鉴价值。

报告