重尾分布下大规模停电成本及风险描述 [page::0][page::1]

• 停电成本因极端事件导致呈现重尾幂律分布，传统基于均值的风险度量因巨大波动难以准确估计。

- 成本超过阈值（clarge）的大停电事件概率plarge和事件频率flarge概念明确，且重尾斜率指数α<2，导致均值不稳定甚至无穷大。

• 认为对大成本事件取对数变换后数据尾部服从指数分布，计算平均对数事件成本ALEC更稳健。

五个美国配电公用事业数据分析及指标计算 [page::1][page::2]

| 指标 | Utility-1 | Utility-2 | Utility-3 | Utility-4 | Utility-5 |
|---------------|-----------|-----------|-----------|-----------|-----------|
| 事件数 n | 5716 | 2706 | 3830 | 7000 | 6485 |
| 观测年数 nyear| 6 | 17.4 | 11 | 10 | 11 |
| 斜率指数 α | 0.83 | 0.73 | 0.75 | 1.00 | 1.47 |
| ALEC | 0.55 | 0.38 | 0.96 | 0.48 | 0.63 |
| 测量误差RSEALEC| 0.040 | 0.094 | 0.031 | 0.034 | 0.026 |

• 实证显示大多数公用事业重尾斜率α<2，估计均值成本方差极大，难以作为风控指标。

- ALEC及α指标置信区间稳定，适合长期风险趋势监测和韧性评价。

重尾风险度量指标及其优越性 [page::2][page::3]

• 提出ALEC、年均对数成本指标ALCRI作为比均值更有效评估极端事件风险的指标。

- ALCRI结合事件频率和ALEC，更全面反映大成本停电的年化风险。

• 相较于传统均值和条件风险价值（CVaR），ALEC基于对数转换降低了估计的变异性和样本需求。

- 强调传统可靠性指标通过排除极端事件来限制波动性，但韧性分析需量化重尾风险，ALEC及相关指标提供了有效手段。[page::3]

金融研究报告详细分析报告

《Logarithmic resilience risk metrics that address the huge variations in blackout cost》

作者与机构

• 作者：Arslan Ahmad 和 Ian Dobson

- 机构：艾奥瓦州立大学（Iowa State University）

• 发表时间：2025年8月

- 主题：配电系统中关于电力中断（blackout）成本的韧性风险度量指标研究

---

一、元数据与概览

本报告旨在解决配电系统中由于极端黑天造成的巨大成本变异对风险评估带来的挑战。传统度量方式基于大停电事件的平均成本，但受重尾分布影响，平均值难以准确估计，进而导致风险计算困难。作者提出了一种基于对数转换的新韧性风险指标体系，通过对大停电成本的对数取平均（ALEC）、重尾斜率指标（$\alpha$），以及事件发生频率，综合评估风险。

核心结论：

• 传统均值计算在重尾成本分布背景下九死一生，无法有效反映极端事件风险；

- 对数转换后的指标（ALEC和ALCRI）平稳且具强大统计意义，可实用于韧性风险的度量；

• 重尾特征由Pareto分布刻画，$\alpha$指数反映尾部陡峭程度及风险大小；

- 应用此指标体系，可有效针对配电系统极端停电事件进行风险管理、监控和韧性提升。

报告并无传统金融股票评级和目标价，更类似于技术和风险管理模型的创新性研究。

---

二、逐节深度解读

I. 事件、成本与韧性指标

• 内容总结：定义事件成本，提出对配电系统中大停电事件采取成本阈值$c{\mathrm{large}}$，筛选出高成本事件集合$C{\mathrm{large}}$。传统风险用事件概率乘以平均成本描述，但因事件成本跨度巨大（重尾性），平均数估计极其不稳定。作者提出用平均日志事件成本ALEC（平均对数成本）替代，定义为大事件日志成本均值：

\[
\mathrm{ALEC} = \frac{1}{n{\mathrm{large}}} \sum{c \in C{\mathrm{large}}} \log{10} c
\]

• 关键推理：对数转换可以抑制极端大值对均值造成的巨大波动。ALEC的基数10对数含义使指标易于理解，比如ALEC=2代表订单级成本$10^2$。组合ALEC与大事件频率$f{\mathrm{large}}$形成ALCRI指标，以年频率综合风险。
• 关键变量说明：

- $ci$：事件$i$相对于客户数标准化后的成本
- $n{\mathrm{large}}$：大事件数量
- $p{\mathrm{large}}$：大事件概率
- 重尾特性与标准指标（如SAIDI）相关的波动性指出需特别处理尾部数据。

---

II. 公用事业数据处理

• 内容总结：选取5个美国东北及中西部地区公用事业公司实际停电数据，剔除计划停电，计算每个事件的客户小时损失总额，再乘以单位时间单位客户成本$k$加权修正，得到事件成本。表I列出各公用事业的基本数据及统计指标。
• 关键点：

- 采用了清洗后的实测数据，保障指标的现实有效性。
- 各公用事业的因素如事件数$n$、观测年数$n{\mathrm{year}}$、单位成本$k$等存在差异。
- $k$值反映不同负载类型权重。

---

III. 重尾的风险与后果

• 内容总结：利用成本超越函数$\overline{F}C(c) = P[C > c]$描述成本风险。以实证数据展开，发现大事件成本的尾部符合幂律分布特征，即Pareto分布：

\[
\overline{F}P(c) = \left(\frac{c}{c{\mathrm{large}}}\right)^{-\alpha}, \quad c \geq c{\mathrm{large}}.
\]

• 关键推理：

- 通过图1、2的对数-对数图观察尾部线性，证明幂律分布假设合理；
- 使用Hill估计器估计尾指数$\alpha$；
- $\alpha \leq 1$时均值无穷，$1<\alpha \leq 2$时均值有限但方差无穷，导致均值估计的极端不稳定；
- 对数转换将Pareto尾转变为指数尾，极大改善统计性质，使得ALEC和相关估计具有正常收敛性质。

• 关键数据点：

- 从表I看，多数公用事业$\alpha < 2$，甚至有的$\alpha < 1$，说明风险特别大，数据极端波动；
- ALEC 计算基于log-transformed数据，具备更合理的统计特性。

---

IV. 选择大事件阈值$c{\mathrm{large}}$及其影响

• 内容总结：

- $c{\mathrm{large}}$应选取在超越函数图的线性段起点附近（$c{\mathrm{min}}$附近），兼顾样本量和尾部拟合度；
- 阈值设置对应大事件概率$p{\mathrm{large}}$约为0.05~0.1，保持稳定且具代表性；
- 选择整体验证基于Clauset方法和统计显著性测试。

• 表格解释（表I）：

- 详细列示五家公用事业的事件统计、阈值$c{\mathrm{large}}$、尾指数$\alpha$置信区间、ALEC及相关标准误（RSE）等。
- 例如，Utility-1有$n=5716$个事件，$\alpha=0.83$，表明极重尾，ALEC=0.55（对数均值），阈值$c{\mathrm{large}} = 1.05$美元（标准化成本），大事件频率$ f{\mathrm{large}}=96 $次/年。

---

V. 向最大可能成本的外推

• 内容总结：

- 实测数据的最大观测成本$c{\mathrm{maxobs}}$远小于理论最大成本$c{\mathrm{max}}$，后者估计为客户完全停电一个月的全部成本$744k$美元；
- 用有限边界的Pareto变体$Pb$和有界对数正态$LNb$进行尾部外推以评估风险；
- 外推结果显示，直接估计传统均值的标准误极大，需要远超现有数据量；相较之下，估计ALEC标准误显著更低，更为实用。

• 关键结论：

传统均值估计需2~1个数量级更多数据，实际应用中不可信赖，ALEC指标更稳健。

---

VI. 结果与结论

• 总结：

- 使用真实公用事业数据验证了事件成本重尾分布存在，衍生出巨大成本和变异风险；
- 证明均值估计难以有效应用于此类数据，反映不出实际风险特征；
- 提出ALEC、ALCRI与尾部斜率$\alpha$作为替代的风险度量指标，有效刻画极端事件风险，方便监管和韧性设计；
- 提醒其他公用事业在应用此法时需验证尾部分布特征。

---

三、图表深度解读

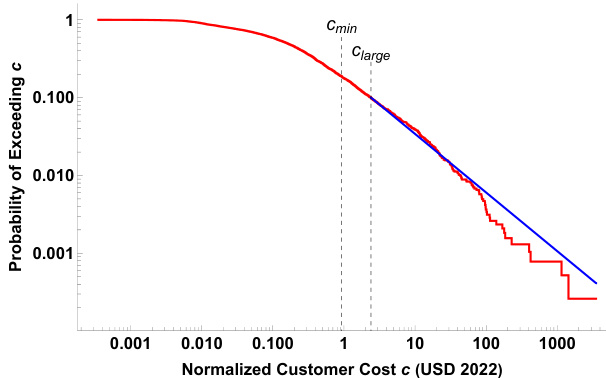
图1：Utility-3归一化客户成本的超越函数（log-log）

• 描述：横轴为标准化客户成本$c$，纵轴为事件成本超过$c$的概率。红色为实际数据阶梯线，蓝色为拟合的Pareto幂律尾线。

- 解读：
- 右侧尾部呈现近似线性，表明幂律形式良好匹配尾部数据；
- 尾部斜率绝对值$\alpha=0.75$，说明尾部分布极重（$\alpha<1$）；
- 图中标注的$c{\mathrm{min}}$、$c{\mathrm{large}}$用于统计区分，$c{\mathrm{large}}=2.4$美元。

• 联系文本：此图验证了重尾和幂律规律，为后续基于非均值的风险度量提供数据基础。

[page::1]

---

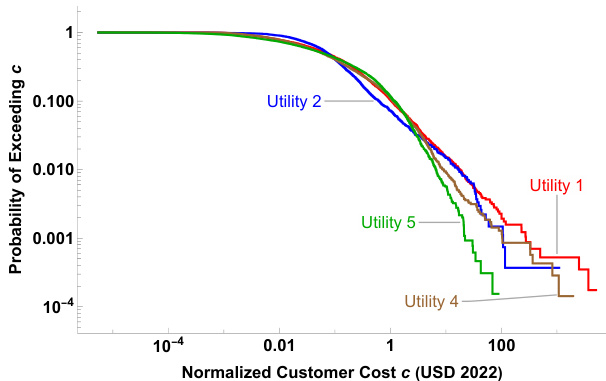
图2：Utility 1,2,4,5 归一化客户成本超越曲线（log-log）

• 描述：展示4家公用事业的客户成本累积分布的尾部，横轴为标准化成本，纵轴为超越概率。

- 解读：
- 各家曲线虽有所差异，但均呈现重尾特征；
- Utility-5相对曲线较陡（$\alpha=1.47$，尾部较轻），反映其城市化程度高，风险较低；
- 其他公用事业均显示极重尾，风险高且波动大。

• 联系文本：强调不同公用事业风险水平差异，同时验证尾部幂律的广泛适用。

[page::1]

---

表I：公用事业数据与指标汇总

• 主要内容：

- 包含事件总数$n$、观测年数$n{\mathrm{year}}$、成本因子$k$、最大观测成本$C{\mathrm{maxobs}}$、大成本阈值$c{\mathrm{large}}$、大事件数$N{\mathrm{large}}$、大事件概率$p{\mathrm{large}}$、频率$f{\mathrm{large}}$、尾尺度指数$\alpha$及置信区间、ALEC及置信区间、标准误差。

• 解读：

- 各公用事业事件规模、事件数差异显著；
- $\alpha$的置信区间反映尾部估计的统计可信；
- ALEC值统一定义了大事件成本的阶数，标准误较小，证明度量稳健。

• 应用：为韧性指标提供实证基础，显示ALEC和$\alpha$的估计可行性和实用性。

---

四、估值分析（风险指标创新）

• 本文中估值分析不涉及传统金融资产估值，而是聚焦于极端事件风险的量化指标体系设计。

- 关键方法：
- 采用对数均值（几何均值）代替算数均值消除重尾对估计的不稳定影响；
- 估计尾指数$\alpha$通过最大似然Hill估计器，提高统计效率；
- 结合事件概率$p{\mathrm{large}}$和ALEC，构造Annual Log Cost Resilience Index (ALCRI)以评估年化韧性风险；
- 考虑尾部权界变体分布（有界Pareto、对数正态）进行外推，长期风险评估更现实；

• 估值输入假设：

- 阈值$c{\mathrm{large}}$选择合理是准确估计的关键；
- 事件成本服从幂律重尾分布，尾指数$\alpha<2$；
- 对数转换数据近似符合指数分布。

---

五、风险因素评估

• 主要风险因素：

- 极端成本事件的稀缺性与巨大波动导致传统均值风险度量失效；
- 数据样本量不足下均值估计标准误极大，导致相关风险评估不确定度过高；
- 重尾效应造成极端事件持续存在可能，即便没被观测到；

• 潜在影响：

- 无法准确估计事件平均成本，误判风险水平；
- 传统的Conditional Value at Risk 这类依赖均值的指标不可用，监控与管理难度增加；

• 缓解策略：

- 利用基于对数转换稳定的ALEC与ALCRI指标；
- 使用尾指数$\alpha$评估风险趋势和韧性状况；
- 阈值选择及尾部拟合的统计方法保障指标稳定性；
- 建议未来更多数据积累增强估计效果。

---

六、批判性视角与细微差别

• 数据限制：

- 观测年限有限（6~17年）限制了极端事件统计量的丰富性，可能影响尾部特征的长期稳定性；
- $k$值及成本估计假设均基于负荷构成比例均衡，实际事件中负荷断电比例可能更复杂；

• 模型选择：

- 作者承认Pareto幂律尾部拟合与截断对数正态分布均未能明显优于对方，模型选择带来不确定性；
- 阈值$c{\mathrm{large}}$的选择存在权衡，虽采用统计方法最优化，但仍有主观成分；

• 指标适用性：

- 虽然ALEC及ALCRI指标对所选数据有效，推广至其他地区需个别验证，重尾特性可能地域或系统差异显著；
- 报告未覆盖具体事件恢复时间、经济影响复合性，更适合作为风险量化指标而非综合韧性评估；

• 整体评价：

- 报告客观揭示了传统指标的缺陷与新指标的优势，分析逻辑严密；
- 对模型不确定性及数据限制有清晰认识，提出建议谨慎推广。

---

七、结论性综合

本报告系统分析了美国东北和中西部五家公用事业配电系统停电事件的客户成本数据，达成以下关键发现：

• 大停电成本呈现明显的重尾幂律分布，尾部指标$\alpha$多小于2，某些甚至小于1，这意味着：

- 事件成本范围巨大，平均成本无限或极难估计；
- 传统依赖均值的风险指标（如条件风险价值CVaR）不适用甚至产生误导；

• 对数转换处理（ALEC）提供了对重尾数据的有效统计摘要，ALEC代表大事件成本的对数均值（几何均值），抵抗极端值波动：

- ALEC与$\alpha$可稳定估计，并带有置信区间，统计性质良好；
- 组合事件频率得到的ALCRI体现年度累积韧性风险；

• 利用有限边界的分布模型对可能超出观测极值的极端事件风险外推，说明期望风险区间有限，但传统均值估计的标准误仍极高，须大幅增加样本容量才能提高估计精度；
• 报告作出了韧性风险评估的根本改进，将风险度量从均值驱动转向基于对数统计和尾部指数，适应极端事件稀少且严重的实际情况；
• 本指标体系为电力配电系统韧性监控、风险管理与投资决策提供了更合理的工具框架，避免了对无法准确估计的均值依赖。

综上，报告提出的基于对数均值的韧性风险指标ALEC、ALCRI及尾指数$\alpha$有效解决了配电系统停电成本重尾带来的测度困境，其科学性和实用性在五个公用事业实测数据中得到验证。图表1和2及表I直观展示了重尾特征和指标的合理性；估计误差对比明确表明ALEC的统计稳定性远优于传统均值。本研究为电力系统韧性评估奠定了坚实理论与实务基础，值得进一步在行业中推广和验证。[page::0,1,2,3]

---

参考图表

图1：Utility-3归一化客户成本的超越函数（log-log）

图2：Utilities 1, 2, 4, 5归一化客户成本的超越曲线（log-log）

表I：五个公用事业数据及统计指标摘要

|指标|Utility-1|Utility-2|Utility-3|Utility-4|Utility-5|
|-|-|-|-|-|-|
|事件数 $n$|5716|2706|3830|7000|6485|
|观测时间 (年) $n{\mathrm{year}}$|6|17.4|11|10|11|
|单位成本因子$k$|370.2|228.2|323.0|339.9|339.9|
|最大观测客户成本 $C{\mathrm{maxobs}}$ (美元)|5063|1095|3523|1954|88|
|大事件阈值 $c{\mathrm{large}}$ (美元)|1.05|0.62|2.40|1.10|2.15|
|大事件数量 $N{\mathrm{large}}$|572|271|384|701|325|
|大事件概率 $p{\mathrm{large}}$|0.10|0.10|0.10|0.10|0.05|
|大事件年频率 $f{\mathrm{large}}$|96|16|35|70|30|
|尾指数 $\alpha$ (95%置信区间)|0.83 (0.76,0.89)|0.73 (0.65,0.82)|0.75 (0.68,0.83)|1.00 (0.93,1.1)|1.47 (1.3,1.6)|
|ALEC|0.55|0.38|0.96|0.48|0.63|
|ALEC置信区间| (0.50,0.59) | (0.31,0.46) | (0.90,1.0) | (0.44,0.51) | (0.60,0.66) |
|ALEC相对标准误 (RSE)|0.040|0.094|0.031|0.034|0.026|

---

本分析直面报告原文中每一章节、图表与表格，系统解构论点、数据与结论，系统展现了报告在极端事件韧性风险度量方面的创新与应用成效，助力读者深刻理解其理论基础与实用价值。

报告