• QFHS方法创新点及理论基础 [page::3][page::4][page::5][page::6]:

- QFHS结合分位数回归和历史模拟，通过估计的分位数序列对收益率进行规模调整，利用残差重采样实现多步VaR和ES预测。
- 泛化了传统的滤波历史模拟(FHS)，参数估计使用分位数损失函数而非高斯似然。
- 可以独立设定估计分位数$\alpha{est}$和目标风险水平$\alpha0$，极大增强了模型灵活性。

• 量化因子构建与策略框架 [page::5][page::6]:

- 利用CAViaR模型动态估计分位数；残差标准化后构建$\epsilon{\alpha,t} = rt / (-Q{\alpha,t})$，该序列为iid分布且分位数为-1。
- 通过bootstrap对$\epsilon{\alpha,t}$重采样，构建多步未来收益模拟路径，进而推断多步VaR和ES。

• 模拟研究主要发现 [page::7][page::8][page::9][page::12]:

- QFHS在峰度较高（低自由度t分布）和带偏态的数据生成过程中表现优于FHS，尤其是在$\alpha{est} \in [0.05, 0.15]$区间。
- 对于不同分布和估计水平，模型参数的相对标准误(rse)呈U型曲线，估计精度最低点对应的$\alpha$值通常明显高于目标风险水平，推荐估计分位数选择在0.05-0.15之间。

• 实证研究亮点及表格总结 [page::15][page::16][page::20][page::21]:

- 样本覆盖三个股指（SP500, FTSE100, ASX200）及三只美股（Microsoft, Gen Digital, Agilent Technologies），时间范围2000-2023。
- Bootstrap方法实证验证了估计分位数$\alpha{est}$在0.05-0.15区间的优越性，实际数据标准误曲线呈U型。

• 多模型VaR和ES预测比较 [page::20][page::21][page::22][page::23]:

- 28种风险预测模型对比，包括传统FHS方法（GARCH-FHS、GJR-GARCH-FHS）和QFHS方法(CAViaR-IG、CAViaR-IGJR、Realized CAViaR及其log版本)。
- 对个股，QFHS显著优于FHS，尤其是log Realized CAViaR在1天和10天预测中表现最佳。
- 对市场指数，FHS和QFHS表现相当，无显著统计优势。
- Realized类模型整体优于非Realized模型，说明利用日内波动率信息提升风险预测能力。

• 量化策略推荐与实务建议 [page::28]:

- 建议实务中针对VaR和ES的典型低风险水平(1%, 2.5%)，估计分位数宜选择0.05–0.15，既保证参数估计稳定性，也提升尾部风险预测准确性。
- 本方法适合高峰度、偏态金融时间序列，特别是个股和高频信息丰富的资产。

报告分析：Using quantile time series and historical simulation to forecast financial risk multiple steps ahead

---

1. 元数据与概览

• 标题：Using quantile time series and historical simulation to forecast financial risk multiple steps ahead

- 作者：Richard Gerlach, Antonio Naimoli, Giuseppe Storti

• 机构：

- Discipline of Business Analytics, The University of Sydney
- Department of Economics and Statistics, University of Salerno

• 研究主题：提出一种基于分位数的半参数历史模拟方法，用于多步预测金融风险测量指标Value-at-Risk (VaR)和Expected Shortfall (ES)。

- 发表时间：未明确标注，推测为近年研究。

• 核心论点与创新：

- 该研究提出了一种新的量化风险预测工具，称为Quantile Filtered Historical Simulation (QFHS)。
- 该方法基于分位数回归框架，利用分位数损失函数替代传统历史模拟中的拟似然函数，对返回数据进行标准化后，通过重采样来生成多步预测的风险分布。
- 该方法赋予VaR和ES多步预测的能力，可应用范围广，包括有条件VaR和ES之间不随时间变化关系的任何数据或模型。
- 与传统历史模拟（HS）和滤波历史模拟（FHS）方法相比，QFHS方法表现优越，特别是在高峰度和带偏态的金融数据上。
- 通过模拟和实证研究，强调了估计分位数水平（$\alpha{\mathrm{est}}$）选择的重要性，最好选择高于目标风险水平$\alpha0$范围[0.05, 0.15]。

---

2. 逐节深度解读

2.1 报告引言与背景

• VaR与ES定义及重要性：

- VaR提供给定置信水平的损失量化界限，尽管广泛应用，但缺乏一致性（不满足次可加性等性质）。
- ES作为VaR的补充，被认为是更具数学一致性和实践意义的风险度量。

• 历史模拟法局限与FHS改进：

- 标准HS方法无法有效应对数据中常见的波动聚类问题。
- FHS方法先用GARCH模型滤波数据，再用HS方法预测标准化残差的分位数，弥补了HS的缺陷。

• 职位模型CAViaR及其扩展：

- CAViaR通过分位数回归直接建模VaR动态，提供更灵活的风险预测。
- Manganelli and Engle（2004）提出了基于CAViaR的ES估计方案，但仅限于单步预测。

• 本研究创新点：

- 扩展FHS采用分位数回归滤波代替传统方差模型。
- 允许分位数估计$\alpha{\mathrm{est}}$与目标风险水平$\alpha0$不一致，从而增强灵活性。
- 利用重采样技术支持多步预测VaR和ES，满足监管（Basel协议）对10日风险预测的要求。
- 结合实时波动测量（Realized measures）进一步提升模型精准度。

2.2 方法论——QFHS方法详细介绍

• QFHS第1步建立动态分位数函数（例如CAViaR模型）估计$\alpha$水平的VaR序列。

- 利用分位数损失函数估计VaR，得到标准化残差系列$\hat{\epsilon}{\alpha,t} = rt / -\hat{Q}{\alpha,t}$。

• 关键步骤为利用重采样方法模拟未来残差路径，进而计算未来多步VaR和ES。

- 理论上，将样本中$\hat{\epsilon}{\alpha,t}$按bootstrap采样形成多条路径，再乘以未来估计的VaR，生成多步复合收益的模拟，最终通过样本分位数和尾部均值计算VaR和ES。

对比FHS：

• FHS滤波约束残差为零均值、单位方差，QFHS代以分位数标准化，残差的$\alpha{\mathrm{est}}$水平固定为-1，回归残差的分位数更贴合尾风险特性。

- 从理论上讲，FHS为最大似然估计下的特例，QFHS灵活采用多种分位数损失函数，可以适应更多实际需求。

2.3 模拟实验与估计效率分析

• 设计多种数据生成过程(DGP)，包括正态、学生t分布及偏斜学生t，涵盖不同峰度和偏态。

- 通过500次500样本大小的蒙特卡洛模拟，对比QFHS与GARCH-FHS在1步和10步预测精度。

• 主要发现：

- 对于正态分布，FHS表现略优，偏态和高峰度数据，QFHS明显优势，尤其当估计分位数$\alpha{\mathrm{est}}$在[0.05, 0.15]时表现最佳，优于直接使用目标分位数$\alpha0$。
- 多步预测同样验证上述结论，QFHS的优势在偏态和厚尾条件下更加明显。

• 理论分析基于CAViaR参数估计的渐近性质，计算不同$\alpha{\mathrm{est}}$对应的参数相对标准误，发现极端低分位点估计效率显著下降，而中间稍高的分位数更优。

- 实证模拟结果和理论指标均一致指向选择稍高于目标VaR的估计分位数更合适，以兼顾预测的稳定性与准确性。

2.4 实证研究

2.4.1 Bootstrap分析估计分位数$\alpha{\mathrm{est}}$的选择

• 以美国标普500、英国富时100、澳大利亚ASX200等股指及MSFT等三只个股为样本。

- 利用Bootstrap方法对CAViaR模型参数进行重采样估计，计算不同$\alpha{\mathrm{est}}$下的标准误。

• 结果显示所有资产在$\alpha{\mathrm{est}}$靠近0或0.25（上界）时估计标准误显著增大，中间区间（约[0.05,0.15]）标准误较低，符合此前模拟结论。

2.4.2 多模型1天和10天VaR及ES实证预测评测

• 包含28种竞争模型，涵盖标准GARCH-FHS、GJR-GARCH-FHS、Realized GARCH、Realized EGARCH及QFHS分别带有不同$\alpha{\mathrm{est}}$的CAViaR-IG、CAViaR-IGJR、Realized CAViaR等。

- 采用多种损失函数指标（单变量分位数损失、联合VaR和ES损失），以及模型置信集合（MCS）分析预测表现。

• 结果：

- 对于个股数据，QFHS方法在统计显著上优于FHS，特别是$h=1$和$h=10$的VaR与ES预测，且$\alpha{\mathrm{est}} \in [0.05, 0.15]$的模型表现最佳。
- 其中，基于实时波动测量的log Realized CAViaR (log Re-C)表现最佳，优于其他模型，尤其是$h=10$长周期预测。
- 对于市场指数系列，QFHS与FHS模型预测表现无显著差异，甚至在某些情形下FHS方法略优。
- 实时波动相关模型在个股预测中优势明显，在大盘指数中反而边际效应较弱，反映市场级别数据的结构差异。

2.5 结论

• 提出创新QFHS方法，有别于传统的滤波历史模拟，采用分位数回归和分位数损失函数，允许估计分位数与目标风险水平不匹配，增强了风险分布的模拟能力。

- QFHS在高峰度、偏态数据及多步风险预测中优于FHS，尤其适合个股等尾部特征显著的资产。

• 理论与实证一致表明选择$\alpha{\mathrm{est}}$稍大于目标风险水平（0.05-0.15）可显著提升预测性能。

- 建议实务中可采用该范围分位数估计，结合实时波动测量提升VaR和ES多步预测精度。

---

3. 图表深度解读

3.1 图1和图2（页码9）

• 描述：两个箱线图组展示500次模拟中，不同模型在VaR和ES预测中的误差分布。图1针对正态误差，图2针对偏态学生t误差。

- 解读：
- 图1显示，对于正态分布，GARCH-FHS (GHS)通常有最小误差且分布较窄。
- QFHS不同$\alpha{\mathrm{est}}$值下的性能波动显著，低$\alpha{\mathrm{est}}$往往表现较差。
- 图2（偏态厚尾）中，QFHS性能提升明显，误差中位数和离散度普遍低于GHS，尤其是中间$\alpha{\mathrm{est}}$值。

• 联系文本：

- 支持报告指出，在高峰度且偏态风险环境中，QFHS方法相比传统FHS有优势。
- 中间优选的$\alpha{\mathrm{est}}$区间对模型性能影响显著。

3.2 表1和表2（页码10）

• 描述：两表列示基于均方根误差（RMSE）的平均排名，分别对应1步和10步预测。

- 解读：
- JFHS（即QFHS的竞争对手），多为排名末尾。
- QFHS在$\alpha{\mathrm{est}} \in [0.05,0.15]$区间内表现最好，排名靠前。
- 10步预测中QFHS整体优势更明显。

• 联系文本：

- 定量支持方法论部分关于$\alpha{\mathrm{est}}$选择对预测性能敏感的结论。

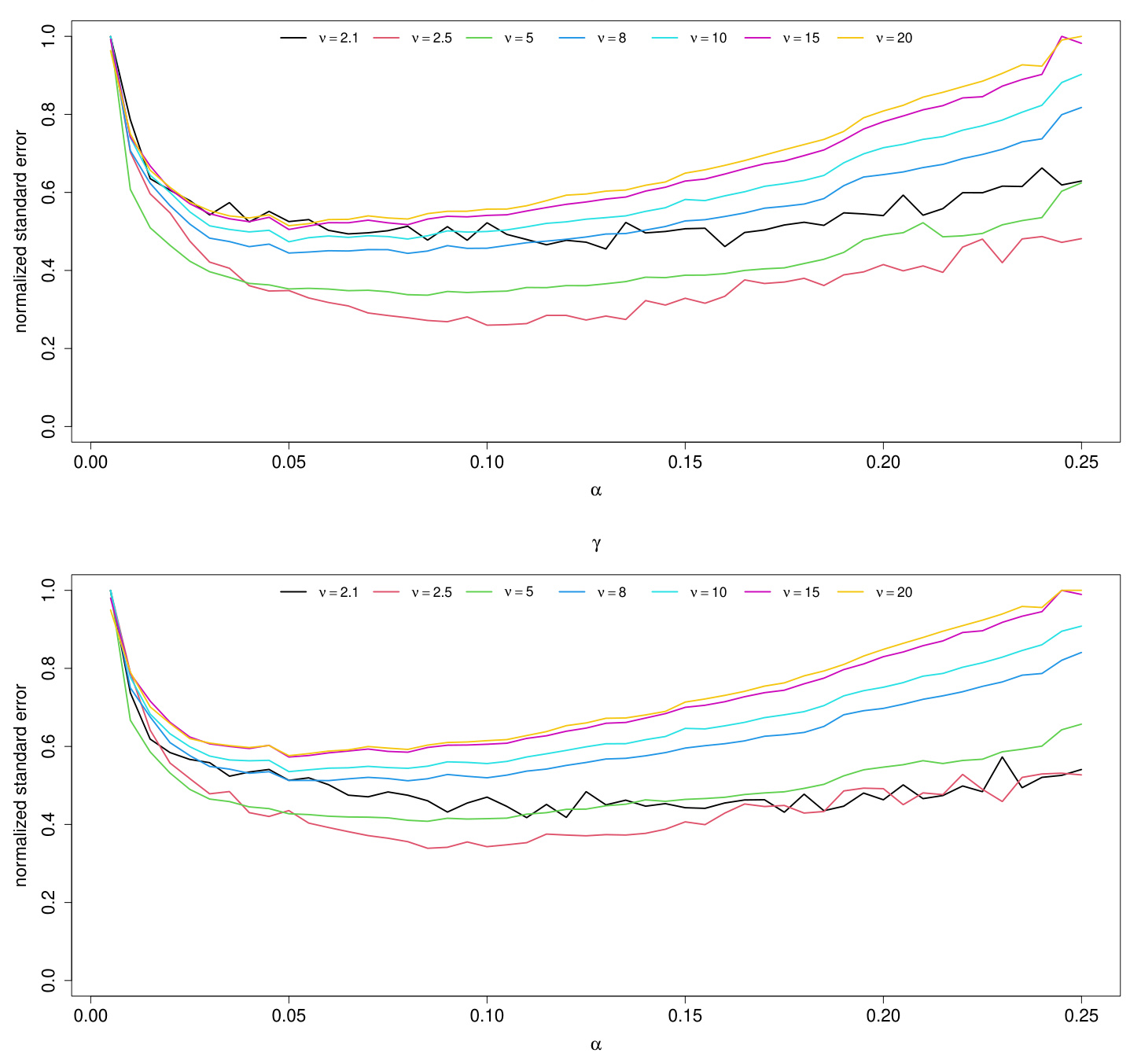
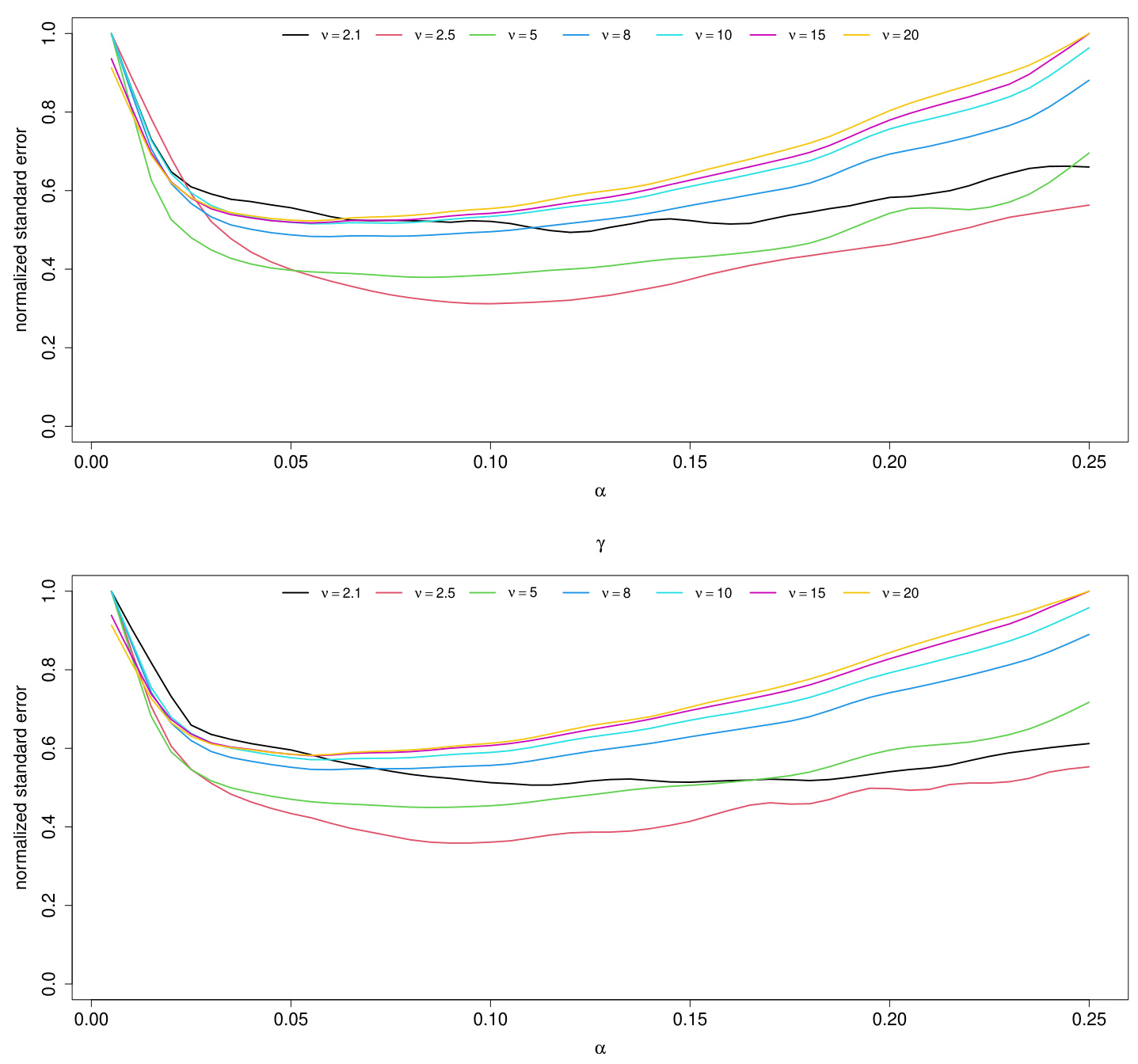
3.3 图3（页码13）

• 描述：展示不同分位数估计水平$\alpha$下，CAViaR模型系数的标准误归一化曲线，不同颜色代表不同自由度(峰度)参数$\nu$。

- 解读：
- 误差最小点大致位于$\alpha$约0.1左右。
- 尾部（极低$\alpha$）的估计误差显著较大，说明极端分位数估计效率低。
- 随着自由度增加，曲线变得平缓，峰度降低模型估计稳定。

• 联系文本：

- 该图为理论推导和模拟实验基础，解释为何中间偏高的$\alpha{\mathrm{est}}$更合理。

3.4 图4（页码15）

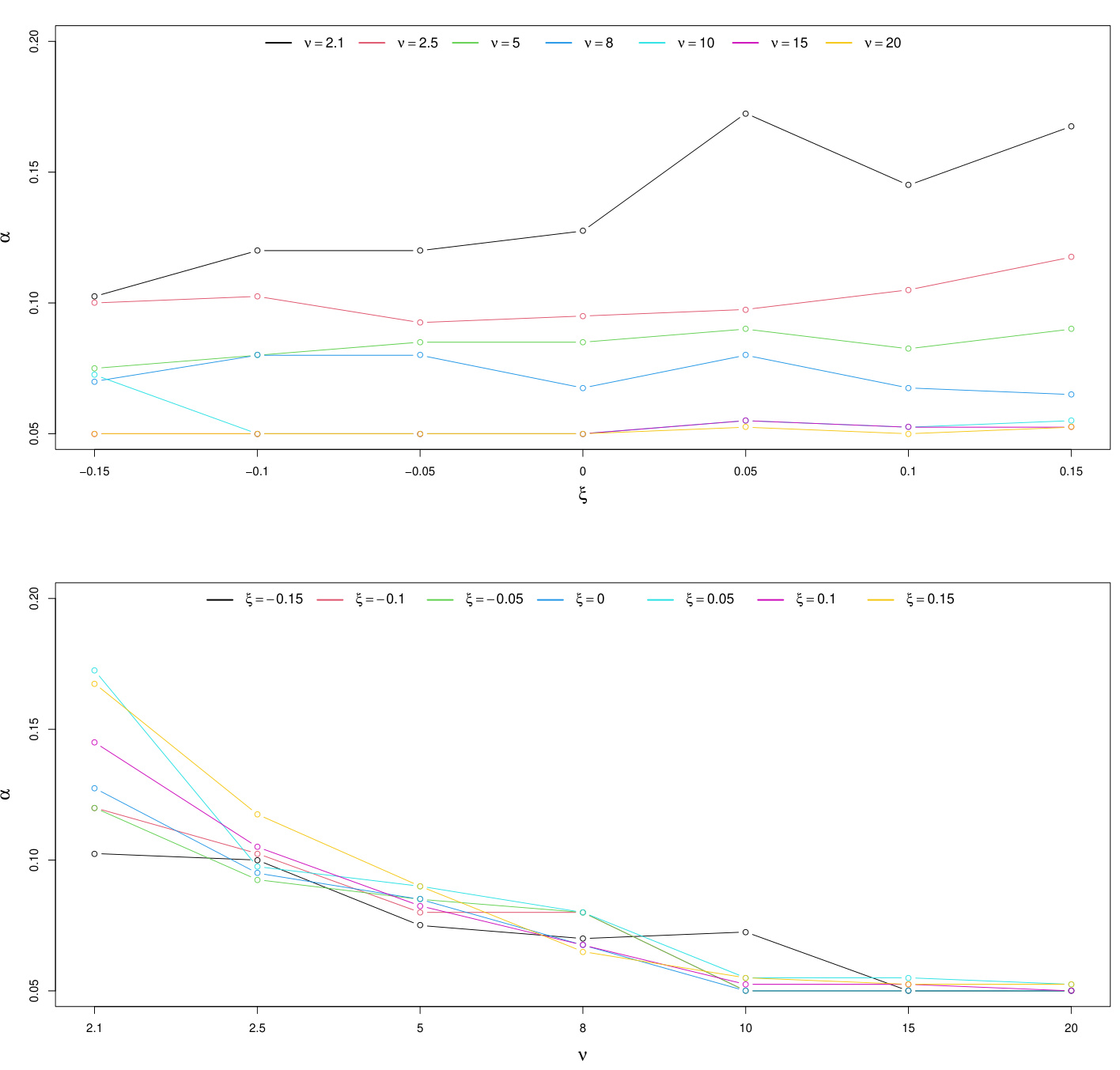
• 描述：二维线图展示最佳$\alpha$估计点随自由度$\nu$和偏态系数$\xi$变化趋势。

- 解读：
- 随峰度降低（$\nu$减少），最佳$\alpha$表现为增大趋势（推荐使用更高分位数估计）。
- 偏态影响更显著于重尾分布，偏负偏态时最佳$\alpha$适当增加。

• 联系文本：

- 进一步支持模型灵活选取$\alpha{\mathrm{est}}$的统计学合理性。

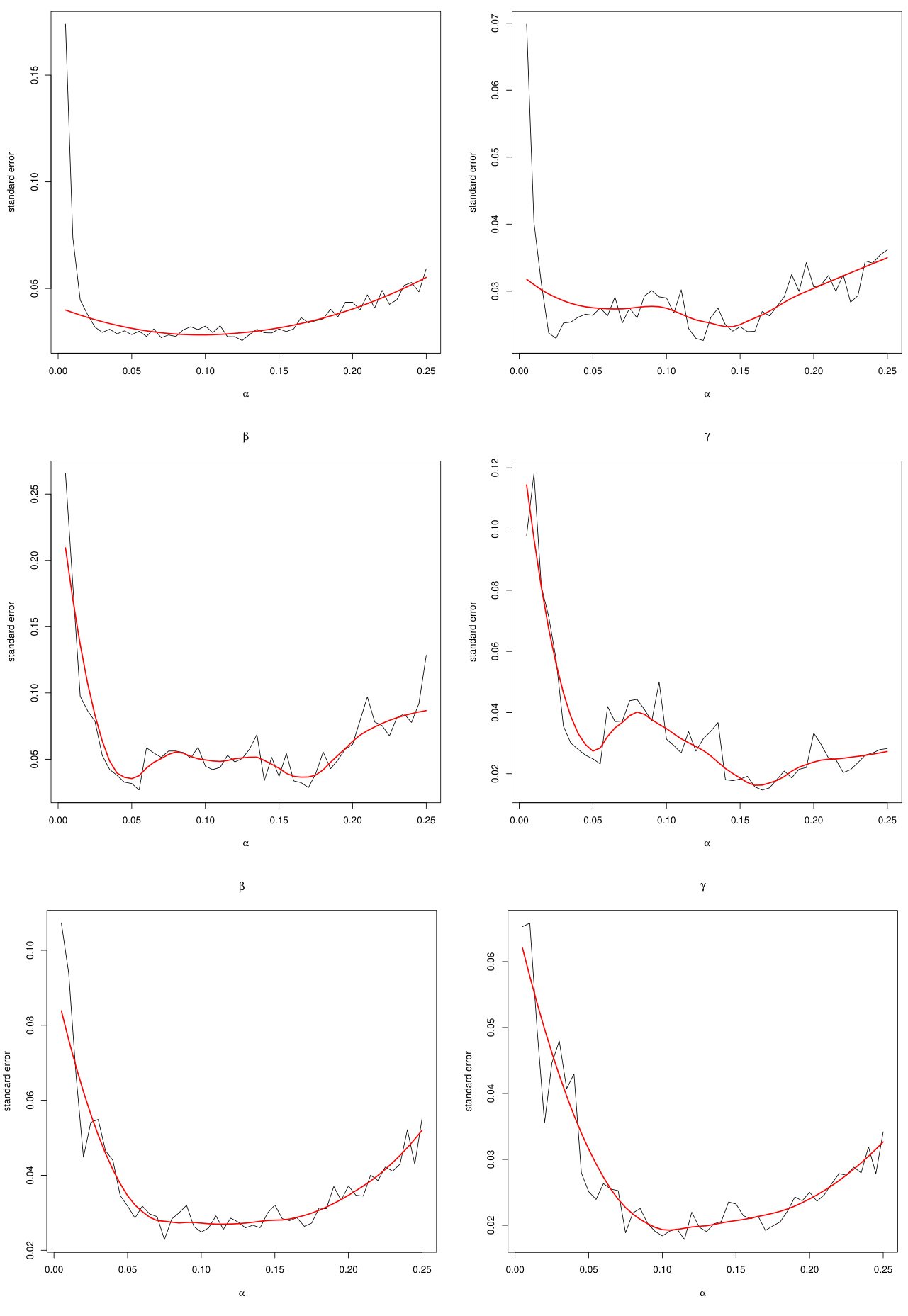
3.5 图5与图6（页码18-19）

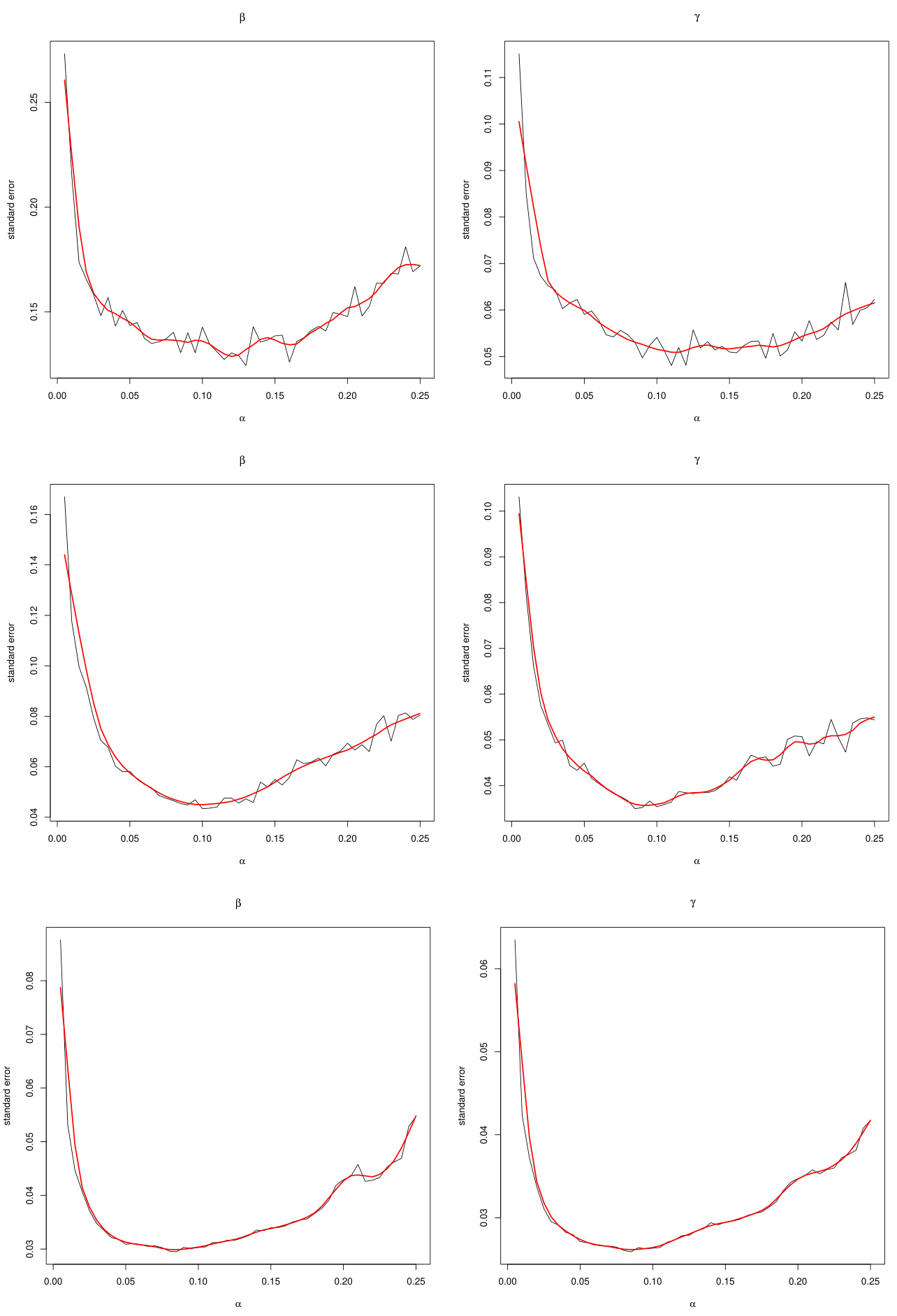
• 描述：实证数据下Bootstrap计算得到不同$\alpha{\mathrm{est}}$对参数估计标准误的影响图表，分别针对不同资产。

- 解读：
- 各资产均显示估计误差在$\alpha$区间低端和高端抬升，中间区间标准误最低。
- 拟合平滑曲线展示趋势明确，支持理论和模拟发现。

• 联系文本：

- 实时和实证验证了模拟建议，增强方法推广的可信度。

---

4. 估值分析

本报告主要聚焦于风险度量预测模型的提出与比较，未体现传统意义上的公司估值分析。报告中模型估计及方法的“估值”集中于

• 利用分位数模型估计风险度量参数；

- 通过不同方法和参数选取预测未来VaR与ES的损失或准确度；

• 不同模型间的模拟与实证性能比较。

因此不存在DCF或市盈率等估值模型，仅涉及风险预测模型估计参数的标准误及预测误差的度量与对比。

---

5. 风险因素评估

• 报告强调了传统历史模拟在面对真实金融市场波动特征（如波动聚类、偏态、厚尾）时的局限性，及其导致的VaR和ES预测偏差风险。

- QFHS通过引入分位数回归和更灵活参数选择，有效缓解数据中偏态和峰度风险，提升尾部风险测度的准确率。

• 但依然存在风险：

- 如果假设VaR和ES之间条件关系随时间发生变化，方法性能可能受限；
- 重采样方法依赖历史残差独立性假设，可能忽略极端变化的突发性与动态性；
- 模型结构基于CAViaR假设模型正确且数据大样本量情况下性能优越，小样本或模型错配时稳健性未知。

• 报告未对这些风险设置专门缓解措施，但方法本身的灵活性和实证结果提供一定程度上的风险控制和调整建议。

---

6. 批判性视角与细微差别

• 潜在偏见：

- 报告多强调QFHS优越，可能倾向性较强，尤其在个股样本，市场广泛使用FHS的背景下，揭示的缺陷或局限或被弱化。

• 稳健性担忧：

- 对于超极端风险的多步预测，重采样基于历史数据的局限性可能对尾风险预测的极端置信区间造成影响，报告中未深入讨论。

• 参数选择复杂性：

- 虽建议$\alpha{\mathrm{est}}$高于$\alpha0$，但实际操作中该区间的具体选取、模型稳定性需进一步实践验证。

• 市场类型差异：

- 实证结果显示市场指数VS个股预测效果差异，QFHS未必普适，市场与资产特征可能影响模型选择。

• 模型复杂度和计算成本：

- QFHS涉及大量重采样和参数估计，实际应用中计算复杂度较高，报告未详细讨论资源要求。

• 报告结构：

- 该文虽有丰富模拟和实证验证，但缺少对模型误差构成的更深入理论解释，未来可进一步拓展。

---

7. 结论性综合

该研究针对金融风险管理领域的VaR和ES测算，提出了一种创新量化方法——Quantile Filtered Historical Simulation (QFHS)。该方法将历史模拟中的传统方差滤波机制更换为以分位数回归为基础的滤波，使得尾部风险预测显著更加灵活和准确。尤其是在含有厚尾和偏态的金融数据情境中，多步风险预测能力良好，超越了传统滤波历史模拟（FHS）。

核心的技术贡献包括：

• 分位数回归为滤波步骤，让标准化残差具备以分位数为约束的稳定性质，适合尾部风险模拟。

- 允许估计分位数水平$\alpha{\mathrm{est}}$与目标风险水平$\alpha0$不同，实证与模拟均表明选择较高$\alpha{\mathrm{est}}$（0.05至0.15）可增强风险预测的精度和稳定性。

• 提出基于重采样的多步风险预测框架，符合监管机构针对未来10日风险评估的实际需求。

- 将实时波动测量纳入建模框架，强化对市场实时信息的利用，提高预测表现。

多项模拟与实证实证中，QFHS方法特别在个股风险数据集上效果优异，log Realized CAViaR模型表现尤为突出。相较而言，FHS方法仍具实用价值，尤其在市场指数层面表现相当，显示方法间优劣与资产特征密切相关。

最后，报告对模型估计量的标准误分析以及参数选择提出了具体建议，对金融风险管理实务与未来学术研究均有重要指导价值。

---

综上，QFHS方法代表了金融尾部风险测算的前沿进展，兼具理论剖析与实证检验，尤其适合高峰度、偏态及多步风险预测情景，是风险管理领域可供实务采用的先进工具。[page::0,1,2,3,4,5,6,7,8,9,10,12,13,15,16,17,18,19,20,21,22,23,28,31,32]

---

附：关键图表展示

图1：模拟中高斯误差VaR和ES预测误差分布（页码9）

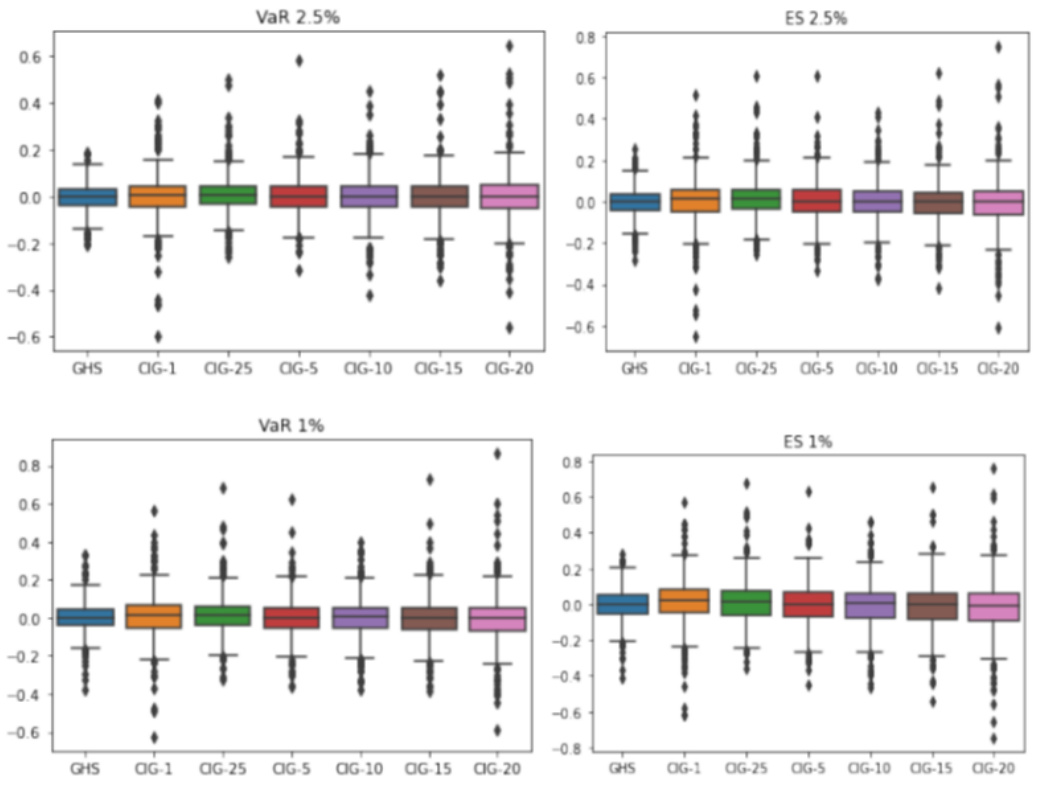
图2：模拟中偏态学生t误差VaR和ES预测误差分布（页码9）

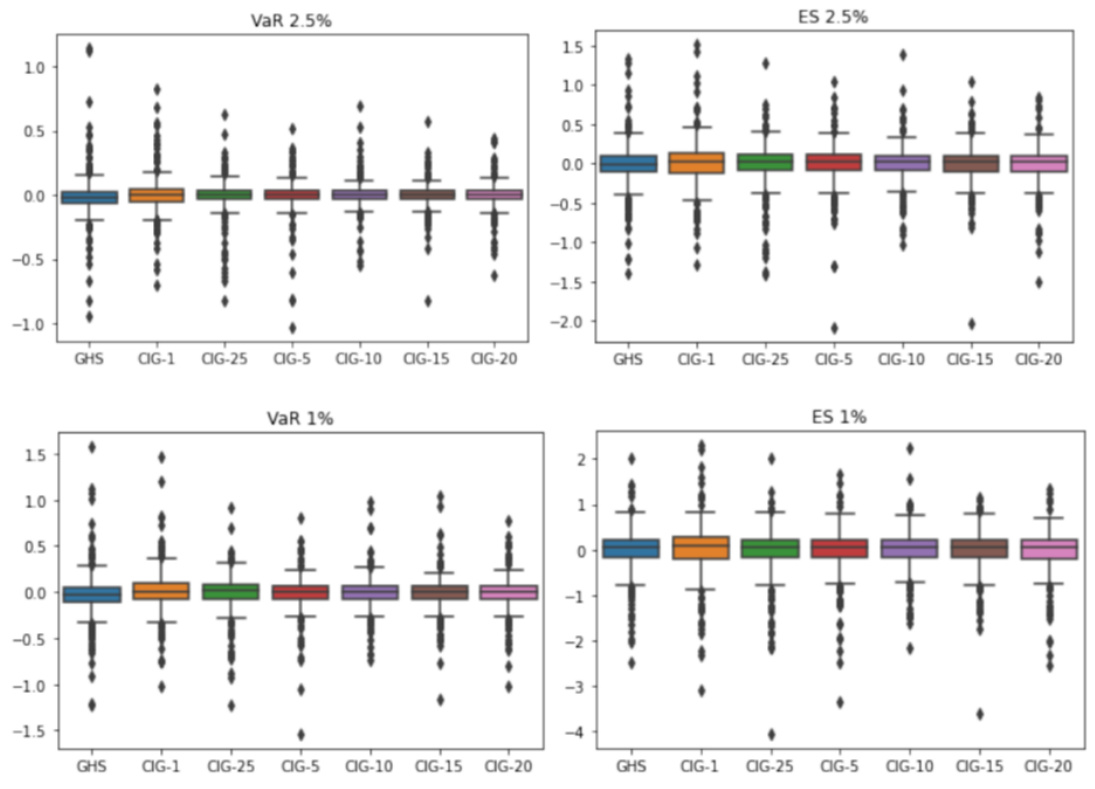
图3：归一化参数估计标准误与$\alpha$的关系（页码13）

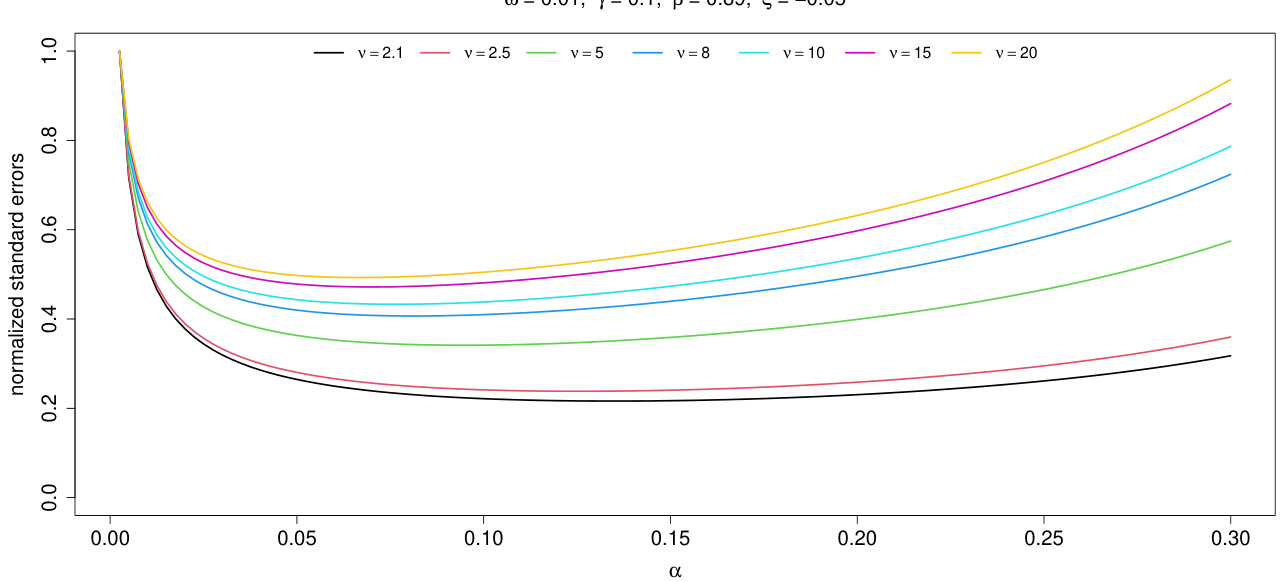
图4：最佳$\alpha$值随峰度和偏态变化（页码15）

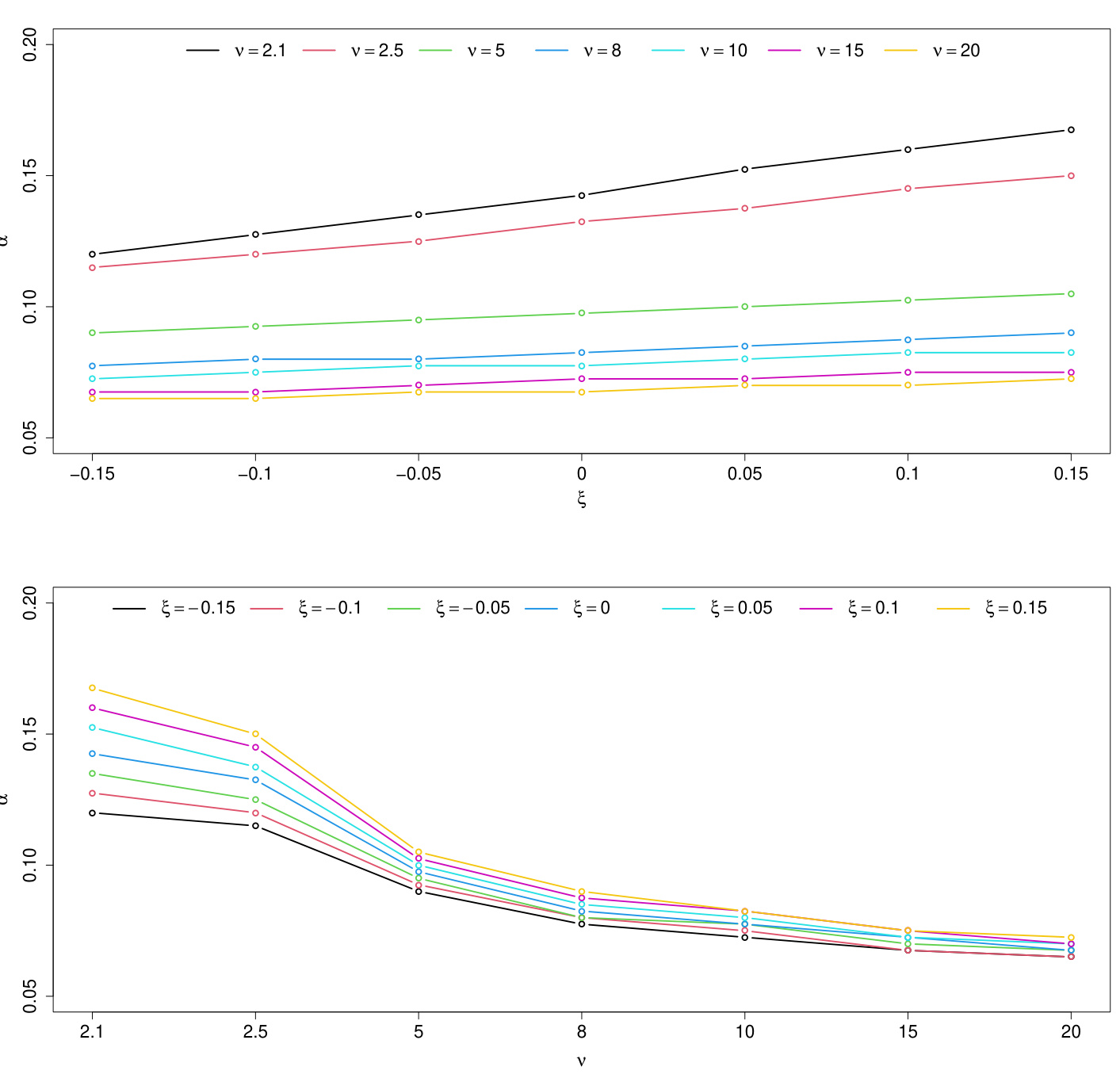
图5：实证数据Bootstrap标准误估计示例（页码18）

图6：实证数据Bootstrap标准误估计示例（不同个股）（页码19）

图A.1：附录蒙特卡洛标准误图（页码32）

图A.2：附录蒙特卡洛标准误LOESS平滑（页码33）

图A.3：附录蒙特卡洛原始与平滑标准误对比（页码34）

图A.4：附录最佳$\alpha$值随峰度与偏态变化（页码36）

报告