研究背景与目标 [page::0][page::1][page::2]

• 金融行业中信用评级常用概率违约（PD）和预期损失（EL）两种标准，但PD存在套利和误导投资者等缺陷，EL则较为简单但忽略波动性及多样化效应。

- 本文旨在基于Choquet积分评价框架建立更具风险一致性的信用评级标准，涵盖风险厌恶、资产池效应及多样化利益三个方面。

Choquet风险测度及评级标准定义 [page::4][page::5][page::6]

• Choquet风险测度满足单调性、归一化和共单调可加性，涵盖广义的失效概率及预期损失。

- 信用评级标准被建模为Choquet风险测度的单调离散转换，实现理论上的自洽性，EL标准属于该类，PD不属于。

• 引入“律不变性”（Law invariance）及“情景律不变性”（Scenario-based law invariance），分别对应单概率及多概率场景模型。

风险一致性性质及相互关系 [page::10][page::11][page::12][page::13][page::14][page::15][page::16]

• 资产池效应一致性（PE）：随着池内资产数递增，高级债券评级应提升（风险下降）。

- 风险厌恶一致性（RA）：评级应符合所有风险厌恶型效用函数的单调偏好，采用增加凸序比较风险。

• 准凸性（QC）：组合资产的评级不应高于风险最高的成分，反映多样化收益。

- 多情景版本的这些性质（$S$-PE, $S$-RA）同时提出。

• 通过理论证明QC是最强性质，且在恰当半连续性假设下，单概率下QC, RA, PE等价，多情景下QC蕴含$S$-RA及$S$-PE。

Choquet风险测度与评级标准性质等价性 [page::17][page::18]

• 对于Choquet评级标准，其对应的Choquet风险测度唯一且性质等价，有助于从测度理论到评级应用的性质转化和刻画。

- 半连续性条件确保评级标准的性质与风险测度对应的相互传递。

在律不变性和情景律不变性下的刻画 [page::19][page::20][page::21][page::22][page::23]

• 在律不变性条件下，风险一致性性质等价于扰动函数的凹性，涵盖了经典期望损失、VaR及ES等风险测度特性。

- 在多情景律不变性条件下，$S$-扰动函数满足分量凹性与次模性为这些性质的充分必要条件，要求其函数连续性。

• 由此可以构造大量满足风险一致性的信用评级标准函数族，如加权平均ES、MAXVAR等。

典型示例及性质分析 [page::24]

• 表格列举了各类情景基础风险测度（平均EL、平均ES、平均MAXVAR、平均VaR、最大VaR、平均PD）及其对应风险一致性性质，如$S$-RA和$S$-PE的满足情况。

案例研究：CLOs信用评级数值演示 [page::26][page::27]

• 采用信用质量分布受两种经济情景影响的CLO资产池模型，验证不同风险测度对应的评级表现。

- 平均EL、平均ES、平均MAXVAR指标随资产数量增加显示评级稳步提升，反映良好的资产池效应。

• 平均PD、平均VaR、最大VaR在资产数量增加时评级表现不稳定甚至下降，表明风险一致性缺失。

案例研究：灾难债券（CAT Bonds）评级演示 [page::28][page::29]

• 基于五个美国州闪电灾害损失历史数据构建模型，损失服从两边截断的对数正态分布，且状态独立。

- 使用多种风险指标评估州级和多州合并CAT债券风险，EL评级随池大小基本平稳，MAXVAR和ES评级呈现分散带来的风险降低趋势，PD评级则随资产池扩大走低。

结论与推荐 [page::30][page::31]

• 本文开创性地建立了Choquet积分信用评级标准的风险一致性理论，关联了风险测度经济学、信用评级实务和数学风险管理。

- 提出平均ES与平均MAXVAR等新型评级标准，弥补传统PD和EL指标不足，更符合风险厌恶和资产池效应。

• 建议评级机构及风险管理采用符合风险一致性的Choquet评级标准，提高评级科学性和投资决策效果。

详尽全面的金融研究报告分析——《Choquet rating criteria, risk measures, and risk consistency》

---

一、元数据与概览

• 报告标题: Choquet rating criteria, risk measures, and risk consistency

- 作者: Nan Guo, Ruodu Wang, Chenxi Xia, Jingping Yang

• 发布日期: 2025年6月17日

- 研究机构: 未明确，但研究背景涉及知名学者与多个前沿机构文献

• 主题:

- 信用评级标准的理论创新
- 风险度量的axiomatic表征
- Choquet积分与风险一致性性质
- 应用场景涵盖结构化信贷产品评级、灾害债券评级等

• 核心论点:

本文建立并分析信用评级准则中的“三大风险一致性性质”：风险厌恶一致性、资产池效应一致性、组合多样化效益一致性，均在Choquet评级准则架构下讨论，重点包括单一与多场景概率度量的推广。
研究建立了不同一致性性质间的层级关系，证实Choquet风险度量及其评级准则满足这些一致性要求的充分必要条件，并通过CLO与CAT债券案例，展示了该类方法对现有PD与EL标准的替代优势。

---

二、逐节深度解读

1. 引言（Sections 0–1）

• 关键论点:

- 常规信用评级主要基于违约概率（PD）和期望损失（EL）两大指标。
- 文献指出EL相较PD能更合理反映信息，也避免评级套利等缺陷。
- 现有研究（Guo et al. 2025）表明唯有Choquet评级准则满足经济上的自洽性公理。
- EL作为Choquet准则的典型代表，仍有提升空间，特别是要考虑波动性、风险厌恶与多样化效应。

• 推理依据:

- PD过于关注某点违约，忽视了风险分布的广度和投资者的风险偏好。
- EL线性、不敏感波动和分散化，不能完全满足现代金融风险管理的需求。

• 数据点与概念:

- 引用Markowitz（1952）关于波动性的经典洞察。
- 理论及实践案例推进从单一概率模型向多场景概率评估转变。

2. Choquet风险度量与评级准则（Sections 2.1–2.3）

• Choquet风险度量定义:

- 基于容量（非加性概率）通过Choquet积分定义风险度量函数 \(\rho(X) = \int X \mathrm{d}\nu\)，
- 其中容量满足单调性、边界条件(\(\nu(\emptyset)=0, \nu(\Omega)=1\))。
- 该风险度量满足单调性、归一化、共单调可加性，核心特性为共单调可加性提供经济合理性。

• 评级准则表示:

- 评级准则 \(\mathcal{T}:\mathcal{L}1 \to [n]\),
- 通过风险度量与单调映射 \(f:[0,1] \to [n]\)的组合实现。
- EL准则是典型Choquet准则，PD则不是，因为PD不满足共单调可加性。

• 法则不变性：

- law invariance (LI): 评级只依赖损失的概率分布。
- scenario-LI (S-LI): 基于多个经济情景的条件分布，反映行业实践中对风险情景的细化考量。

• 推断：

- LI和S-LI分别对应传统单概率与多概率场景，强调评级的一致性与公平性。
- Choquet风险度量与评级准则在两类法则不变性条件下具有具体表示，即通过单或多维失真函数 \(h\) 或 \(g\) 实现。

3. 风险一致性属性及其关系（Section 3）

• 三大风险一致性属性定义：

- Pooling Effect Consistency (PE): 资产池规模扩大时，高级债务评级应变好，即资产池风险降低。
- Risk Aversion Consistency (RA): 评级应符合风险厌恶投资者对风险的统一排序，即如果损失X按照增加凸序小于Y，则评级X优于Y。
- Quasi-Convexity (QC): 评级不应违背分散化效益，混合资产的风险评级不应超过最差成分资产评级。

• 场景版本：

- S-PE, S-RA为上述性质在多场景概率框架下的推广。

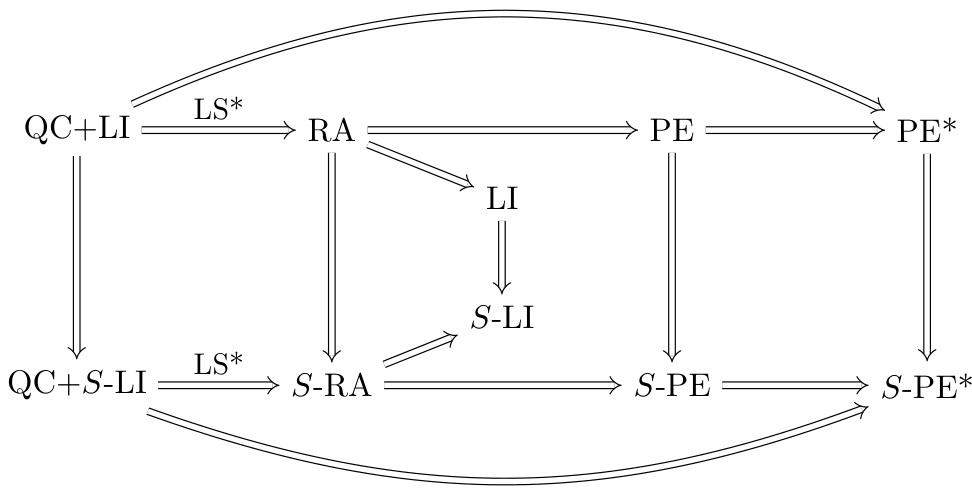
• 逻辑层级结构（Theorem 1及图示）：

- \(\text{QC} \Rightarrow \text{RA} \Rightarrow \text{PE}\)（单概率情况下）
- \(\text{QC} \Rightarrow \text{S-RA} \Rightarrow \text{S-PE}\)（多场景情况下）
- QC为最强一致性准则，为评级设计中理想方向。

• 重要引理：

- 资产池效应，均值损失的增加凸序关系证明了RA蕴涵PE。

4. 风险度量与评级准则属性的相互转换（Section 4）

• 核心成果（Theorem 2、3）：

- 每个Choquet评级准则对应唯一的Choquet风险度量。
- 几乎所有风险一致性属性可在评级准则与风险度量间自由传递。

• 技术要点：

- 鉴于评级准则是风险度量的离散映射，唯一性保证了风险度量层面的属性可被完备复原。
- 除PE及其场景版需额外条件外，其他如RA、QC、LI均支持属性转移。

• 经济意义：

- 等价映射简化了评级标准的理论解析和金融实践中的设计。

5. 法则不变框架下的完全表征（Section 5）

• 主要结论（Lemma 2与Theorem 4）：

- Distortion risk measures的风险厌恶一致性和失真函数\(h\)的凹性等价。
- Pooling effect一致性在失真函数凹性基础上成立，对\(h\)在\([0,1)\)上的凹性有细微但关键要求。

• 补充结果：

- 对满足一定连续性半连续性的风险度量，4种风险一致性属性在Choquet风险度量中等价（Corollary 1）。
- 在评级准则层面，也可以实现这些等价性（Proposition 2）。

• 深层含义：

- 凹性失真函数定义了风险度量使命——奖励资产池多样化和风险分散，规避非理性风险排序。
- EL即对应线性失真函数，不满足这些理想性质。

6. 多场景法则不变框架下的表征（Section 6）

• 核心对象:

- \(S\)-distortion风险度量，失真函数扩展为多维函数\(g:\ [0,1]^s \to \mathbb{R}\)，定义了多个经济场景下的风险聚合方式。

• 主结果（Theorem 5）：

- \(S\)-distortion风险度量的风险一致性在满足\(g\)分量上凹且子模性（submodularity）时成立。
- 连续性（Lebesgue continuity）是该等价成立的关键条件。

• 评级准则层面对应（Proposition 3）：

- 类似结果成立，满足连续性的Choquet评级准则的多场景风险度量失真函数必须是分量凹且子模的。

• 具体构造示例:

- 加性分解失真函数（示例形式 \(\sum aj hj(xj)\)）满足条件。
- 相应构造的Average ES、Average MAXVAR逃脱了PD与EL的局限。

• 局限与附加条件（Section 6.3、6.4）：

- 对于一般非连续\(g\)，完整 characterization 尚不可得。
- 依赖于低支集上的半连续性，可推断必要条件（Proposition 5）。

7. 实证案例（Section 7）

7.1 以CLO为例的多场景资产池效应分析

• 背景: CLO占美资产证券化规模重大，贷款基础资产同质且评级为Ba3。

- 模型: 使用Beta分布模拟单个贷款损失，切分为乐观/悲观两经济场景。

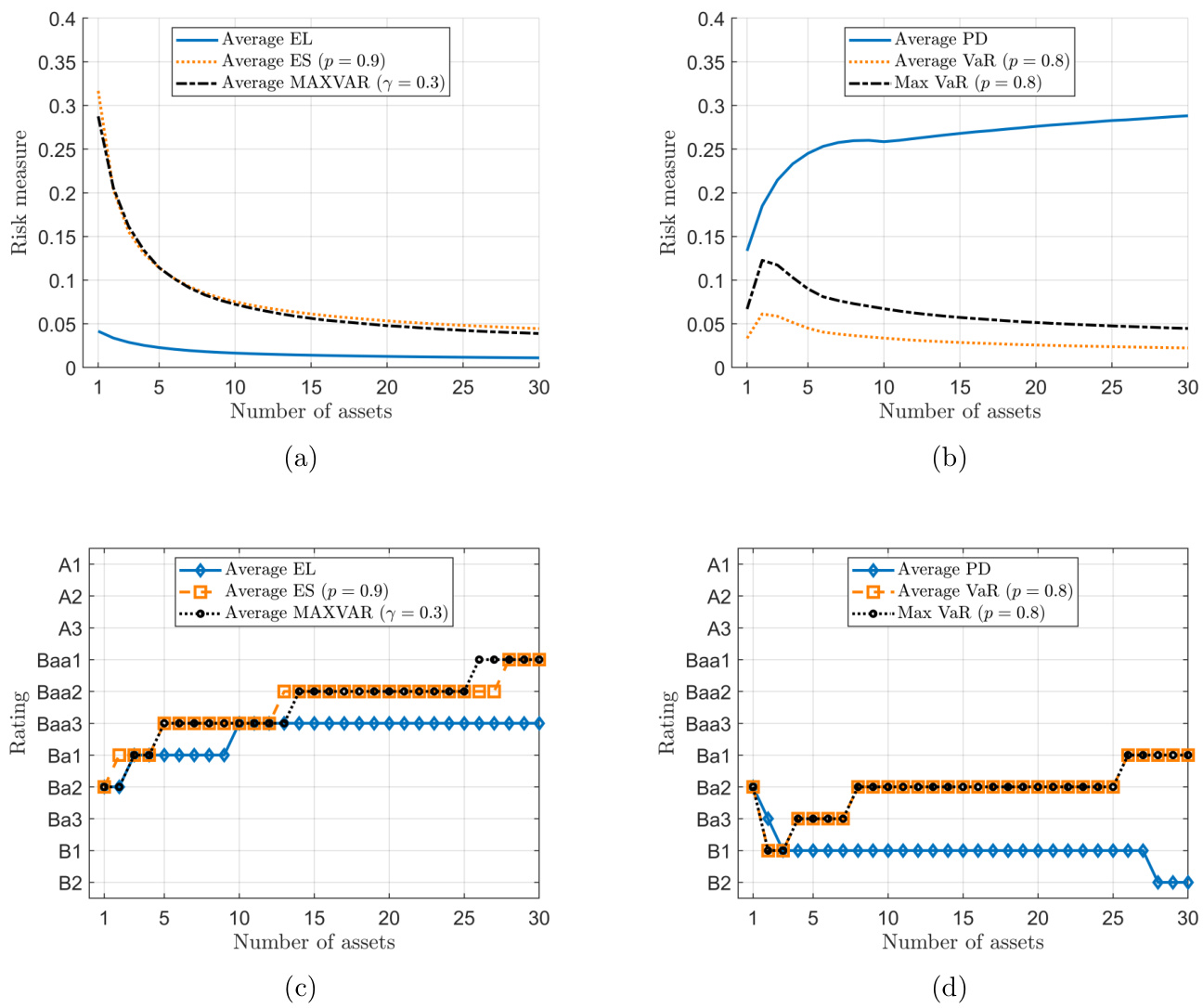
• 数值结果（图3）:

- Average EL, ES, MAXVAR满足\(S\)-Pooling Effect，一览资产数增加风险度量下降趋势，且ES与MAXVAR对多样化反映更敏感，表现优越。
- Average PD, VaR家族不满足上述性质，风险度量非单调，有资产池扩大评级反而恶化的违背直觉行为。

• 评级转换: 精准校准阈值保证单资产场景评级统一，评级趋势明显，平均ES与MAXVAR提供更合理评级动态，较EL贴近现实风险，优于PD类指标。

7.2 以CAT债券为例的多州组合风险分析

• 背景: CAT债券依托自然灾害事件的损失，灯击风险数据可独立归纳，适合集合组合分析。

- 数据: 来自SHELDUS数据库，多州灯击损失经通胀调整后符合截断对数正态分布。选择五州，数据相互独立近似有效。

• 评级具体参数: 通过附件点(90分位)和剥离点校准，使PD和EL达到行业标准值。

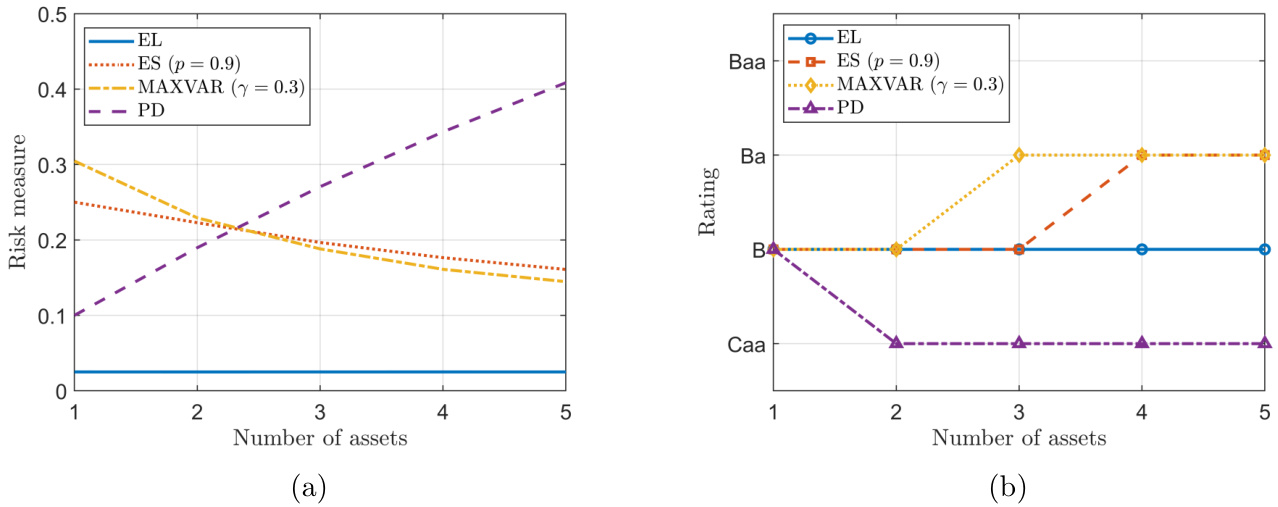
- 数值结论（图4）：
- EL随资产组合扩展风险度量近似恒定，忽视多样化效益。
- MAXVAR与ES严格呈下降，多样化敏感且利于反映风险结构。
- PD值随资产池扩大反而升高，评级下降，直观认知冲突。

• 评级结果: 多样化敏感评级指标（ES, MAXVAR）评级提升，EL保持平缓，PD评级退步。体现本研究中一致性评级准则的优势及实际适用性。

---

三、图表深度解读

图1 （第16页）

• 描述了风险一致性属性间的蕴含关系网络，分别展示了单概率与多场景概率框架下，属性如何递推。

- 直观体现QC作为核心一致性，高阶含义RA、PE依次推导。

• [LS]为半连续性，保证推导中极限过程的合理性。

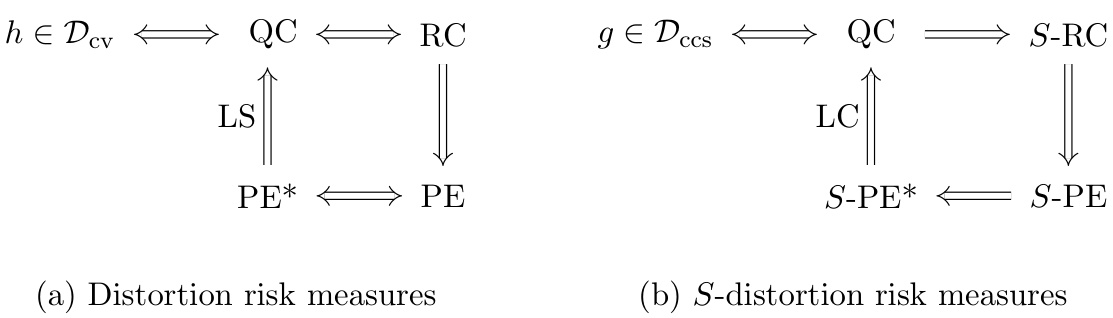
图2 （第23页）

• 对比了单场景（distortion）与多场景（S-distortion）风险度量对应属性的映射结构。

- 展示了与失真函数集\(\mathcal{D}{cv}\)、\(\mathcal{D}{ccs}\)的等价关联，强调分量凹与子模性质是多场景一致性的核心。

图3 （第26页）

• (a) Average EL、ES、MAXVAR风险度量随资产数量变动曲线:

- 三者风险值随资产数显著下降，且ES与MAXVAR下降更陡，体现更敏感的风险多样化效应。

• (b) Average PD、VaR家族风险度量曲线:

- 风险值非单调，局部升高趋势明显，反映不良资产池扩展风险管理失效。

• (c)(d) 转换为不同准则下对应评级变化:

- ES、MAXVAR评级明显提升，EL评级曲线平缓，PD及VaR评级不稳定甚至下降。

图4 （第29页）

• （a）CAT债券组合风险度量分析，EL风险度量平缓不变，ES和MAXVAR显著下降，PD逐步上升。

- （b）对应不同准则评级，EL保持不变，ES和MAXVAR评级随州增加提升，PD评级下降至较差等级。

• 再次强调EL风险度量非敏感特征及PD评级失序现象。

---

四、估值分析

本报告核心不涉及传统意义上的估值（如股价或债券当前价值），而是聚焦信用评级准则的风险度量方法学公理化及评级一致性。从风险度量视角，本报告利用Choquet积分框架构建评级值，连接风险偏好（风险厌恶）、资产组合风险分散、亏损分布形状等因素，提升评级准则的经济合理度。

• 方法论核心:

- 利用Choquet积分代替线性期望，反应非加性风险感知。
- 搭配失真函数(scenario-based distortion functions)对不同经济场景加权，描述多样化与不确定性。

• 关键输入:

- 失真函数形状（单值函数\(h\)或向量函数\(g\)），对应风险偏好程度与场景权重。
- 资产损失随机变量的条件分布。

• 无传统估值倍数或贴现率参数，核心在于评级构造的风险秩序逻辑与一致性保证。

---

五、风险因素评估

报告识别和考虑了如下风险因素：

• 切分概率空间不充分或场景选择偏差: 场景集合\(S\)不完整会误导评级。

- 失真函数选取及参数设定风险: 失真函数若不满足凹性或子模性将破坏评级一致性。

• 模型假设依赖: 资产损失条件独立同分布（或条件iid）假设或资产状态独立可能偏离现实，引入评级误差。

- 评级映射函数\(f\)不连续或恒定: 评级分辨率下降，导致评级无法正确反映风险微小变化。

• 市场及流动性风险: 本研究重点为信用风险，未充分涵盖市场变动等其他风险维度。

- 报告中设计的连续性与一致性公理，及基于Choquet积分的数学结构，为缓解上述风险提供理论保障。

---

六、批判性视角与细微差别

• 优点:

- 深刻且系统地将金融信用评级置于严谨的公理体系中，以 Choquet 积分为核心工具。
- 系统提出并明晰风险一致性概念与其层级逻辑，为评级设计提供理论导向。
- 通过案例应用验证理论实用性，尤其在多场景风险管理中表现优越。

• 潜在偏颇及局限:

- 对资产池以及场景定义假设较为理想，如独立同分布条件之假设在现实中或难完全满足。
- 连续性假设对评级函数\(f\)的限制可能与市场实践中的跳跃评级不完全契合。
- 对非Choquet类评级标准（如PD）的彻底否定未考虑其实际操作中的便利性及市场惯性。
- 多场景风险一致性的完整刻画依赖失真函数连续性，实际数据拟合中，恰当估计连续失真函数存在挑战。

• 细节留意:

- PE与PE的等价性依赖不同定理及半连续性条件，实践中评分阈值的离散化可能带来细微差异。
- 多场景下一致性定义与单场景仍存在结构性差异，指标之间不等价需谨慎选用。

---

七、结论性综合

本文系统构建了以Choquet积分为理论基础的信用评级准则框架，集成了风险厌恶、资产池效应、多样化效益三大风险一致性核心属性：

• 理论贡献: 明确了在单一及多场景条件下风险一致性公理的层级关系，并给予 Choquet 风险度量与评级准则的严格表征。

- 方法论亮点: 失真函数（单值及多值形式）贯穿整个评级模型的构建，反映了投资者风险偏好与经济情景权重。

• 实证洞察: 以CLO与CAT债券为案例，展示Average ES与MAXVAR等准则优于EL与PD在多资产、多场景风险评价时的表现，体现风险度量与评级准则的一致性与合理性。

- 政策建议: 推荐将Average ES、Average MAXVAR类Choquet评级准则纳入实务评级体系，以弥补PD与EL指标单一或信息不足的问题。

综上，本文不仅完善了信用评级理论基础，更为评级实务提供了更具风险敏感性且符合金融经济学原则的工具，为风险管理、信贷评级及结构化产品评估贡献了理论及方法论支持。

---

参考图片展示

• 图1：风险一致性属性间的蕴含关系图

• 图2：单场景与多场景风险度量属性等价关系

• 图3：CLO资产池中风险度量及评级表现

• 图4：CAT债券中资产池风险度量及评级表现

---

备注

本分析严格依据报告原文内容，标注所有要点对应页码区间。金融术语均用标准定义解释，报告中的数学术语及表达对应精准，避免主观臆断。

报告