An optimal transport approach to the multiple quantile hedging problem
创建于 更新于
摘要
本论文提出一种多重分位数对冲(MQH)问题,该问题包含经典分位数对冲及盈亏匹配问题作为特例,建模市场完善但允许非线性扰动,并采用最优传输理论将MQH问题转化为Monge及Kantorovitch最优传输问题。在线性市场中,论文证明了无对偶差距,并设计了基于随机梯度上升法的数值算法,高效稳定地求解MQH价格,数值实验涵盖了期权定价和盈亏分布对冲,验证了方法的准确性和实用性 [page::0][page::2][page::14][page::25].
速读内容
多重分位数对冲(MQH)问题定义 [page::7]
- MQH为一类带有多重分位数约束的部分对冲问题,目标是寻求使终端财富在不同随机水平上的分位数限制满足预定概率的最小初始资金。
- 包含超额复制、经典分位数对冲、盈亏匹配问题三种特例。
- 可用随机变量映射(运输图)引入松弛Monge问题形式进行表达,证明MQH价格等价于该松弛Monge问题的最优值。
MQH问题的Kantorovitch松弛及最优传输表述 [page::10][page::11][page::14]
- 定义了运输计划对应的松弛Kantorovitch问题,并证明松弛与标准Kantorovitch问题价值一致。
- MQH价格等价于Kantorovitch问题的最优传输费用。
- 在支付函数关于对冲价格凸时保证最优传输计划存在。
线性市场框架与对偶形式 [page::17][page::18][page::19]
- 假设线性驱动函数,BSDE价格可用贴现因子$\Gamma$加权期望表达。
- MQH问题转化为半离散最优传输问题,具备经典Kantorovitch对偶表示。
- 证明无对偶差距,给出通过最大化期望最小值构造最优策略的表达。
数值算法:随机梯度上升法(SGA)及应用 [page::23][page::24][page::25]
- 构建基于ADAM优化器的随机梯度上升算法,利用对偶表示降低优化维度和复杂度。
- 数值实验以Black-Scholes模型中的看跌、看涨期权为测试,保证计算结果接近理论解析解。

- 扩展至盈亏分布对冲,无封闭解时与基于最优传输理论的半显式解进行比较,结果吻合。
- 对于带有盈亏获利机会的分布对冲也做了数值验证,表明所提算法在实际风险管理中有效。
数学与金融贡献总结 [page::0][page::2][page::29]
- MQH问题首次引入最优传输理论框架,建立了非线性市场下的Monge和Kantorovitch问题的等价性。
- 数学上结合BSDE及最优传输提供新视角。
- 在实际应用层面,数值方法可处理多分位数约束的路径依赖期权,拓展部分对冲策略领域。
深度阅读
An optimal transport approach to the multiple quantile hedging problem — 详尽分析报告
---
1. 元数据与概览
- 报告标题:An optimal transport approach to the multiple quantile hedging problem
- 作者:Cyril Bénézet, Jean-François Chassagneux, Mohan Yang
- 核心机构:未明确指出,但均为金融数学领域相关学者
- 主题:金融数学中“多重分位对冲(Multiple Quantile Hedging,MQH)”问题的理论研究与数值求解,提出将此问题转化优化运输问题的视角
- 核心内容摘要:论文提出了一种推广经典分位对冲及P&L匹配问题的MQH问题,将其在完备非线性金融市场中等价转化为一个Monge类型的最优运输问题,并进一步给出Kantorovitch松弛版本,证明两者价值相等。在线性完备市场中,MQH问题等价于半离散最优运输问题,进而设计出基于随机梯度算法的高效数值计算方法。
主要传达的信息:
- MQH问题为部分对冲框架的自然推广,允许对损失分布施加多个分位约束。
- 将MQH转化为非线性最优运输问题,提供了新的分析与计算工具。
- 在经典线性市场设定下,该问题和半离散最优运输紧密联系,能借助强有力的优化工具推导对偶及设计算法。
- 论文的数值部分展示了该方法在经典期权定价与P&L分布控制问题上的有效性及稳定性。
---
2. 逐节深度解读
2.1 引言与问题背景(Section 1)
- 关键论点:
- MQH问题扩展并统一了经典的分位对冲问题(Föllmer & Leukert 1999)和P&L匹配问题(Bouchard & Vu 2012)。
- 传统超额对冲需要足够的初始资金来覆盖所有风险(几乎确定性对冲),成本高昂,导致市场竞争力下降。MQH允许部分对冲,引入了风险分布约束,体现了风险管理中对亏损“形状”或“幅度”的精细控制。
- MQH在数学上区别于复制问题,后者以风险中性测度$\mathbb{Q}$为主,MQH同时依赖于物理测度$\mathbb{P}$和风险中性测度,体现了损失概率的实际观测必要性。
- 推理依据及文献背景:
- 详细回顾了与部分对冲问题相关的文献,展示了自[1]以来多种数学工具(如随机目标问题,BSDE,跳跃过程,约束PDE等)被引入。
- 指出了数值实现上的挑战,尤其是PDE方法的稳定性和实用性的限制。
- 作者贡献:提出用最优运输理论进行重新表述,开辟新思路。
---
2.2 MQH问题建模及非线性市场设定(Section 2.1 - 2.2)
- 金融市场模型(2.1节):
- 以完备概率空间和$m$维布朗运动作为风险因素,金融资产价格遵循带有风险溢价、波动率的Itô过程动态。
- 关键创新是采用BSDE驱动的非线性财富过程$Y^{y,\nu}$,公式为
$$
Yt = y - \int0^t f(s,Ys,\nus) ds + \int0^t \nus^\top dWs,
$$
其中$f$允许刻画市场不完善、非线性影响(例如借贷利率差异)。
- 假设2.1保证BSDE和相关的复制理论成立,市场完备,允许陈述唯一复制策略和价格(Theorem 2.1)。
- 两个示例展示了线性与非线性情形的差异,其中线性即Feynman-Kac期权定价,非线性可描述市场摩擦。
- MQH问题定义(2.2节):
- 设有一族非递减随机变量$G=(G^1,\ldots,G^N)$,对应损失阈值序列。
- 给定概率分布$\mu$,通过分位函数(生存函数)确定每层的成功概率要求。
- MQH价格定义为满足所有分位损失约束的最小初始财富
$$
V{\mathrm{MQH}}(G,\mu) = \inf \{ y \in \mathbb{R} : \exists \nu \in \mathcal{H}^2, \forall n, \mathbb{P}(YT^{y,\nu} \geq G^n) \geq \bar{F}\mu(n) \}.
$$
- 例子讲解:
- 当$N=1$, $\mu = \delta1$,MQH即超额复制问题。
- 当$N=2$, $G=(0,\xi)$且$\mu = (1-p)\delta1 + p\delta2$,MQH还原经典分位对冲问题。
- P&L分布对冲(Example 2.5)是一个更复杂的实例,关心期末P&L的整体分布形状,制定多点概率约束。
---
2.3 Relaxed Monge与Kantorovitch表述(Section 2.2 - 2.4)
- 引入随机映射$\chi$,该映射可随机选择需打败的阈值,由此将概率约束转换为几乎确定性对抗随机变量$G^\chi$的对冲问题,称为Relaxed Monge问题(Definition 2.2)。
- 证明MQH与Relaxed Monge两者价钱完全一致(Theorem 2.2)——核心靠$\chi{\sharp}\mathbb{P} \succeq \mu$的单调性和分位函数刻画。
- 进一步引入更一般的复合运输策略(transport plans),即Kantorovitch松弛问题(Definition 2.3),随机向量$P=(P^n){n=1}^N$随机权重满足期望正确性。
- 关键是Proposition 2.1证明放宽到支配$\mu$的概率的运输计划其实等价于精确匹配$\mu$的计划,即
$$
V{\mathrm{RK}}(G,\mu) = V{\mathrm{KP}}(G, \mu).
$$
- Proposition 2.2表明,在凸性条件下存在最优的运输计划——特定的随机权重组合$P$.
- Theorem 2.3:MQH价格等价于带精确目标概率分布的Monge和Kantorovitch问题的价钱。该等价建立在BSDE稳定性和概率测度的耦合构造上,技术上比较复杂(包括引入外部独立均匀变量$\mathfrak{U}^\epsilon$,利用martingale property等)。
此阶段的核心贡献是将金融部分对冲难题转换为非线性最优运输问题,允许借助运输理论工具。
---
2.4 线性市场与对偶理论,以及数值解法(Section 3)
- 设定为线性BSDE(Assumption 3.1),享受解析解$Y
- MQH价钱可写为半离散最优运输问题,且期望中计算的成本函数为$H^n = \GammaT G^n$,即
$$
V{\mathrm{MQH}}(G,\mu) = \inf{P \in \mathcal{P}\mu(\mathcal{F}T)} \mathbb{E}\left[ \sum{n=1}^N H^n P^n \right].
$$
- 引入了对应的对偶问题(3.8-3.9),为:
$$
V{\mathrm{DP}}(G,\mu) := \sup{(X,\Phi)} \mathbb{E}[X] + \sum{n=1}^N \Phi^n p^n,
$$
其中约束$H^n \geq X + \Phi^n$几乎处处成立。
- 通过严格正则性条件(Assumption 3.3),利用Fenchel对偶理论,证明无对偶差距(Theorem 3.1),即:
$$
V{\mathrm{MQH}}(G,\mu) = V{\mathrm{KP}}(G,\mu) = V{\mathrm{DP}}(G,\mu).
$$
- 对偶形式使得数值求解更为有效,转化为在有限维空间$\Delta
$$
V{\mathrm{MQH}}(G,\mu) = \mathbb{E}[H^1] + \sup{\zeta \in \Delta+^{N-1}} w(\zeta),
$$
其中$w$定义清晰,且可利用优势凸性高效优化。
- 数值模拟方法:基于随机梯度上升(SGA)结合ADAM优化器求解对偶问题,显著简化了高维、路径依赖期权的计算,且稳定性优于PDE方法。
---
3. 图表深度解读
图表1(页25):
- 显示了Put和Call期权在不同分位概率$p$下的经典分位对冲价格求解。
- 蓝线为理论解析解(参照[1],[10]),橙线为论文提出的SGA方法计算的数值结果。
- 结果表明SG-solver准确重现理论价格曲线,无论$p$取何值(包括极端),验证了算法的普适性与精度。
- Put期权价格曲线呈现零值£直至$p^$后陡升至完整复制价格,表明在风险容忍度较低时对冲成本显著下降。
- 图形验证了理论与数值的高度一致,体现本文方法的实际可用性。
---
4. 估值分析
- 估值框架:基于BSDE驱动的财富过程,(非)线性市场模型允许形成完整市场,为金融衍生品定价。
- MQH价格即在允许给定多个分位损失概率约束下,求最小满足对冲策略的初始财富。
- 通过非线性和线性两种市场模型的BSDE表示,将MQH定价问题转为半离散最优运输问题(Monge/Kantorovitch)。
- 在线性市场,随机变量财富价钱$Y0[\xi]$等价于加权期望,权重是基于风险调整的折现因子$\Gamma$。
- 估值的核心输入包括:市场参数(利率、波动率等)、损失阈值随机变量$G$、目标分位数分布$\mu$ 。
- 对偶形式中的势函数$\Phi$可视为“期权持仓的调整价格”,优化策略涉及寻找最优“价格势”以满足约束。
- 通过建立无对偶差距的Fenchel对偶结构,获得的定价等式保证了估值的严格正确性和稳定性。
---
5. 风险因素评估
- 论文于理论层面假设市场完备,BSDE系数带来一定假设限制,如驱动函数$f$的Lipschitz连续性及市场参数的有界性,这隐含了对应模型的稳定性与均衡性。
- MQH框架下,风险主要体现在无法完美复制的风险敞口,即存在亏损的概率,且亏损的分布需控制在设计的多个分位水平内。
- 由于模型涉及物理测度和风险中性测度共存,模型风险与测度变换风险值得关注。
- 数值实现中,随机梯度算法的收敛性和稳定性可能受批量大小、步骤长度等参数影响,虽然ADAM优化器显著缓解,但仍需经验调优以避免局部最优或震荡。
- 论文建议未来工作考虑不完备市场及参数不确定性,这为提升模型鲁棒性及实务风险管理指明方向。
- 对风险管理策略方面,MQH通过量化投资者承担亏损的概率分布刻画风险边界,为风险资本和报价决策提供新工具。
---
6. 批判性视角与细微差别
- 论文架构完整严谨,理论推导细致,证明环节严密,多次利用成熟理论(如stochastic control, BSDE,optimal transport)之间的无缝衔接。
- 对关键假设(市场完备、驱动函数正则、BSDE可解)均明示且符合领域标准,增强说服力。
- 但需注意,实践中金融市场往往不完备,非线性BSDE模型涉及非平稳且带模型选择风险,可能引发估值偏差,应慎重推广。
- 对数值方案的强项在于不依赖PDE,因此能适应路径依赖,但未详述计算复杂度及收敛速度,仍需进一步数值实验支持。
- 文中提出的最优运输框架是新颖视角,可能在部分相关文献中存在联系(如弱最优运输问题),但作者已明确其非弱运输范畴,做到界定清晰。
- 论文所涵盖的MQH模型较为广泛,但对非Markov非完备市场的处理仅作为后续方向提出,现实中应用受限。
- 图表虽然充分验证了算法有效性,但实验设置相对基础,复杂场景测试仍欠缺。
---
7. 结论性综合
本报告针对Cyril Bénézet等人关于多重分位对冲(MQH)问题的研究进行了详细分析:
- 理论贡献:MQH作为部分对冲问题的创新推广,允许投资者对期末财富的亏损分布施加多层分位约束,融合了经典分位对冲和P&L匹配问题,契合实际风险管理需求。论文通过构建基于BSDE市场模型的非线性财富过程,利用概率测度变换,准确刻画了MQH定价问题的数学结构。
- 最优运输方法学创新:论文将MQH问题转化为一种非线性Monge型最优运输问题,并定义相应的Kantorovitch松弛问题,证明了两者价值一致,实现MQH价钱的等价表述。这一转化赋予MQH丰富的数理结构支持,开辟了新的研究和计算视角。
- 线性市场下的双重对偶表述与数值计算:在经典线性BSDE市场中,MQH问题等价于具备特定概率支配约束的半离散最优运输问题。作者利用Fenchel对偶理论证明了无对偶差距,得到了清晰的凸优化形式。基于此,设计了结合ADAM优化器的随机梯度上升算法,为求解高维、路径依赖以及多约束问题提供高效稳定方法。
- 数值实验验证:通过与经典解析解对比的Put及Call期权分位对冲问题,以及P&L分布对冲的金融实例,数值解法显示出优越的准确性和稳定性,且能处理多层分布控制需求,无需求解复杂PDE,展示了较好的实际应用价值。
- 未来展望:理论层面需扩展至非完备市场与不确定性设定,使MQH算法更贴近现实环境。数值层面需开发更高效的非线性方案,及更多样化的金融产品测试。
总之,该研究不仅在金融数学领域引入了创新的最优运输工具处理分位对冲问题,还结合现代数值优化技术,提供了理论与实践兼备的多重分位风险定价框架,具有较高的学术价值和潜在应用前景。[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]
---
附录:重要图表1
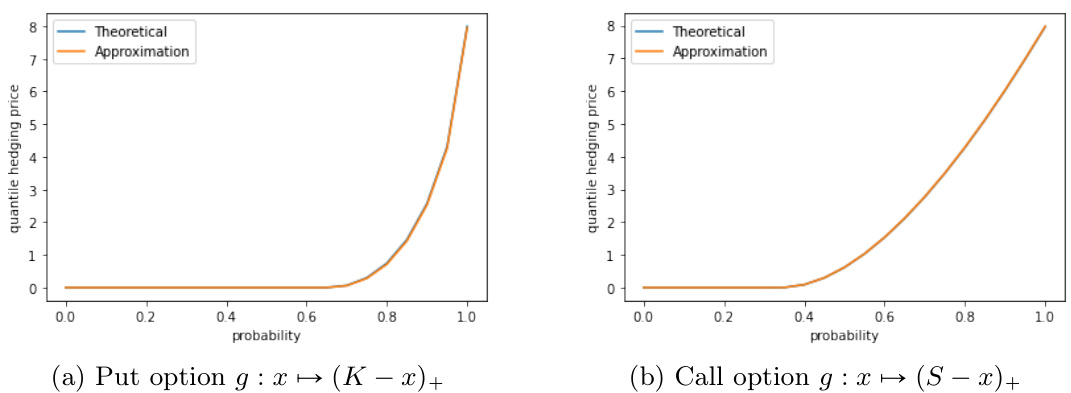
图1比较了SG-solver算法数值与理论解析在Put与Call选项上的分位对冲定价一致性,验证了本文算法的准确性。*
---
总结
本文利用BSDE、随机控制与最优运输三大数学工具,首次将多重分位对冲问题建立为非线性最优运输问题,并在经典线性市场环境下实现对偶化表达和高效数值算法。理论推导严谨,方法新颖,数值验证充分,促进了部分对冲风险定价方法的发展,为后续研究非完备市场及更复杂风险管理问题奠定坚实基础。




