Lifted Heston模型简介及参数化设置 [page::0][page::1][page::2]

• Lifted Heston模型是对经典Heston模型的多维Markovian推广，描述波动率为多个均值回复过程的加权和，捕捉粗波动特征。

- 特殊参数化利用Hurst参数H与维度N控制模型粗糙度，实现对粗Heston模型的收敛。

• 模型包含状态过程向量U，尺度参数ω与均值回复速度λ及波动率ν等，形成(5+2N)参数体系。

整合方差隐式模拟框架及线性投影方法 [page::3][page::4][page::5][page::6]

• 仿真基于积分方差X与随机积分Z的隐式关系，利用Dubins-Schwarz定理将X映射为布朗运动首次通过时间，分布服从逆高斯。

- 通过在L2空间对Z在X上的条件线性投影，确定最优线性拟合系数(α,β)，使误差最小。

• 利用矩阵微分方程计算条件期望和协方差，包括状态过程积分，以及X和Z间协方差，保证拟合的精确性。

有约束线性投影算法（C-LP）设计及保证正定性 [page::10][page::11][page::12][page::13]

• 为保证模拟方差非负，引入对β参数的约束，定义可行域，确保更新的方差路径总为正。

- 约束条件化简为单个闭区间条件，通过KKT条件求解优化问题得到约束的最佳β。

• 算法步骤从模型参数和当前状态计算条件期望、协方差，调节β确保样本有效，采样逆高斯分布后更新状态及价格。

数值实验和性能验证 [page::15][page::16][page::17][page::18][page::19][page::20]

• 线性投影拟合图显示拟合良好，误差主要来源于逆高斯二阶矩与真实X的差异，参数灵敏度分析表明波动率初值和波动率波动度影响最大。

- 约束参数β有效避免产生负波动率样本，保证模拟路径有效性。

• 收敛测试显示C-LP相比Euler方法能使用更大步长且误差显著下降，性能稳定。

- 波动率衍生品定价（VIX期权）实验表明C-LP在较少时间步情况下准确还原隐含波动率，Euler方案在小步长以外表现不佳。

• 相较Abi Jaber/Attal方案，C-LP拟合更优，收敛速度更快，且能稳定处理更复杂参数集。

总结贡献与意义 [page::20]

• 该工作设计了Lifted Heston模型的高效隐式积分方差蒙特卡洛模拟算法，基于最优L2线性投影和逆高斯分布采样，显著提升计算效率。

- 约束优化保证模拟过程的稳定性和正定性，扩展了其在实际金融衍生品定价中的应用范围。

• 方法比现有方案收敛更快，能显著缩减时间步数需求，推动粗波动率模型的数值模拟与应用进程。

Lifted Heston Model: Efficient Monte Carlo Simulation with Large Time Steps — 深度分析报告

---

1. 元数据与概览

标题: Lifted Heston Model: Efficient Monte Carlo Simulation with Large Time Steps
作者: Nicola F. Zaug, Lech A. Grzelak
机构: Utrecht University（Mathematical Institute）、Rabobank（Financial Engineering）
发布日期: 未明确具体日期（最新引用文献至2025年）
主题: 金融数学中的随机波动率模型，特别是Lifted Heston模型的高效蒙特卡洛模拟方法。

该报告目的是提出一种新颖且高效的蒙特卡洛模拟算法，针对Lifted Heston模型的积分方差过程进行采样，允许在较大时间间隔下实现数值模拟，提升效率且保持较高精度。核心贡献为引入一种基于$L^{2}$最优线性投影（Linear Projection）的隐式积分方差（IVI）采样方法，并通过约束保证模拟量的合理性（称为C-LP方法）。

作者传达的主要信息为：

• 通过建立积分方差与扩散驱动量之间的最优线性关系，能够大幅提高仿真步长，避免Euler等传统方法小步长所带来的计算负担和数值不稳定。

- 利用逆高斯分布采样积分方差过程，结合C-LP保证数值的非负性和稳定性。

• 新方法在数值稳定性、精度和效率方面均优于现有IVI方法和Euler方法，特别适合于具有粗糙波动率特征（Rough Volatility）的Lifted Heston模型。

---

2. 逐节深度解读

2.1. 报告摘要与引言

引言中点明随机波动率作为金融衍生品定价的核心模型，强调Rough Volatility模型在捕捉实际波动率市场特征（如ATM隐含波动率陡峭度）中的优势。经典的Heston模型发展为Rough Heston模型，后者基于带有分数阶Beta核的CIR型均值回复过程。问题在于这种模型的非马尔可夫性质导致数值框架缺乏，进而影响模拟和校准效率。

为解决非马尔可夫性，通过将带有分数核的过程拆分为多维Markovian过程——Lifted Heston模型。[1]提出了该模型，通过有限个“状态”过程($N$个均值回复状态)来近似粗糙波动率过程。此模型虽然马尔可夫，但涉及高维和小步长Euler模拟存在计算开销和稳定性风险。

作者因此提出基于IVI方案的新的模拟方法，利用积分方差和驱动扩散过程之间的线性近似，采用逆高斯分布采样积分方差，显著扩大仿真步长，提升效率与准确性[page::0-1]。

---

2.2. Lifted Heston模型定义与参数化

模型定义为如下SDE系统：

• 资产价格过程$St$满足：

$$
\frac{dSt}{St} = r dt + \sqrt{Vt} dWt^1
$$

• 波动率的积分表示为多个均值回复状态过程的加权和：

$$
Vt = g0(t) + \sum{n=1}^{N} \omegan Ut^n
$$

• 各状态$Ut^n$如下：

$$
dUt^n = (-xn Ut^n - \lambda Vt) dt + \nu \sqrt{Vt} dWt^2
$$

其中$Wt^1$, $Wt^2$存在相关系数$\rho$，$g0$为确定性函数拟合初始概率分布曲线，$\lambda, \nu$为均值回复速度和波动率的波动率（Vol-of-Vol）。该模型在$N=1$，权重和均值回复指数特定取值时退化为经典Heston模型。

为减小参数空间复杂度，作者引入参数化方法利用额外Hurst指数$H \in (0, 0.5)$控制参数$\omegan, xn$，确保Lifted模型逐渐收敛至粗糙Heston模型[1]，达到连续过程的极限。该参数化规律为
$$
rN = 1 + 10 N^{-0.9}, \quad \omegan, xn \text{按} rN, H \text{定义}
$$
保证了本模型广泛的灵活性与理论约束性[page::1-2]。

---

2.3. 传统仿真方法与问题

报告指出，Euler-Maruyama (EM)为经典的随机微分方程系统数值解法，但其要求微小步长以确保$L^2$强收敛，且在较大步长时对波动率过程易产生负值，需附加反射或吸收修正，带来偏差[11,4,18]。
此外，Broadie-Kaya提出跳出逐步仿真思路，直接采样积分方差实现精确模拟，但计算较为昂贵[10]。后续的研究[15,5,2,3]沿用采样积分方差的原则，发展了多种轻量级模拟方法，效果显著优于原始Euler模拟。Abi Jaber 和 Attal提出基于逆高斯分布的IVI方案，样本生成速度快于高斯采样，但采用右端点积分近似导致误差依赖步长，难以适用极大步长[page::2]。

---

2.4. C-LP方法理论框架

核心创新在于，作者不用简单的积分近似，而是通过在$L^2$空间中对积分方差$X{s,t} = \ints^t Vu du$和扩散过程积分$Z{s,t} = \ints^t \sqrt{Vu} dWu^2$做最佳线性投影，得到最优线性拟合模型：

$$
\hat{X}{s,t} = \alpha + \beta \hat{Z}{s,t}
$$

其中$\alpha, \beta$通过条件期望和协方差计算获得，确保最小均方误差。此线性关系使得$X$的分布可表示为布朗运动首达时间，符合逆高斯分布[14]，实现了积分方差的高效采样。

利用Dubins-Schwarz定理将$\hat{Z}{s,t}$标准化为布朗运动时间变换，提供理论支持。作者进一步详尽推导了状态过程积分$X{s,t}^n$的期望和协方差，使得多维状态过程一致且可解。该过程涉及线性系统矩阵$A=-\lambda \mathbf{1}N \omega - \mathrm{diag}(x)$的指数矩阵及其谱分解，计算要求部分数值积分，但仅需单次求解即可复用，确保效率。

这套方法实质上是给出了积分方差与状态扩散之间的最佳线性近似解，避免了传统方法中直接积分带来的误差，支持较大的离散时间步长而无显著损失[page::3-9]。

---

2.5. 算法实现及约束

基于上述理论，得到具体算法步骤（称为C-LP算法）：

• 对于每时间步段$[ti, t{i+1}]$，根据当前状态$\boldsymbol{U}{ti}$计算$\alphai = \mathbb{E}{ti}[X{ti,t{i+1}}]$和$\betai = \frac{1}{\alphai} \mathbb{E}{ti}[X{ti,t{i+1}} Z{ti,t{i+1}}]$，构造最佳线性预测

- 样本$\hat{X}{ti,t{i+1}}$从逆高斯分布采样，$\hat{Z}{ti,t{i+1}} = (\hat{X}{ti,t{i+1}} - \alphai)/\betai$计算

• 对多维状态变量$\hat{X}{ti,t{i+1}}^n$进行一致线性采样，更新状态

- 计算新期间波动率$\hat{V}{t{i+1}}$和价格$S{t{i+1}}$

为保证模拟波动率非负，算法加入约束机制限制$\betai$在可行域$(0, \beta^Li]$内，且满足约束函数$Ci(0, \betai) \ge 0$（保证下期波动率正），通过求解优化问题调整$\betai$，保证数值稳健性和物理合理性。证明显示该可行域非空且$\betai$最优解可显式表达，算法因此有效且健壮[page::10-13]。

---

2.6. 算法性质及弱收敛性

论文对该方法的数值性质进行了理论证明：

• 弱一致性: 随步长$h \to 0$，该模拟法的均值和方差极限符合Lifted Heston原模型的设定动态

- 对积分方差、波动率过程的一阶、二阶矩收敛，且模拟误差随着步长减小消失

• 即使存在约束修正，算法依然保持弱一致性，约束项在步长趋零时的影响渐小[page::14-15]。

此性质保证该算法作为数值方案的稳定性和合理性。

---

3. 图表深度解读

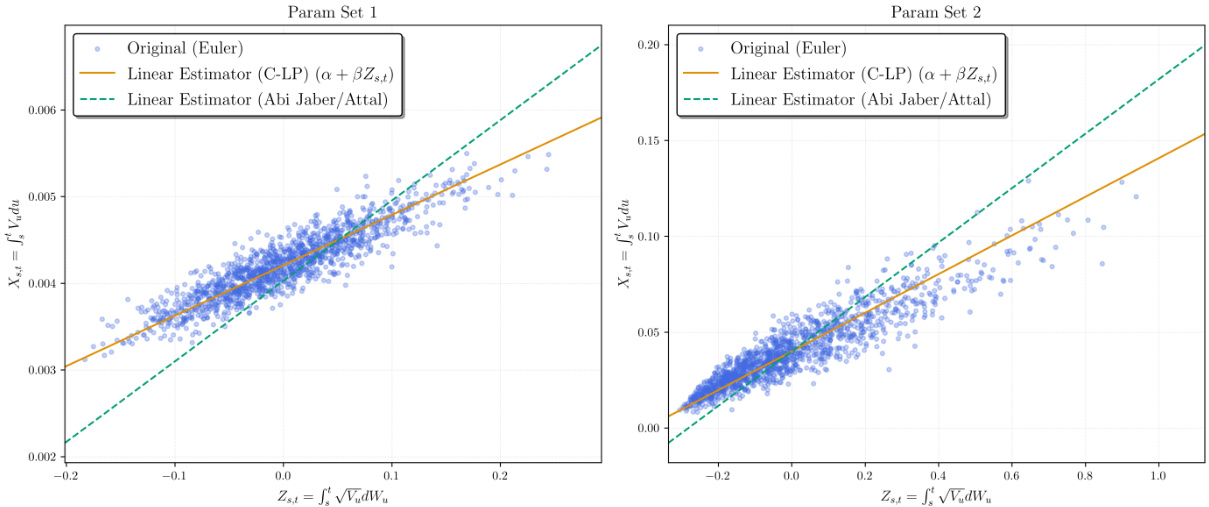
3.1. 图1（线性关系拟合示意）[page::16]

• 描述: 图1展示两组参数下，积分方差$X{s,t}$与扩散过程积分$Z{s,t}$的样本散点及通过C-LP法计算的线性拟合$\alpha + \beta Z{s,t}$，左图为$H>0.5$情况（负斜率），右图为$H<0.5$情况（正斜率）。

- 解读: 散点围绕直线分布，表明强线性关系。拟合误差等于$e{s,t} = X{s,t} - (\alpha + \beta Z{s,t})$，其方差反映近似的好坏。误差与逆高斯分布的二阶矩关系密切，参数敏感度表明$v0, \theta, \nu$的变化强化误差，$\rho$对误差无影响。

• 意义: 该图支持线性投影近似为积分方差与驱动过程间的有效模型，为C-LP方法打下基础。

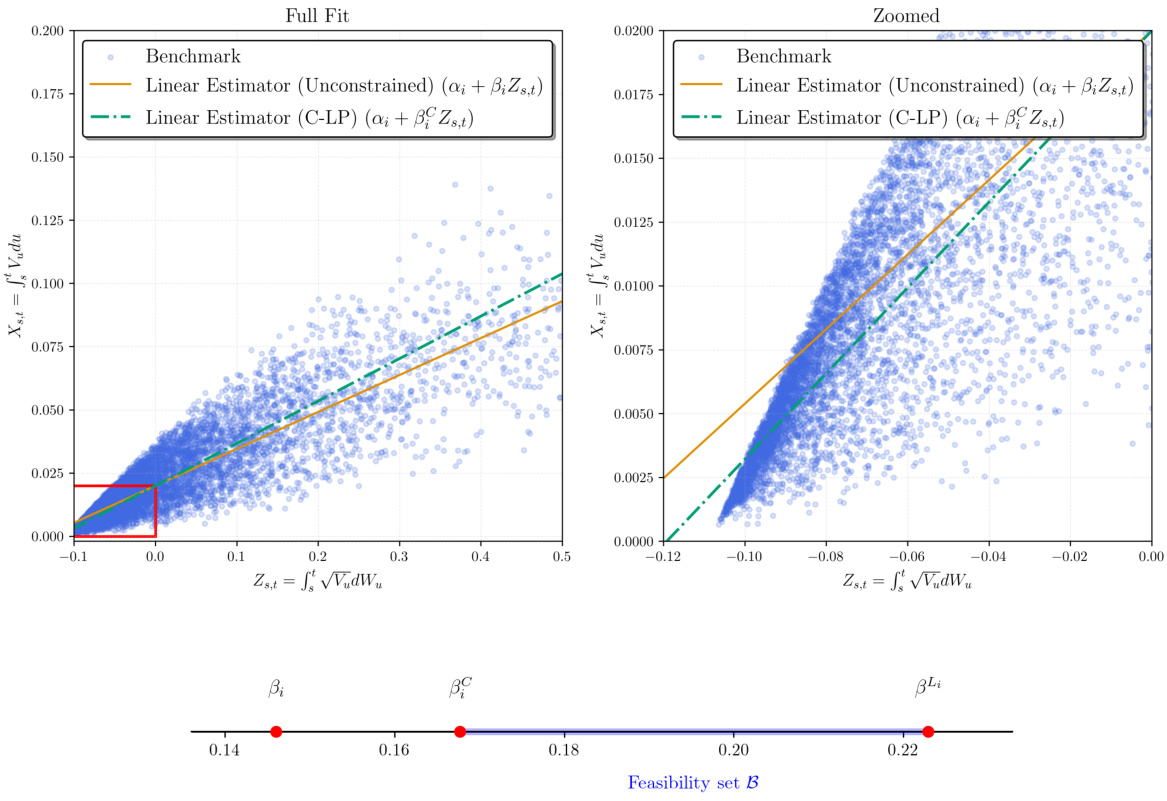
3.2. 图2（约束对比）[page::17]

• 描述: 图中出现未经约束的$\betai$导致模拟样本波动率出现负值，显示为样本点在水平轴负区。约束后的$\betai^C$置于可行区间内，保证波动率非负。

- 解读: 该图验证了约束机制对保证模型合理性的必要性，尤其参数极端时。

• 意义: 证实理论中对约束的重要性，这是实际落地中的关键步骤。

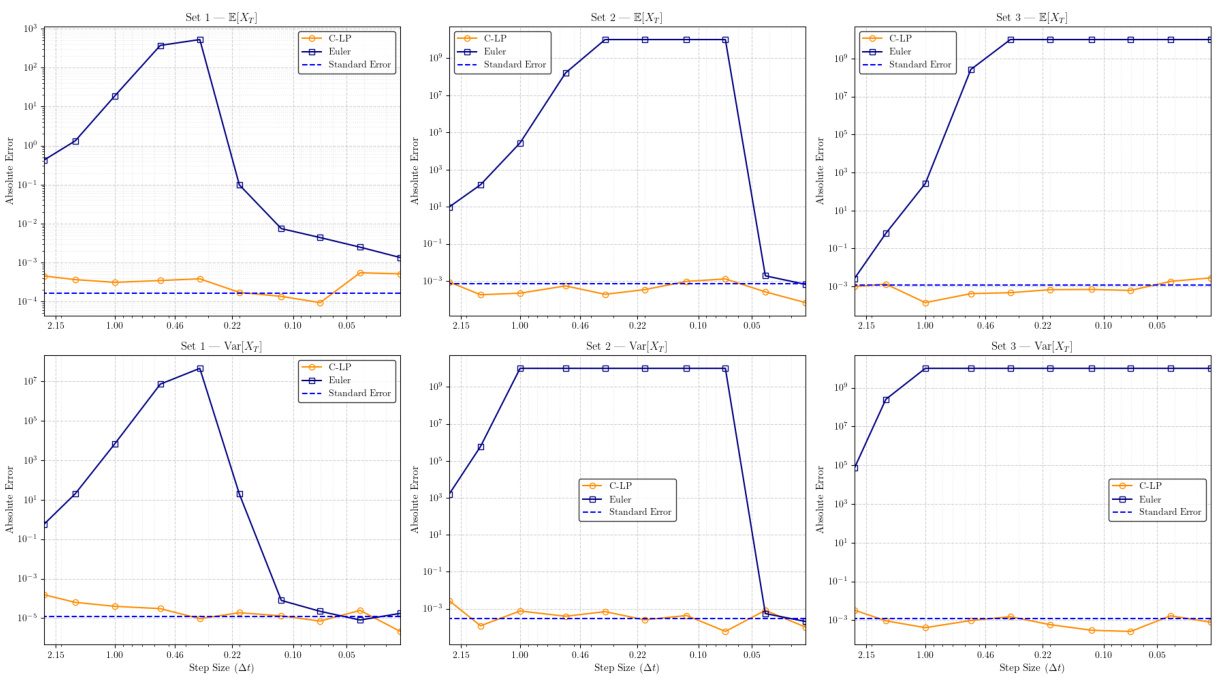
3.3. 图3（C-LP与Euler收敛对比）[page::18]

• 描述: 不同参数设定与步长下，比较C-LP法和Euler法对积分方差期望和方差的绝对误差。横轴为时间步长$\Delta t$，纵轴绝对误差。

- 解读: C-LP法即使步长较大$\Delta t \approx 2.15$时，误差依旧低于Euler $\Delta t < 0.1$的水平。表明C-LP适合大步长情况，显著节省计算资源。

• 意义: 该数值实验强力验证了新方法在不同模型参数环境下的高效性及准确性。

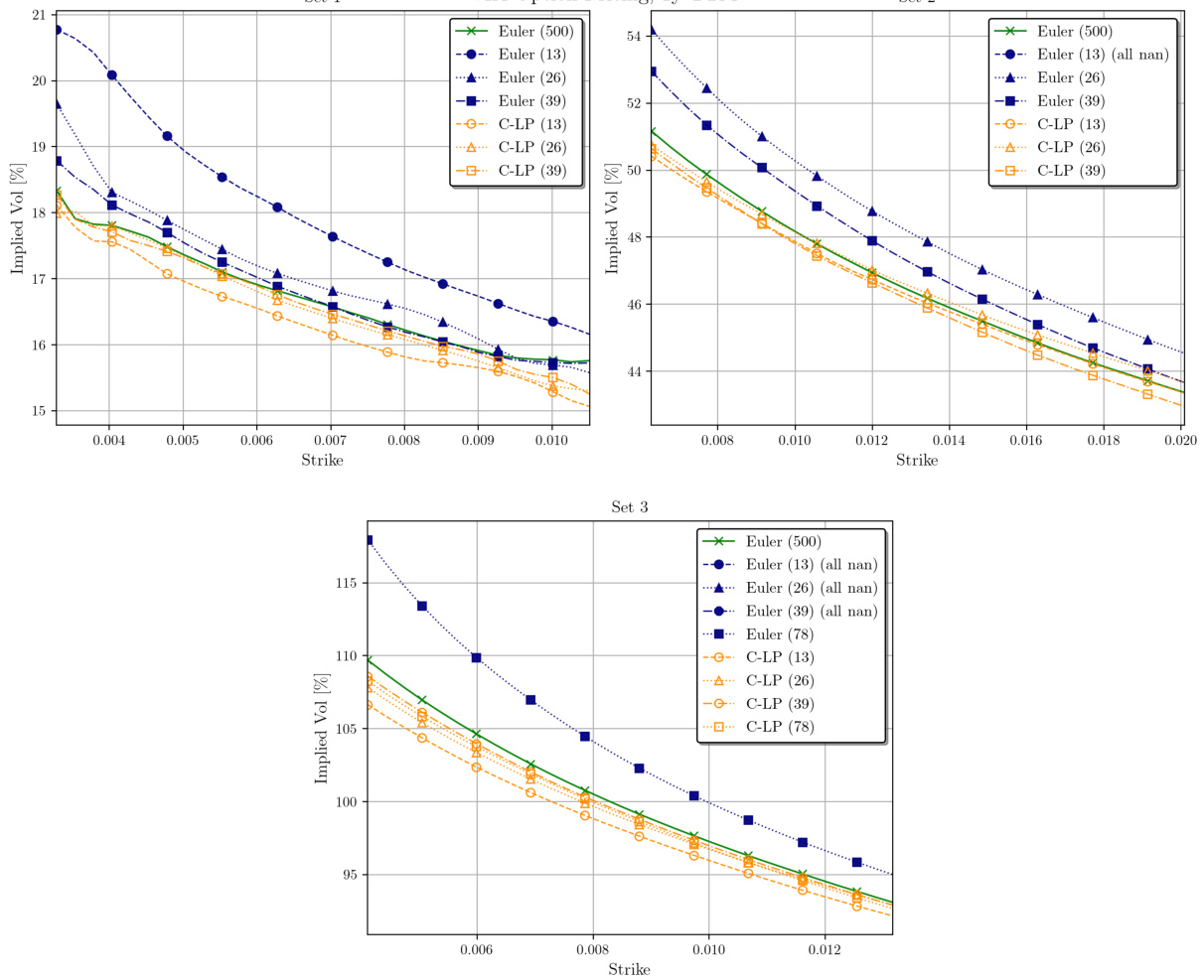
3.4. 图4（VIX期权定价）[page::19]

• 描述: 模拟欧式VIX期权隐含波动率，用不同离散步长的C-LP和Euler方法定价。横轴为执行价，纵轴为隐含波动率。

- 解读: C-LP各步长定价结果与500步Euler近似一致，且不出现数值不稳定；低步长Euler（13、26、39步）出现较明显偏差甚至数值异常（NAN）。

• 意义: 凸显C-LP方法在实际金融衍生品定价中的应用价值，尤其风险较高或计算资源有限时。

3.5. 图5（C-LP与Abi/Attal线性估计对比）[page::20]

• 描述: 显示C-LP法与Abi/Attal方法计算的线性拟合与EM法样本散点的对比。两图不同参数设置。

- 解读: C-LP的线性拟合更紧密贴合散点，Abi/Attal方案存在明显偏离，尤其在某些参数下系统误差更大。

• 意义: 该对比支持文中关于C-LP为最佳$L^2$投影的理论论断，提升了数值效果。

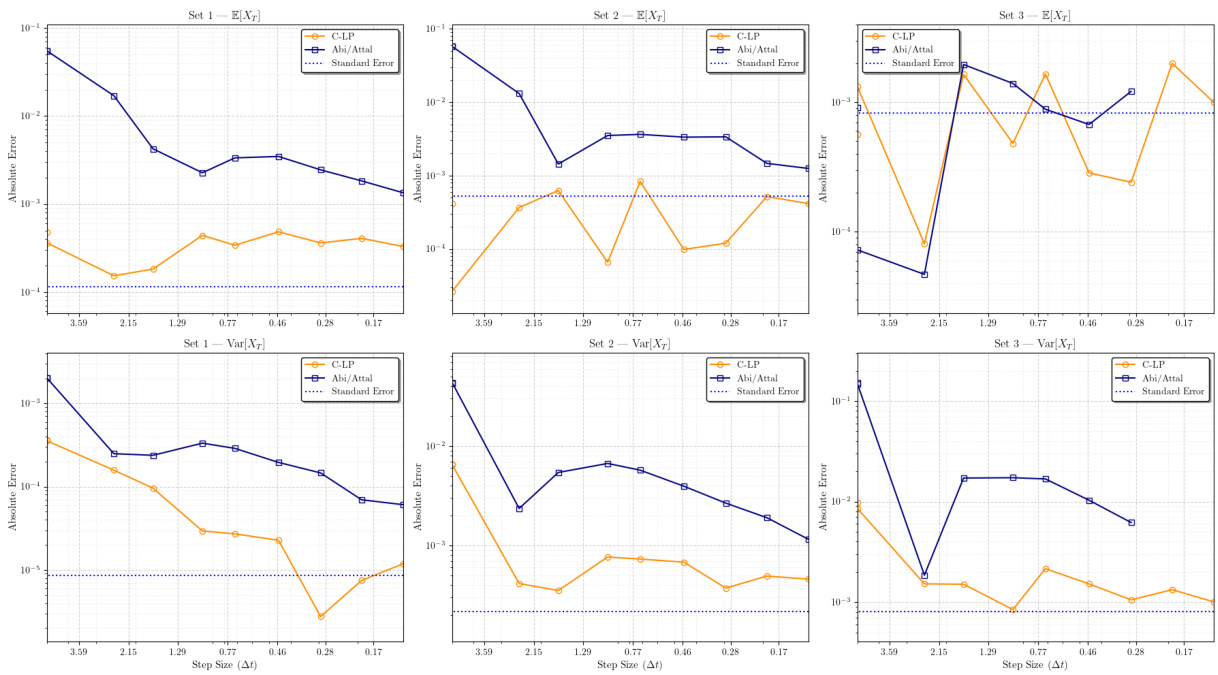
3.6. 图6（收敛性对比）[page::20]

• 描述: 比较C-LP与Abi/Attal方案在积分方差期望和方差绝对误差上的收敛，横轴为步长$\Delta t$。

- 解读: C-LP误差显著小于Abi/Attal，尤其在较大步长时差异更大。Abi/Attal方法在参数集3下表现不稳定（误差较大或不收敛），而C-LP保持精度稳定。

• 意义: 进一步证明C-LP在准确性和鲁棒性上的优势，尤其适合模拟复杂粗糙波动率模型。

---

4. 估值分析

报告未涉及直接定价估值模型或目标价格，但针对衍生品价格中的VIX期权进行了数值实验，展示了该模拟方法对波动率期权定价的重要影响，隐含波动率的模拟结果依赖于积分方差的精确模拟[page::18-19]。

C-LP方法可以视为通过提高积分方差仿真的准确度和效率，间接提升了期权定价的稳定性和可信度。

---

5. 风险因素评估

论文未直接陈述模型风险评估，但通过引入约束条件，避免模拟过程生成负波动率，明显减少了数值异常的风险。这种约束的数学定义与证明，保证了路径的合理性和稳定性，降低了传统高维Markov过程模拟中常见的数值爆炸或失败风险[page::10-13]。

此外，较大步长模拟方法的引入缓解了传统Euler小步长数值成本过高的风险，对实际应用中计算资源有限的情况尤为重要。

---

6. 审慎视角与细微差别

• 假设依赖: 本方法建立在$L^2$空间中线性投影的假设下，内部仍是对非线性复杂过程的线性近似，潜在误差依赖于非线性成分的大小，具体表现为逆高斯分布的二阶矩拟合误差。

- 参数敏感性: 实验显示部分参数（如vol-of-vol $\nu$，初始波动率$v0$）对误差影响显著，需要在实际应用中注意参数稳定性和估计精度。

• 局限性: 未提供对极端市场条件（如跳跃或大幅波动）的模拟适用性验证，且未明确分析多资产、跨产品一致性等问题。

- 数值复杂度: 虽然通过分解线性系统及数值积分实现效率，但对于极大$N$和高频策略，数值开销仍未量化，可能存在提升空间。

---

7. 结论性综合

本报告系统阐释了Lifted Heston模型中基于积分方差隐式采样的最新模拟算法——约束线性投影法（C-LP）。该方法通过在$L^2$意义下寻找积分方差与驱动扩散量的最佳线性关系，将积分方差采样还原为逆高斯分布的首达时间采样问题，实现了理论上最优的线性近似和采样效率。另一方面引入明确的约束机制，保证数值模拟波动率非负，确保了算法的稳定性和适用性。

从具体层面来看，该方案克服了传统Euler方法小步长限制和粗糙波动率模型的非马尔可夫结构带来的挑战，提供了可以使用大步长但不损失精度的模拟工具，极大节省了计算量。这一方法特别适用于含有粗糙波动特征的Lifted Heston模型，且在实际金融产品如VIX期权定价中表现出较好的应用价值。

通过详细的矩阵分析和数值验证，报告展示了C-LP方法对积分方差的期望和方差具有弱收敛性，且在多个参数集上相较于Euler模拟和Abi/Attal方法均表现出更优的数值性能和稳定性。此外，辅助的图表生动展示了线性近似的准确性、约束的重要作用、及实际模拟过程中误差随步长变化的规律，为理解整套方法提供了清晰的视觉和量化证明。

综上，作者提出的C-LP积分方差隐式采样方案是目前关于Lifted Heston模型蒙特卡洛模拟的最优方案之一，具备理论支持、数值优势和实际应用潜力，是强有力的金融工程工具，对进一步研究复杂波动率结构及相关衍生品定价具有重要意义[page::全部]。

---

附：关键图表示意

• 图1：积分方差与扩散过程的最佳线性拟合，展示拟合效果及残差结构。

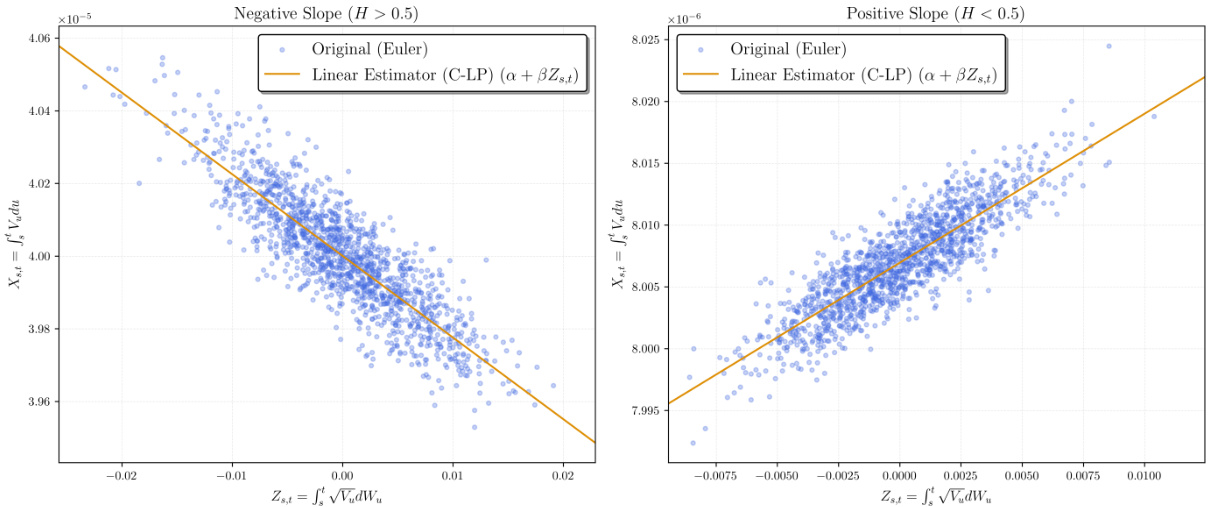
• 图2：未约束与约束线性斜率对波动率路径影响，表明约束避免负值。

• 图3：C-LP与Euler方法收敛特性对比，C-LP支持更大步长且误差低。

• 图4：VIX期权隐含波动率定价精度对比，C-LP模拟优于Euler。

• 图5：不同线性拟合方案与EM模拟对比，C-LP拟合更贴近真实。

• 图6：积分方差期望及方差绝对误差收敛曲线，C-LP误差普遍低于Abi/Attal。

---

### 备注：以上内容均依托于文献给出的理论证明、数值实验和引用的图表数据，结构和数字均对应报告原文页码。

报告