Computing the SSR
创建于 更新于
摘要
本报告围绕偏度粘滞比(SSR)的理论构建与计算展开,提出了基于特征函数的无模型表达式,推广了SSR的短期极限为波动率过程Hurst指数加3/2,深入分析了仿射远期方差模型中的解析形式及路径依赖特征。通过森林展开方法推导出SSR的高阶近似,并结合经典Heston和Rough Heston模型进行了数值验证,结果显示SSR对模型动态极为敏感,难以从隐含波动率表面直接推断,实证观察的SSR值与主流粗波动率模型存在显著差异,这一不一致性仍是重要研究课题[page::0][page::1][page::5][page::7][page::8][page::9][page::14][page::16][page::17].
速读内容
- 偏度粘滞比(SSR)定义及计算框架简介 [page::0][page::1]
- SSR定义为ATM波动率变化对标的价格变化的回归系数与ATM波动率斜率的比值。
- SSR对于期权做市商在对冲隐含波动率和价格风险时至关重要。
- SSR与特征函数的联系与无模型表达式 [page::3][page::4]
- SSR可用期权价格对应的特征函数表示,通过积分公式给出表达式,适用于广泛模型。
- 仿射远期方差(AFV)模型中SSR的显式计算公式 [page::4][page::5]
- 利用卷积Riccati方程的解构造特征函数,SSR公式简化为显式积分形式。
- 经典Heston模型为AFV模型特例,SSR数值积分计算可行。
- SSR的森林展开方法及短期行为分析 [page::6][page::7][page::8][page::9]
- 采用diamonds产品树的森林展开,对特征函数进行展开导出SSR高阶近似。
- SSR短期极限为波动率Hurst指数H加3/2,验证了相关文献中对局部与隐含波动率斜率关系的推断。
- 具体量化模型及参数下的SSR数值比较 [page::12][page::14][page::15]
- 经典Heston和Rough Heston模型(不同H值)SSR数值计算,森林展开与仿射积分公式吻合。
- SSR对远期方差曲线形状极为敏感,不同Contango和Backwardation情形下SSR表现差异明显。


- SSR对模型动态参数的敏感性与实证不一致问题 [page::16][page::17][page::18]
- 三组参数生成近乎相同的隐含波动率曲面,但对应SSR曲线差异显著,说明SSR动态敏感,无法单凭隐含波动率表面推断。
- 实测SSR通常为1.0~1.3,主流粗波动率模型预测值普遍偏高,短期内Hurst参数取较小值可获得相对合理SSR。


- SSR定义中的离散效应微弱,不足以解释观测与模型值差异 [page::20][page::21]
- 分析了有限时间窗口$\Delta$对回归系数$\beta^\Delta_t(T)$的影响,误差一般不超过2.5%。
- 量化策略总结: 无明确量化策略回测,但详细展开了SSR计算的数学框架和数值方法,涵盖森林展开及参数敏感性分析[page::5][page::7][page::9][page::12][page::14][page::16].
深度阅读
详细分析报告:《Computing the SSR》
作者:Peter K. Friz (TU and WIAS Berlin) 与 Jim Gatheral (Baruch College, CUNY)
日期:2024年6月25日
---
1. 元数据与概览
- 标题:Computing the SSR
- 作者及机构:Peter K. Friz(TU和WIAS Berlin),Jim Gatheral(Baruch College, CUNY)
- 发布日期:2024年6月25日
- 主题:深入计算和理解“Skew-Stickiness Ratio”(SSR),一种期权隐含波动率曲面变动中的关键量,对市场做市商和期权交易者极为重要。
- 报告概要:本文提出了一个无模型依赖的(model-free)SSR表达式,基于特征函数,扩展SSR的认识至随机波动率背景。关键结论包括SSR的短期期限极限与波动率过程的Hurst指数\(H\)关系,即SSR短期期限为\(H+3/2\)(以前已知扩散情况为2,是该结论的特例)。论文还针对仿射远期方差(AFV)模型进行了特化,并用传统与粗糙Heston模型具体示例演示计算方法。报告强调SSR不仅依赖波动率水平,还显著取决于远期方差曲线形状与路径依赖性,对风险管理和定价策略有重要影响。
- 报告意图:为金融实务提供更精确的SSR计算工具,揭示SSR对模型结构和动态的敏感性,探讨短期极限行为及路径依赖带来的影响,指出现有粗糙波动率模型与市场实际观测SSR的明显差异及其潜在原因。
---
2. 逐节深度解读
2.1 引言与SSR定义(第0-1页)
- 关键点:定义了欧式期权隐含波动率\(\sigma{\mathrm{BS,t}}(k,T)\),其中\(k=\log(K/St)\)为对数行权价,点明以BS模型价差公式匹配期权市价的隐含波动率即为“BS隐含波动率”。
- SSR概念:市场做市商对期权进行对冲时,除了直接对冲现货变动,还要对冲隐含波动率对现货变动的响应,即通过回归估计 \(\betat(T) = \frac{\mathbb{E}[\delta\sigma{t}(T)|\delta St]}{\delta Xt}\),再用速率斜率 \(St(T)=\left.\partialk\sigma{\mathrm{BS,t}}(k,T)\right|{k=0}\) 定义SSR为
\[
\mathscr{R}t(T) = \frac{\betat(T)}{St(T)}.
\]
SSR衡量隐含波动率斜率随现货变动的改变程度,是理解隐含波动率微观动态的核心量。
2.2 SSR在随机波动率模型下的表达(第2页)
- SSR表达:SSR回归系数可表述为波动率与对数价格的协方差变化率比值,应用伊藤公式转为偏微分算子形式,写为
\[
\betat(T) = \rho Dt^\xi \sigmat(T), \quad Dt^\xi := \frac{1}{\sqrt{Vt}} \intt^T du\,ft(\xi)\kappa(u-t) \frac{\delta}{\delta \xit(u)}.
\]
这里引入的算符\(Dt^\xi\)体现了远期方差曲线对隐含波动率的功能梯度影响,关键地捕捉了SSR对远期方差变化的敏感度。
2.3 SSR与特征函数的联系(第3-4页)
\[
\mathcal{R}t(T) = -\frac{
\int0^\infty \frac{da}{a^2 + 1/4} \Re \left[ \rho Dt^\xi \psit(T; a - i/2) e^{\psit(T; a - i/2)} \right]
}{
\int0^\infty \frac{a\, da}{a^2 + 1/4} \Im \left[ e^{\psit(T; a - i/2)} \right]
},
\]
其中\(\psi = \log \varphi\)为特征函数的对数,即累积生成函数(CGF)。该表达为报告的核心无模型结果,连接了期权定价的特征函数表示与SSR这一隐含波动率微观动态指标。
2.4 AFV模型中的SSR计算(第4-5页)
\[
\mathcal{R}t(T) = -\frac{
\int0^\infty \frac{da}{a^2 + 1/4} \Re \left[ \rho (\kappa \star g)(T-t; a - i/2) e^{\intt^T \xit(s) g(T-s; a - i/2) ds} \right]
}{
\int0^\infty \frac{a\, da}{a^2 + 1/4} \Im \left[ e^{\intt^T \xit(s) g(T-s; a - i/2) ds} \right]
}.
\]
2.5 森林展开法计算SSR(第6-11页)
\[
\lim{T\to t} \mathcal{R}t(T) = \alpha + 1,
\]
其中\(\alpha\approx H + 1/2\),对应Hurst指数的函数。
2.6 SSR对远期方差曲线形状和路径的敏感性(第14-16页)
\[
\mathcal{R}t(T) \approx \frac{
\left( \intt^T \xit(s) ds \right) \intt^T \sqrt{Vt} ft(\xi) \kappa(u-t) du
}{
Vt \intt^T ds \ints^T \mathbb{E}t[ \sqrt{Vs} fs(\xi)] \kappa(u-s) du
}.
\]
2.7 SSR对模型参数动态的敏感性(第16-18页)
---
3. 图表深度解读
图5.1(第14页)
- 两种计算方法对不同\(H\)值在极短到较长期限均表现一致性,确认森林展开的有效性。
- 对小\(H\)(如0.05或0.1)时,短期一致性持续时间很短,提示粗糙模型短期SSR表现更为复杂。
- SSR值整体随\(H\)增大而升高,符合理论短期极限\(H+3/2\)规则。
图6.1(第15页)
- 解读:
- Contango曲线(橙色)导致SSR明显抬高,Backwardation(粉色)则降低SSR,相较平坦曲线(绿色)。
- 右图展示了远期方差曲线差别,验证左图SSR对远期曲线的敏感响应。
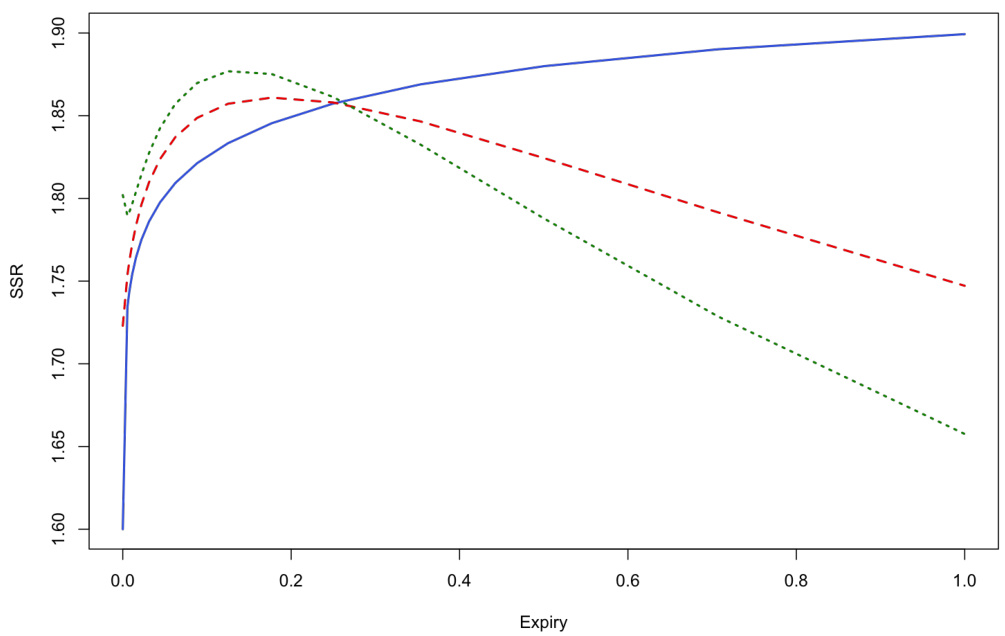
图7.1与图7.2(第17-18页)
- 图7.2:对应三组参数的SSR曲线明显区分,体现SSR对不同参数组合(动态结构)敏感。
---
4. 估值分析
本报告不是标准意义上的估值报告,不涉及股票价格或期权具体目标价格的推荐或评估,而是围绕SSR这一波动率动态指标进行理论计算和数值分析。
报告在第4节利用仿射远期方差模型中卷积黎卡提方程形式,对SSR的表达式进行了具体化处理。
- 利用特征函数表达式和Lewis积分公式计算期权价格,基于期权价格的敏感度分析提取SSR。
- 通过森林展开法,对特征函数CGF展开为多项式森林,从而实现渐近式估算,揭示SSR短期极限和依赖关系。
- 数值积分和已知闭式函数(如Heston模型中的C,D函数)实现SSR的实际计算。
---
5. 风险因素评估
- 模型不确定性风险:报告指出实际市场观察的SSR范围(1.0至1.3)往往低于常用粗糙模型预测,存在实证与理论不一致风险,提示当前模型可能不足以完全捕获市场动态。
- 离散观测效果:报告附录A证明,在实际非连续数据情况下,SSR的离散估计误差仅在约2.5%以内,不足以解释主要不一致问题。
---
6. 审慎视角与细微差别
- 假设隐含细节:SSR公式的推导依赖于远期方差可微性及某些高级平稳性假设,粗糙模型近似和森林展开在实际较短期限内适用性有限。
- 对市场实际的挑战:SSR的市场观测值常显著低于仿射及粗糙模型计算值,存在潜在模型遗漏或实际市场行为更复杂的可能性,报告作者明确指出这是内幕学术问题,需进一步研究。
---
7. 结论性综合
本文对Skew-Stickiness Ratio (SSR)的计算和本质进行了全面且深入的分析:
- 提出了一个基于特征函数的无模型SSR计算公式,使得SSR不再仅限于特定模型,具有广泛适用性。
- 特别在仿射远期方差模型框架下,SSR可以通过卷积黎卡提方程求解函数明确表达,实现数值计算。
- 通过“森林展开”理论分析,明确了SSR短期极限表现依赖于波动率过程的Hurst指数,验证并拓展了前人相关猜想,为粗糙波动率模型中的动态行为提供了坚实数学基础。
- 数值计算和模拟结果表明,SSR不仅受波动率水平影响,更对远期方差曲线形态和股票历史路径极为敏感,体现路径依赖性。
- 经典Heston与粗糙Heston模型的具体示例说明SSR的计算方法极其灵活,但粗糙模型的SSR预测与市场观测存在偏差,尤其在实务中观察到的SSR普遍较小。
- SSR作为对隐含波动率微观动态的补充诊断工具,不可单纯从隐含波动率表面推出,揭示了模型辨识和市场动态的复杂性。
- 附录分析显示实际估计中时间粒度引起的离散误差很小,不足以解释理论与实际差异,提示需进一步探索其他市场机制或模型假设。
总体而言,作者通过理论推导结合数值实证,不仅丰富了金融衍生品微观动态理论框架,也展示了SSR这一关键指标在风险管理和模型校准中的潜力与挑战。未来研究可聚焦于SSR在更一般化随机波动模型下的表现,及其与市场数据的匹配问题。
---
8. 图表展示(典型图例)
图5.1:粗糙Heston模型SSR与Hurst指数对比
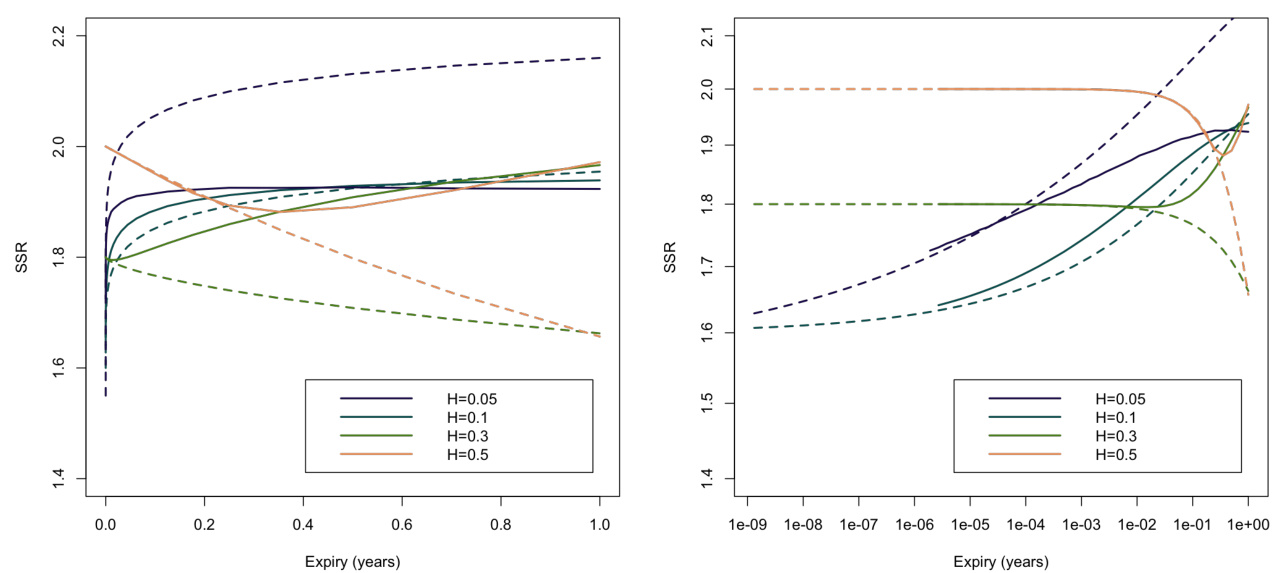
图6.1:不同远期方差曲线形态导致的SSR差异
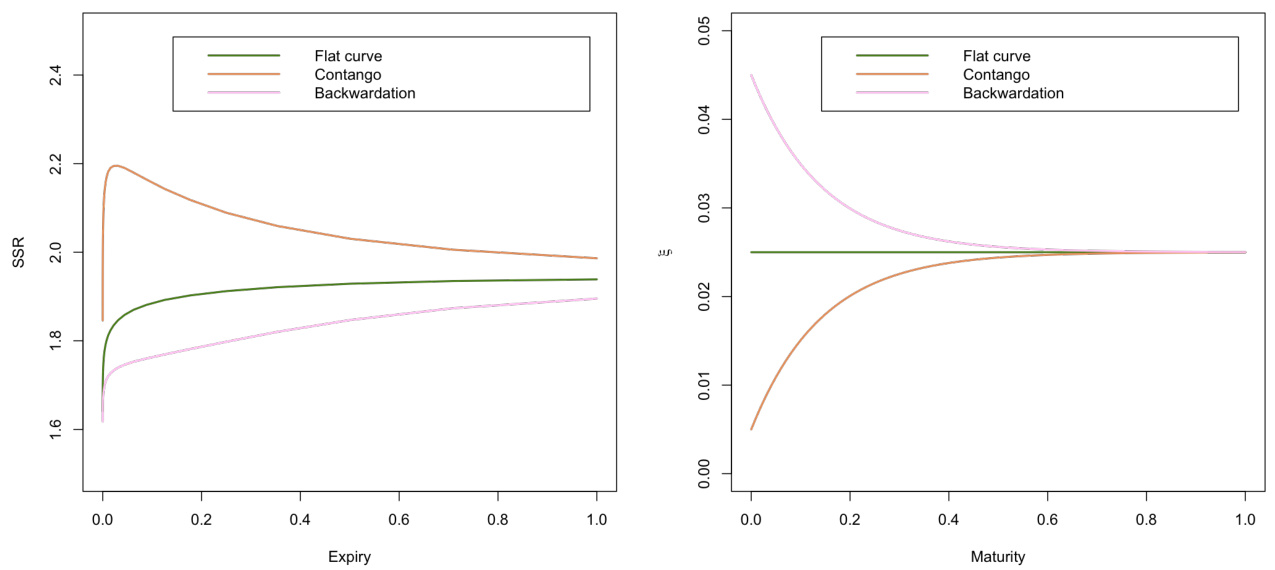
图7.1:不同参数集合下的隐含波动率笑脸近似重合
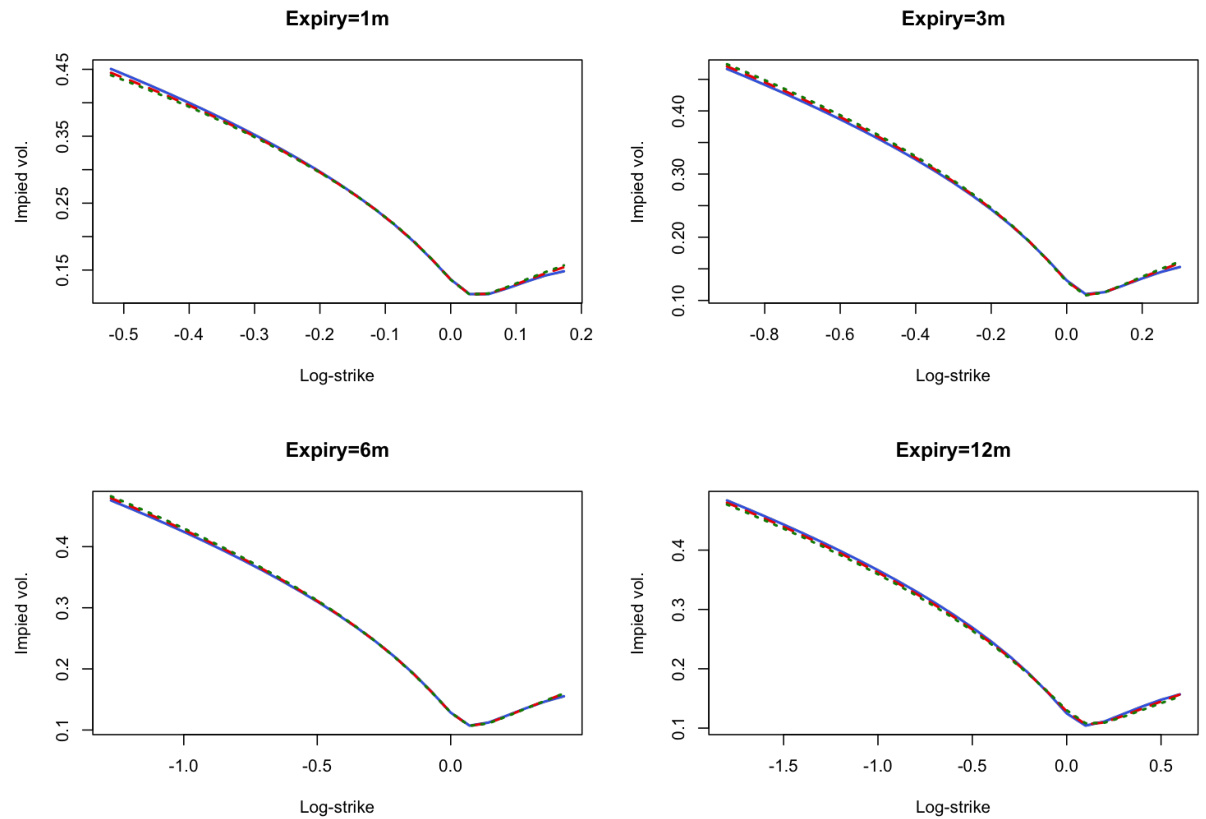
图7.2:对应参数集的SSR曲线明显区分
---
参考文献
完整、详尽的文献引用覆盖了从期权理论基础、隐含波动率动力学,到粗糙波动率模型和森林展开理论的关键文献,体现该报告立足现代金融数学前沿。
---
总结
本报告汇聚了现代金融数学关于隐含波动率动态与隐含波动率曲面变动微观结构的顶级研究成果,系统建立了一套SSR计算理论与数值方法,从无模型表达到渐近分析,再到路径依赖与实际敏感性,层层递进,为市场做市商、衍生品风险控制和模型校准提供了强有力理论支持和实践工具。报告指出的SSR与现实市场的偏差问题展示了未来研究及模型改进的重要方向。




